树状数组中查询和修改有点和区间的区别：

 常用的分为三种：

1.                 单点修改，区间查询
2.                 区间修改，单点查询
3.                 区间修改，区间查询

单点修改，区间查询：

• 将某一个数加上 x

• 求出某区间每一个数的和

   先给出基本代码

//单点修改
void add2(int x, int k) {
     while(x <= n) {
         t1[x] += k;
         x += lowbit(x);
     }
 }
区间查询
LL get_sum(int k){
     int res = 0;
      while(k) {
            res += t1[k];
            k -= lowbit(k);
        }
       return res;
}

单点修改是对一个点的数值进行修改，但是t1树状数组中的每个元素的值存的是前缀和，

当对这个单点进行修改，就要对树状数组中包含这个点的元素进行修改；

而单点修改的区间查询[l, r]的区间值表示为get_sum(r) - getsum(l - 1);

下面给出相关题目及代码 相关题目：P3374 【模板】树状数组 1 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <bits/stdc++.h>
#define lowbit(x) ((x) & (-x))
#define int long long
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll c[N];
ll n, m;
ll getsum(ll k) {
  int ret = 0;
  while (k) {
    ret += c[k];
    k -= lowbit(k);
  }
  return ret;
}
void add(ll k, ll v) {
  while (k <= n) {
    c[k] += v;
    k += lowbit(k);
  }
}

void solve()
{
    cin >> n >> m;
    vector<int> a(n + 1);
    for(int i = 1; i <= n; ++ i) {
        cin >> a[i];
        add(i, a[i]);
    }
    while(m --) {
        int op; cin >> op;
        if(op == 1) {
            int x, k; cin >> x >> k;
            add(x, k);
        } else {
            int l, r; cin >> l >> r;
            cout << getsum(r) - getsum(l - 1) << '\n';
        }
    }
}


signed main()
{
    cin.tie(nullptr) -> ios::sync_with_stdio(false) ;
    int t = 1;
    //cin >> t;
    while(t --) solve();
    return 0;
}

区间修改，单点查询

1. 将某区间每一个数加上 x；

2. 求出某一个数的值。

树状数组中怎么修改区间的值呢？和前缀和的思维一样，我们运用差分的思想 

将区间[l, r]的每一个元素都加上k， 运用差分的思想相当于add(l, k), add(r + 1, -k)。

而求出某个数的值则转化为这个数原始的值加上这个数的变化。

下面给出相关题目及代码 相关题目：P3368 【模板】树状数组 2 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <bits/stdc++.h>
#define lowbit(x) ((x) & (-x))
#define int long long
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll c[N];
ll n, m;
ll getsum(ll k) {
  int ret = 0;
  while (k) {
    ret += c[k];
    k -= lowbit(k);
  }
  return ret;
}
void add(ll k, ll v) {
  while (k <= n) {
    c[k] += v;
    k += lowbit(k);
  }
}

void solve()
{
    cin >> n >> m;
    vector<int> a(n + 1);
    for(int i = 1; i <= n; ++ i) {
        cin >> a[i];
    }
    while(m --) {
        int op; cin >> op;
        if(op == 1) {
            int l, r, x; cin >> l >> r >> x;
            add(l, x), add(r + 1, -x);
        } else {
            int x; cin >> x;
            cout << a[x] +  getsum(x) << '\n'; // 此时的树状数组维护的是差分数组
        }
    }
}


signed main()
{
    cin.tie(nullptr) -> ios::sync_with_stdio(false) ;
    int t = 1;
    //cin >> t;
    while(t --) solve();
    return 0;
}

区间修改，区间查询 ：

1. 将某区间每一个数加上 𝑘k。
2. 求出某区间每一个数的和。

区间修改同上面一样运用差分的思想，运用差分树状数组表示的是差分数组，如何用差分数组进行区间查询呢？我们推导一下即可

我们可以用两个树状数组分别维护 和两个差分数组

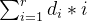
而区间查询则可用两个树状数组进行查询

下面给出相关题目及代码 相关题目：P3372 【模板】线段树 1 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <bits/stdc++.h>
#define lowbit(x) ((x) & (-x))
#define int long long
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
ll t1[N], t2[N];
ll n, m;
ll getsum(ll *t, ll k) {
  int ret = 0;
  while (k) {
    ret += t[k];
    k -= lowbit(k);
  }
  return ret;
}
void add(ll k, ll v) {
  int v1 = k * v;
  while (k <= n) {
    t1[k] += v, t2[k] += v1;
    k += lowbit(k);
  }
}
void add1(int l, int r, ll v) {
  add(l, v), add(r + 1, -v);
}

long long getsum1(int l, int r) {
  return (r + 1ll) * getsum(t1, r) - 1ll * l * getsum(t1, l - 1) -
         (getsum(t2, r) - getsum(t2, l - 1));
}

void solve()
{
    cin >> n >> m;
    ll old = 0, a;

    for(int i = 1; i <= n; ++ i) {
        cin >> a;
        add1(i, i, a);
    }

    while(m --) {
        ll q, l, r, d;
        cin >> q;
        if(q == 1) {
            cin >> l >> r >> d;
            add1(l, r, d);
        } else {
            cin >> l >> r;
            ll ans = getsum1(l, r);
            cout << ans << '\n'; 
        }
    }
}


signed main()
{
    cin.tie(nullptr) -> ios::sync_with_stdio(false) ;
    int t = 1;
    //cin >> t;
    while(t --) solve();
    return 0;
}