目录
实验题目
实验题目: 对快速排序、大根堆排序,两种排序方法进行比较,写出大根堆排序算法。并对它们最坏、最好,平均情况进行比较分析。并列举一个实例,上机验证说明。
实验说明:
快速排序算法如下:
问题分析
快速排序
快速排序(QuickSort)是一种高效的、基于分治法的排序算法,由C. A. R. Hoare在1960年提出。它的工作原理是通过选择一个“枢轴”元素,将数组分为两个子数组,使得左边的子数组中的所有元素都小于或等于枢轴,右边的子数组中的所有元素都大于枢轴,然后递归地对这两个子数组进行同样的操作,直到整个数组有序。
1.选择枢轴:从数组中选择一个元素作为枢轴(pivot),一般是数组中的第一个元素。
2.分区操作:重新排列数组,使得所有比枢轴小的元素放在其左侧,所有比枢轴大的元素放在其右侧。这个过程称为分区(partitioning)。经过这一步骤后,枢轴就位于其最终的位置上。
3.递归调用:对枢轴左右两侧的子数组分别递归调用快速排序算法,直到每个子数组的大小为1或0,即已经有序。
4.合并结果:由于每次分区后枢轴已经位于正确的位置,且递归调用会对左右子数组进行排序,因此不需要额外的合并步骤,整个数组自然就变得有序了。
具体的过程为:先将数组的第一个元素作为pivot,然后使得low指针指向数组中的第一个元素,hight指向数组中的最后一个元素,然后看hight指向的元素,如果小于pivot则与hight指向的元素交换,否则继续向左移动,如果元素发生了交换,就让low指针再向右移动比较指向的值与pivot的大小,如果更大,就与hight指向的元素交换位置,否则继续向右移动。
如此往复,直到low与hight指针指向同一个位置,最后将pivot放入这个位置。
以pivot为分隔,将数组分隔为左右两个部分,再以此规则,依次对左右两边进行操作,直到最终数组有序。
int part(int* r, int low, int hight) //划分函数
{
int i = low, j = hight, pivot = r[low]; //基准元素
while (i < j)
{
while (i < j && r[j] > pivot) //从右向左开始找一个 小于等于 pivot的数值
{
j--;
}
if (i < j)
{
swap(r[i++], r[j]); //r[i]和r[j]交换后 i 向右移动一位
}
while (i < j && r[i] <= pivot) //从左向右开始找一个 大于 pivot的数值
{
i++;
}
if (i < j)
{
swap(r[i], r[j--]); //r[i]和r[j]交换后 i 向左移动一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
}
//快速排序
void Quicksort(int* r, int low, int hight)
{
int mid;
if (low < hight)
{
mid = part(r, low, hight); // 返回基准元素位置
Quicksort(r, low, mid - 1); // 左区间递归快速排序
Quicksort(r, mid+1, hight); // 右区间递归快速排序
}
}大根堆排序
大根堆排序(HeapSort)是一种基于二叉堆数据结构的比较排序算法。它利用了最大堆(Max-Heap)或最小堆(Min-Heap)的特性来对数组进行排序。在大根堆排序中,我们使用的是最大堆,其中每个节点的值都大于或等于其子节点的值。通过构建和调整最大堆,可以有效地将元素按降序排列。
1.构建最大堆:将输入数组构建成一个最大堆。这一步骤称为“堆化”(heapify)。对于一个给定的数组,可以通过从最后一个非叶子节点开始,逐层向上调整每个节点的位置,确保满足最大堆的性质。
大根堆的建立其实就是调用多次大根堆的调整。
void BuildMaxHeap(int A[],int size){
/*
对A中任意结点i的父结点为(i-1)/2,对于最后一个元素的父结点
为(size-1-1)/2 = (size-2)/2.
*/
for(int i = (size - 2) / 2; i >= 0; i--)
AdjustDown(A,size,i);
}2.交换与重新堆化:一旦构建好了最大堆,堆顶元素就是当前数组中的最大值。将其与数组末尾的元素交换位置,然后减少堆的大小(即不再考虑最后一个元素),从而将最大值固定在数组的正确位置。接下来,对剩余的未排序部分再次进行堆化操作,以确保新的堆顶元素是剩余元素中的最大值。重复这个过程,直到整个数组都被排序。
void AdjustDown(int A[],int size,int k){
int p = k;//p执行当前结点
int i = 2 * p + 1;//使i始终指向p的较大子结点
while(i < size){
/*使i指向较大的兄弟*/
if(i < size-1 && A[i] < A[i+1])
i++; //i<size-1保证i有右兄弟
if(A[p] >= A[i])
break;//如果父结点p大于等于较大子结点i,那么不需求调整
else{
swap(A[p],A[i]);
p = i;
i = 2*p + 1;
}
}
}3.结果:经过上述步骤后,原始数组已经被排序成升序排列。如果需要降序排列,则可以在构建最小堆的基础上执行类似的操作。
具体的过程为:先调整当前的数组为一个大根堆,从最大的非叶子结点开始调整一直到根结点,调整的规则为,将子节点中的最大元素与父节点交换,如果父结点大于子节点中的最大值则说明此时已经是大根堆,不用调整,这样调整到根节点,就构造了一个大根堆。
再将根节点与最大的叶子结点交换位置(此时已经找到这个数组的最大值,将这个值放在序号最大的位置)然后再调整这个新的根结点,然后再按照上述的规则调整为一个大根堆,将此时的最大值(也就是整个数组第二大的值)与此时序号最大的叶子结点交换(此时序号最大的叶子结点的序号为最大序号减一),如此往复就排序好了一个从左到右,由小变大的有序数组。
void AdjustDown(int A[],int size,int k){
int p = k;//p执行当前结点
int i = 2 * p + 1;//使i始终指向p的较大子结点
while(i < size){
/*使i指向较大的兄弟*/
if(i < size-1 && A[i] < A[i+1])
i++; //i<size-1保证i有右兄弟
if(A[p] >= A[i])
break;//如果父结点p大于等于较大子结点i,那么不需求调整
else{
swap(A[p],A[i]);
p = i;
i = 2*p + 1;
}
}
}
void BuildMaxHeap(int A[],int size){
/*
对A中任意结点i的父结点为(i-1)/2,对于最后一个元素的父结点
为(size-1-1)/2 = (size-2)/2.
*/
for(int i = (size - 2) / 2; i >= 0; i--)
AdjustDown(A,size,i);
}
void HeapSort(int A[],int size){
//先建立大根堆
BuildMaxHeap(A,size);
for(int i = size; i > 1; i--){//i表示每次调整时数组的大小
swap(A[0],A[i-1]);
AdjustDown(A,i - 1,0);
}
}
int part(int* r, int low, int hight) //划分函数
{
int i = low, j = hight, pivot = r[low]; //基准元素
while (i < j)
{
while (i < j && r[j] > pivot) //从右向左开始找一个 小于等于 pivot的数值
{
j--;
}
if (i < j)
{
swap(r[i++], r[j]); //r[i]和r[j]交换后 i 向右移动一位
}
while (i < j && r[i] <= pivot) //从左向右开始找一个 大于 pivot的数值
{
i++;
}
if (i < j)
{
swap(r[i], r[j--]); //r[i]和r[j]交换后 i 向左移动一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
}两种排序方法时间复杂度的比较
快速排序
平均时间复杂度:O(n log n) 在平均情况下,快速排序通过分治法将数组分成两部分,并递归地对这两部分进行排序。这种分治策略使得其平均时间复杂度为O(n log n)。
最坏时间复杂度:O(n²) 当每次选择的枢轴(pivot)都是最大或最小元素时,快速排序会退化为最坏情况。例如,当数组已经有序,而每次选择的枢轴都是数组的第一个或最后一个元素时,会导致每次划分都极不平衡,从而时间复杂度变为O(n²)。
最好时间复杂度:O(n log n) 在理想情况下,每次选择的枢轴都能将数组均匀分成两半,这样递归的深度为log n,每层递归处理n个元素,因此时间复杂度为O(n log n)。
大根堆排序
大根堆排序无论输入数据如何分布,都能保证O(n log n)的时间复杂度。这是因为堆排序依赖于最大堆这种数据结构的特性,构建最大堆的时间复杂度为O(n),随后每次删除最大元素并重新调整堆的操作需要O(log n),总共进行n次这样的操作。
总的代码
#include <stdio.h>
#include <iostream>
#include <math.h>
#include <algorithm>
using namespace std;
void AdjustDown(int A[],int size,int k){
int p = k;//p执行当前结点
int i = 2 * p + 1;//使i始终指向p的较大子结点
while(i < size){
/*使i指向较大的兄弟*/
if(i < size-1 && A[i] < A[i+1])
i++; //i<size-1保证i有右兄弟
if(A[p] >= A[i])
break;//如果父结点p大于等于较大子结点i,那么不需求调整
else{
swap(A[p],A[i]);
p = i;
i = 2*p + 1;
}
}
}
void BuildMaxHeap(int A[],int size){
/*
对A中任意结点i的父结点为(i-1)/2,对于最后一个元素的父结点
为(size-1-1)/2 = (size-2)/2.
*/
for(int i = (size - 2) / 2; i >= 0; i--)
AdjustDown(A,size,i);
}
void HeapSort(int A[],int size){
//先建立大根堆
BuildMaxHeap(A,size);
for(int i = size; i > 1; i--){//i表示每次调整时数组的大小
swap(A[0],A[i-1]);
AdjustDown(A,i - 1,0);
}
}
int part(int* r, int low, int hight) //划分函数
{
int i = low, j = hight, pivot = r[low]; //基准元素
while (i < j)
{
while (i < j && r[j] > pivot) //从右向左开始找一个 小于等于 pivot的数值
{
j--;
}
if (i < j)
{
swap(r[i++], r[j]); //r[i]和r[j]交换后 i 向右移动一位
}
while (i < j && r[i] <= pivot) //从左向右开始找一个 大于 pivot的数值
{
i++;
}
if (i < j)
{
swap(r[i], r[j--]); //r[i]和r[j]交换后 i 向左移动一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
}
//快速排序
void Quicksort(int* r, int low, int hight)
{
int mid;
if (low < hight)
{
mid = part(r, low, hight); // 返回基准元素位置
Quicksort(r, low, mid - 1); // 左区间递归快速排序
Quicksort(r, mid+1, hight); // 右区间递归快速排序
}
}
int main()
{
//数据的输入
int a[10001];
int b[10001];
int N;
cout << "请输入要排序的数据的个数: " << endl;
cin >> N;
cout << "请输入要排序的数据: " << endl;
for (int i = 0; i < N; i++)
{
cin >> a[i];
b[i] = a[i];
}
//快速排序
Quicksort(a, 0, N - 1);
cout << "快速排序后的序列为: " << endl;
for(int i = 0; i < N; i++){
cout << a[i] << " ";
}
cout << endl;
//大根堆排序
HeapSort(b,N - 1);
cout << "大根堆排序后的序列为:" << endl;
for(int i = 0; i < N; i++) {
cout << b[i] << ' ';
}
cout << endl;
return 0;
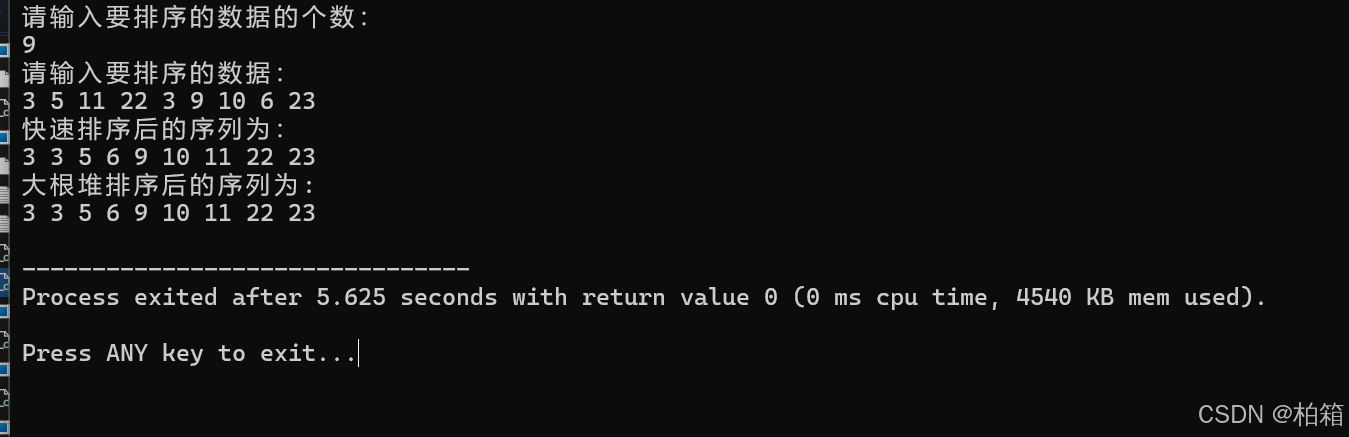
}运行结果
采用的样例为:3 5 11 22 3 9 10 6 23