对于初学者来说，递归（recursion）是一个相对难以理解并且难以应用的知识。因此在这一篇中，我将会详细讲解递归相关的知识。

递归（recursion）

假设有一个方法在编写的过程中直接或者间接地调用自身，直到达成某个条件，并且一层一层地向上返回结果，那么这个方法就使用了递归。因此，递归通常指的是在声明过程中使用了自身的方法。基于以上原理，递归的基本格式就诞生了。

public void RecursionMethod(){
        //在编写RecursionMethod的过程中使用该语句调用了RecursionMethod方法，因此称为递归
        RecursionMethod();
    }

不过，在实际应用中，使用到递归的方法通常都是需要返回值的。

编写

在熟悉了递归的定义之后，我们还需要知道递归是如何编写的。在编写的时候，通常需要设置两个条件：递归条件和结束条件。

如上文所说，使用递归的方法需要将值一层一层返回，因此让这些值一步一步返回的条件就是递归条件。最终停止返回时，也需要达成某个条件。因此，停止返回时达成的条件就是递归的结束条件。值得注意的是，在实际应用中，可能会有多个递归条件和结束条件。

基于以上内容，我们再补充一下递归的基本格式：

public int RecursionMethod(int n){
       //达到结束条件返回特定值，反之继续调用自身
        if(endCondition){
            return value;
        }
        else{
            return RecursionMethod(n);
        }
    }

到目前为止，相信大家都对递归有了最基本的认识，但是如何使用递归还是一个难题。那么接下来，我们就举一个例子。

例：计算阶乘

这是一个相对简单的例子，相信大家对阶乘都不陌生。

那么用递归来计算阶乘时，我们需要考虑这种情况下的递归条件和结束条件是什么，以及结束时应该返回的值是什么。

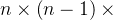
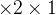
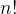
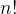
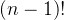
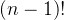
假设我们要计算整数n的阶乘，这也就意味着我们要计算…… ，这时，我们可以从另一个角度来思考问题。

在计算时，我们可以看作在计算和的乘积，因此现在我们需要计算。

而计算（n-1）时，我们又可以看作计算（n-1）和(n-2)!的乘积，以此类推，问题最终被简化成了计算……。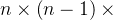

由此一来，大家就能看出来，停止循环的条件就是n=1，并且考虑到n可能为01，而0！=1，n=0也是结束条件之一。而在n=1或者n=0时，需要的返回值为1，因此，我们就可以写出以下方法：

public int factorial(int n){
        if(n==0||n==1){
            return 1;
        }
        else{
            return n* factorial(n-1);
        }
    
    }