排序
先写单趟,再写多趟,这样比较好写
排序可以理解为对商品价格的排序,对数字大小的排序,排序再生活中随处可见
冒泡排序
冒泡排序就是两个相邻的数交换,排升序,把最大的数排到最右边
时间复杂度的分析:
最坏情况:外层循环是比较的趟数N-1次,假设j 一直等于0,内层循环就每次走N次,那么时间复杂度是O(N*N)
最好情况:假设数组已经有序了,外层循环进去第一次,内层循环后一个比前一个数要大,flag 一直是0,最后只执行了一次内层循环和外层循环,就跳出外层循环了,时间复杂度:O(N)
冒泡排序的时间复杂度是:O(N*N)
外面一层循环控制趟数,里面一层循环控制一趟的比较逻辑
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//冒泡排序
//最坏:O(N^2)
//最好:O(N)->有序
void Bubblesort(int* arr, int n)
{
for (int j = 0; j < n-1; j++)
{
int flag = 0;
//一趟
for (int i = 1; i < n - j; i++)
{
if (arr[i-1] > arr[i])//防止越界
{
swap(&arr[i-1], &arr[i]);
flag = 1;
}
}
if (flag == 0)
{
break;
}
}
}
int main()
{
int arr[10] = { 2,33,41,1,2,31,331,51,1,2 };
Bubblesort(arr, 10);
for (int i = 0; i < 10; i++)
{
printf("%d ", arr[i]);
}
return 0;
}
插入排序
插入排序可以类比为抽扑克牌,先在你有三张扑克牌,分别是5,8, 9 ,摸了一张7,这张7就要插入到比前一数大,比后一个数小的位置
逻辑:假设前二个数有序,将第三个数插入到[0,1]这个区间中去
1.比所有的数都小,插入到最前面
2.比前数大,比后数小,插入到它俩中间
时间复杂度的分析:
假设最坏的情况是逆序,有n个数,将第n-1下标的数,插入到区间[0,n-2]中,这样会比较n-1次,假设每次都比较最后一次的情况是n-1次,最外层的趟数是n-1,那么时间复杂度是O(N*N)
最好的情况是顺序:每次内层循环都会break,后一项都会比前一项大,就走外层循环走了n-1次,时间复杂度是O(N)
void Insertsort(int* arr, int n)
{
//先写一趟的逻辑
// [0,end]中插入下标为end+1的数
for (int i = 0; i < n - 1; i++)
{
//一趟的过程
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (tmp < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
//放在外面为了解决,插入到最前面,end<0的情况
}
}
冒泡排序和插入排序的对比
冒泡排序和插入排序时间复杂度都是O(N^2),那么他们的效率是否相同呢?
答案是否定的,插入排序的效率比冒泡排序的效率更高
1.先说冒泡排序,冒泡最好是直接有序,但是基本上不可能,如果数字是随机数的话,冒泡基本上都是最坏的情况,冒一趟,其中一个大的数冒到后面了,但是中间可能还有其他大的数,那么基本上就是O(N^2)了
2.插入排序可能前10个数已经有序了,那么每 1 趟都只较1次,O(N)可以解决,也可能前5个数有序,都比较快,最坏的情况是逆序,但是用随机数是逆序的可能性不大
最好的情况就是比较1次,再差就是比较到中间,运气不好就是比较到最前面
希尔排序
希尔排序可以说是插入排序的变形了
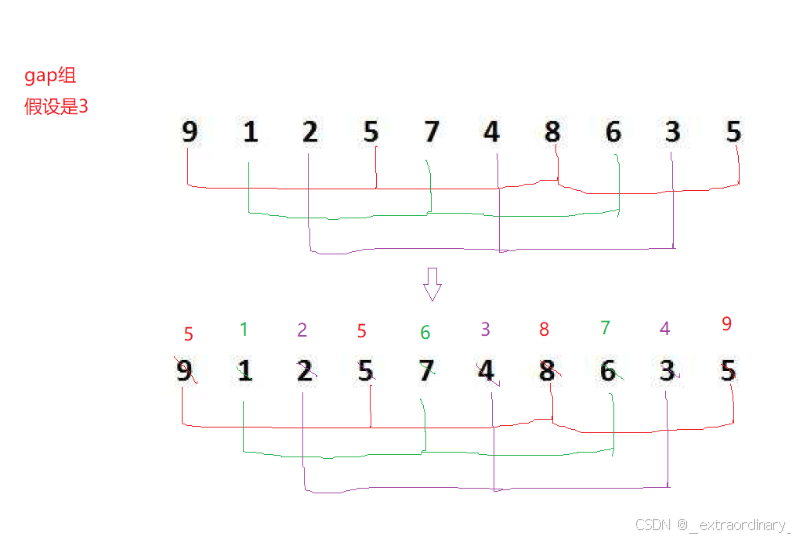
可以设置gap组排序,在gap组中分别排序,也可以在gap组中同时进行排序
希尔排序:
1.预排序(让数组接近有序)
2.插入排序
预排序:
1.gap组越大,大的可以更快地跳到后面,小的数可以越快跳到前面,就越不接近有序
2.gap组越小,跳地越慢,越接近有序,gap == 1,就相当于插入排序就有序了
//希尔排序
void Shellsort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//+1保证最后一个gap一定是1,就可以进行直接插入排序
//gap > 1是预排序
//gap == 1是直接插入排序
gap = gap / 3 + 1;
for (int i = 0; i < n-gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
时间复杂度的分析:
希尔排序的时间复杂度比较难分析,这里给出大概的时间复杂度是:O(N^1.3)
为什么有gap组呢?
因为假设每组的间隔是gap,0-gap-1是组数,
组数就是gap
假设有gap组,n个数据,每组就有n/gap个数据
gap = n/3,每组有3个数据
最坏情况下,每组的比较次数*组数
第一次排序的消耗(1+2)*n/3 = n
第二次排序的消耗 (1+2+…+8)*n/9 = 4 * n
最后一次排序的消耗 ,最后一次排序很接近有序了
gap == 1了,就是直接插入排序了,就等于N
比如第一次排序对第二次排序有影响,因为前面一部分有序了,而后面第二次排序可能部分也有序了,所以第二次排序消耗是少于4n的
前面的排序对后面的排序有影响,所以不好算