目录
3.3.1 队列的定义
- 队列简称队,它也是一种运算受限的线性表
- 队列只能选取一个端点进行插入操作,另一个端点进行删除操作
- 把进行插入的一端称做队尾(rear), 进行删除的一端称做队首或队头(front)
- 向队列中插入新元素称为进队或入队,新元素进队后就成为新的队尾元素
- 从队列中删除元素称为出队或离队,元素出队后,其后继元素就成为队首元素
队列的主要特点是先进先出,所以又把队列称为先进先出表
队列抽象数据类型=逻辑结构+基本运算(运算描述),队列的基本运算如下:
- InitQueue(&q):初始化队列。构造一个空队列q。
- DestroyQueue(&q):销毁队列。释放队列q占用的存储空间。
- QueueEmpty(q):判断队列是否为空。若队列q为空,则返回真;否则返回假。
- enQueue(&q,e):进队列。将元素e进队作为队尾元素。
- deQueue(&q,&e):出队列。从队列q中出队一个元素,并将其值赋给e。
思考题
队列和线性表有什么不同? 队列和栈有什么不同?
解析:
| 相同点 | 不同点 |
| 都是线性结构 | ①运算规则不同
|
| 都是逻辑结构的概念 | |
| 都可以用顺序存储或链表存储 | ② 用途不同
|
| 栈和队列是两种特殊的线性表,对插入、删除运算加以限制 |
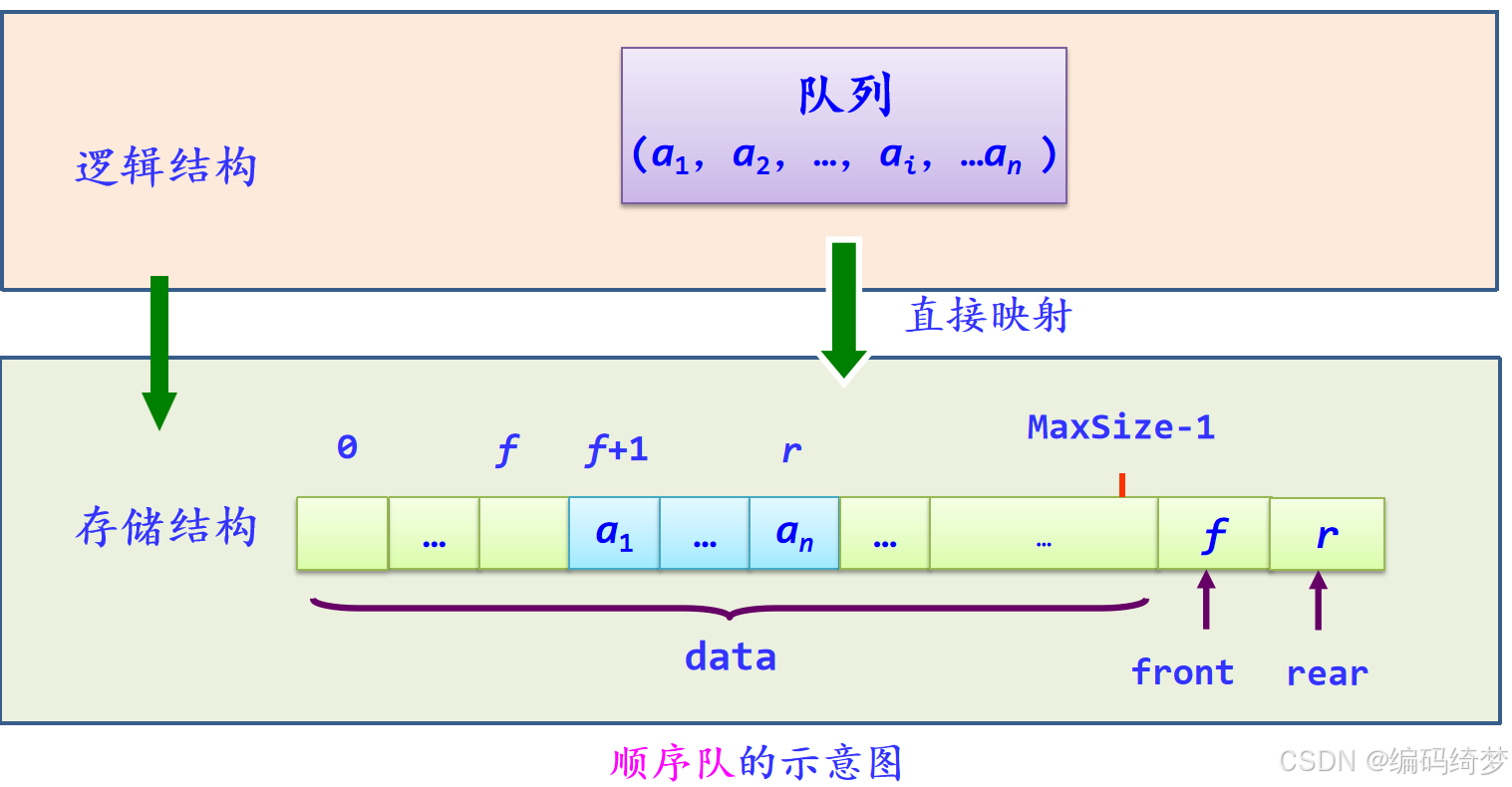
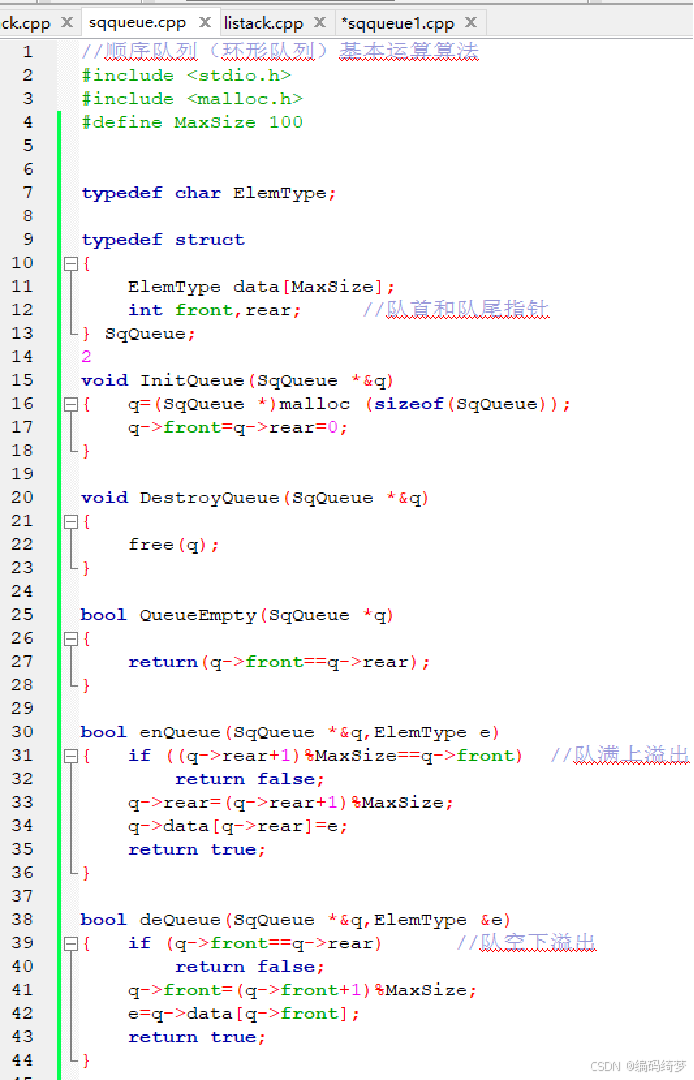
3.3.2 队列的顺序存储结构及其基本运算的实现
1.队列的顺序存储结构定义
顺序队类型SqQueue声明如下:
typedef struct
{ ElemType data[MaxSize]; //存放队中元素
int front,rear; //队首和队尾指针
} SqQueue;//顺序队类型
因为队列两端都在变化,所以需要两个“指针”来标识队列的状态

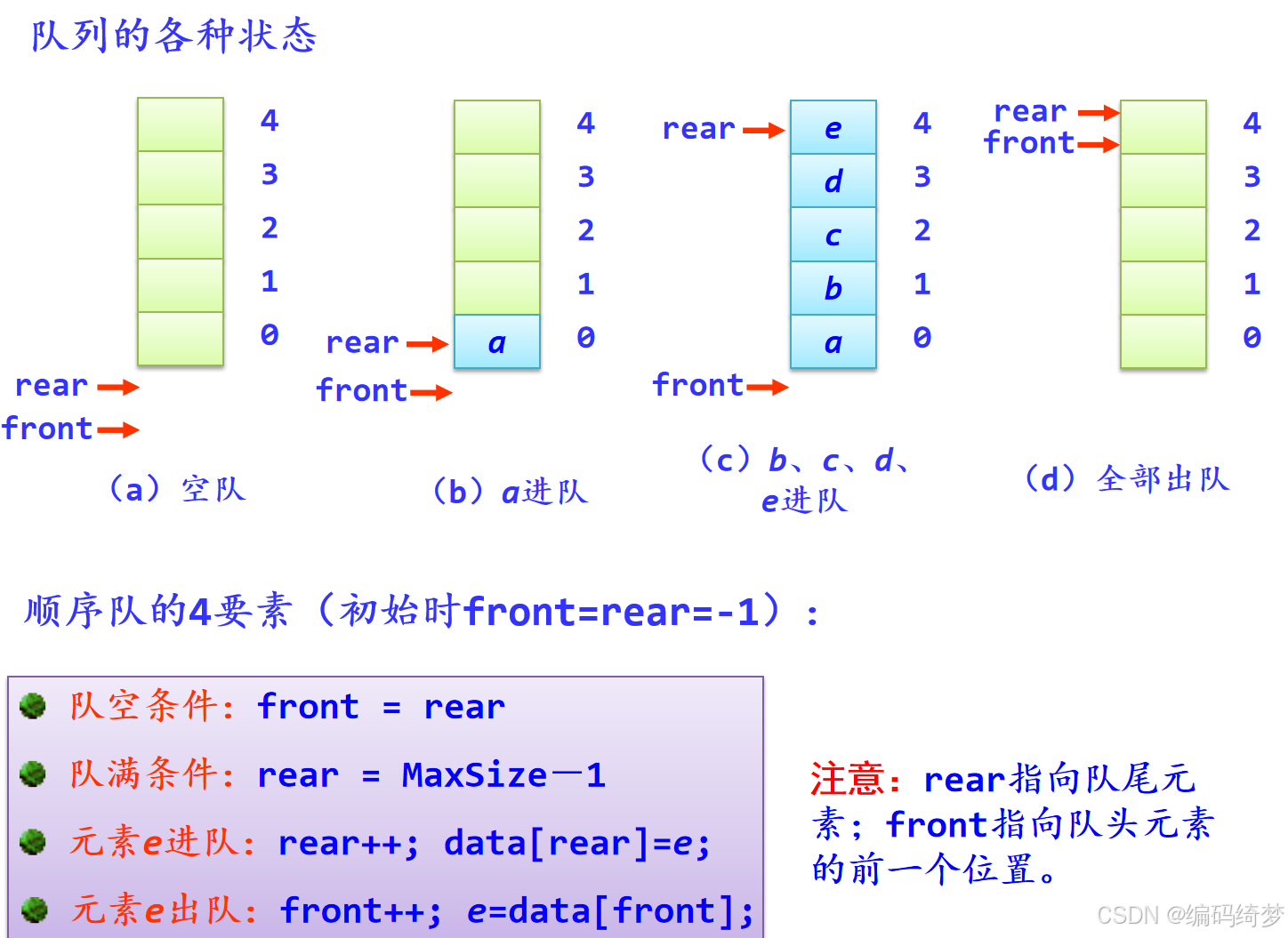
2.顺序队中实现队列的基本运算
(1)初始化队列InitQueue(q) 构造一个空队列q
将front和rear指针均设置成初始状态即-1值,(初始值-1,即当前下标为0的位置)算法如下:
void InitQueue(SqQueue *&q)
{ q=(SqQueue *)malloc (sizeof(SqQueue));
q->front=q->rear=-1;
}
(2)销毁队列DestroyQueue(q)
释放队列q占用的存储空间,算法如下:
void DestroyQueue(SqQueue *&q)
{
free(q);
}
(3)判断队列是否为空QueueEmpty(q)
若队列q满足q->front==q->rear条件,则返回true;否则返回false,算法如下:
bool QueueEmpty(SqQueue *q)
{
if(q!=NULL) //如果q = NULL,则运行报错
return(q->front==q->rear);
}
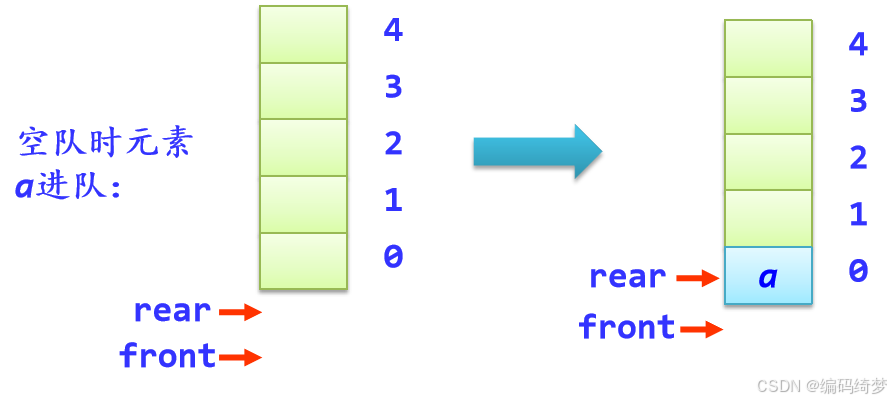
(4)进队列enQueue(q,e)
在队列不满的条件下,先将队尾指针rear循环增1,然后将元素添加到该位置,算法如下:
bool enQueue(SqQueue *&q,ElemType e)
{ if (q->rear==MaxSize-1) //队满上溢出,q->rear==MaxSize-1表示堆队满
return false;
q->rear++; //队尾增一
q->data[q->rear]=e;//在rear位置插入元素e
return true;
}
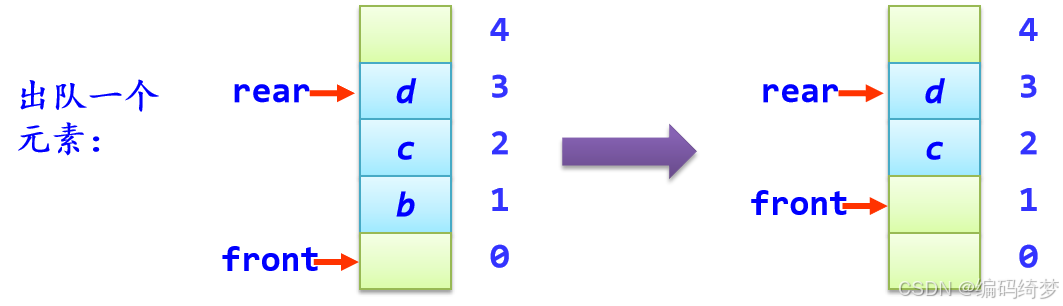
(5)出队列deQueue(q,e)
在队列q不为空的条件下,将队首指针front循环增1,并将该位置的元素值赋给e,算法如下:
bool deQueue(SqQueue *&q,ElemType &e)
{ if (q->front==q->rear) //队空下溢出
return false;
q->front++;
e=q->data[q->front];
return true;
}
3.在环形队中实现队列的基本运算(或循环队列)
环形列队操作主要解决假上溢问题!!!
这是因为采用rear==MaxSize-1作为队满条件的缺陷,
当队满条件为真时,队中可能还有若干空位置, 这种溢出并不是真正的溢出,称为假溢出。
如何利用下面空闲的0和1呢?
解决方案:把数组的前端和后端连接起来,形成一个环形的顺序表,即把存储队列元素的表从逻辑上看成一个环,称为环形队列或循环队列
环形队列(循环队列):
实际上内存地址一定是连续的,不可能是环形的,这里是通过逻辑方式实现环形队列,也就是将rear++和front++改为:
- rear=(rear+1)%MaxSize
- front=(front+1)%MaxSize
上面这样做是为了保证不越界
- 如图说明了环形列队操作的几种状态,在这里假设MaxSize等于5
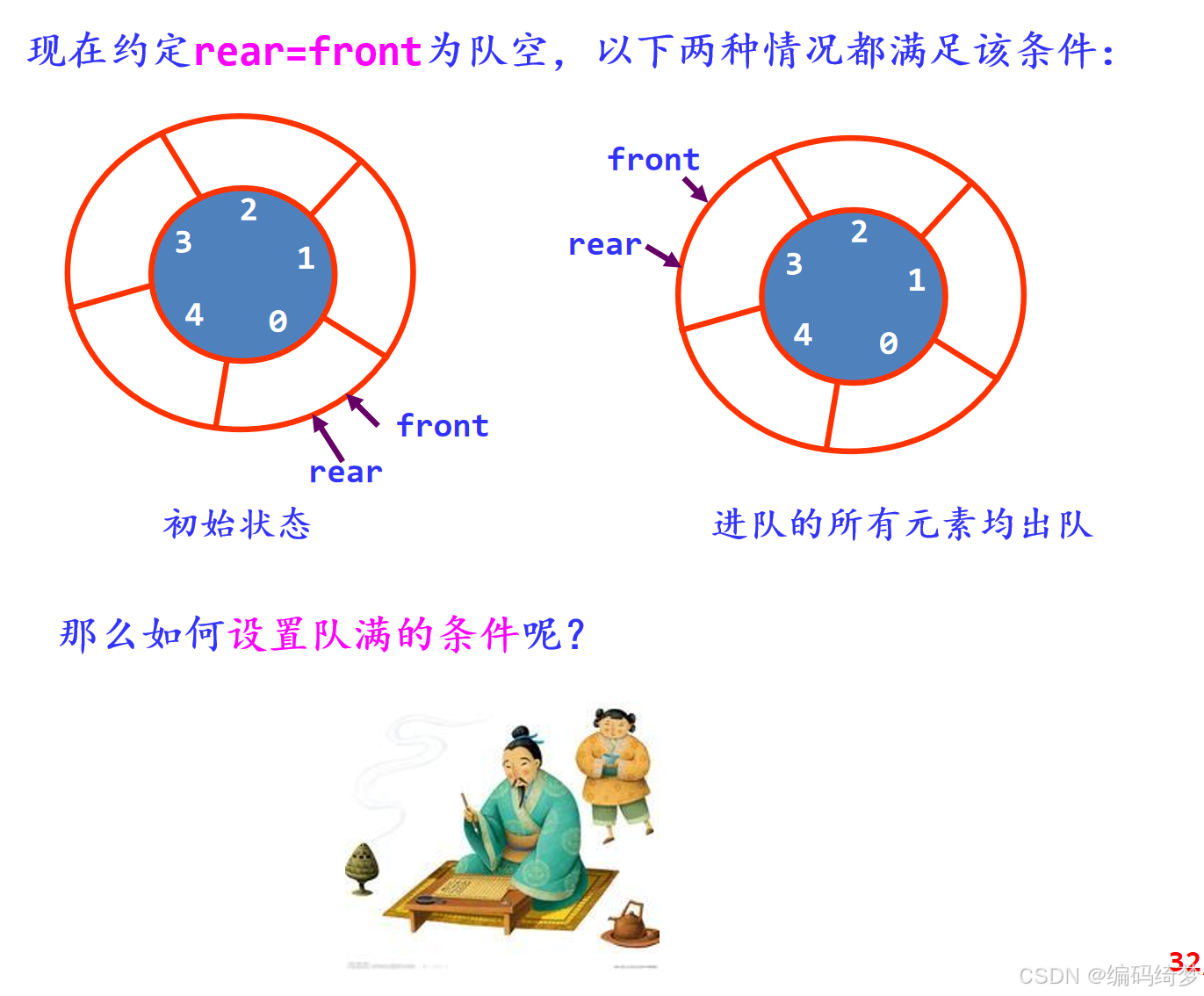
环形队列的4要素:
- 队空条件:front = rear
- 队满条件:(rear+1)%MaxSize = front
- 进队e操作:rear=(rear+1)%MaxSize; 将e放在rear处
- 出队操作:front=(front+1)%MaxSize; 取出front处元素e
在环形队列中,实现队列的基本运算算法与非环形队列类似,只是改为上述4要素即可
代码实现:
(1)进队列:enQueue(&q,e)
在列队不满的条件下先将队尾指针rear循环增一,然后将元素插到该位置,算法如下:
bool enQueue(SqQueue *&q,ElemType e)
{ if ((q->rear+1)%MaxSize==q->front) //队满上溢出
return false;
q->rear=(q->rear+1)%MaxSize;
q->data[q->rear]=e;
return true;
}(5)出队列deQueue(&q,&e)
在队列q不为空的条件下,将队首指针front循环增1,并将该位置的元素值赋给e,算法如下:
bool deQueue(SqQueue *&q,ElemType &e)
{ if (q->front==q->rear) //队空下溢出
return false;
q->front = (q->front+1) % MaxSize;
e = q->data[q->front];
return true;
}
例题:
对于环形队列来说,如果知道队头指针和队列中元素个数,则可以计算出队尾指针。也就是说,可以用队列中元素个数代替队尾指针。
设计出这种环形队列的初始化、入队、出队和判空算法。
解析:

以上是求数据元素个数的方法分析,公式:count = (rear-front+MaxSize)%MaxSize
全部代码如下:
3.顺序队列和循环队列的不同
- 显然环形队列比非环形队列更有效利用内存空间,即环形队列会重复使用已经出队元素的空间。不会出现假溢出。
- 但如果算法中需要使用所有进队的元素来进一步求解(在环形队列中,出队元素空间可能被新进队的元素覆盖),此时可以使用非环形队列。
3.3.3 队列的链式存储结构及其基本运算的实现
1.队列的链式存储结构定义
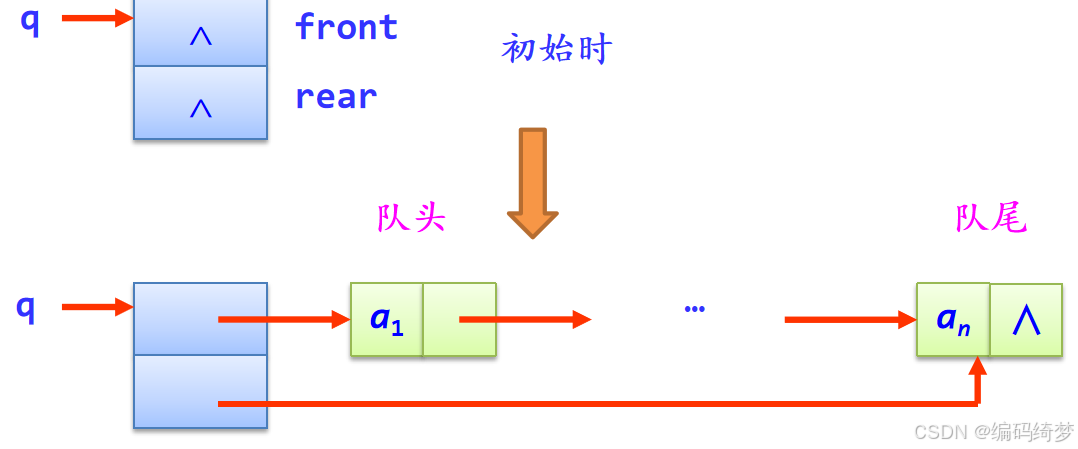
采用链表存储的队列称为链队,这里采用不带头结点的单链表实现
链队的进队和出队操作演示:
2.队列的链式存储结构基本运算的实现
(1)链队中数据结点的类型DataNode声明如下:
typedef struct qnode
{ ElemType data; //数据元素
struct qnode *next;//下一个结点指针
} DataNode;//链队数据结点类型
链队头结点(或链队结点)的类型LinkQuNode声明如下:
typedef struct
{ DataNode *front; //指向单链表队头结点
DataNode *rear; //指向单链表队尾结点
} LinkQuNode; 链队的4要素:
- 队空条件:front=rear=NULL
- 队满条件:不考虑
- 进队e操作:将包含e的结点插入到单链表表尾
- 出队操作:删除单链表首数据结点
(2)初始化队列InitQueue(q)
构造一个空队列,即只创建一个链队头结点,其front和rear域均置为NULL,不创建数据元素结点,算法如下:
void InitQueue(LinkQuNode *&q)
{ q=(LinkQuNode *)malloc(sizeof(LinkQuNode));
q->front=q->rear=NULL;
}
(3)销毁队列DestroyQueue(q)
释放队列占用的存储空间,包括链队头结点和所有数据结点的存储空间,算法如下:
void DestroyQueue(LinkQuNode *&q)
{ DataNode *p=q->front,*r; //p指向队头数据结点
if (p!=NULL) //释放数据结点占用空间
{
r=p->next;
while (r!=NULL)
{
free(p);
p=r;
r=p->next;
}
}
free(p);
free(q); //释放链队结点占用空间
}
(4)判断队列是否为空QueueEmpty(q)
若链队结点的rear域值为NULL,表示队列为空,返回true;否则返回false,算法如下:
bool QueueEmpty(LinkQuNode *q)
{
return(q->rear==NULL);
}
(5) 进队enQueue(q,e)
考虑情况:原队列为空 &&原队列非空
void enQueue(LinkQuNode *&q,ElemType e)
{ DataNode *p;
p=(DataNode *)malloc(sizeof(DataNode));//创建新结点
p->data=e;
p->next=NULL;
if (q->rear==NULL) //若链队为空,新结点是队首结点又是队尾结点
q->front=q->rear=p;
else //若链队不空
{
q->rear->next=p; //将p结点链到队尾,并将rear指向它
q->rear=p;
}
}
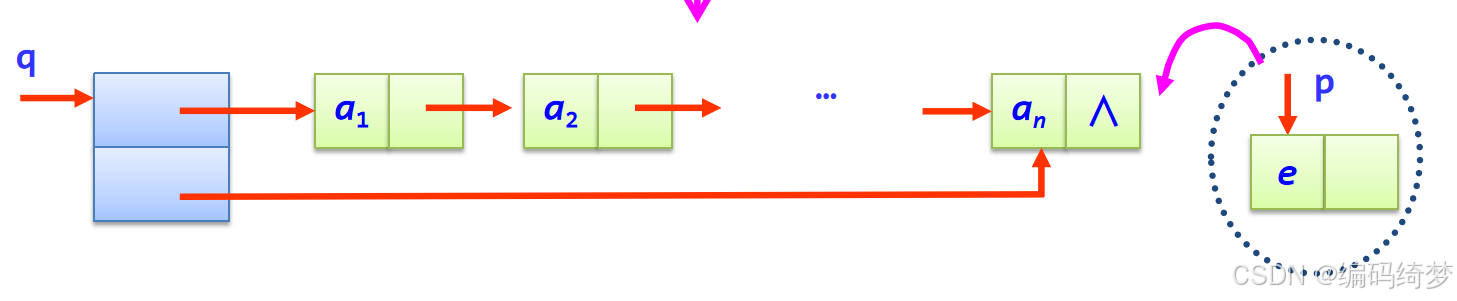
核心代码示意图如下:q->rear->next=p;
q->rear=p;
(6)出队deQueue(q,e)
考虑情况:1.原队列为空
2.原队列只有一个结点
3.其他情况
bool deQueue(LinkQuNode *&q,ElemType &e)
{ DataNode *t;
if (q->rear==NULL)
return false; //队列为空
t=q->front; //t指向第一个数据结点,即首结点
if (q->front==q->rear) //缘来队列中只有一个结点时
q->front=q->rear=NULL;
else //队列中有两个或者两个以上结点时
q->front=q->front->next;
e=t->data;
free(t);
return true;
}
核心代码示意图如下:q->front=q->front->next;
(7)对应的队列基本运算算法如下:
运行结果如下:
3.思考题
链队和顺序队两种存储结构有什么不同?
解析:
队列分为顺序存储结构和链式存储结构。
(1)链式存储结构其实就是线性表的单链表,只是只能在对头出元素,队尾进元素而已。 队列的顺序存储结构的缺点——“假溢出”。 循环队列的顺序结构能解决“假溢出”,但是循环队列必须指定出队列的长度,所以说它并不完美。
(2)我们可以用链式存储结构的方式来弥补上述的不足