Bootstrap

平衡二叉搜索树之 红黑 树的模拟实现【C++】

文章目录

红黑树的简单介绍

定义

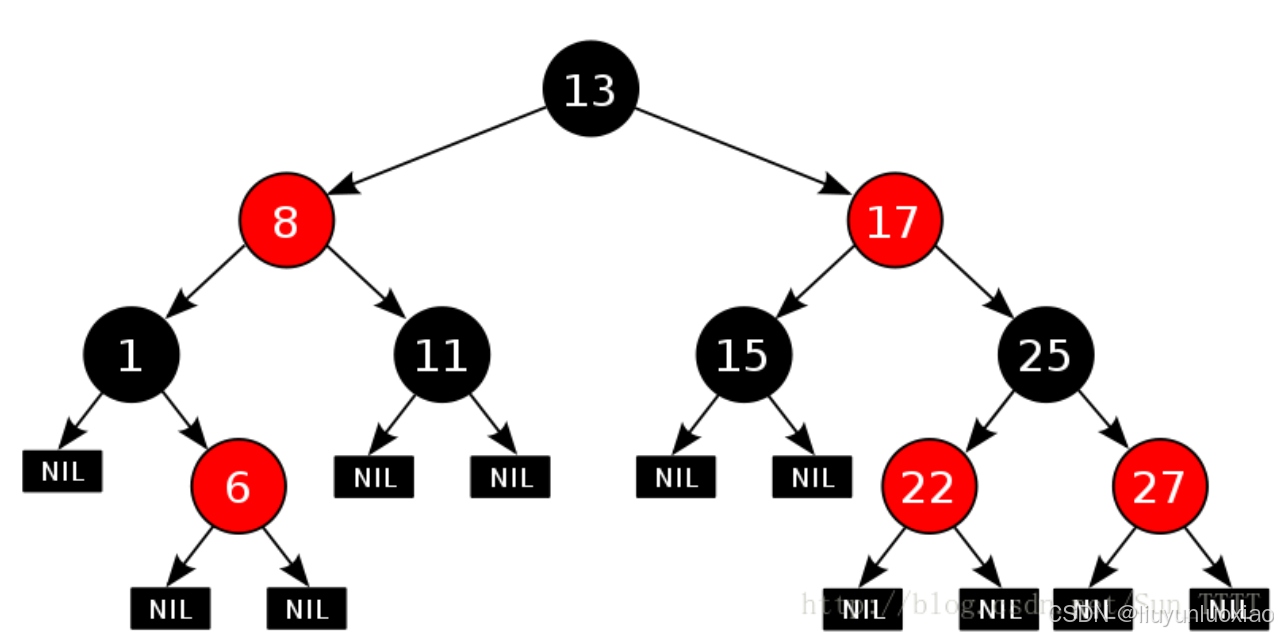
红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，只能是Red或Black。
通过对任何一条从根到空节点的路径上各个结点着色方式的限制
红黑树确保没有一条路径会比其他路径长出俩倍，即最长路径的长度最多是最短路径长度的两倍，这样的话就能保证红黑树是接近平衡的树

在这里插入图片描述

红黑树的特性

红黑树通过以下特性来保持树的平衡，保证最长路径的长度最多是最短路径长度的两倍：

  1. 节点颜色：每个节点只能是红色或黑色。

  2. 根节点：树的根节点是黑色。

  3. 红色规则：如果一个节点是红色，则它的两个子节点都是黑色（也就是说，一条路径不能有两个连续的红色节点）。

  4. 黑色高度：从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

  5. 空节点：所有的空节点（NIL节点，通常是叶子节点的子节点）都是黑色。

为什么满足上面的特性，红黑树就能保证：最长路径的长度最多是最短路径长度的两倍呢？

其实很好理解

因为
特性2：根节点是黑的

特性4：每条路径的黑色节点个数是相同的

特性5：所有的空节点（NIL节点，通常是叶子节点的子节点）都是黑色。

那么任何一个红黑树可能出现的最短路径就是只有黑色节点的路径，因为每条路径的黑色节点个数是相同的

而任何一个红黑树可能出现的最长路径就是一黑一红交替的路径

为什么？

因为
特性1：每个节点只能是红色或黑色

特性3：每一条路径都不可能出现连续的红色节点

特性4：每条路径的黑色节点个数是相同的
所以最短路径和最长路径的黑色节点个数一样

所以最长也只能是黑红节点交替出现

因此
可能的最短的路径，是全黑节点

可能的最长路径是一黑一红，交替出现的路径，红黑节点个数相同

所以
如果全黑节点的路径长度为h
那么一黑一红交替出现的路径长度最多只能是2*h

红黑树的应用

红黑树是一种高效的自平衡二叉搜索树，因其出色的性能和良好的平衡特性，在计算机科学中被广泛应用。以下是红黑树的一些主要应用场景：

  1. Java 和 C++ 中的集合和数据结构：

    • 在 Java 中，红黑树被用于实现 TreeSet 和 TreeMap，分别提供有序集合和有序映射的功能。
    • 在 C++ 中，红黑树是 std::set、std::multiset、std::map 和 std::multimap 的底层数据结构。

  2. 数据库索引：

    • 红黑树常用于数据库系统中，作为索引结构来提高数据查询和更新的效率。
      通过维持数据的有序性和快速搜索特性，红黑树能够有效地管理大量数据。

  3. 操作系统的内存管理：

    • 在操作系统中，红黑树可用于管理内存分配。例如，在 Linux 的虚拟内存管理中，红黑树被用来维护页面分配的信息，确保内存的高效使用。

  4. 文件系统和文件管理：

    • 在文件系统中，红黑树可以用来存储文件元数据，比如文件名、大小和修改时间等信息，以便快速检索和排序。

  5. 网络协议和算法：

    • 在一些网络协议的实现中，红黑树可以用来管理连接状态或路由表，以实现高效的数据包转发和路由决策。

  6. 图形渲染和游戏开发：

    • 在图形渲染和游戏开发中，红黑树可用于管理场景中的物体，通过快速搜索和排序来优化渲染列表。

  7. 科学计算和数据分析：

    • 在科学计算和数据分析中，红黑树可以用于管理大量的有序数据，提供快速的搜索和更新操作，这对于时间序列数据的处理尤为重要。

红黑树可以确保数据结构的稳定性和效率，对于处理大量动态变化的数据集合尤为重要。

全部的实现代码放在了文章末尾

准备工作

创建两个文件，一个头文件RBTree.hpp，一个源文件test.cpp

【因为模板的声明和定义不能分处于不同的文件中，所以把成员函数的声明和定义放在了同一个文件RBTree.hpp中】

  1. RBTee.hpp：存放包含的头文件，命名空间的定义，成员函数和命名空间中的函数的定义

  2. test.cpp：存放main函数，以及测试代码

包含头文件

  • iostream：用于输入输出
  • cmath:提供数学函数

类的成员变量和红黑树节点的定义

红黑树类的成员变量只有一个，就是指向红黑树的根节点的指针

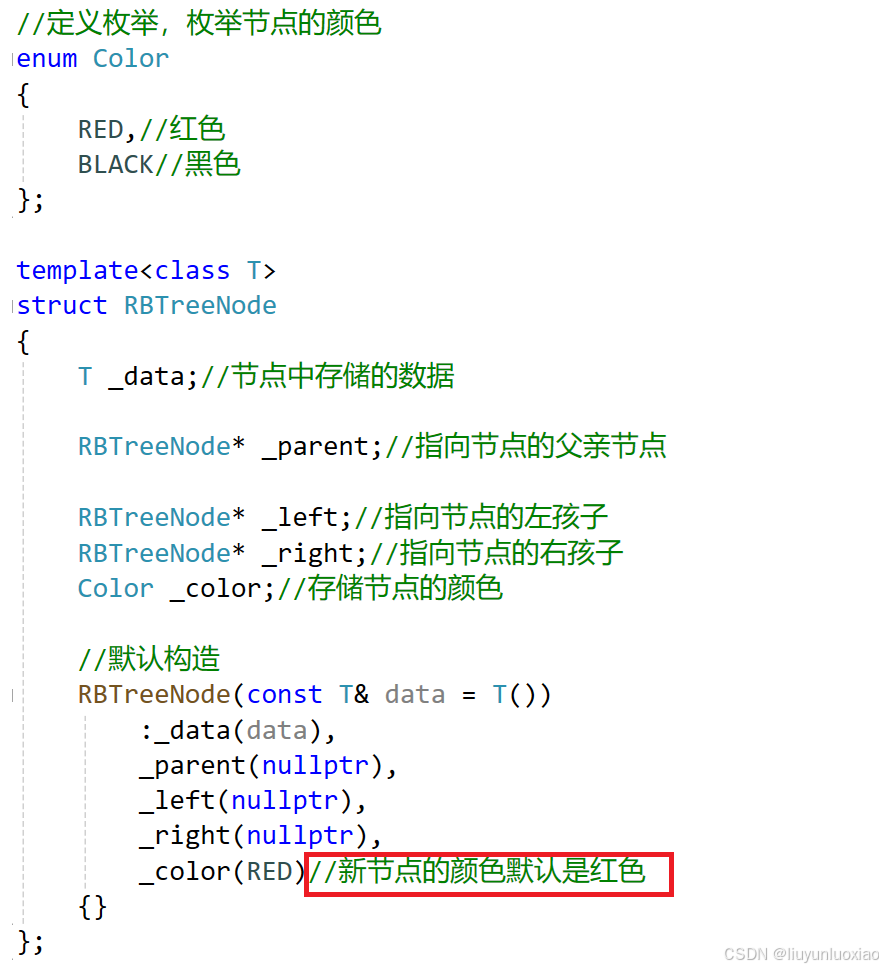
在这里插入图片描述

红黑树的节点类：
在这里插入图片描述
为什么红黑树新插入的节点【或者新节点】一定是红色的？

其实就是维护成本的问题：

1.如果新插入的节点为黑色

因为插入之前，这棵树一定是红黑树

所以他的每一条路径上的黑色节点个数都相同

但是因为你新插入了一个黑色的，这一条路径就会比其他路径多一个黑色节点，为了保持红黑树的规则（每一条路径上的黑色节点个数都相同）

就得想办法让每一条路径也都增加一个黑色节点，维护成本太高了

2.如果新插入的节点为红色

① 新插入的节点的父亲为黑色，就可以直接结束了，因为满足红黑树的所有规则

②就算新插入的节点的父亲为红色，调整的情况也只有两种，维护成本更低

构造函数和拷贝构造

构造函数没什么好说的，默认构造就行了

RBTree() 
	:_root(nullptr)
{}

拷贝构造：
因为节点都是从堆区new出来的，所以要深拷贝

使用递归实现深拷贝：
因为拷贝构造不能有多余的参数，但是递归函数又必须使用参数记录信息
在这里插入图片描述

然后在拷贝构造里面调用一下这个函数就行了

RBTree(const RBTree& obj)
{
	_root = Copy(obj._root, nullptr);
}

swap和赋值运算符重载

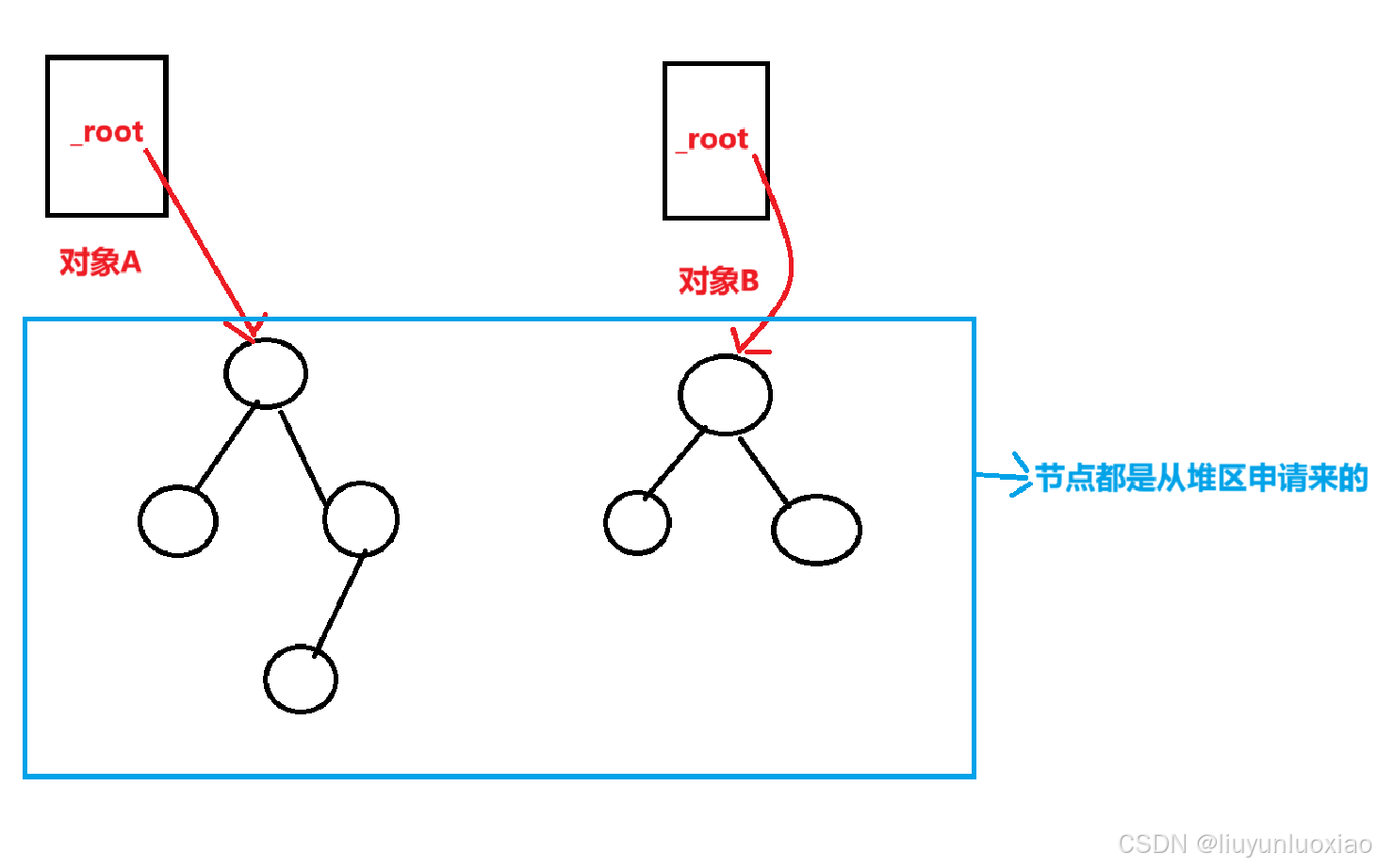
交换两颗红黑树的本质就是交换两颗数的资源（数据），而它们的资源都是从堆区申请来的，然后用指针指向这些资源
在这里插入图片描述

并不是把资源存储在了红黑树对象中

所以资源交换很简单，直接交换_root指针的指向即可

void Swap(RBTree& obj)
{
	std::swap(_root, obj._root);
}

赋值运算符重载

RBTree& operator=(RBTree obj)
{
	this->Swap(obj);
	return *this;
}

为什么上面的两句代码就可以完成深拷贝呢？
这是因为：

使用了传值传参，会在传参之前调用拷贝构造，再把拷贝构造出的临时对象作为参数传递进去

赋值运算符的左操作数，*this再与传入的临时对象obj交换，就直接完成了拷贝

在函数结束之后，存储在栈区的obj再函数结束之后，obj生命周期结束

obj调用析构函数，把指向的从*this那里交换来的不需要的空间销毁

析构函数

使用递归遍历，把所有从堆区申请的节点都释放掉：
因为析构函数不能有多余的参数，但是递归函数又必须使用参数记录信息
所以再封装一个成员函数，专门用来递归释放：

在这里插入图片描述

然后在拷贝构造里面调用一下这个函数就行了

~RBTree()
{
	Destroy(_root);
	_root = nullptr;
}

find

具体流程：
从根节点开始，将目标值（传入的key）与当前节点的key进行比较。
如果目标值小于当前节点值，则在左子树中继续查找；
如果目标值大于当前节点值，则在右子树中继续查找。

这个过程一直进行，直到找到与目标值或者到达空节点为止。

把上述过程转成代码：

在这里插入图片描述

insert【重要】

红黑树就是在二叉搜索树的基础上节点有了颜色，因此红黑树也可以看成是二叉搜索树。

那么AVL树的插入过程可以分为两步：

  1. 先按照二叉搜索树的方式插入新节点

  2. 再调整颜色，维护红黑树的规则

第一步：按照二叉搜索树的方式插入新节点

插入的具体过程如下：

  1. 树为空，则直接新增节点，赋值给二叉搜索树的成员变量_root指针

  2. 树不空，则按照查找（find）的逻辑找到新节点应该插入的位置

  3. 树不空，如果树中已经有了一个节点的key值与要插入的节点的key相同，就插入失败

这个过程一直进行，直到找到与传入的key相等的节点或者到达空节点为止。

把上述过程转成代码：

在这里插入图片描述

第二步：调整颜色，维护红黑树的规则

颜色调整分以下3种情况：

  1. 新插入的节点（cur）的父亲节点（parent）颜色为黑
  2. 新插入的节点（cur）的父亲节点（parent）颜色为红，且叔叔（uncle）节点不为空且为红
  3. 新插入的节点（cur）的父亲节点（parent）颜色为红，且叔叔（uncle）节点为空或者为黑

情况一：新插入的节点的父亲节点颜色为黑

此时插入节点，并没有违反任何红黑树规则，所以不需要调整颜色/树的结构

直接结束插入就行

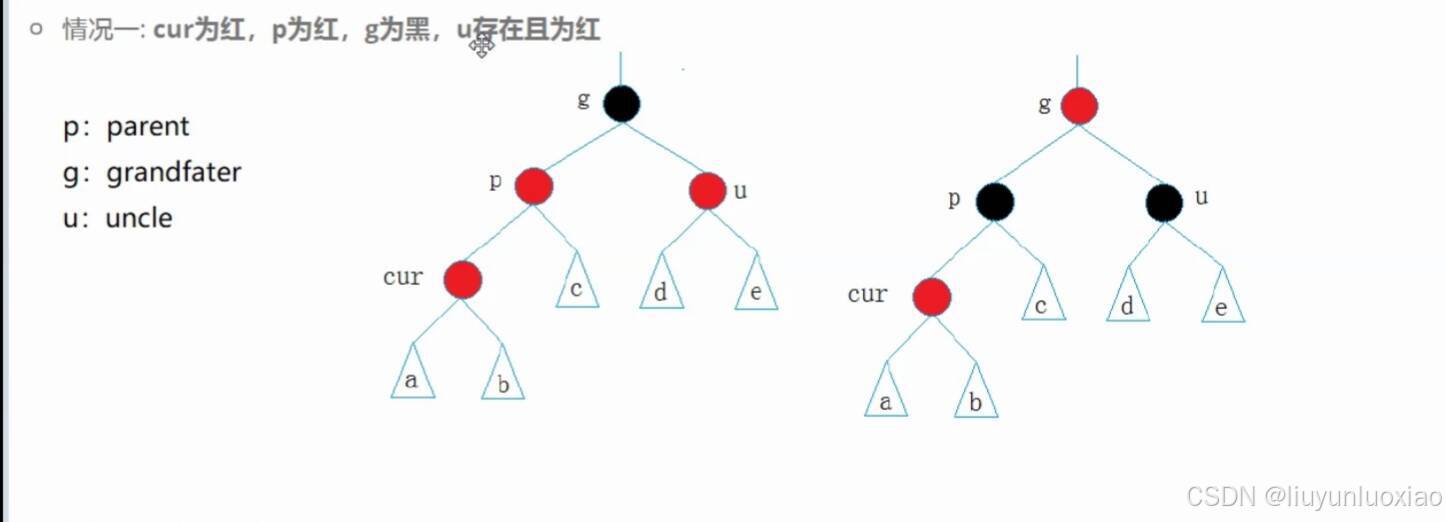
情况二：新插入的节点的父亲节点颜色为红，且叔叔节点不为空且为红

请添加图片描述
（cur为新插入的节点，g是爷爷节点，u是父亲的兄弟节点；a，b，c，d，e是都是符合条件的红黑树）
cur的位置是不固定的
cur也可以是上图的c，d，e
cur的p，g，u相应的改变即可
最主要看的是cur和它的g，p，u的颜色，是否满足情况一

因为插入的节点的颜色为红色，而且它的父亲节点也是红色
那么它就违反了红黑树的第3条规则：同一路径不能出现连续的红色节点
所以必须进行调整。
因为叔叔节点不为空且为红，所以没有严重违反红黑树的规则，只需要对颜色进行调整即可

所以调整方案是：

①把p，u都变黑，把g变红：这样就能让连续的红色节点去除，但是g（爷爷接节点）变成红色了，g的父亲节点也可能是红色
所以需要
②再把g看作cur继续循环向上调整，再根据新的c,p,u,g节点的颜色，判断是情况一，情况二还是情况三

具体实现代码：
在这里插入图片描述

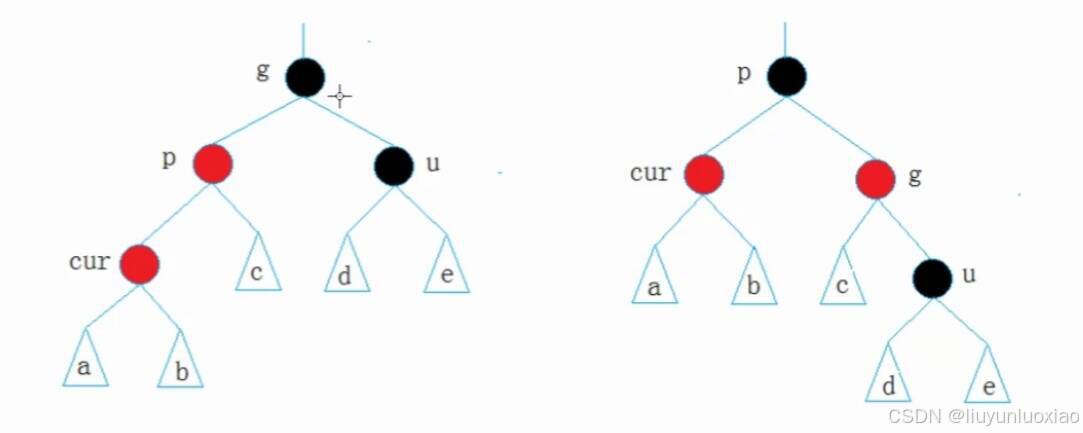
情况三：新插入的节点的父亲节点颜色为红，且叔叔节点为空或者为黑

请添加图片描述
【此时cur的位置也是不固定的
cur也可以是上图的c，d，e
cur的p，g，u相应的改变即可
最主要看的是cur和它的g，p，u的颜色，是否满足情况二】

因为插入的节点的颜色为红色，而且它的父亲节点也是红色
那么它就违反了红黑树的第3条规则：同一路径不能出现连续的红色节点
所以必须进行调整。
因为叔叔（uncle）节点为空或者为黑，所以严重违反红黑树的规则，需要调整红黑树的部分结构和调整颜色

所以此时的调整方案是：
先旋转[根据cur，p和g的相对位置，进行左旋，右旋，双旋]，再变颜色
【如果不知道旋转是什么的话，可以看我这篇文章：平衡二叉搜索树之 AVL 树的模拟实现【C++】中的怎么旋转】

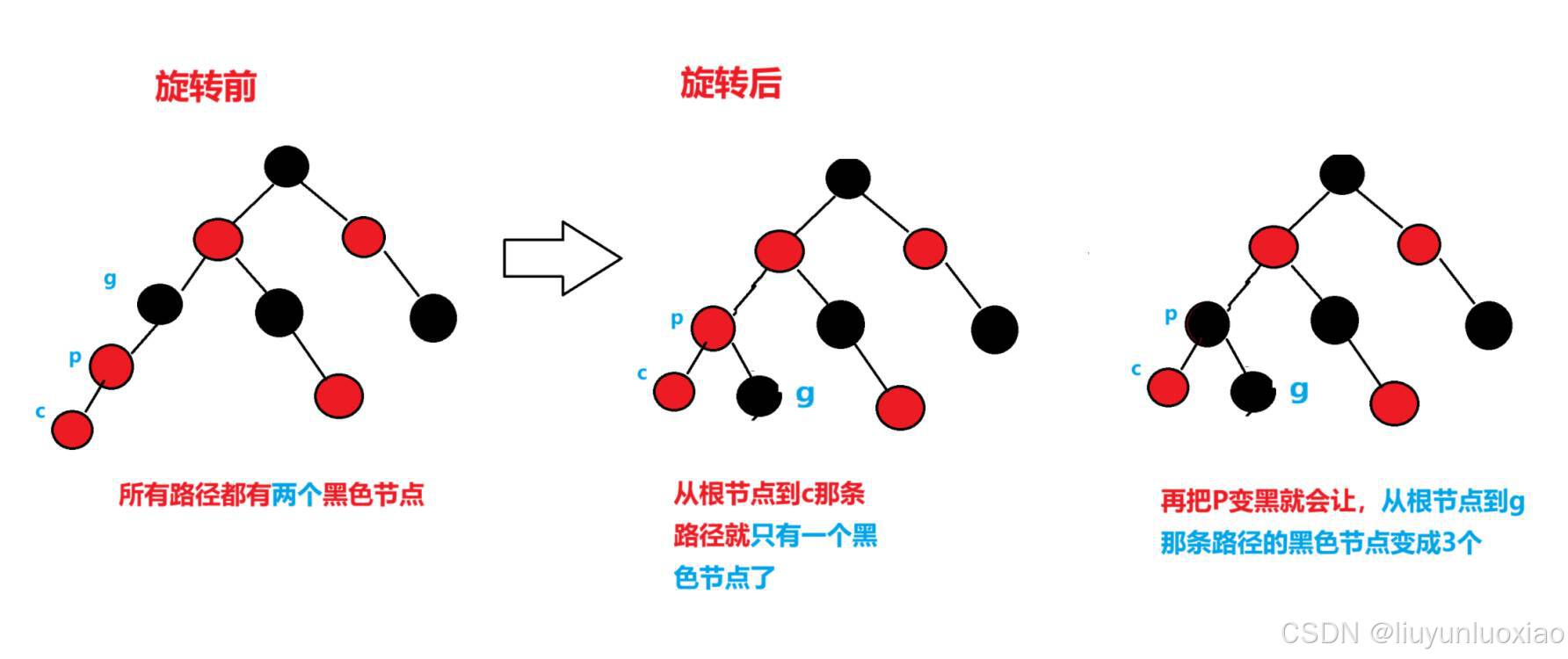
①单旋：p变黑，g变红
因为单旋之后， p就变成了c，p，g及其子树组成的这棵树的根节点
然后又因为g是黑色，所以他旋转下去的话，
那么c那条路径就会比其他路径少一个黑色节点
所以需要把作为新的根节点的p变黑，这样c那条路径的黑色节点数量才会与其他路径上的相同
但是这样又会让g那条路径比其他的路径多一个黑色节点
所以再把g变红
请添加图片描述
②双旋：c变黑，g变红
因为单旋之后， c就变成了c，p，g及其子树组成的这棵树的根节点
然后的推导就与单旋的类似了

具体代码实现：
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

empty

bool Empty()
{
    如果_root为空，那么树就是空的
	return _root == nullptr;
}

size

使用递归实现二叉搜索树的节点个数统计：
因为我们经常使用的stl的容器的size都是没有参数的，但是递归函数又必须使用参数记录信息
所以再封装一个成员函数，专门用来递归：

在这里插入图片描述

然后再size里面调用一下就行了

size_t Size()
{
	return _Size(_root);
}

中序遍历

中序遍历的递归函数：
在这里插入图片描述

然后再调用递归函数

void InOrder()
{
	_InOrder(_root);
}

红黑树和AVL树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O( l o g 2 N log_2 N log2​N)

红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，减少了旋转的次数

所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单
所以实际运用中红黑树更多

全部代码

#define _CRT_SECURE_NO_WARNINGS

#include<iostream>
#include<cmath>
using namespace std;

//定义枚举，枚举节点的颜色
enum Color
{
	RED,//红色
	BLACK//黑色
};

template<class T>
struct RBTreeNode
{
	T _data;//节点中存储的数据

	RBTreeNode* _parent;//指向节点的父亲节点

	RBTreeNode* _left;//指向节点的左孩子
	RBTreeNode* _right;//指向节点的右孩子
	Color _color;//存储节点的颜色

	//默认构造
	RBTreeNode(const T& data = T())
		:_data(data),
		_parent(nullptr),
		_left(nullptr),
		_right(nullptr),
		_color(RED)//新节点的颜色默认是红色
	{}
};


//模板参数T，就是节点中存储的数据的类型
template<class T>
class RBTree
{
	//给节点类重命名
	typedef RBTreeNode<T> Node;
private:
	//指向红黑树的根节点的指针
	Node* _root = nullptr;


public:
	RBTree()
		:_root(nullptr)
	{}

	RBTree(const RBTree& obj)
	{
		_root = Copy(obj._root, nullptr);
	}
	RBTree& operator=(RBTree obj)
	{
		this->Swap(obj);
		return *this;
	}
	~RBTree()
	{
		Destroy(_root);
		_root = nullptr;
	}

	void Swap(RBTree& obj)
	{
		std::swap(_root, obj._root);
	}

	bool Insert(const T& data)
	{
		Node* newnode = new Node(data);

		if (_root == nullptr)
		{
			_root = newnode;
			_root->_color = BLACK;
			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_data < data)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_data > data)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		if (parent->_data > data)
		{
			parent->_left = newnode;
		}
		else
		{
			parent->_right = newnode;
		}
		newnode->_parent = parent;

		cur = newnode;

		//如果新插入的节点的父节点的颜色是  黑色
		// 因为已经符合红黑树的规则了，直接结束插入
		if (parent->_color == BLACK)
			return true;//直接结束
		else//否则
		{
			Node* grandpa = parent->_parent;//爷爷节点

			Node* uncle = nullptr;//叔叔节点，即cur的父亲节点的  兄弟节点

			if (parent == grandpa->_left)//如果parent是左孩子
			{
				uncle = grandpa->_right;//那么它的兄弟节点就是右孩子
			}
			else//如果parent是右孩子
			{
				uncle = grandpa->_left;//那么它的兄弟节点就是左孩子
			}

			//情况二：
			// cur的父亲节点（parent）为红，且叔叔（uncle）节点不为空且为红
			//只需要继续  循环  向上调整
			while (parent->_color == RED && uncle && uncle->_color == RED)
			{
				//调整颜色
				grandpa->_color = RED;
				parent->_color = BLACK;
				uncle->_color = BLACK;

				//如果调整到根节点，就不需要再向上调整了
				if (grandpa == _root)
				{
					//因为根节点只能是黑色
					//所以把爷爷节点（grandpa）的颜色调成黑色
					grandpa->_color = BLACK;
					return true;//直接结束
				}

				//重新赋值
				//继续向上调整
				cur = grandpa;//让原来的爷爷节点作为cur

				parent = cur->_parent;//重新得出新的父亲节点

				//如果新的父亲节点为黑，就和刚插入节点时一样
				// 因为已经符合红黑树的规则了，直接结束插入
				if (parent->_color == BLACK)
					return true;//直接结束

				grandpa = parent->_parent;//重新得出新的爷爷节点

				//重新得出新的叔叔节点
				if (parent == grandpa->_left)
				{
					uncle = grandpa->_right;
				}
				else
				{
					uncle = grandpa->_left;
				}
			}

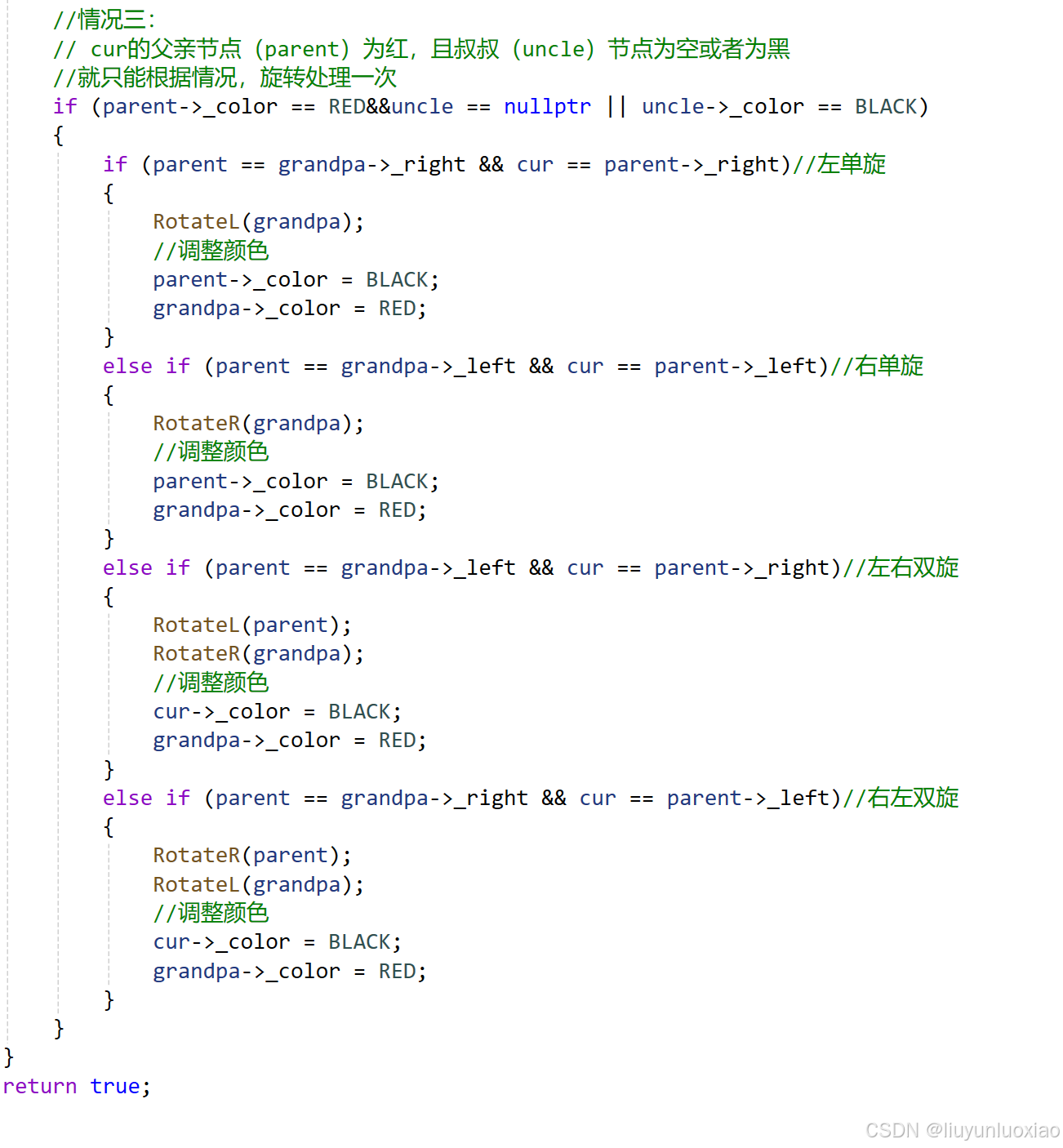
			//情况三：
			// cur的父亲节点（parent）为红，且叔叔（uncle）节点为空或者为黑
			//就只能根据情况，旋转处理一次
			if (parent->_color == RED&&uncle == nullptr || uncle->_color == BLACK)
			{
				if (parent == grandpa->_right && cur == parent->_right)//左单旋
				{
					RotateL(grandpa);
					//调整颜色
					parent->_color = BLACK;
					grandpa->_color = RED;
				}
				else if (parent == grandpa->_left && cur == parent->_left)//右单旋
				{
					RotateR(grandpa);
					//调整颜色
					parent->_color = BLACK;
					grandpa->_color = RED;
				}
				else if (parent == grandpa->_left && cur == parent->_right)//左右双旋
				{
					RotateL(parent);
					RotateR(grandpa);
					//调整颜色
					cur->_color = BLACK;
					grandpa->_color = RED;
				}
				else if (parent == grandpa->_right && cur == parent->_left)//右左双旋
				{
					RotateR(parent);
					RotateL(grandpa);
					//调整颜色
					cur->_color = BLACK;
					grandpa->_color = RED;
				}
			}
		}
		return true;
	}


	Node* Find(const T& data)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_data < data)
			{
				cur = cur->_right;
			}
			else if (cur->_data > data)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
	bool Empty()
	{
		return _root == nullptr;
	}
	size_t Size()
	{
		return _Size(_root);
	}
	size_t Height()
	{
		return _Height(_root);
	}
	bool IsRBTree()
	{
		if (_root == nullptr)
			return true;

		if (_root->_color != BLACK)
			return false;

		int count = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_color == BLACK)
				count++;
			cur = cur->_left;
		}
		return _IsRBTree(_root, count, 0);
	}
private:

	bool _IsRBTree(const Node* root, const int& total, int count)
	{
		if (root == nullptr)
		{
			if (count != total)
				return false;
			else
				return true;
		}

		if (root->_color == RED && root->_parent->_color == RED)
			return false;


		if (root->_color == BLACK)
			count++;


		if (_IsRBTree(root->_left, total, count) == false)
			return false;
		if (_IsRBTree(root->_right, total, count) == false)
			return false;
		return true;
	}
	size_t _Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int left = _Height(root->_left);
		int right = _Height(root->_right);

		return left > right ? left + 1 : right + 1;
	}


	// 左单旋
	void RotateL(Node* parent)
	{
		//记录一下PR和PRL
		Node* PR = parent->_right;
		Node* PRL = PR->_left;

		//把PRL链接在parent的右边
		parent->_right = PRL;

		//因为PRL可能为空，为了防止空指针访问，必须判断一下
		if (PRL != nullptr)
		{
			//PRL不为空，就把它的父亲节点变成parent
			PRL->_parent = parent;
		}

		//把parent链接在PR的左边
		PR->_left = parent;

		//更改PR的父亲节点
		PR->_parent = parent->_parent;

		//只有AVL树的根节点的父亲节点为空
		//所以parent是根节点
		if (parent->_parent == nullptr)
		{
			//PR变成了这颗子树的根，替代了原来parent的位置
			//所以得把AVL树的根节点更新一下
			_root = PR;
		}
		else//如果parent不是根节点
		{
			//PR还是要带替parent的位置
			//所以parent在父亲的左，PR就在左
			//parent在父亲的右，PR就在右
			if (parent == parent->_parent->_left)
				parent->_parent->_left = PR;
			else
				parent->_parent->_right = PR;
		}
		//更新一下parent的父亲节点
		parent->_parent = PR;
	}



	// 右单旋
	void RotateR(Node* parent)
	{
		//记录一下PL和PLR
		Node* PL = parent->_left;
		Node* PLR = PL->_right;

		//把PLR链接在parent的右边
		parent->_left = PLR;

		//因为PLR可能为空，为了防止空指针访问，必须判断一下
		if (PLR != nullptr)
		{
			//不为空，就把它的父亲节点变成parent
			PLR->_parent = parent;
		}

		//把parent链接在PL的左边
		PL->_right = parent;

		//更新PL的父亲节点
		PL->_parent = parent->_parent;

		//只有AVL树的根节点的父亲节点为空
		//所以parent是根节点
		if (parent->_parent == nullptr)
		{
			//PL变成了这颗子树的根，替代了原来parent的位置
			//所以得把AVL树的根节点更新一下
			_root = PL;
		}
		else//如果parent不是根节点
		{
			//PL还是要带替parent的位置
			//所以parent在父亲的左，PL就在左
			//parent在父亲的右，PL就在右
			if (parent == parent->_parent->_left)
				parent->_parent->_left = PL;
			else
				parent->_parent->_right = PL;
		}
		//更新一下parent的父亲节点
		parent->_parent = PL;
	}





	//因为无法直接获取到父亲节点的地址
	//所以需要传参传进来
	Node* Copy(Node* root, Node* parent)
	{
		//空节点不需要拷贝，直接返回nullptr
		if (root == nullptr)
			return nullptr;

		//从堆区申请空间，并初始化节点
		Node* newnode = new Node(root->_data);

		//连接上传入函数的父亲节点
		newnode->_parent = parent;

		//拷贝颜色
		newnode->_color = root->_color;

		//递归拷贝左右子树
		newnode->_left = Copy(root->_left, newnode);
		newnode->_right = Copy(root->_right, newnode);

		return newnode;//返回新节点
	}


	//使用后序遍历进行释放
	void Destroy(Node* root)
	{
		//空节点
		if (root == nullptr)
			return;
		Destroy(root->_left);
		Destroy(root->_right);

		delete root;
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		_InOrder(root->_left);

		cout << root->_data << "  ";

		_InOrder(root->_right);
	}
	size_t _Size(Node* root)
	{
		if (root == nullptr)
			return 0;
		int left = _Size(root->_left);
		int right = _Size(root->_right);

		return left + right + 1;
	}
};

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
el-input设置placeholder字体大小
rabbitmq 基本配置信息
分组函数之rollup、cube函数、grouping sets函数
work-notes（22）：电脑重装后网络不可用，只有一个飞行模式
Qt(二）
通过JS弹出一个等待对话框(以及遮罩层)提示用户
呕血整理JavaScript知识重点（面试复习必备）
MMPose训练流程
Java毕业设计 Spring Boot+vue基于Web的艺术展览馆艺术品管理系统
q-learning精讲
;