阿华代码,不是逆风,就是我疯
你们的点赞收藏是我前进最大的动力!!
希望本文内容能够帮助到你!!
目录
零:二分查找工具
1:最基础模版
mid的写法可以防止溢出
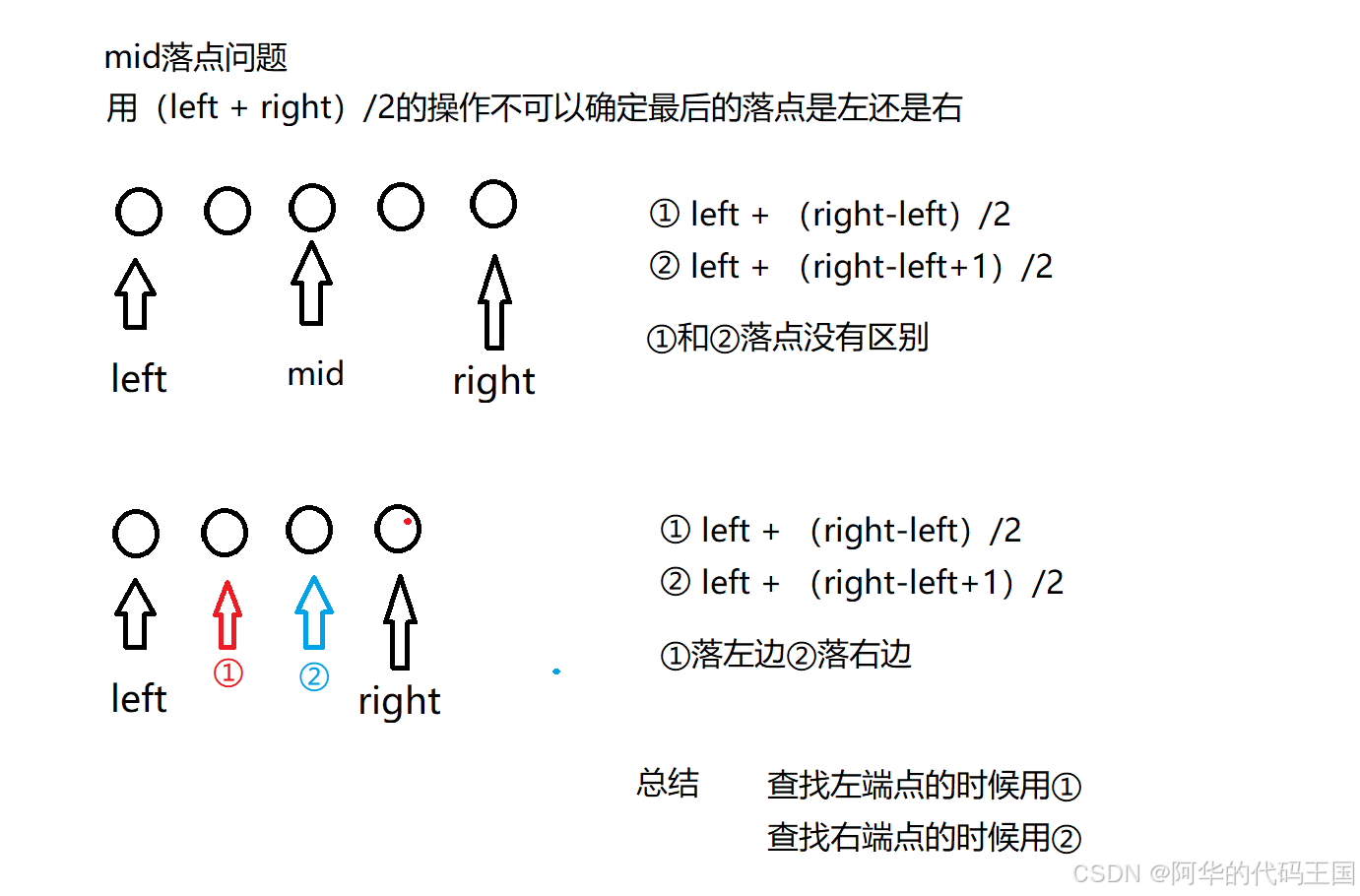
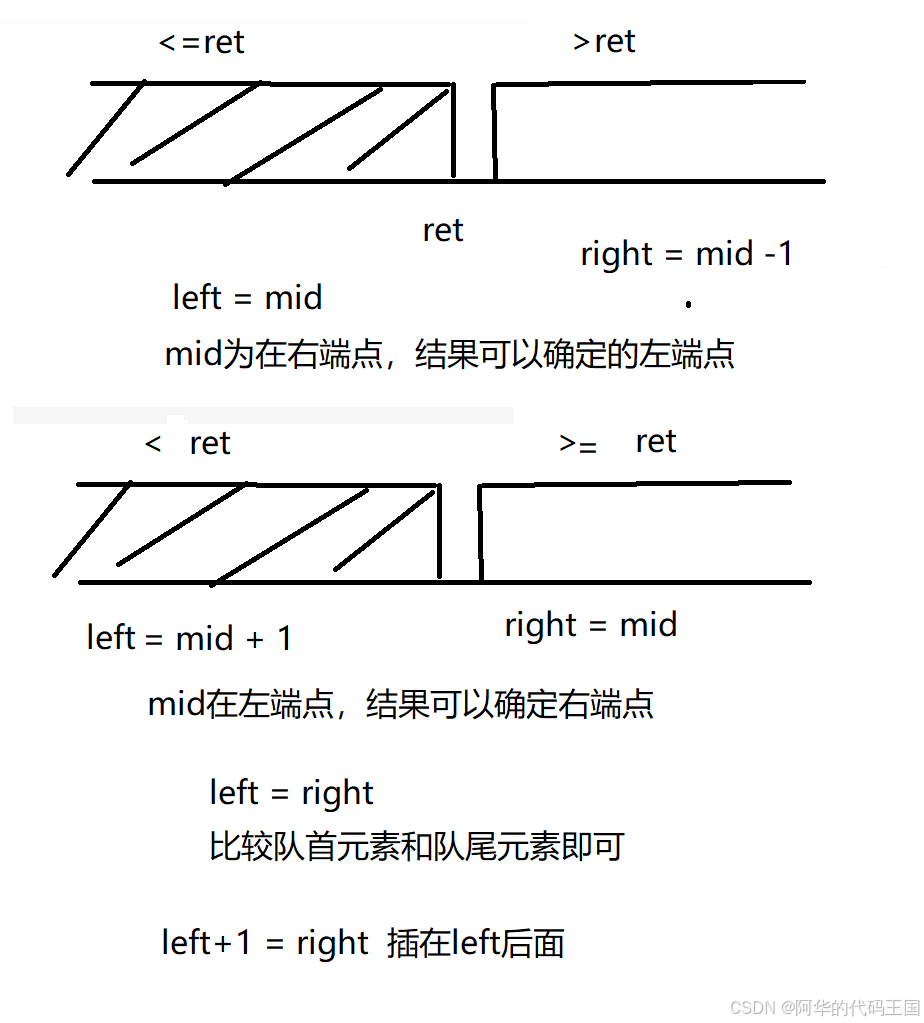
2:mid落点问题
巧妙记忆:循环条件为while(left<right)时,left = mid,想象一下,只剩下两个球,那么我们的mid只能落在右端点,否则left = mid 会造成 left < right 死循环,此时我们确定的是右边的界限
重点:left 和right 根据题目的意思进行设置,然后才是mid的设置根据left和right的设置而设置(这才是这个二分查找的精髓所在)
简单记忆:落在哪个端点确定哪个界限
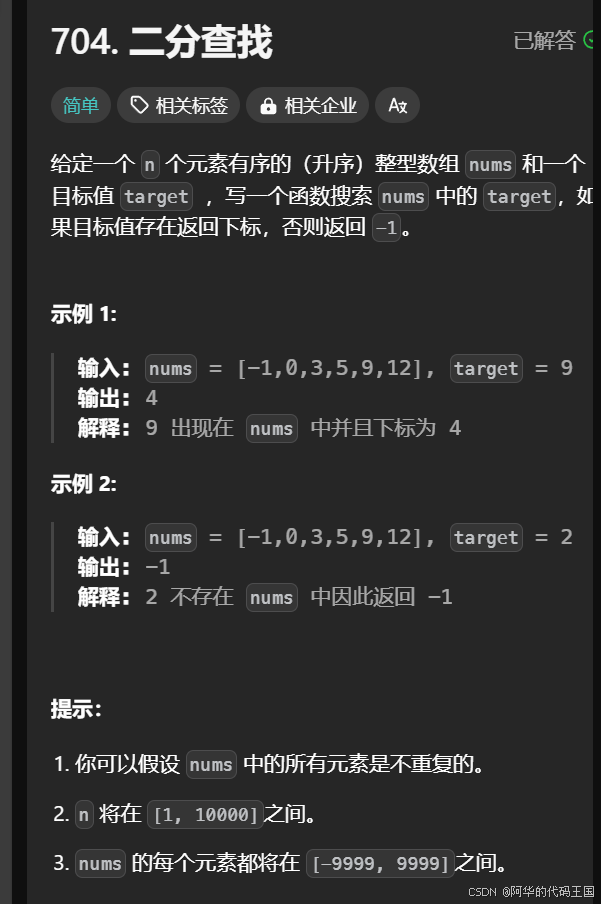
一:最简单的二分
class Solution {
public int search(int[] nums, int target) {
//mid=left + (right - left)/3
//用left移动思想来确定mid的位置,这种写法可以防溢出
int left = 0 , right = nums.length-1 , mid = (left+right)/2;
while(left<=right){
if(nums[mid] < target){
left = mid + 1 ;
mid = (left+right)/2;
}else if(nums[mid] > target){
right = mid - 1;
mid = (left+right)/2;
}else{
return mid;
}
}
return -1;
}
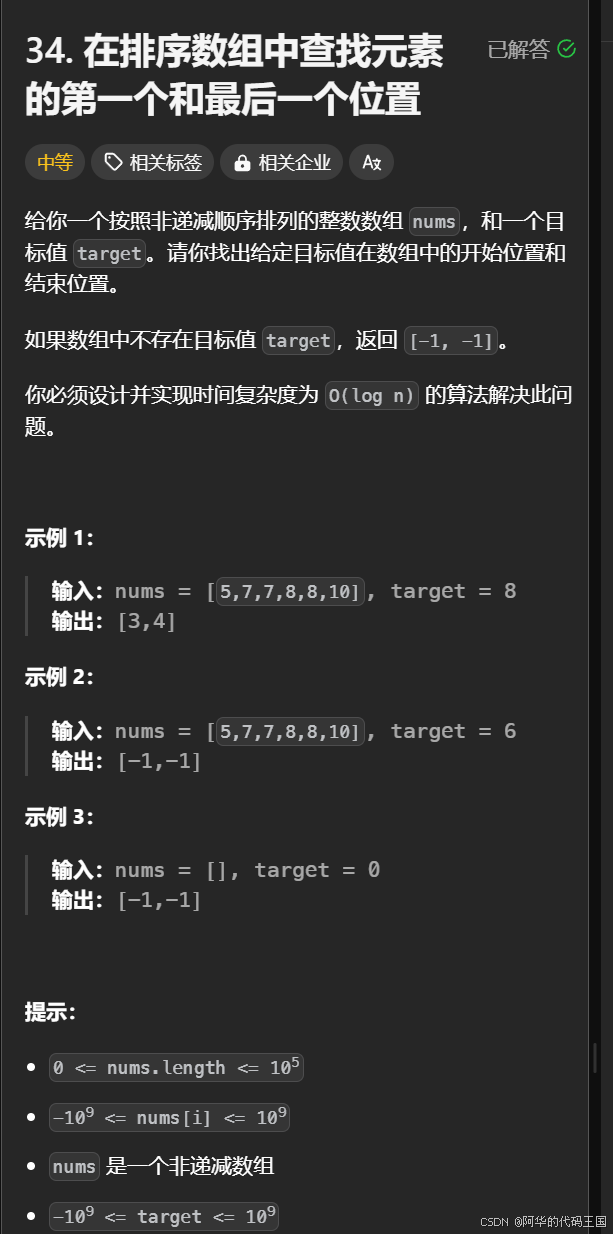
}二:查找元素的位置(可能会有多个)
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] result = new int[]{-1,-1};
if(nums.length == 0 ){
return result;
}
//左端点
int left = 0 , right = nums.length-1 ,targetLeft = 0 , targetRight = 0;
while(left < right){
int mid = left + (right - left )/2;
if(nums[mid] < target){
left = mid + 1;
}else{
right = mid;
}
}
targetLeft = left;
left = 0 ; right = nums.length-1 ;
//右端点
while(left < right){
int mid = left + (right-left+1)/2;
if(nums[mid] > target){
right = mid - 1;
}else{
left = mid;
}
}
targetRight = right;
if(nums[targetLeft] != target){
return result;
}else if(nums[targetLeft] == nums[targetRight]){
result[0] = targetLeft;
result[1] = targetRight;
return result;
}else{
}
return result;
}
}三:搜索插入位置
class Solution {
public int searchInsert(int[] nums, int target) {
if(nums.length == 0){
return 0;
}
int targetLeft = 0 , n = nums.length;
int left = 0 , right = nums.length-1;
//这道题只用找一个左界限就够了
//左界限
left = 0 ; right = n-1;
while(left < right){
int mid = left + (right - left)/2;//左端点
if(nums[mid] >= target){
right = mid;
}else{
left = mid + 1;
}
}
targetLeft = left;
int result = 0;
if(target > nums[targetLeft]){
result = targetLeft + 1;
}else{
result = targetLeft ;
}
return result;
}
}四:x的平方根
class Solution {
public int mySqrt(int x) {
long left = 0 , right = x ;
if(x < 1 ){
return 0;
}
long mid = 0;//mid的平方越界了
while(left < right){
mid = left + (right - left + 1)/2;
if(mid * mid <= x){
left = mid;
}else{
right = mid - 1 ;
}
}
return (int)left;//强转为int类型
}
}
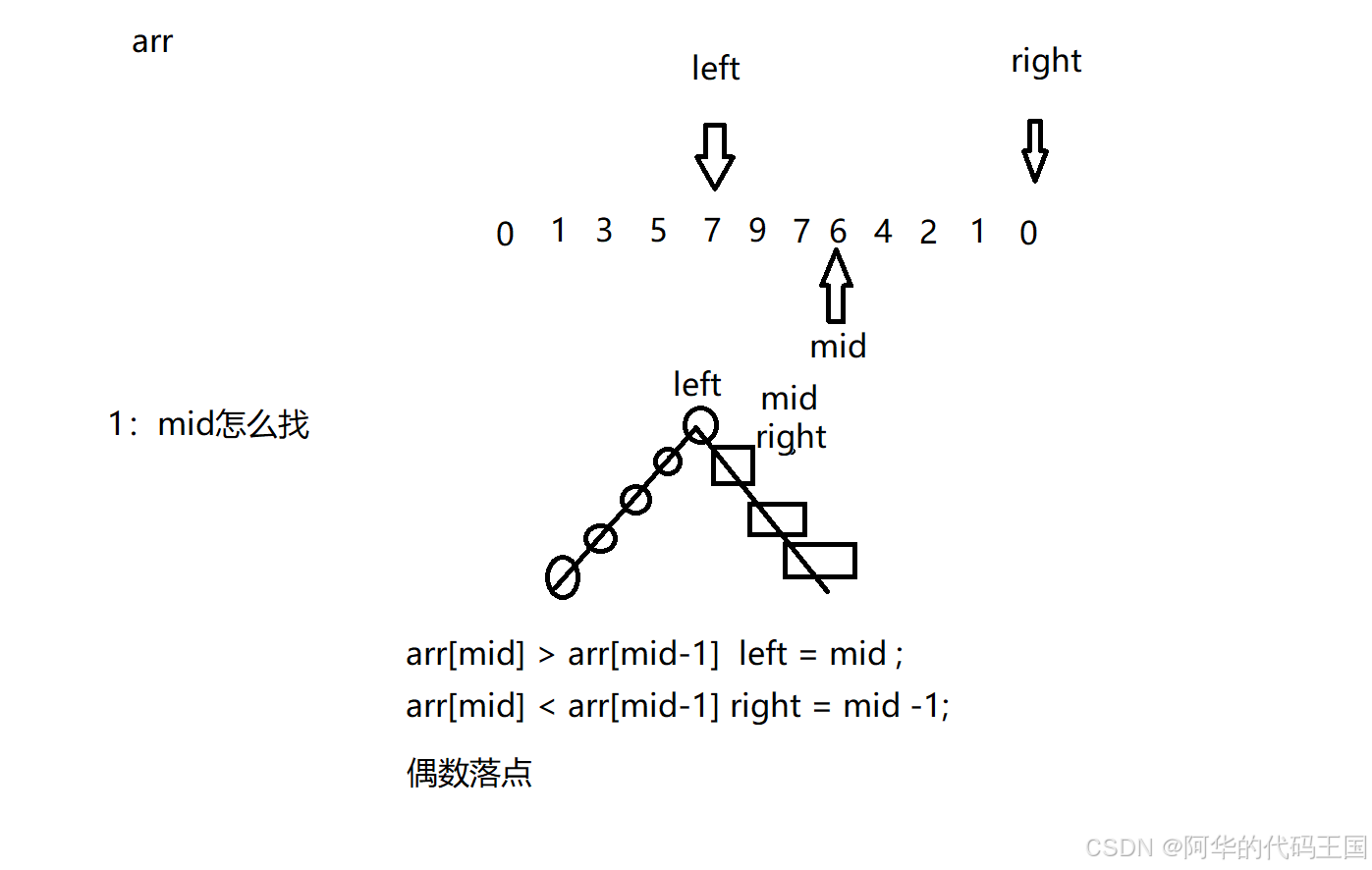
五:山脉数组的峰顶索引
class Solution {
public int peakIndexInMountainArray(int[] arr) {
int left = 0 , right = arr.length , n = arr.length;
while(left < right){
int mid = left + (right - left + 1)/2;
if(arr[mid] > arr[mid-1]){
left = mid;
}else if(arr[mid] < arr[mid-1]){
right = mid - 1;
}else{
}
}
return left;
}
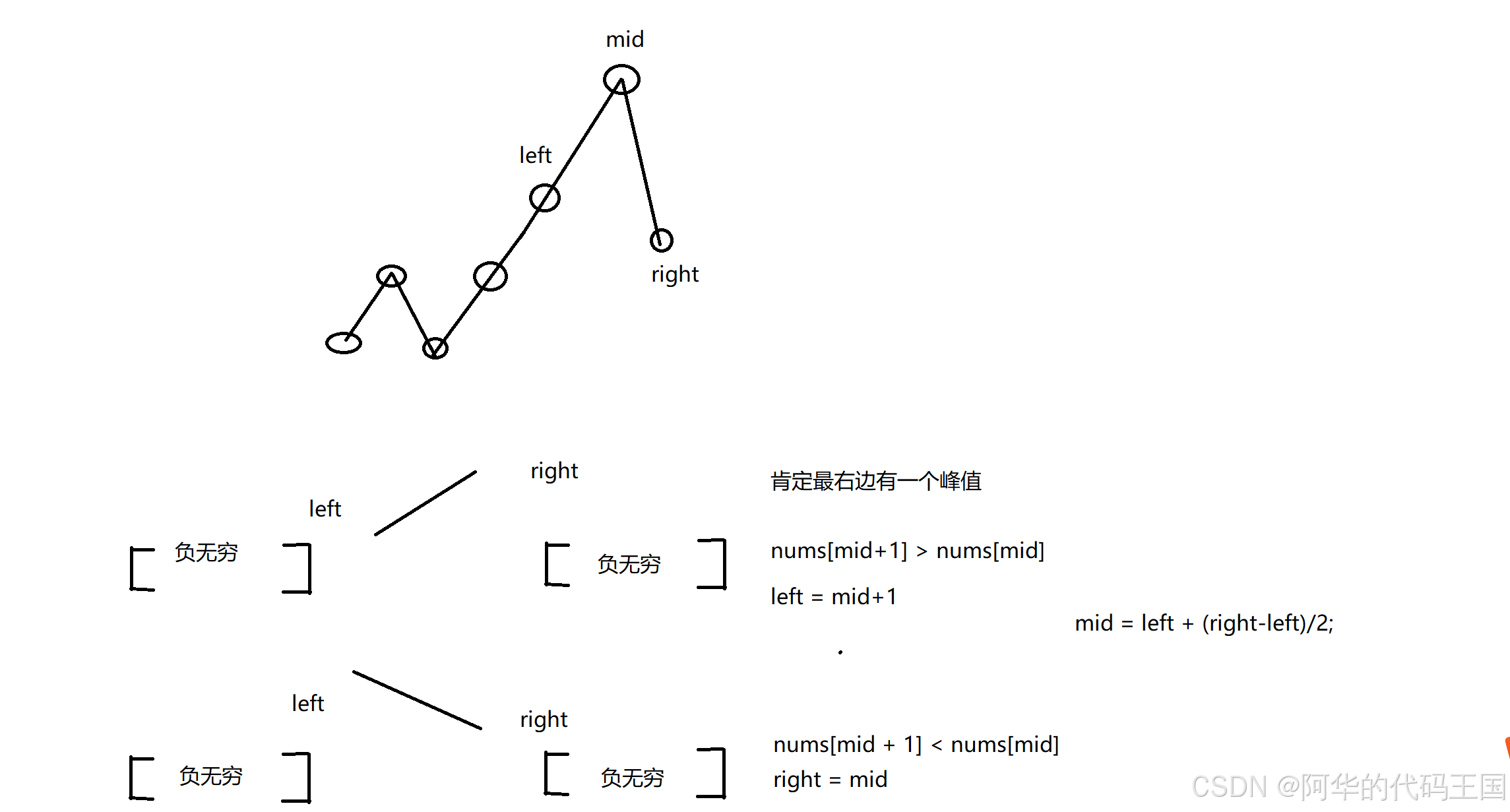
}六:寻找峰值
解法一
class Solution {
public int findPeakElement(int[] nums) {
int left = 0 , right = nums.length-1;
//如果数组中只有一个元素,while循环都进不去,规避了这个问题nb
while(left < right){
int mid = left + (right - left )/2;
if(nums[mid+1] > nums[mid]){
left = mid + 1;
}else if(nums[mid+1] < nums[mid]){
right = mid;
}else{
}
}
return left;
}
}
解法二
class Solution {
public int findPeakElement(int[] nums) {
//暴力解法
int n = nums.length , result = 0;
if(n == 1){
result = 0;
}else if(nums[0] > nums[1]){
result = 0;
}else if(nums[n-1] > nums[n-2]){
result = n-1;
}else{
int left = 0 , right = nums.length ;
while(left < right){
int mid = left + (right - left + 1)/2;
if(nums[mid] > nums[mid-1]){
left = mid;
}else if(nums[mid] < nums[mid-1]){
right = mid-1;
}else{
}
}
result = left;
}
return result;
}
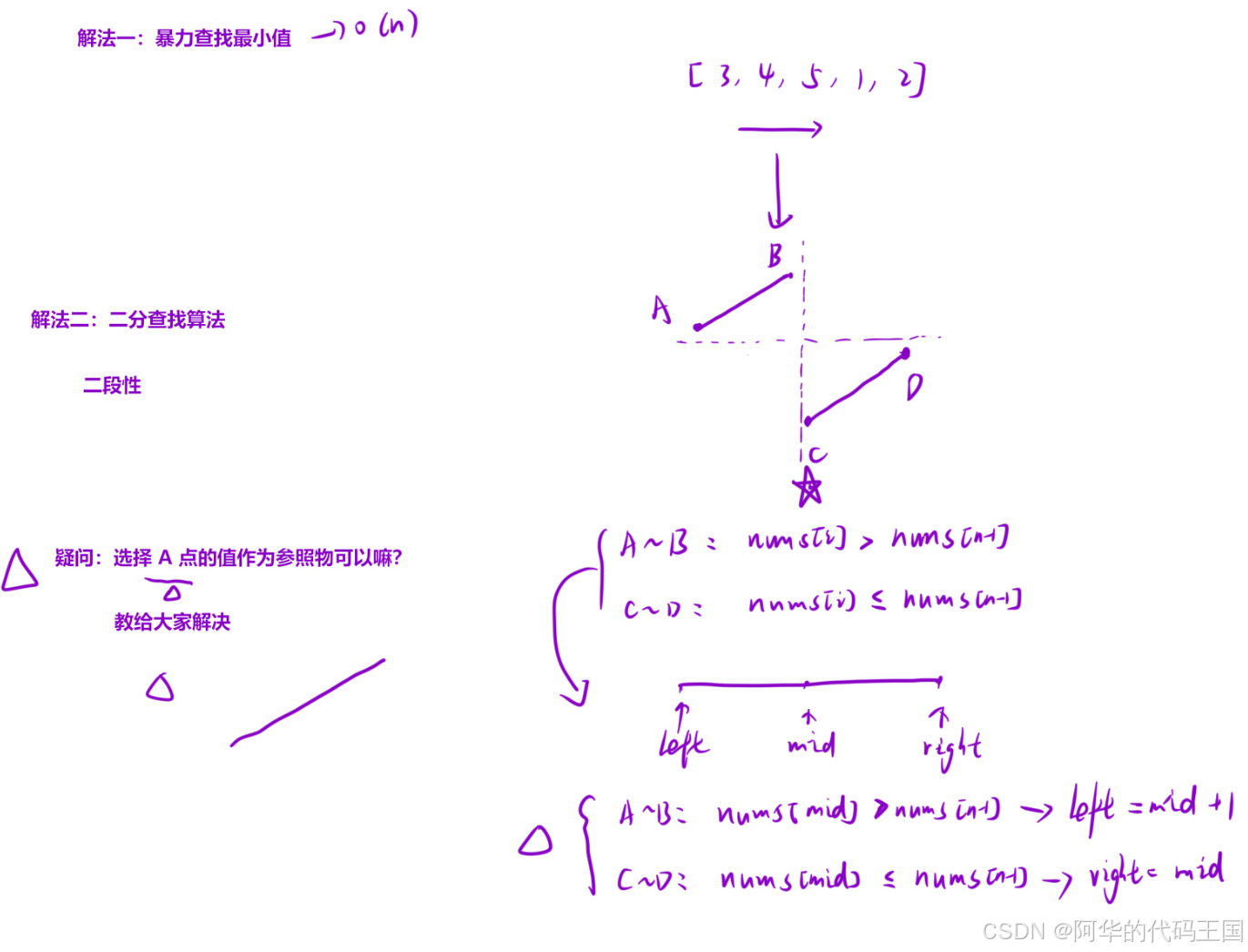
}七:寻找旋转排序数组中的最小值
class Solution {
public int findMin(int[] nums) {
int left = 0 , n = nums.length , right = n-1;
int tem = nums[n-1];
while(left < right){
int mid = left + (right - left)/2;
if(nums[mid] <= nums[n-1]){
right = mid;
}else{
left = mid + 1;
}
}
return nums[left];
}
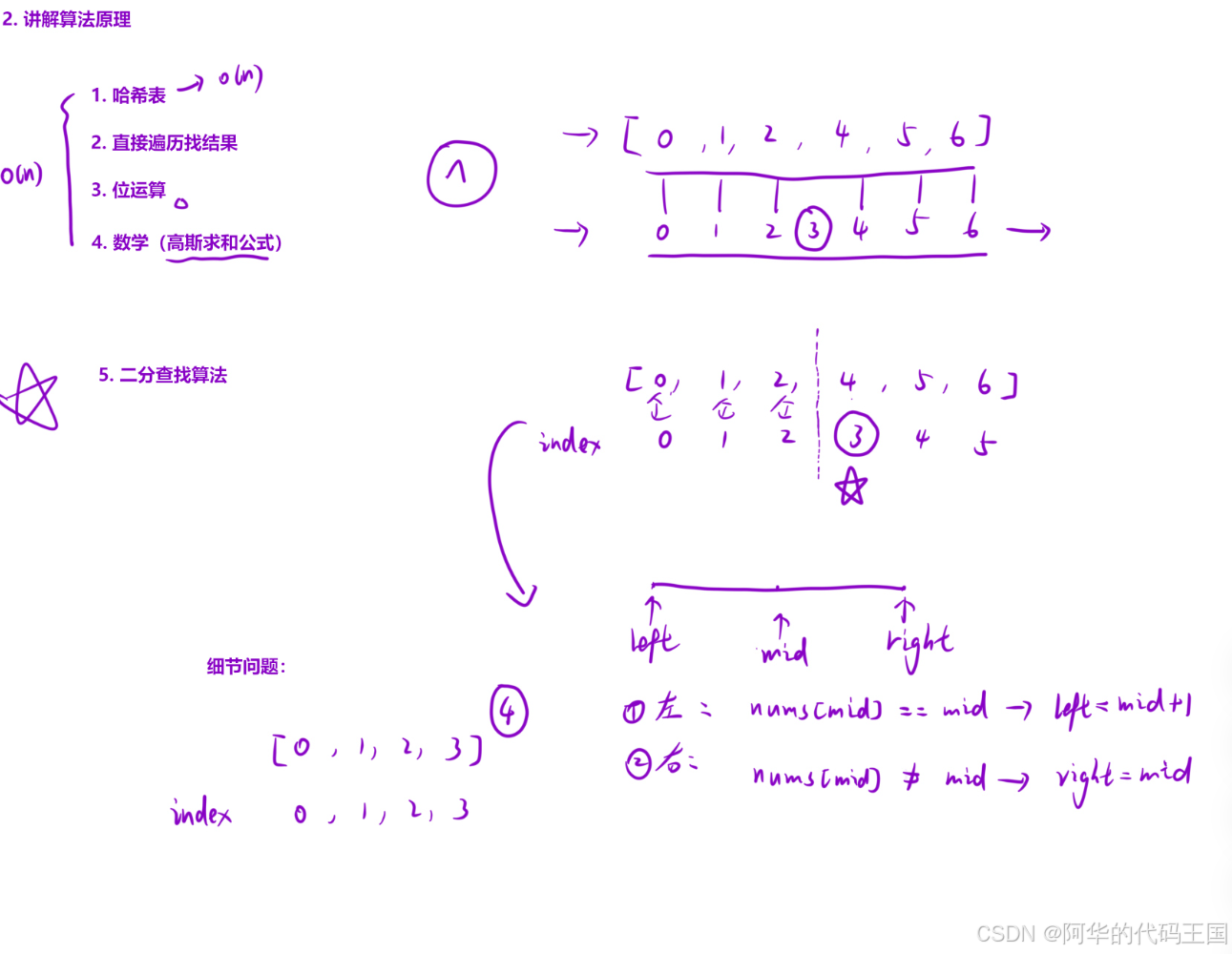
}七:点名
class Solution {
public int takeAttendance(int[] records) {
int left = 0 , n = records.length , right = records.length-1;
if(records[0] != 0){
return 0;
}
if(records[n-1] == n-1){
return n;
}
while(left < right){
int mid = left + (right - left)/2;
if(records[mid] - mid <= 0){
left = mid + 1;
}else{
right = mid ;
}
}
return right;
}
}