深入理解数据结构第六弹——排序（3）——归并排序

排序1：深入了解数据结构第四弹——排序（1）——插入排序和希尔排序-CSDN博客

排序2：深入理解数据结构第五弹——排序（2）——快速排序-CSDN博客

前言：

在前面，我们已经学习了插入排序、堆排序、快速排序等一系列排序，今天我们来讲解一下另一个很高效的排序方法——归并排序

一、归并排序的思想

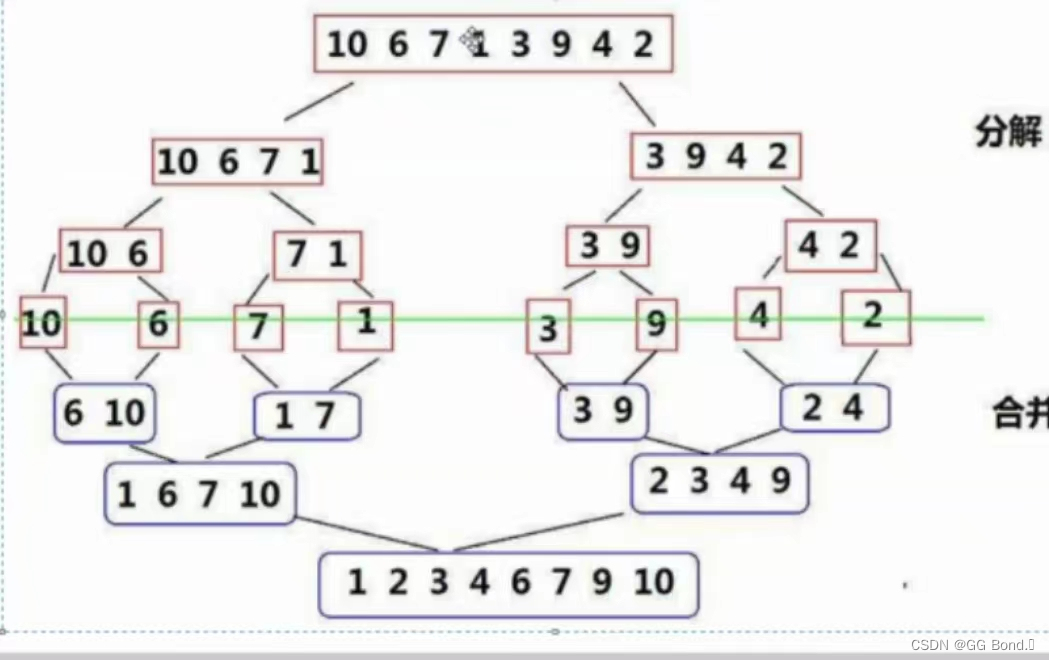
归并排序是一种经典的排序算法，它采用了分治法的思想。分治法的核心是“分而治之”，即将一个复杂的问题分解成两个或多个相同或相似的子问题，将这些子问题逐个解决，最后将子问题的解合并以解决原问题。

归并排序的基本思想如下：

分解（Divide）：

将待排序的数组从中间分成两半，递归地对这两半分别进行归并排序。
一直分解，直到每个子数组只包含一个元素，因为一个元素的数组自然是有序的。

解决（Conquer）：

当分解到最小子问题时，即每个子数组只有一个元素时，开始解决这些小问题。
解决的方式是合并（Merge）两个有序的子数组，从而得到一个更大的有序数组。

合并（Merge）：

合并过程是归并排序的关键步骤。它将两个有序的子数组合并成一个有序的数组。
通常使用两个指针分别指向两个子数组的起始位置，然后比较两个指针所指向的元素，将较小的元素放入结果数组中，并移动该指针。
重复这个过程，直到一个子数组被完全合并到结果数组中，然后将另一个子数组的剩余元素直接复制到结果数组中。

归并排序的操作如下：

归并操作其实就是将一组数据通过递归等不断划分成两个部分，直到划分到一个元素之后，再对这两部分排序排进一个数组内，相当于把划分的过程再反过来走了一遍，只是走回去的过程中会把数组一步一步的有序化

二、归并排序的递归实现

递归的实现其实是很有意思的，在上面我们已经讲了递归的思想，其实就是不断的重复划分然后排序的过程，所以我们就可以设计一个递归来实现这种，同时，由于每一步都要进行分区划分，所以我们可以封装一个划分函数（_MergeSort函数）在前，重复这个过程

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);

	_MergeSort(a, 0, n - 1,tmp);

	free(tmp);
}

1、因为我们在划分结束后，需要将各个小的部分再排序成一个有序的大部分，所以我们创建一个tmp的指针指向一个与原数组一样大小的空间，然后每一次排序放进这个空间，最后再把这个空间中的数据复制回原数组

2、其中_MergeSort函数内参数分别为原数组指针，首元素位置，尾元素位置，tmp指针

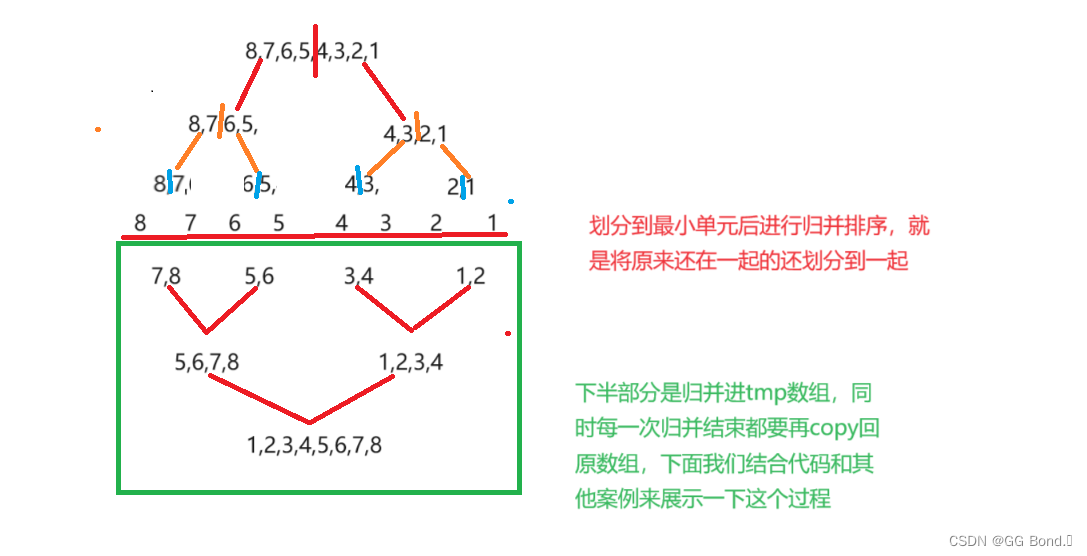
然后我们就来实现这个分步函数，这个函数的功能就是实现将一个数组不断分为两个部分，当划分成最小单元时，两个两个比较大小，并且放入tmp中，再复制进原数组中，我们先拿数组 { 8 ，7，6，5，4，3，2，1 } 举个例子

实现上述过程的代码如下

//归并排序
void _MergeSort(int* a, int begin,int end,int* tmp)
{
	if (begin == end)
		return;

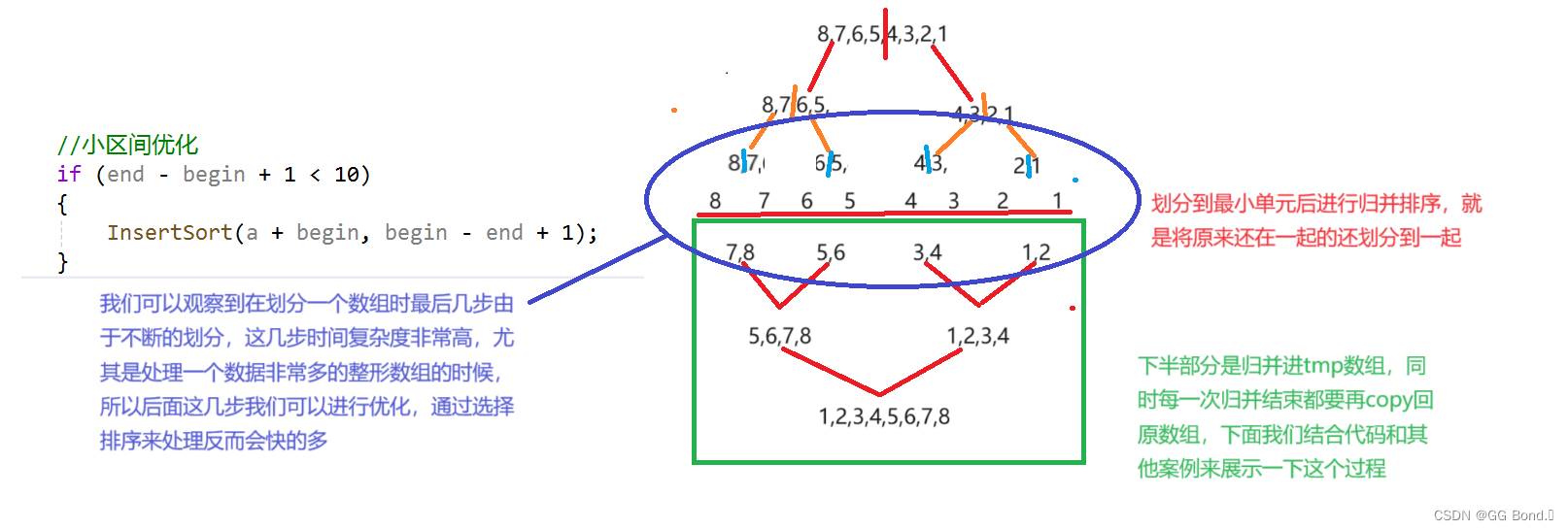
	//小区间优化
	if (end - begin + 1 < 10)
	{
		InsertSort(a + begin, begin - end + 1);
	}

	int mid = (begin + end) / 2;
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);
	
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1];
			begin1++;
		}
		else
			tmp[i++] = a[begin2++];
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

在这段代码有些部分我们在下面单独讲解一下：

小区间优化是什么及其作用

三、归并排序的非递归实现

学习完归并排序的递归实现后，我们来看一下归并排序的非递归实现

归并排序由于需要不断划分，可想而知其非递归实现是一定需要用到循环的，但是它其实还是有几个很大的坑等着我们的，归并排序的非递归实现要比其递归实现复杂的多

归并排序非递归实现需要注意的点：

1、在上面举的例子中我们都是举的2的n次方的例子，所以能恰好完全归并，但是我们实际排序时也可能遇到排11个数等，这里就比较麻烦了，所以我们需要分情况处理

2、由于上面在循环归并时次数的不确定性，所以我们每一次循环排序结束都要拷贝回原数组

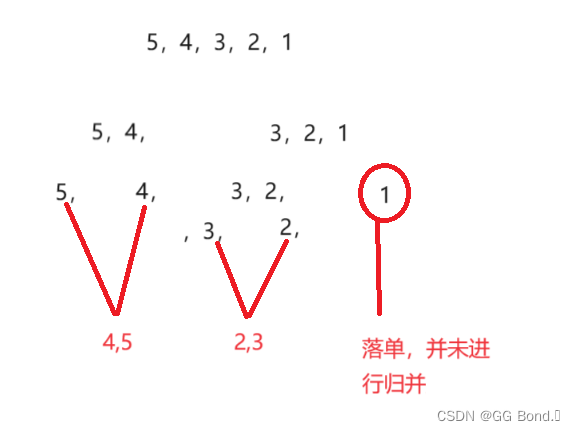
如图，我们在对两个数组进行归并时是要定义两个数组的起始位置的，但是我们可能会遇到下面三种情况：

1、end1>n，即从end1开始就超出数组长度

2、end1<n,begin2>n，即从begin2开始超出数组长度

3、end2>n，即从end2开始才超出数组长度

不管这上面哪一种，都会导致我们之后的归并排序中会有数组落单，所以我们就需要针对这中情况进行处理

针对这种情况我们有两种解决方法：

1、跳出：就是当end1或者begin2大于n时跳出不进行处理

2、优化：就是将end1、begin2、end2进行优化处理，让它能够进行操作

具体操作如下：

1、跳出的思想

//非递归的归并排序(跳出的思想）
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	int gap = 1;
	while (gap < n)
	{
		gap *= 2;
		int j = 0;
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + gap * 2 - 1;
			
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}
	}
	free(tmp);
}

2、优化的思想

//非递归的归并排序（修正的思路）
void MergeSortNonR2(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	int gap = 1;
	while (gap < n)
	{
		gap *= 2;
		int j = 0;
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + gap * 2 - 1;

			if (end1 >= n )
			{
				end1 = n - 1;
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}
	}
	free(tmp);
}

四、完整的代码实例

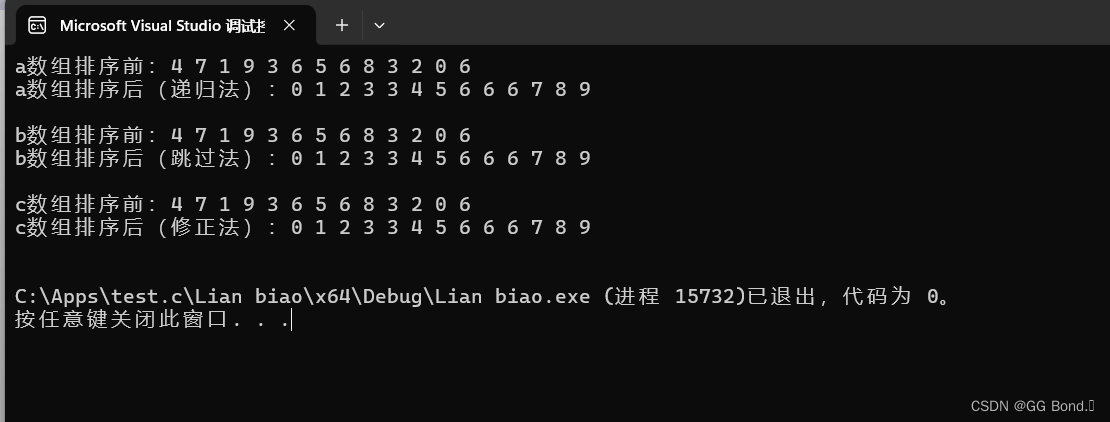
下面我们通过排序数组{ 4,7,1,9,3,6,5,6,8,3,2,0,6 }来检验这三种方法是否成功（递归一种，非递归i两种）

SeqList.h

#include<stdio.h>
//归并排序
void MergeSort(int* a, int n);

test.c

//测试归并排序
void TestMergeSort()
{
	int a[] = { 4,7,1,9,3,6,5,6,8,3,2,0,6 };
	int b[]= { 4,7,1,9,3,6,5,6,8,3,2,0,6 };
	int c[]= { 4,7,1,9,3,6,5,6,8,3,2,0,6 };
	printf("a数组排序前：");
	PrintArray(a, sizeof(a) / sizeof(a[0]));
	MergeSort(a, sizeof(a) / sizeof(a[0]));   //递归法
	printf("a数组排序后（递归法）：");
	PrintArray(a, sizeof(a) / sizeof(a[0]));
	printf("\n");

	printf("b数组排序前：");
	PrintArray(b, sizeof(b) / sizeof(b[0]));
	MergeSortNonR(b, sizeof(b) / sizeof(b[0]));   //非递归法(跳出法）
	printf("b数组排序后（跳过法）：");
	PrintArray(b, sizeof(b) / sizeof(b[0]));
	printf("\n");

	printf("c数组排序前：");
	PrintArray(c, sizeof(c) / sizeof(c[0]));
	MergeSortNonR2(c, sizeof(c) / sizeof(c[0]));   //非递归法（修正法）
	printf("c数组排序后（修正法）：");
	PrintArray(c, sizeof(c) / sizeof(c[0]));
	printf("\n");
}
int main()
{
	
	TestMergeSort();
	
	return 0;
}

SeqList.c

//归并排序
void _MergeSort(int* a, int begin,int end,int* tmp)
{
	if (begin == end)
		return;

	//小区间优化
	if (end - begin + 1 < 10)
	{
		InsertSort(a + begin, begin - end + 1);
	}

	int mid = (begin + end) / 2;
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);
	
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1];
			begin1++;
		}
		else
			tmp[i++] = a[begin2++];
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);

	_MergeSort(a, 0, n - 1,tmp);

	free(tmp);
}
//非递归的归并排序(跳出的思想）
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	int gap = 1;
	while (gap < n)
	{
		int j = 0;
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + gap * 2 - 1;
			
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}
		gap *= 2;

	}
	free(tmp);
}
//非递归的归并排序（修正的思路）
void MergeSortNonR2(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	int gap = 1;
	while (gap < n)
	{
		int j = 0;
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + gap * 2 - 1;

			if (end1 >= n )
			{
				end1 = n - 1;
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}
		gap *= 2;
	}
	free(tmp);
}
//打印数组
void PrintArray(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

程序运行结果：

五、总结

综合以上，我们其实就可以清楚的认识到归并排序的有趣及其思想，这篇文章并没有将归并排序的时间复杂度和适用场景等问题，我打算在后边写一个总结的文章，将这几种排序放在一起比较，给出他们时间复杂度的快慢和适用场景的不同，敬请期待吧！！！

谢谢各位大佬观看，创作不易，还请各位大佬点赞支持！！！