前缀和算法篇：解决子数组累加和问题

1.前缀和原理

那么在介绍前缀和的原理之前，那么我们先来说下前缀和最基本的一个应用场景，那么就是如我们标题所说的子数组累加和问题，那么假设我们现在有一个区间为[L,R]的数组，那么我们要求的其中子数组比如[L,i]或者[i,m] (L<=i<=m<=R)的累加和，那么我们最暴力的方法就是遍历一遍数组的子区间累加得到该子数组的累加和，那么我们每次求出一个累加和那么也就意味着要遍历一次数组，那么我们能否以一个较小的代价就能够得到子数组的累加和，那么这就是我们前缀和所应用的一个最基本的场景。

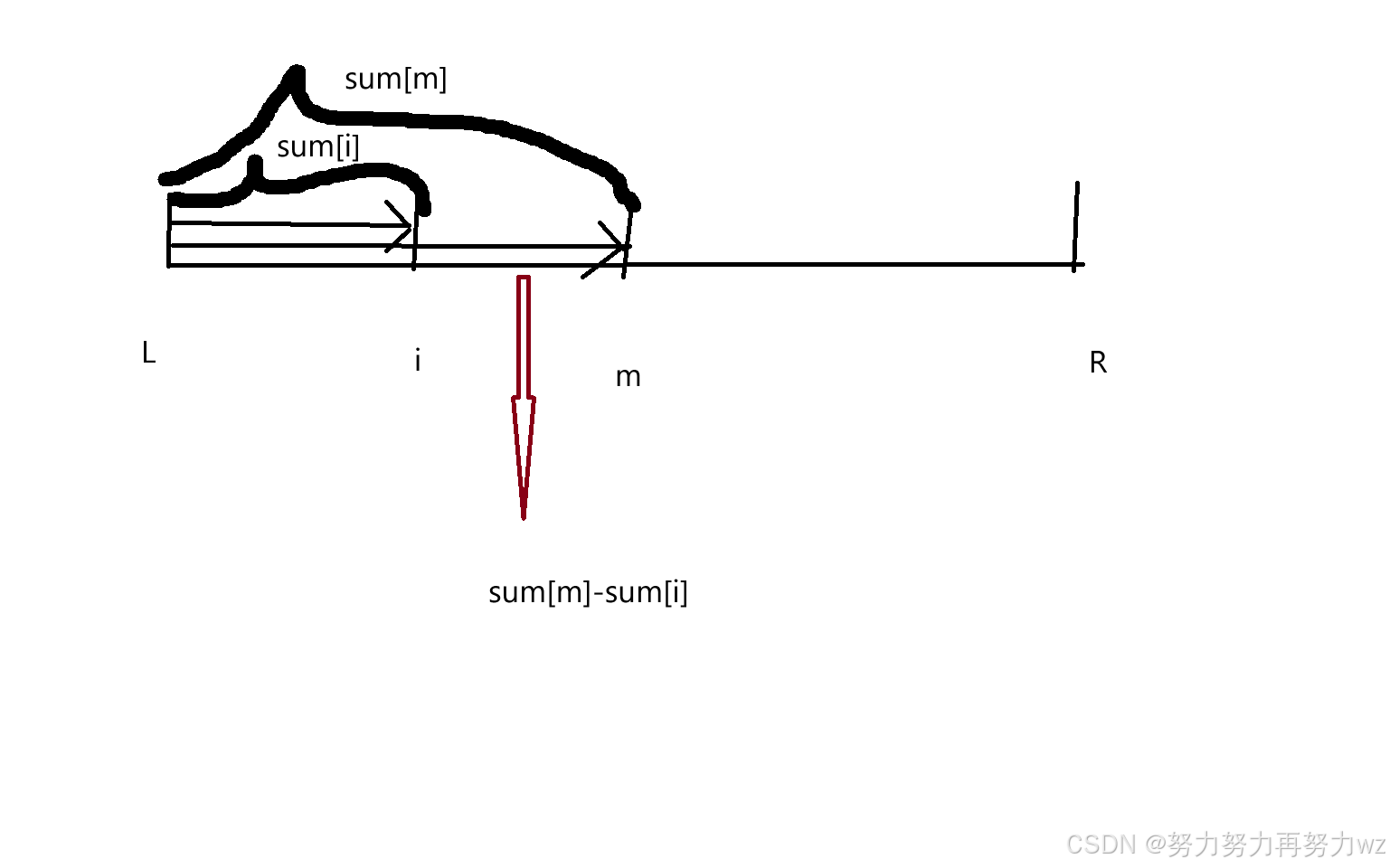
假设我们有了左边界L(或者说数组下标为0的位置)到这个数组中任意位置i的一个累加和，那么我们计算其中的子数组比如[i,m] (i<m)的累加和，那么我们只需要L到i的累加和sum1，以及L到m的累加和sum2，那么我们用sum2-sum1则是我们子数组[i.m]的累加和，那么这就是我们前缀和得到子数组累加和的一个原理

那么我们根据这个原理，如果我们加载一个前缀和数组sum，该数组的每一个的位置表示从左区间L到该位置的累加和，那么有了这个数组之后，我们可以计算区间[L,R]中任意一个子数组[i,m] (i<=m)的累加和假设其累加和为ant，那么公式则是ant=sum[m]-sum[i-1]。

所以现在的关键就是我们怎么得到前缀和数组，那么我们可以采取一个递推的思路加载我们的前缀和数组sum，那么最开始我们肯定只有左区间L到L的前缀和，它的前缀和就是数组下标为0的值，然后我们要扩展我们的前缀和L到1的前缀和，那么我们就通过前面计算好的L到L的前缀和加上arr[1]的值就是L到1，那么计算L到2，那么我们手上有计算好的L到1的前缀和，那么我们在这个L到1的前缀和的基础上加上arr[2]，那么同理现在要计算L到i位置，那么就用sum[i-1]+arr[i]即可，所以我们的代码实现可以采取一个循环的方式来得到我们的前缀和数组中的每一个位置的值。

但是这里我们知道我们计算[i,m] (i<=m)，我们公式是sum[m]-sum[i-1]，那么我们知道在数组中我们的左边界L就是为0，那么我们如果要计算[L,i]的累加和的话，那么公式就是sum[i]-sum[L-1]，而这里L是0，那么L-1就是-1，可是对于数组来说，访问不到下标为-1的前缀和数组，所以这里为了处理边界，我们会将区间[L,R]整体往右平移一个单位[L+1,R+1],也就是说在加载我们的前缀和数组的时候，我们理解为我们的原数的数组内容的开头的左侧多出了一个0，然后再加载我们的前缀和数组，这样[L,i]的累加和就是sum[i+1]-sum[L]

代码模版：

#include<iostream>
#include<vector>
using namespace std;
#define N 8
int main()
{
	vector<int> arr={0,1,2,3,4,5,6};
	vector<int> sum(N,0);
	for(int i=1;i<sum.size();i++)
	{
		sum[i]=sum[i-1]+arr[i-1];
	}
	return 0;
}

2.前缀和应用

题目一：求子数组累加和 难度：EZ

题目：现在给你一个数组，数组中的元素有正有负，让你求其中区间为[L,R]的子数组的累加和。

题目思路：那么这个题就是我们上文所说的前缀和最基本的应用场景，纯纯模版题，那么就套我们的模版来做即可

代码实现：

class solution
{
	int count(vector<int>& arr,int l,int r)
	{
		 vector<int> sum(arr.size()+1,0);
		 for(int i=1;i<sum.size();i++)
		 {
		 	sum[i]=sum[i-1]+arr[i-1];
		 }
		 return sum[r+1]-sum[l];
	}
}

题目二：求累加和为aim的最长子数组 难度：MID

题目：现在给一个数组，数组中的元素有正有负，那么我们要求这个数组中累加和为aim，并且最长的子数组，返回这个最长子数组的长度。

题目思路：那么这里我们要求累加和为aim且长度最长的子数组，那么这里我们看到有关于子数组问题的，那么一定就要敏感，因为子数组意味着连续区间，那么它可以应用我们的滑动窗口或者前缀和，但是具体题目得具体分析。

那么这里我们可以这样想，假设我们这个数组的整体的区间为[L,R],那么我们就求这个区间上每一个位置i，求以该位置作为子数组结尾往左延伸的并且累加和为aim的子数组的最长长度，那么我们有了每一个位置以该位置结尾的子数组的最长长度，那么我们在综合每一个位置的长度得到最长的，那么这个最长的长度就是我们整个区间[L,R]所能够得到的累加和为aim的最长子数组长度。

那么现在问题就变为了我们怎么求每个位置的以该位置结尾的累加和为aim的最长子数组呢？那么我们可以首先加载一个该数组的前缀和数组，那么我们对于每一个L到i位置区间的前缀和，我们可以以该视角去理解该区间的前缀和

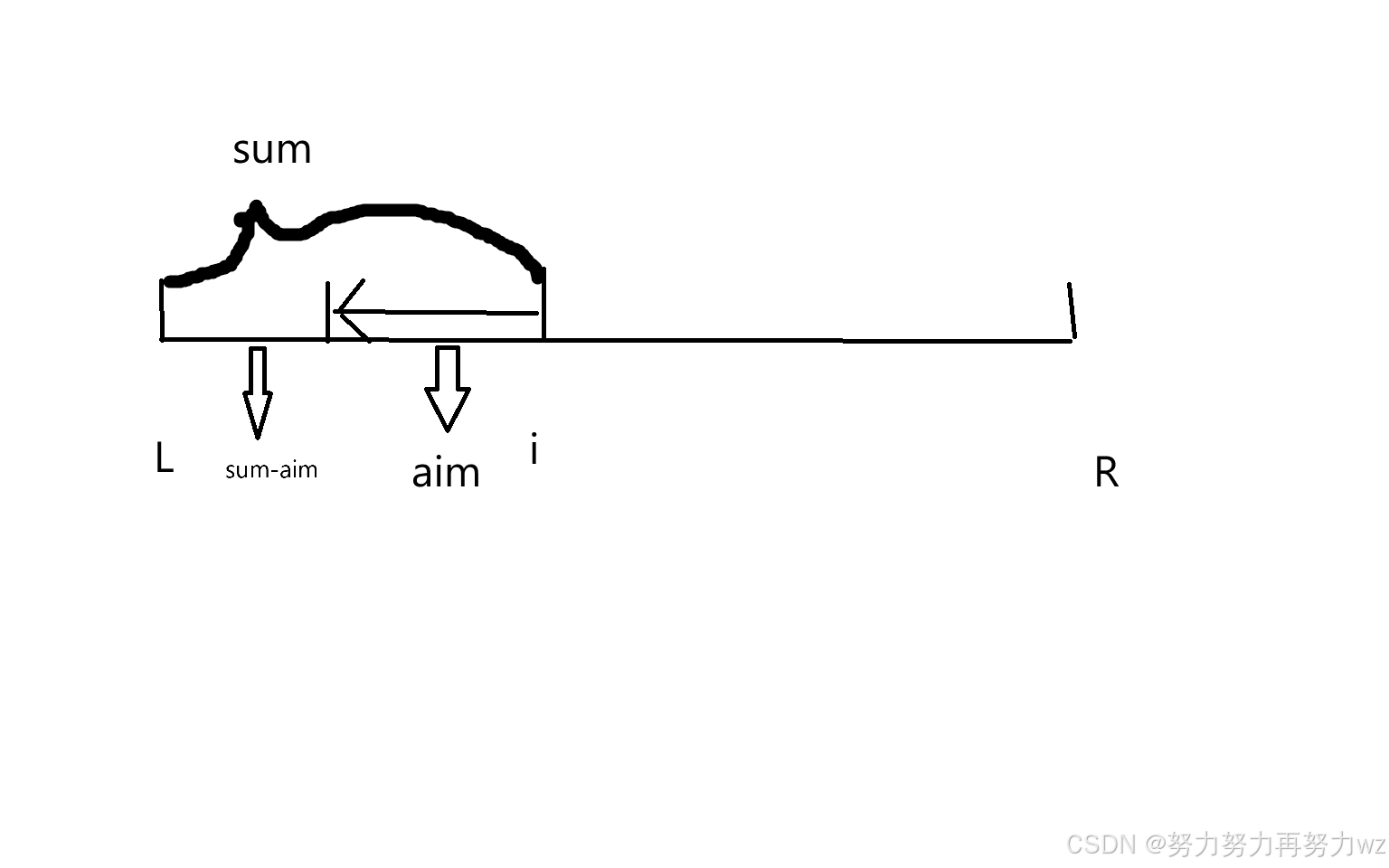
我们假设我们L到i位置区间的前缀和为sum，那么我们这里的sum前缀和可以由两部分得到，假设我们在这个L到i位置区间任取一个点位m，那么我们这里L到i区间的前缀和可以等价于L到m位置的前缀和加上我们的m到i位置累加和得到，那么我们按照这个理解的话，那么求以这个数组中任意以i位置结尾往左延伸的累加和为aim的子数组，我们可以看成我们L到i区间的前缀和sum是由以该i位置结尾往左延伸到m位置的累加和aim加上L到m的前缀和sum-aim得到，那么我们要往左延伸的更长，那么意味着我们的前缀和sum-aim的长度就得更短，那么所谓更短就是我们这个前缀和sum-aim出现的位置更靠前，那么我们就可以从左往右加载我们的前缀和数组的时候同时通过一个哈希表其中可以是前缀和，value值是该前缀和第一次出现从左侧第一次出现的位置，那么这个位置就是我们sum-aim最靠前的位置

那么由于我们是在加载我们前缀和的同时，计算好我们当前i位置的前缀和后如果是以第一次出现的话立马会添加进哈希表当中计算好i位置的前缀和，那么我由于我们是从左往右加载我们的前缀和同事将计算好的前缀和添加到哈希表中，那么也就意味着我们此时在哈希表中记录的第一次出现的前缀和的位置一定是在i位置的左侧而不是右侧，因为我们还未计算i位置右侧的前缀和，所以我们计算好i位置的前缀和，然后立马查询哈希表计算出该位置往左延伸累加和为aim的最长子数组，然后在每个位置综合得到整个区间累加和为aim的最长子数组。

代码实现：

class Solution
{
public:
    // 计算数组中累加和为aim的最长子数组的长度
    int count(vector<int>& arr, int aim)
    {
        vector<int> sum(arr.size() + 1, 0); // 前缀和数组，大小比原数组多1
        int ans = 0; // 存储最长子数组的长度
        unordered_map<int, int> value; // 哈希表，存储前缀和及其首次出现的索引
        value[0] = 0; // 初始化哈希表，前缀和为0时的索引为0

        for (int i = 1; i < sum.size(); i++)
        {
            sum[i] = sum[i - 1] + arr[i - 1]; // 计算前缀和

            // 如果当前前缀和已经存在于哈希表中，更新其索引为最新位置
            // 但实际上，我们不需要更新，因为我们只关心第一次出现的位置
            // 检查是否存在前缀和为sum[i] - aim的索引
            if (value.find(sum[i] - aim) != value.end())
            {
                // 如果存在，计算当前子数组的长度，并更新最长长度
                ans = max(ans, i - value[sum[i] - aim]);
            }

            // 如果当前前缀和不在哈希表中，则添加进去
            if (value.find(sum[i]) == value.end())
            {
                value[sum[i]] = i;
            }
        }

        return ans;
    }
};

题目三：求子数组累加和为aim的个数 难度：MID

题目：现在我们有一个数组，那么我们要求这个数组中子数组累加和为aim的个数。

题目思路：那么在上一个题目，我们就说了，我们一个区间为[L,R]的一个数组的累加和假设为sum，那么它的累加和可以看做我们前缀和L到i位置的累加和加上i到R位置的累加和，那么这里我们的思路就是求这个数组中每个位置结尾往左延伸累加和为aim的数量，然后累加每个位置得到以该位置结尾的累加和为aim的数量就是我们整个数组累加和为aim的子数组的数量。

那么我们求每个位置i以该位置结尾的累加和为aim的数量，那么我们知道L到i区间的前缀和sum可以看做由L到m位置的前缀和加上m到R位置的前缀和，那么我们这里统计我们在L到i位置处的前缀和为sum-aim的数量有多少个，那么就可以得到以i位置为结尾的累加和为aim的子数组有多少个

那么我们实现则是在加载前缀和的同时记录我们的哈希表，我们哈希表则记录前缀和出现的次数，那么我们在从左往右加载我们前缀和数组的同时，然后计算该位置处的累加和为aim的子数组的数量，因为我们是从左往右遍历数组，然后更新我们的哈希表，那么此时记录在哈希白中的各种前缀和出现的次数一定都是在i位置之前的，因为i位置之后的前缀和我们还未被记录到哈希表当中去，所以我们边加载我们的前缀和数组，边查询我们的哈希表得到每个位置以该位置结尾的累加和为aim的子数组的数量

代码实现:

class Solution
{
public:
    // 计算数组中子数组累加和为aim的个数
    int count(vector<int>& arr, int aim)
    {
        vector<int> sum(arr.size() + 1, 0); // 前缀和数组，大小比原数组多1
        int ans = 0; // 存储满足条件的子数组个数
        unordered_map<int, int> value; // 哈希表，存储前缀和及其出现次数
        value[0]++; // 初始化哈希表，前缀和为0的初始出现次数为1

        for (int i = 1; i < sum.size(); i++)
        {
            sum[i] = sum[i - 1] + arr[i - 1]; // 计算当前位置的前缀和

            // 在更新哈希表之前，先查询是否存在前缀和为sum[i] - aim
            // 如果存在，说明从某个位置到当前i位置的子数组累加和为aim
            ans += value[sum[i] - aim];

            // 更新哈希表中当前前缀和的出现次数
            value[sum[i]]++;
        }

        return ans;
    }
};

题目四：求正负数相等的子数组的最大长度 难度：MID

题目：我们现在会有一个数组，那么这个数组的元素包含正负数以及零，那么我们要求求出满足正数的数量与负数的数量相等的子数组的最长长度。(注：这里只关心正数与负数是否相等，不算数值0哦)

例：[12,-1,-6,0,3,6]

其中最长子数组是区间为[0,4]的子数组[12,-1,-6,0,3]以及区间[1,5]的子数组[-1,-6,0,3,6]，长度都为5

题目思路：那么这里我们分析题意，那么这里我们只要寻找正数以及负数数量相等的子数组，那么这道题的关键就是我们不关心这个数组中各个数的数值而只关心该数的一个状态是正数还是负数还是0，所以我们就得将我们的原数组首先给预处理一下，我们原数组的各个数值的正数比如12或者6，那么在这道题中无论他的数值在大或者在小，那么他们都是同一类数，也就是正数，所以我们预处理得到的数组只有这个数的状态信息没有数值信息，所以我们这里将我们的正数转换为1，负数转换为-1,0就是0，比如原数组为[12,-1,-6,0,3,6]，那么经过预处理之后得到数组是[1,-1,-1,0,1,1]，那么我们接着对预处理数组加载一个前缀和数组

那么该对于区间[L,R]的数组来说，如果该位置i的前缀和为0，那么说明该区间的正负数的数量相等，整个区间就记录答案，，若位置i的前缀和不为0，那么说明这个区间[L,i]中的数的分布是负数是不等于正数的，那么也就是说我们该区间中还有可能有正负数的数量相等的区间存在，因为我们知道一个区间[L,R]的前缀和可以由区间[L,m]的前缀和加上[m,R]的前缀和，所以我们这里的思路就是求每个位置以该位置为结尾往左延伸满足正数的数量等于负数的数量的最长子数组，那么最后我们求得每个位置满足要求的最长长度，那么综合就得到整个区间满足要求的最长子数组长度

所以这里如果我们的i位置的前缀和不为0，假设i位置的前缀和为sum，那么我们找在i位置之前的前缀和为sum出现的最靠前的位置，因为sum+0=sum，那么找到i位置之前最靠前的sum位置m，那么m到i的累加和就是0，那么就是以i位置结尾往左延伸的正负数数量相等的最长子数组

所以我们在加载我们的前缀和数组的时候同时将每个前缀和第一次出现的位置记录在我们的哈希表，那么我们在加载计算出我们该i位置的前缀和的同时，那么我们查询我们的哈希表，那么此时哈希白记录的是前缀和第一次出现的位置，由于我们是从左往右加载前缀和数组的同时查询我们的哈希表，那么我们这里i位置右侧位置的前缀和都还未被计算添加哈希表中，所以意味着我们在哈希表当中记录的第一次出现的前缀和都是在i位置的左侧的，所以我们就可以查询得到我们以i位置结尾的满足要求的最长子数组，综合每个位置得到答案，那么该题经过预处理之后就和第二题是一样的了。

代码实现：

class Solution
{
public:
    int count(vector<int>& arr)
    {
        // 预处理数组，将正数转为1，负数转为-1，零保持为0
        for (int i = 0; i < arr.size(); i++)
        {
            if (arr[i] > 0)
            {
                arr[i] = 1;
            }
            else if (arr[i] < 0)
            {
                arr[i] = -1;
            }
            // 零保持为0，不需要显式处理
        }

        vector<int> sum(arr.size() + 1, 0); // 前缀和数组，大小比原数组多1
        int ans = 0; // 存储最长子数组长度
        unordered_map<int, int> value; // 哈希表，存储前缀和及其首次出现的位置
        value[0] = 0; // 初始化，前缀和为0的初始位置为0

        for (int i = 1; i < sum.size(); i++)
        {
            sum[i] = sum[i - 1] + arr[i - 1]; // 计算当前位置的前缀和

            // 如果当前前缀和已经在哈希表中，则更新最长子数组长度
            // 如果 sum[i] 已经存在，则不更新 value[sum[i]]，以保持最左边的位置
            if (value.find(sum[i]) == value.end())
            {
                value[sum[i]] = i; // 记录前缀和首次出现的位置
            }

            // 检查是否存在前缀和为 -sum[i]，即 sum[i] + (-sum[i]) = 0
            // 这意味着从 value[-sum[i]] 到 i 的子数组满足条件
            if (value.find(-sum[i]) != value.end())
            {
                ans = max(ans, i - value[-sum[i]]);
            }
        }

        return ans;
    }
};

题目五：求表现良好的最长时间段 难度：MID

题目：那么这里我们会给一个数组，数组的每一个元素代表着员工当天工作一个时间，数值都是非负数，那么如果当天工作时间大于8小时的话就是疲劳的一天，如果小于等于8就是精神良好的一天，那么良好的时间段就是在该时间段内精神良好的一天的数量大于疲劳的一天的数量，求良好时间段的最长长度是多少。(注：时间段必须是连续的)

例：[10,10,10,9,1,1]

表现良好的最长时间段是[9,1,1]，长度是3

题目思路：那么这道题的话，还是跟上一道题一样，那么这里我们不同数值的数中共就可以分为两个状态，分别是疲劳以及精神良好，那么我们还是得预处理我们的数组，将大于8的数转换为-1，小于等于8的数转换为1

那么对于任意位置i来说，如果该位置的前缀和大于等于1，那么说明在L到i这个区间中数的分布是正数大于负数，那么整个区间就到达标，那么如果说我们的前缀和是小于等于0的，那么说明负数的数量是大于等于我们的正数的，那么这个区间是有正数的数量大于负数的数量的可能的，那么这里假设i位置的前缀和为sum，那么找到sum-1出现的最早位置即可

那么假设i位置的前缀和是-3，那么我们要在的则是-4出现的最早位置，那么这里就会产生一个疑问为什么不找我们-5以及-6前缀和出现的最早位置呢，那么这里就是本题目的一个难点，**我们知道我们经过预处理之后的数组的数值只有1和-1两种，所以一个前缀和只能一点一点的增加和减少，所以要得到我们的前缀和-5，那么它一定是在它之前有一个右侧前缀和为-4在其右侧加了一个累加和为-1的区间才能达到前缀为-5，那么同理要得到前缀和为-6，那么得到-6之前也得有一个前缀和为-5在其右侧要加一个累加和为-1的区间，那么也就意味这我们我们最早出现前缀和为-5的区间一定是在最早出现前缀和为-4的区间的右侧，同理最早出现前缀和为-6的区间一定出现在最早出现的前缀和为-5的区间的右侧，**那么我们现在只需要以i位置为结尾往左延伸的正数数量大于负数数量的最长子数组，那么该最长子数组的累加和一定是大于等于1，那么我们就只需要找到sum-1的前缀和出现的最早位置，在我们刚才的例子中，i位置的前缀和为-3，那么我们找前缀和为-4出现的最早位置，那么至于这么找前面的题我们已经说了用我们的哈希表，那么这里我就不再赘述了，直到把刚才加粗的内容想通，那么这个题的难点就被解决了。

代码实现：

class Solution {
public:
    int longestGoodPeriod(vector<int>& hours) {
        // 预处理数组，将大于8小时的工作时间转换为-1，小于等于8小时的工作时间转换为1
        vector<int> transformed(hours.size());
        for (int i = 0; i < hours.size(); ++i) {
            transformed[i] = (hours[i] > 8) ? -1 : 1;
        }

        // 前缀和数组
        vector<int> prefixSum(transformed.size() + 1, 0);
        for (int i = 1; i <= transformed.size(); ++i) {
            prefixSum[i] = prefixSum[i - 1] + transformed[i - 1];
        }

        // 哈希表，存储每个前缀和首次出现的位置
        unordered_map<int, int> prefixSumIndex;
        prefixSumIndex[0] = 0; // 初始化，前缀和为0的初始位置为0

        int maxLength = 0;

        // 遍历前缀和数组，寻找满足条件的最长子数组
        for (int i = 1; i <= transformed.size(); ++i) {
            int currentSum = prefixSum[i];

            // 如果当前前缀和减1存在于哈希表中，则计算子数组长度
            if (prefixSumIndex.find(currentSum - 1) != prefixSumIndex.end()) {
                int startIndex = prefixSumIndex[currentSum - 1];
                maxLength = max(maxLength, i - startIndex);
            }

            // 如果当前前缀和还未出现在哈希表中，则记录其首次出现的位置
            if (prefixSumIndex.find(currentSum) == prefixSumIndex.end()) {
                prefixSumIndex[currentSum] = i;
            }
        }

        return maxLength;
    }
};

3.结语

那么这就是本篇文章关于前缀和的所有内容，那么讲了前缀和的原理以及代码实现，还有具体的应用，那么我们知道与子数组有关的问题，那么我们可以先往前缀和方向上思考，看能不能应用。

那么如果这篇文章让你有所收获的话，那么就三连关注支持一下博主，那么我们会持续更新，请大家多多关注与支持！