目录
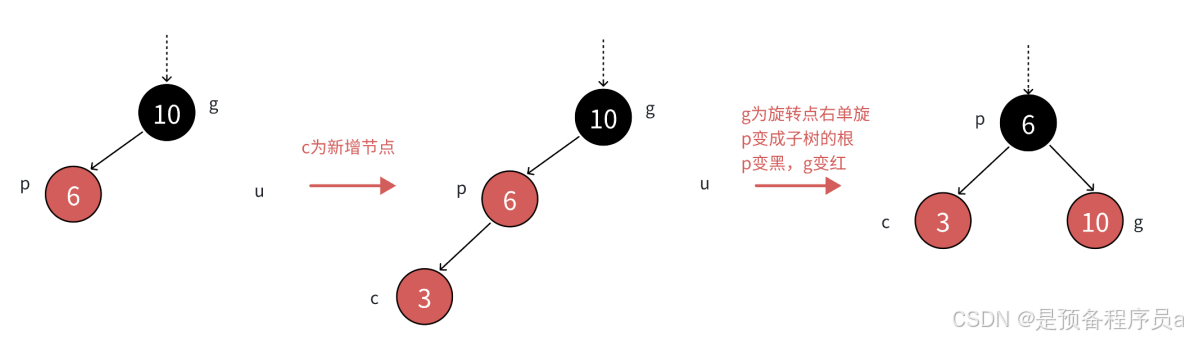
2.2.1.1 u(uncle)不存在 ,c为p的左孩子(单旋+变色)
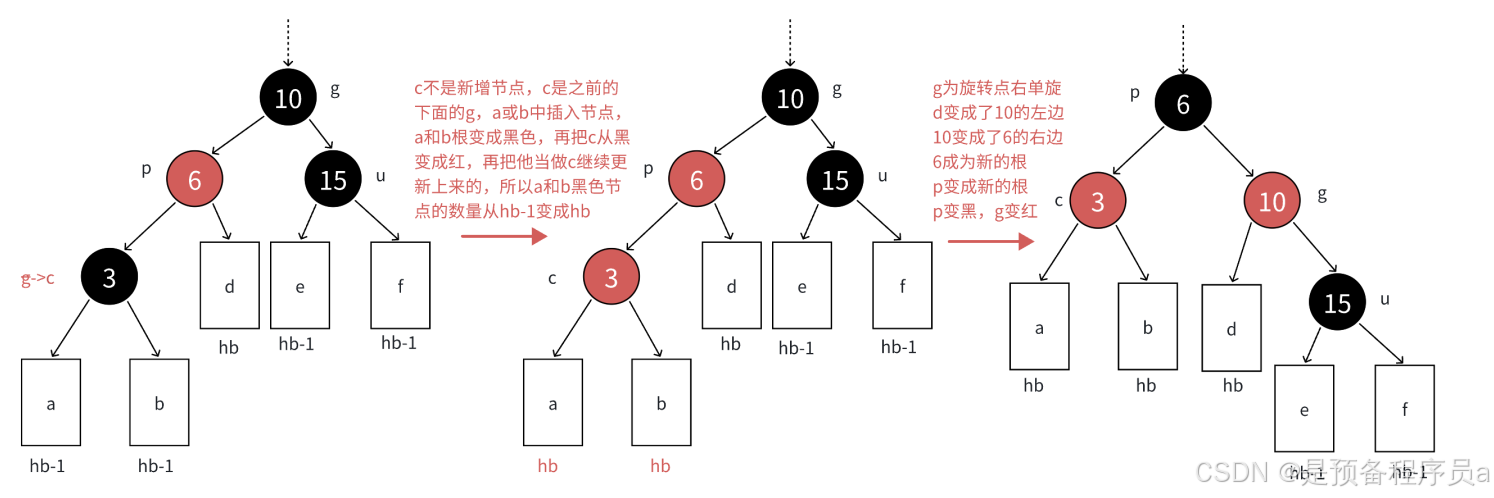
2.2.1.2 uncle存在且为黑,c为p的左孩子(单旋+变色)
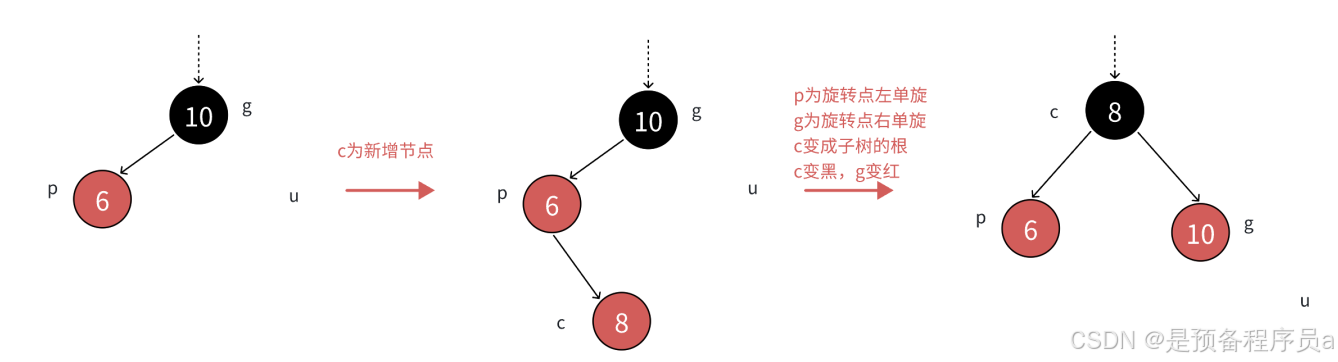
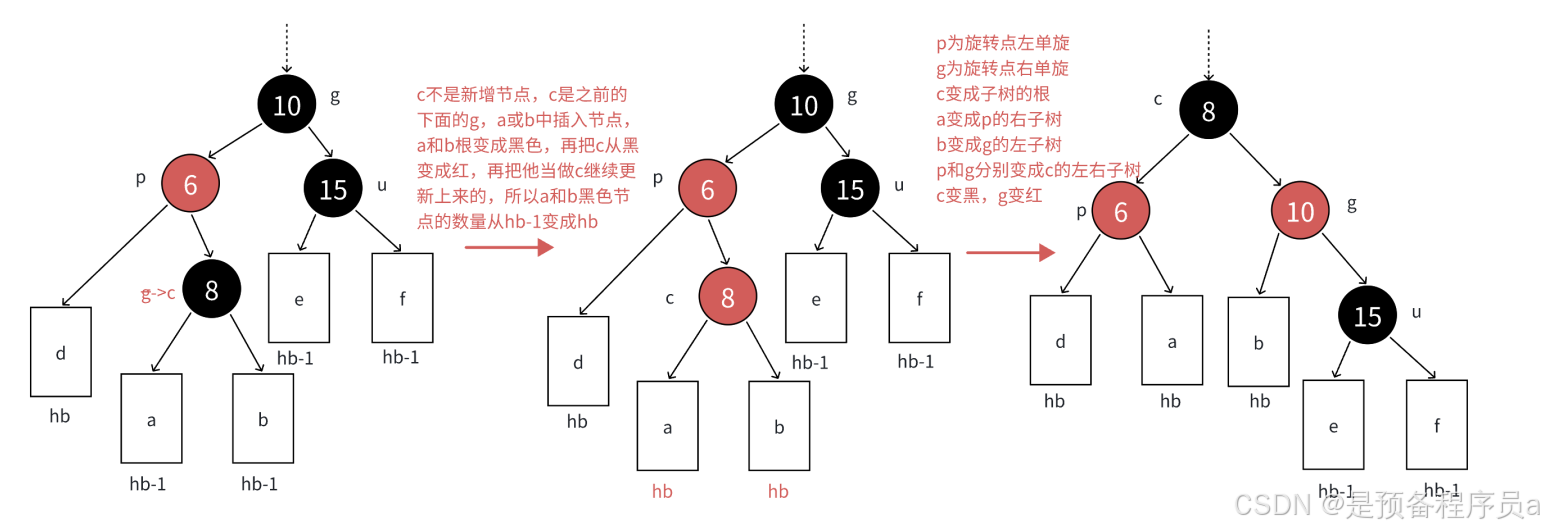
2.2.1.3 u(uncle)不存在 ,c为p的右孩子(双旋+变色)
1.红黑树的概念
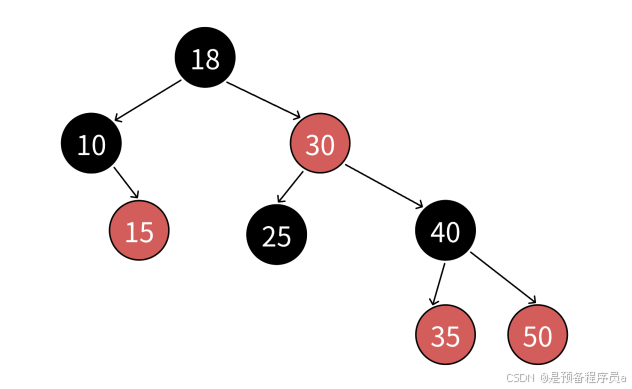
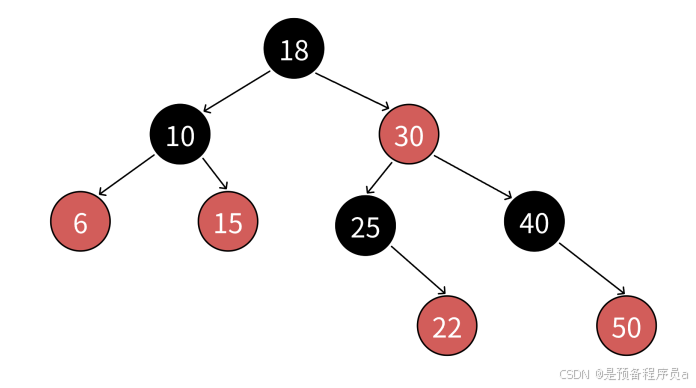
红黑树是一棵二叉搜索树,但是在此基础之上,又增加了一个存储为来表示节点的颜色,可以是红色或者是黑色。通过对任意一条根到叶子的路径上的各个节点的颜色来进行约束,红⿊树确保没有⼀条路径会⽐其他路径⻓出2倍,因⽽是接近平衡的。
1.1红黑树的规则
1.每个结点不是红⾊就是⿊⾊。
2.根结点是⿊⾊的。
3.如果⼀个结点是红⾊的,则它的两个孩⼦结点必须是⿊⾊的,也就是说任意⼀条路径不会有连续的红⾊结点。
4. 对于任意⼀个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的⿊⾊结点。
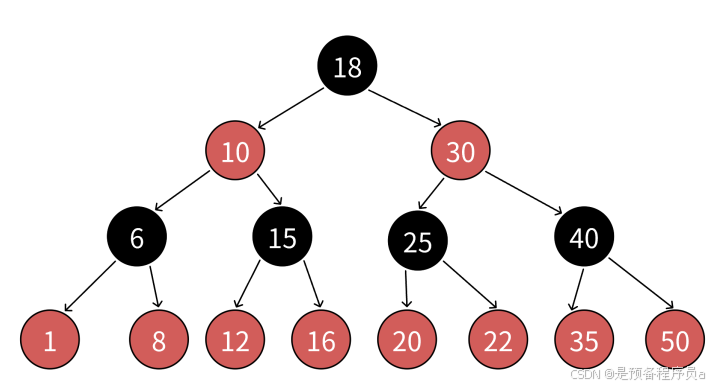
(则说明,假设一条路径有n个黑节点,且全为黑,没有红,则该条路径最短;则最长路径肯定是一黑一红交替出现,因为红节点不能连续出现,所以最长路径节点数是2n。!!最短路径和最长路劲不一定存在,我这里只是做一个讲解。)
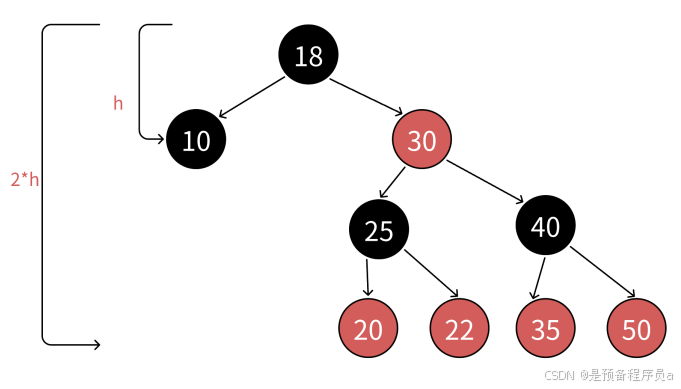
1.2红黑树的效率
假设N是红⿊树树中结点数量,h最短路径的⻓度,那么 2h − 1 <= N < 22∗h − 1 , 由此推出
h ≈ logN ,也就是意味着红⿊树增删查改最坏也就是⾛最⻓路径 2 ∗ logN ,那么时间复杂度还是
O(logN ) 。
红⿊树的表达相对AVL树要抽象⼀些,AVL树通过⾼度差直观的控制了平衡。红⿊树通过4条规则的颜⾊约束,间接的实现了近似平衡,他们效率都是同⼀档次,但是相对⽽⾔,插⼊相同数量的结点,红⿊树的旋转次数是更少的,因为他对平衡的控制没那么严格。
2. 红黑树的实现
2.1 红黑树的结构
2.2红黑树的插入
2.2.1红黑树插入,旋转的一些细节
前提!!!插⼊⼀个值按⼆叉搜索树规则进⾏插⼊,插⼊后我们只需要观察是否符合红⿊树的4条规则。
1. 插⼊⼀个值按⼆叉搜索树规则进⾏插⼊,插⼊后我们只需要观察是否符合红⿊树的4条规则。
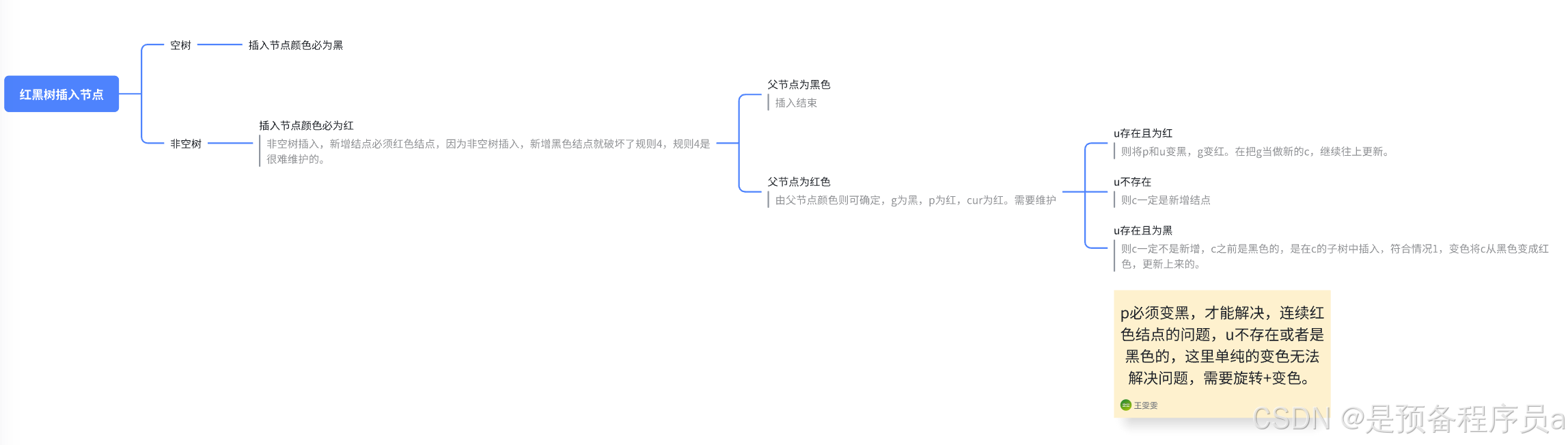
2. 如果是空树插⼊,新增结点是⿊⾊结点。如果是⾮空树插⼊,新增结点必须红⾊结点,因为⾮空树插⼊,新增⿊⾊结点就破坏了规则4,规则4是很难维护的。
3. ⾮空树插⼊后,新增结点必须红⾊结点,如果⽗亲结点是⿊⾊的,则没有违反任何规则,插⼊结束。
4. ⾮空树插⼊后,新增结点必须红⾊结点,如果⽗亲结点是红⾊的,则违反规则3。进⼀步分析,c是红⾊,p为红,g必为⿊,这三个颜⾊都固定了,关键的变化看u的情况,需要根据u分为以下⼏种情况分别处理。
2.2.1.1 u(uncle)不存在 ,c为p的左孩子(单旋+变色)
2.2.1.2 uncle存在且为黑,c为p的左孩子(单旋+变色)
2.2.1.3 u(uncle)不存在 ,c为p的右孩子(双旋+变色)
2.2.1.4 uncle存在且为黑,c为p的右孩子(双旋+变色)
2.3插入节点的代码实现

3. 本期关于红黑树的总结:
我觉得有一些难度,特别是在选旋转这里,要不是我为了写博客,在上完课之后,又梳理了一边。整体将清楚的结构写了下来,希望对大家有真的帮助。