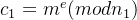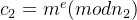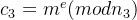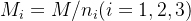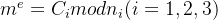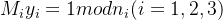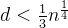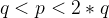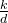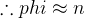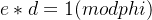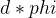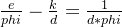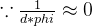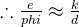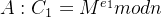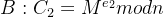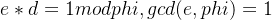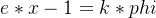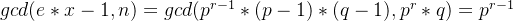RSA加密与解密
(1)e和phi不互素,但是e和p−1或者q−1互素,转化到模p或者模q下求解
(2)_gcd=gcd(e,phi)=2比较小,直接iroot开e//_gcd次根
(3)gcd(e,phi)=16也比较小,但尝试iroot开根跑不出来,这时考虑有限域内开方来求解
(4)gcd(e,φ(n))=e=1009算是很大了,且gcd(e,p−1) = e = 1009.直接用AMM
简介
在计算机中常用的加密算法分为两类:对称加密算法和非对称加密算法。
1.对称加密
在对称加密技术中,对信息的加密和解密都使用了相同的密钥Key,也就是说使用同一个密钥Key对数据进行加密和解密。这种加密方法可简化加解密的处理过程,信息交换双方都不必彼此研究和交换专用的加解密算法。如果在交换阶段,密钥Key没有泄露,那么加密数据的机密性和报文的完整性就可以得到保证。
2.非对称加密
在非对称加密中,不再只有一个密钥Key了。在非对称加密算法中,密钥被分解为一对,一个称为公开密钥,另一个称为私有密钥。对于公钥,可以通过非保密方式向他人公开,而私钥则由解密方保密,不对别人公开。
最具有代表性的非对称加密方式就是RSA公钥密码体制。
RSA算法的基础操作步骤
1.生成公钥和私钥
生成公钥PK和私钥SK的步骤如下:
(1)随意选择两个大的素数P、Q,P不等于Q。
(2)将P、Q两个素数相乘得到一个N,即N=P*Q
(3)将P、Q分别减一,再相乘,得到一个数T,即T=(Q-1)*(P-1)
(4)选择一个整数E,作为一个密钥,使E与T互质(即E与T的最大公约数为1),且E必须小于T。
(5)根据公式D*E mod T = 1 ,计算出D的值,作为另一个密钥。
(6)通过以上的步骤就可以求出N,E,D这三个数据,其中(N,E)作为公钥,(N,D)作为私钥。
2.用公钥加密信息
发送信息的一方收到公钥PK后,就可以通过公钥PK对数据进行加密,加密的操作步骤如下图所示,其中明文为:M,密文为:C
明文:M
加密:
密文 :C
3.用私钥解密信息
接收方持有私钥(N,D)在接受到密文C后,既可以通过私钥解密,得到明文M,解密过程如下:
密文:C
解密:
明文:M
攻击类型
(一)低加密指数攻击
(1)e=3时的小明文攻击:
特点:e=3,m很小,n很大
1.当 e=3 时,如果明文过小,导致明文的三次方仍然小于n,那么通过直接对密文开三次方即可得到明文。
即: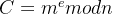
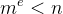
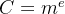
2.如果明文的三次方比n大,但不是足够大,那么设k有:
爆破k,如果C−k∗n或者C+k∗n能开三次根式,那么就可以直接得到明文。
关键代码:
from libnum import* #python第三方库
from gmpy2 import* #python第三方库
n= ......
c= ......
i=0
while 1:
if(iroot(c+i*n,3)[1]==1): #或者 iroot(c-i*n,3)
print(iroot(c+i*n,3)[0])
break
i=i+1
(2)e=2时的小明文攻击:
e=2时,直接将密文C开平方获得解
由于e只有2,相当于把明文m平方而已,得到的C也比n小很多。尝试直接将C开根号看能否得到明文。
from libnum import* #python第三方库
from gmpy2 import* #python第三方库
c=...... #C的值
m=isqrt(c) #开平方根
#m=iroot(c,2)[0] #开C的二次方根
print(n2s(m)) #字符串转数字
(3)e=1时的小明文攻击:
加密过程:C≡m mod n ,明文与密文同模
所以有:m=C+n*k,爆破k
from libnum import*
n=....
c=....
max_num = 7 #设置遍历上限
for k in range(max_num):
m = c + n*k
print(n2s(m))
(二)低加密指数广播攻击
如果选取的加密指数较低,并且使用相同的加密指数给一个接受者的群发送相同的信息,那么可以进行广播攻击得到明文
特点:n非常大,e一般很小。
(1)基础题型:
加密指数e非常小。一般拿到的是多组n和c,且只有一个e,e还很小,且模数n不同,但使用相同的加密指数e进行多次加密。
import gmpy2
import os
from functools import reduce
from Crypto.Util.number import long_to_bytes
def CRT(items):
N = reduce(lambda x, y: x * y, (i[1] for i in items))
result = 0
for a, n in items:
m = N // n
d, r, s = gmpy2.gcdext(n, m)
if d != 1:
raise Exception("Input not pairwise co-prime")
result += a * s * m
return result % N, N
# e, n, c
e =
n=[]
c=[]
data = list(zip(c, n)) # zip()将对象打包成元组
x, n = CRT(data)
m = gmpy2.iroot(gmpy2.mpz(x), e)[0].digits()
print('m is: ' + long_to_bytes(m))
(2)进阶之爆破e:
题目中不直接给出e。一份明文使用不同的模数n,相同的加密指数e进行多次加密,可以拿到每一份加密后的密文和对应的模数n、加密指数e。
对上述等式运用中国剩余定理求解出m的e次方,然后爆破e即可求出明文。
中国剩余定理:设n1,n2,n3是两两互素的正整数,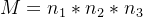
则同余式组:
有唯一解:
其中
import gmpy2
import os
from functools import reduce
from Crypto.Util.number import long_to_bytes
def CRT(items):
N = reduce(lambda x, y: x * y, (i[1] for i in items)) # n_i 的乘积,N=n1*n2*n3
result = 0
for a, n in items:
m = N // n #M_i=M/n_i
d, r, s = gmpy2.gcdext(n, m)
if d != 1:
raise Exception("Input not pairwise co-prime")
result += a * s * m
return result % N, N
# e, n, c
e = 1
n=[n1,n2,n3……]
c=[c1,c2,c3……]
data = list(zip(c, n))
x, n = CRT(data)
for i in range(1,30):
e = i
m = gmpy2.iroot(gmpy2.mpz(x), e)[0].digits()
print('m is: ' + long_to_bytes(m))
(3)进阶之公因数求解:
某些题目会给出多组n和c,但是e却不小,比如e=65537,这种情况下不建议使用中国剩余定理求解,可以尝试在n中寻找最大公约数gcd。
由于模数n只能分解为p和q,所以当n很多时,p或q有相同的风险,因此不同的模数n中可能存在相同的p或者q。求出不同n之间的最大公约数 gcd()从而得到p或q,进而可得d,有私钥d就能得到明文。
import gmpy2
import libnum
e = 65537
n0 =
c0 =
n1 =
c1 =
n2 =
c2 =
n3 =
c3 =
n4 =
c4 =
n5 =
c5 =
n6 =
c6 =
n7 =
c7 =
n8 =
c8 =
n9 =
c9 =
n10 =
c10 =
n=[n0,n1,n2,n3,n4,n5,n6,n7,n8,n9,n10……]
c=[c0,c1,c2,c3,c4,c5,c6,c7,c8,c9,c10……]
for i in range(len(n)):
for j in range(len(n)):
if(i!=j):
if(gmpy2.gcd(n[i],n[j])!=1): #对不同的n进行 欧几里得算法,以求出最大公约数(p)
print(i,j) #输出对应的n的序号
p = gmpy2.gcd(n[i],n[j])
print("p = ",p)
q = n[i] // p
print("q = ",q)
d = gmpy2.invert(e , (p-1)*(q-1))
print("d = ",d)
m = pow(c[i],d,n[i])
print("m = ",m)
print(libnum.n2s(int(m)))
(三)低解密指数攻击(Wiener Attack)
与低加密指数相同,低解密指数可以加快解密的过程,但同时也带来了安全问题。Wiener表示如果满足:
那么一种基于连分数(数论中的问题)的特殊攻击类型,就可以危害RSA的安全,此时需要满足:
如果满足上述条件,通过Wiener Attack 可以在多项式时间中分解n。
攻击原理:理论基础(勒让德定理):当e过大或过小时,
由(4)两边同时除
可得:
虽然在此式子中无法得知d和k的具体值,但是由于连分数逼近原理可以得到两者之间的比值,所以(p+q)是可以得到相对接近的值的
再通过构造方程
韦达定理:
求解方程即可得到p,q的值
特点:e过大或过小,且n分解无望
下载工具:rsa-wiener-attack
github上有公开的攻击代码。
将解密的代码放入wiener-attack的目录下即可。
使用:wiener攻击脚本用于求出d的值(注意,这里要将攻击脚本和rsa-wiener-attack的py文件放在同一个目录下)
import RSAwienerHacker
n =
e =
d = RSAwienerHacker.hack_RSA(e,n)
if d:
print(d)
代码实现:
(SageMath)
c = continued_fraction(e/n) #直接输出e/n的连分数展开的数组
alist = c.convergents() #求e/n的连分数逼近
(Python)
from Crypto.Util.number import long_to_bytes
from gmpy2 import invert,isqrt
from libnum import n2s,s2n
#低解密指数攻击
#条件:d<pow(n,0.25)/3
def RSA_wiener (n,e,c):
#连分数逼近,并列出逼近过程中的分子与分母
def lian_fen(x,y):
res = []
while y:
res.append(x//y)
x,y = y,x%y
resu = []
for j in range(len(res)):
a,b = 1,0
for i in res[j::-1]:
b,a = a,a*i+b
resu.append((a,b))
if resu[0] == (0,1):
resu.remove((0,1))
return resu[:-1]
lianfen = lian_fen(e,n)
def get_pq(a,b,c):
par = isqrt((n-phi+1)**2-4*n)
x1,x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
return x1,x2
for (k,d) in lianfen:
phi = (e*d-1)//k
p,q = get_pq(1,n-phi+1,n)
if p*q == n:
p,q = abs(int(p)),abs(int(q))
d = invert(e,(p-1)*(q-1))
break
return m,long_to_bytes(pow(c,d,n))
(四)共模攻击
共模攻击,Common Modulus Attack,也称为同模攻击。同模攻击利用的大前提就是,RSA体系在生成密钥的过程中使用了相同的模数n。
对于同一条明文m, A和B对其进行加密:
如果,此时有一个攻击者,同时监听了A和B接收到的密文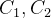
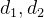
from libnum import* #python第三方库
from gmpy2 import* #python第三方库
n =
c1 =
c2 =
e1 =
e2 =
s = gcdext(e1,e2) #gmpy2.gcdext(),扩展欧几里得算法,返回tuple元组,满足s[1]*e1+s[2]*e2=1
m = pow(c1,s[1],n)*pow(c2,s[2],n)%n #获取明文m
print(n2s(m))
(五)模不互素
存在多个模数,且 gcd(n1,n2)!=1
import gmpy2
import libnum
def gcd(a, b):
if a < b:
a, b = b, a
while b != 0:
temp = a % b
a = b
b = temp
print a
return a
def n2s(num):
t = hex(num)[2:]
if len(t) % 2 == 1:
t = '0' + t
return ''.join([chr(int(b, 16)) for b in [t[i:i + 2] for i in range(0, len(t), 2)]])
n1=
n2=
e=
c1=
c2=
q=gcd(n1,n2)
p1=n1//q
p2=n2//q
phi=(p1-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c1,d,n1)
print(n2s(m))
(六)e与phi不互素
gcd(e,phi)比较小时可以考虑iroot直接开根,当直接开根跑不出来时,考虑有限域内开方
gcd(e,phi)很大时,考虑AMM算法
(1)e和phi不互素,但是e和p−1或者q−1互素,转化到模p或者模q下求解
from Crypto.Util.number import *
p=
q=
e=
c =
n = p*q
# _gcd = gcd(e,(p-1)*(q-1)) # 65537
gcd_q = gcd(e,q-1) # 1
d = inverse(e,q-1)
m = pow(c,d,q)
print(long_to_bytes(int(m)))
因为gcd(e,phi)=e=65537很大,可以用AMM算法求解
(SageMath)
import random
import math
import time
from Crypto.Util.number import bytes_to_long,long_to_bytes
p = 0
#设置模数
def GF(a):
global p
p = a
#乘法取模
def g(a,b):
global p
return pow(a,b,p)
def AMM(x,e,p):
GF(p)
y = random.randint(1, p-1)
while g(y, (p-1)//e) == 1:
y = random.randint(1, p-1)
print(y)
print("find")
#p-1 = e^t*s
t = 1
s = 0
while p % e == 0:
t += 1
print(t)
s = p // (e**t)
print('e =',e)
print('p =',p)
print('s =',s)
print('t =',t)
# s|ralpha-1
k = 1
while((s * k + 1) % e != 0):
k += 1
alpha = (s * k + 1) // e
#计算a = y^s b = x^s h =1
#h为e次非剩余部分的积
a = g(y, (e ** (t - 1) ) * s)
b = g(x, e * alpha - 1)
c = g(y, s)
h = 1
for i in range(1, t-1):
d = g(b,e**(t-1-i))
if d == 1:
j = 0
else:
j = -math.log(d,a)
b = b * (g(g(c, e), j))
h = h * g(c, j)
c = g(c, e)
#return (g(x, alpha * h)) % p
root = (g(x, alpha * h)) % p
roots = set()
for i in range(e):
mp2 = root * g(a,i) %p
assert(g(mp2, e) == x)
roots.add(mp2)
return roots
# def check(m):
# if 'flag' in m:
# print(m)
# return True
# else:
# return False
p=
q=
e=
c =
n = p*q
mps = AMM(c,e,p)
for mpp in mps:
solution = long_to_bytes(int(mpp))
if b'flag' in solution:
#solution = int(mpp)
print(solution)
(2)_gcd=gcd(e,phi)=2比较小,直接iroot开e//_gcd次根
import gmpy2
import libnum
p =
q =
e =
c =
n = p*q
phi = (p-1)*(q-1)
_gcd = gmpy2.gcd(e, phi)
d = gmpy2.invert(e//_gcd, phi)
m_gcd = gmpy2.powmod(c, d, n)
m = gmpy2.iroot(m_gcd1, _gcd)
flag = libnum.n2s(int(m[0]))
print(flag)
(3)gcd(e,phi)=16也比较小,但尝试iroot开根跑不出来,这时考虑有限域内开方来求解
(SageMath)
from Crypto.Util.number import *
p =
q =
c =
e =
n = p*q
P.<a>=PolynomialRing(Zmod(p),implementation='NTL')
f=a^e-c
mps=f.monic().roots()
P.<a>=PolynomialRing(Zmod(q),implementation='NTL')
g=a^e-c
mqs=g.monic().roots()
#定义了一个名为P的多项式环,a是这个环里面的变量,Zmod(p)是在模p下定义了一个整数环。多项式的每一个#系数都是p的倍数,这样才能确保在模p下进行运算时不会出现浮点数。
#参数implementation='NTL'指示SageMath使用NTL(Number Theory Library)作为该环的实现。
#f=a^e-c定义了一个多项式,monic()是将多项式首一化
#f.roots()得到方程的一个根的列表,该列表包含f(x)=a^e-c在模p意义下的所有根。
#列表中的每个元素的格式为 (a,1),在此二元组表示中,1表示多重根,即该解在方程中的出现次数。
flag=[]
for mpp in mps:
x=mpp[0]
for mqq in mqs:
y=mqq[0]
solution = CRT_list([int(x), int(y)], [p, q])
flag.append(solution)
for i in flag:
m=long_to_bytes(i)
if b'flag'in m:
print(m)
(4)gcd(e,φ(n))=e=1009算是很大了,且gcd(e,p−1) = e = 1009.直接用AMM
(SageMath)
from Crypto.Util.number import *
import random
import math
def onemod(e, q):
p = random.randint(1, q-1)
while(powmod(p, (q-1)//e, q) == 1): # (r,s)=1
p = random.randint(1, q)
return p
def AMM_rth(o, r, q): # r|(q-1)
"""
x^r % q = o
:param o:
:param r:
:param q:
:return:
"""
assert((q-1) % r == 0)
p = onemod(r, q)
t = 0
s = q-1
while(s % r == 0):
s = s//r
t += 1
k = 1
while((s*k+1) % r != 0):
k += 1
alp = (s*k+1)//r
a = powmod(p, r**(t-1)*s, q)
b = powmod(o, r*a-1, q)
c = powmod(p, s, q)
h = 1
for i in range(1, t-1):
d = powmod(int(b), r**(t-1-i), q)
if d == 1:
j = 0
else:
j = (-int(math.log(d, a))) % r
b = (b*(c**(r*j))) % q
h = (h*c**j) % q
c = (c*r) % q
result = (powmod(o, alp, q)*h)
return result
def ALL_Solution(m, q, rt, cq, e):
mp = []
for pr in rt:
r = (pr*m) % q
# assert(pow(r, e, q) == cq)
mp.append(r)
return mp
def ALL_ROOT2(r, q): # use function set() and .add() ensure that the generated elements are not repeated
li = set()
while(len(li) < r):
p = powmod(random.randint(1, q-1), (q-1)//r, q)
li.add(p)
return li
def attack(p, q, e, check=None):
cp = c % p
cq = c % q
mp = AMM_rth(cp, e, p)
mq = AMM_rth(cq, e, q)
rt1 = ALL_ROOT2(e, p)
rt2 = ALL_ROOT2(e, q)
amp = ALL_Solution(mp, p, rt1, cp, e)
amq = ALL_Solution(mq, q, rt2, cq, e)
if check is not None:
j = 1
t1 = invert(q, p)
t2 = invert(p, q)
for mp1 in amp:
for mq1 in amq:
j += 1
if j % 1000000 == 0:
print(j)
ans = (mp1 * t1 * q + mq1 * t2 * p) % (p * q)
if check(ans):
return ans
return amp, amq
def calc(mp, mq, e, p, q):
i = 1
j = 1
t1 = invert(q, p)
t2 = invert(p, q)
for mp1 in mp:
for mq1 in mq:
j += 1
if j % 1000000 == 0:
print(j)
ans = (mp1*t1*q+mq1*t2*p) % (p*q)
if check(ans):
return
return
def check(m):
try:
a = long_to_bytes(m)
if b'NSSCTF' in a:
print(a)
return True
else:
return False
except:
return False
if __name__ == '__main__':
e = 1009
n =
c =
p =
q =
cp = c % p
cq = c % q
mp = AMM_rth(cp, e, p)
mq = AMM_rth(cq, e, q)
rt1 = ALL_ROOT2(e, p)
rt2 = ALL_ROOT2(e, q)
amp = ALL_Solution(mp, p, rt1, cp, e)
amq = ALL_Solution(mq, q, rt2, cq, e)
calc(amp, amq, e, p, q)
(5)n=p^r*q 时,e和phi不互素问题
先恢复p、q
在多项式时间内求解上面方程(copper)求出d.
因为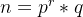
用 small_roots() 开r-1次方就能恢复 p
(SageMath)
from gmpy2 import *
hint =
n =
e =
c =
P.<d> = PolynomialRing(Zmod(n))
f = e*d - 251
res = f.monic().small_roots(X = 2^256,beta = 0.4)
p_4 = gcd(int(f(res[0])),n)
p = iroot(p_4,4)[0]
q = n//p**4
print(f"p,q = {p},{q}")
接下来就是有限域开方的问题了
(SageMath)
# 开251次方
from Crypto.Util.number import *
import itertools
hint =
n =
e =
c =
p,q= ,
p_list = [p,q]
n_list = [p**5,q]
print(n_list)
res=[]
for pi in n_list:
d = inverse(int(e//251),euler_phi(pi)) # 对n_listt 每一个 pi 求欧拉函数
m = pow(c,d,pi)
temp = (Zmod(pi)(m).nth_root(251, all=True))
#print('temp =',temp) # 列表 251
if temp is not None:
res.append(temp)
else:
print("None")
for vc in itertools.product(*res):
_c = [int(x) for x in vc]
m = long_to_bytes(int(crt(_c, n_list)))
if b"flag" in m:
print(m)
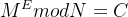
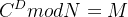
![m=\sqrt[3]{C}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9tJTNEJTVDc3FydCU1QjMlNUQlN0JDJTdE)