#又来按时更新帖子啦,现在学习一个更复杂(也就复杂一丢丢)的模型啦,多项式回归,还是一样,带大家了解多项式回归,如何建立模型,如何运用模型,如何使用这个模型来拟合自己的数据集,如何做出预测。代码解析超级详细,适合建模新手学习#
多项式回归
建议新手宝子先看一下前面的帖子,了解一下再来学习新的模型。
在统计学和机器学习中,多项式回归是一种线性回归的扩展形式,它使用多项式函数来拟合数据。多项式回归通过增加输入特征的幂次项来捕捉数据中的非线性关系。在最简单的情况下,一次多项式回归就是简单的线性回归模型,而更高阶的多项式回归则可以更好地模拟更复杂的曲线形状。
简单来说就是线性回归的升级版,函数中加入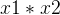
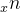
项目分析
项目介绍:
随机生成四十个二维数据作为X值,求出每个数的sin值作为y值,加入适当噪声,模拟现实数据 使用多项式回归模型拟合加入噪声的sin函数 生成新的数据,并由训练的模型求出预测的y值,绘制出新的坐标图,对比散点图观察拟合效果
逐项解析
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
import numpy as np
import matplotlib.pyplot as pltPolynomialFeatures 用于生成多项式特征(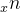
# 生成一些非线性数据
np.random.seed(0) # 指定随机数生成器种子,指定后可以每次运行的时候产生的随机数相同,将零修改为一,将会改变生成数的值,但是每次运行的时候产生的数字还是和第一次相同
X = np.sort(5 * np.random.rand(40, 1), axis=0) # 随机生成(0,5)的40*1的二维数组,40个样本,1个特征首先创建自己的数据集,这里np.random.seed(0)作用是生成随机数种子,这句代码的作用是让random函数每次生成的数据都是一样的,这样对于后期重现数据很方便,不管运行多少次,random产生的随机数都是一样的,没有这句代码的话,每次运行产生的随机数字就是不相同的。里面的数字0,可以修改为其他数字,每个数字都对应着一组不同的随机数,但是每次运行也都是一样的结果。
rand(40,1)这里会生成40组随机数据,每组数据只有一个特征,数据范围是(0,1),前面乘以5之后就是(0,5)之间的随机数了,sort内置函数就是排序功能,默认是升序。
这里介绍一下axis=0这个参数的用法,首先他的作用是对数据进行垂直操作或者水品操作,这是对应着sort,就是水平排序或者竖直排序,当时我也有点不理解,什么是水平操作,什么是数值操作,下面就用具体实例进行教学。
import numpy as np
a = np.array([[1,2,3],
[8,5,1],
[9,1,2]])
a_sort = np.sort(a,axis = 0)这里数据是3 * 3,三个样本三个特征的一组数据,观察axis的用法,axis = 0,数组沿着竖直方向进行操作,这里是进行排序操作,默认升序,第一列数据1 8 9,结果不改变,第二列 2 5 1,结果变为 1 2 5,竖直方向进行了升序操作,第三列同理,axis = 1,数据就沿着水平方向操作,原理同上,大家可以自己操作一下,后续自己的数据也可以这样进行处理。
进行这样操作之后,40*1的数组就变成递增的数组了,便于后续数据拟合。
y = np.sin(X).ravel() # 基础信号,求出sin值,并且ravel将函数平铺成一维
'''
y=[[1,2,3],[4,5,6],[7,8,9]]
经过.ravel处理后变为[1 2 3 4 5 6 7 8 9]
'''
y[::5] += 3 * (0.5 - np.random.rand(8)) # 添加一些噪声
'''
加入噪声处理,对于展开后的y,每隔五个加一个随机噪声,噪声为[-1.5,1.5]之间的数
rand(1)表示每个y加上的随机数字相同,8表示一个需要加入八个随机数,各不相同,不能填写其他的数字
'''ravel 函数对数据进行将维操作,图上实例,将二维展开编程一维数组,首先对每个x值求正弦,此次目的就是使用多项式回归拟合加入噪声的正弦函数。
y[::5]对数组进行切片操作,每隔5个数据加入噪声,本来是连续的sin函数图像,现在隔上5个点加入随机数,使得图像不连续,模拟现实生活中的离群点。我尝试了一下这里的rand()里面只能填8或者1,1表示加入的所有噪声数值相同,8表示加入的所有噪声值不同,一共有四十个数据,五个进行切片,所以最后需要八个数据,大家可以根据实际情况而定,数值操作代码会报错。
# 使用多项式特征转换器和线性回归
degree = 3 # 选择多项式的阶数
model = make_pipeline(PolynomialFeatures(degree), LinearRegression()) # 结合多项式特征和线性回归模型,可以构造出一个非线性模型degree设置多项式的阶数,这里表示使用三阶多项式进行拟合,阶数表示多项式中未知数的最高次数,这里跟泰勒公式有点像,泰勒公式的基本思想是利用函数在某一点及其各阶导数值的信息来构造一个多项式,使得这个多项式与原函数在这一点上尽可能接近,并且随着多项式的阶数增加,逼近的效果会越来越好。但是这里多项式回归,设置阶数越多效果不一定越好,阶数越高,多项式捕捉到的特征就越多,有可能就将现实数据的噪声学习进去,导致模型过拟合。
这里函数的用法make_pipeline创建一个管道,对线性回归和多项式进行融合,建立一个非线性模型。
model.fit(X, y) # 向预先设置好的模型中填入数据进行训练
# 预测新数据
X_new = np.linspace(0, 5, 100)[:, np.newaxis] # 生成一系列数据点,用来绘制回归模型的预测曲线这里使用fit函数将预先设置好的数据传入进去,model里面会自动生成一个多项式与当前数据进行拟合,最后使用刚刚建立好的模型进行数据预测。
X_new生成(0,5)之间一百个数据,np.linspace 用于生成0-5之间的等差数列,np.newaxis用于增加维度,[:,np.newaxis]将生成的一维数组变为二维数组,为了与原始数据格式相同。如数组[1,2,3],增加维度后变为[[1],[2],[3]]。
# 得到生成的数据的预测结果
y_new = model.predict(X_new)
# 绘制结果
plt.scatter(X, y, color='black')
# 函数用于创建散点图,用来显示原始数据点
plt.plot(X_new, y_new, color='blue', linewidth=3)
plt.title(f"Degree {degree} Polynomial Regression") # 三次多项式回归
plt.xlabel("Feature")
plt.ylabel("predict")
plt.show()使用predict函数预测每个X_new对应的y值,调用plot函数进行绘制图像。
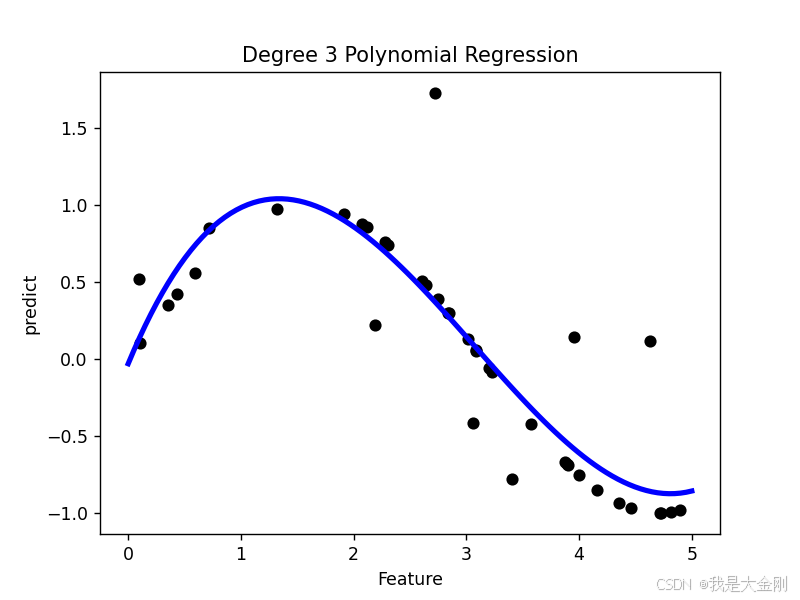
最后结果如下:
散点图就是加入了噪声的原始正弦函数图像,蓝色曲线是使用三阶多项式进行数据拟合得到的函数图像,最后拟合效果还是挺好的,大部分点都落在图像上。
完整代码如下,大家可以使用自己的数据集进行尝试哦,使用pandas库调用本地的csv文件,导入表格数据,使用模型进行数据拟合,对自己数据进行预测:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
import numpy as np
import matplotlib.pyplot as plt
'''
随机生成四十个二维数据作为X值,求出每个数的sin值作为y值,加入适当噪声,模拟现实数据
使用多项式回归模型拟合sin函数图像,生成原始数据的散点图
生成新的数据,并由训练的模型求出预测的y值,绘制出新的坐标图,对比散点图观察拟合效果
求出每个数的sin值加上噪声代替了现实中的真实数据
'''
# 生成一些非线性数据
np.random.seed(0) # 指定随机数生成器种子,指定后可以每次运行的时候产生的随机数相同,将零修改为一,将会改变生成数的值,但是每次运行的时候产生的数字还是和第一次相同
X = np.sort(5 * np.random.rand(40, 1), axis=0) # 随机生成(0,5)的40*1的二维数组,40个样本,1个特征
'''
a = np.array([[1,3],[4,2],[0,9]])
b=np.sort(a,axis=0)
axis = 0,数组沿着竖直方向操作,在当前排序情况下,数组运行结果为:
[
[0,2]
[1,3]
[4,9]
]
'''
y = np.sin(X).ravel() # 基础信号,求出sin值,并且ravel将函数平铺成一维
'''
y=[[1,2,3],[4,5,6],[7,8,9]]
经过.ravel处理后变为[1 2 3 4 5 6 7 8 9]
'''
y[::5] += 3 * (0.5 - np.random.rand(8)) # 添加一些噪声
'''
加入噪声处理,对于展开后的y,每隔五个加一个随机噪声,噪声为[-1.5,1.5]之间的数
rand(1)表示每个y加上的随机数字相同,8表示一个需要加入八个随机数,各不相同,不能填写其他的数字
'''
# 使用多项式特征转换器和线性回归
degree = 3 # 选择多项式的阶数
model = make_pipeline(PolynomialFeatures(degree), LinearRegression()) # 结合多项式特征和线性回归模型,可以构造出一个非线性模型
'''
多项式特征表示在原始特征的基础上构造出更高次数幂的特征
单一特征(只包含一个x),构造多项式特征可以包括x**2,x**3,对于多个特征的情况,可以添加不同特征之间的乘积(x1*x2)
特征的转化有助于捕捉数据之间的非线性关系
'''
# 拟合模型
model.fit(X, y) # 向预先设置好的模型中填入数据进行训练
# 预测新数据
X_new = np.linspace(0, 5, 100)[:, np.newaxis] # 生成一系列数据点,用来绘制回归模型的预测曲线
'''
转化为二维数组是为了与模型兼容
np.linspace用于生成(0,5)的等差数列共一百个
[:,np.newaxis]用于将生成的一维数组转化为二维数组
np.newaxis用于增加维度
如数组[1,2,3],增加维度后变为[[1],[2],[3]]
'''
# 得到生成的数据的预测结果
y_new = model.predict(X_new)
# 绘制结果
plt.scatter(X, y, color='black')
# 函数用于创建散点图,用来显示原始数据点
plt.plot(X_new, y_new, color='blue', linewidth=3)
plt.title(f"Degree {degree} Polynomial Regression") # 三次多项式回归
plt.xlabel("Feature")
plt.ylabel("predict")
plt.show()