1.题目解析

题目解析：647.回文子串——力扣

测试用例

2.算法原理  

1.状态表示

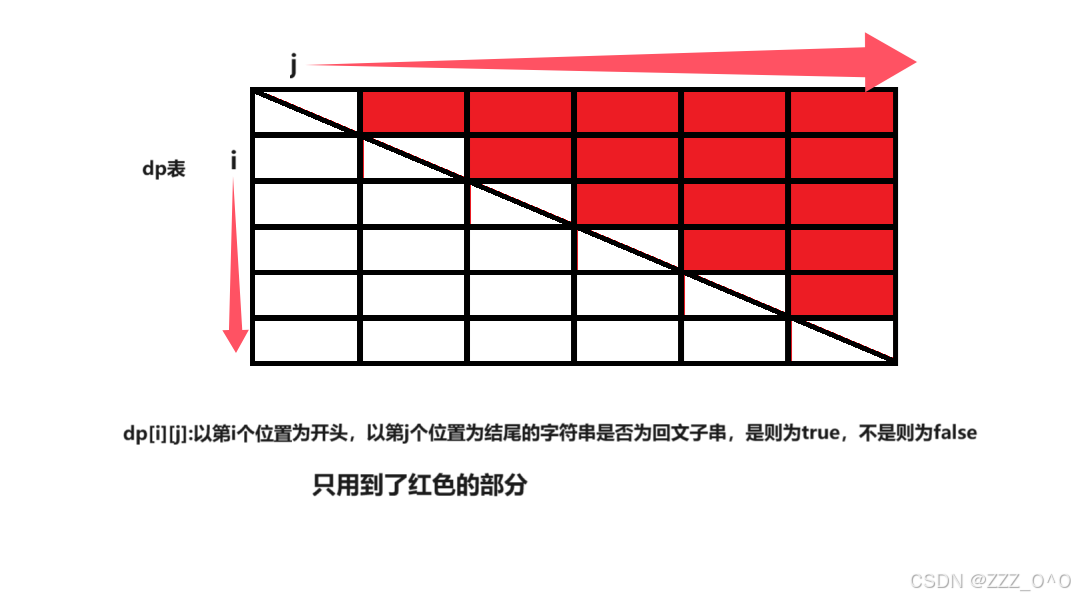
本题需要判断一段字符串是否为回文子串，因此最简单的方法就是保存起开始位置与结束位置，那么就需要一个二维的dp表来保存一段字符串是否为回文子串，dp表的数据类型为bool类型

dp[i][j]:以第i个位置开始，第j个位置结束的字符串是否为回文子串，是则为true，反之为false

2.状态转移方程

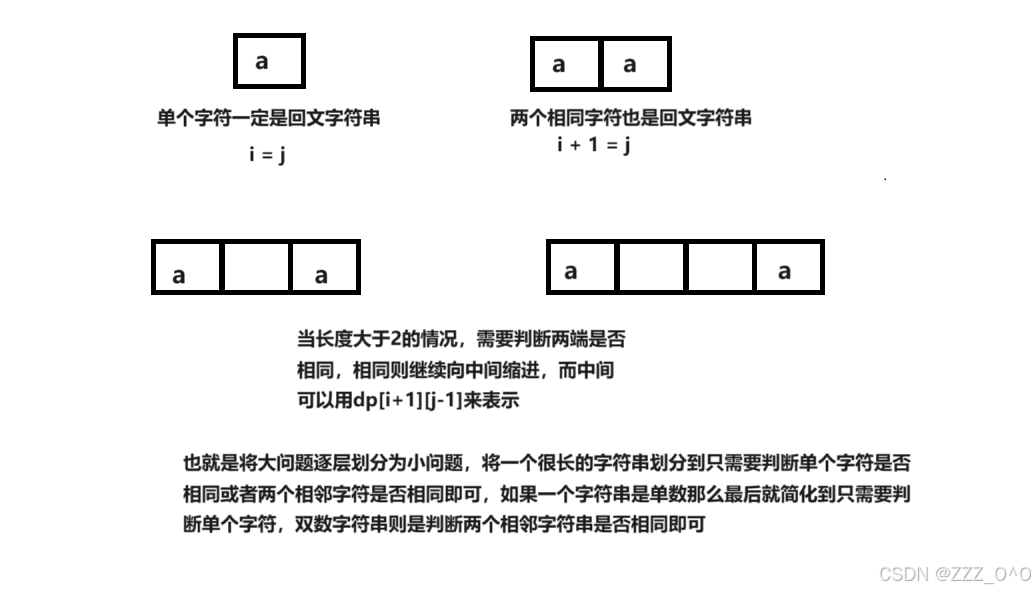
由于回文子串需要中心对称，因此判断完两端则需要向中间判断，也就是dp[i][j] = dp[i+1][j-1]，但是注意单个字符串与两个相同字符串的情况，这两种情况一定为回文子串，所以在判断前想确定此时的i+1<j是否成立，即一定保证要长度大于3，小于3就一定为true

状态转移方程为：if(s[i]==s[j])  dp[i][j] = i+1 < j ? dp[i+1][j-1] : true;

3.初始化

一开始就确定了单个字符与两个连续字符的情况，所以不用初始化

4.填表顺序

因为用到了i+1与j-1位置，根据状态表示的图示可以知道需要从下向上填表也就是i从后向前，j一定大于i小于n

5.返回值

返回dp表中true的个数

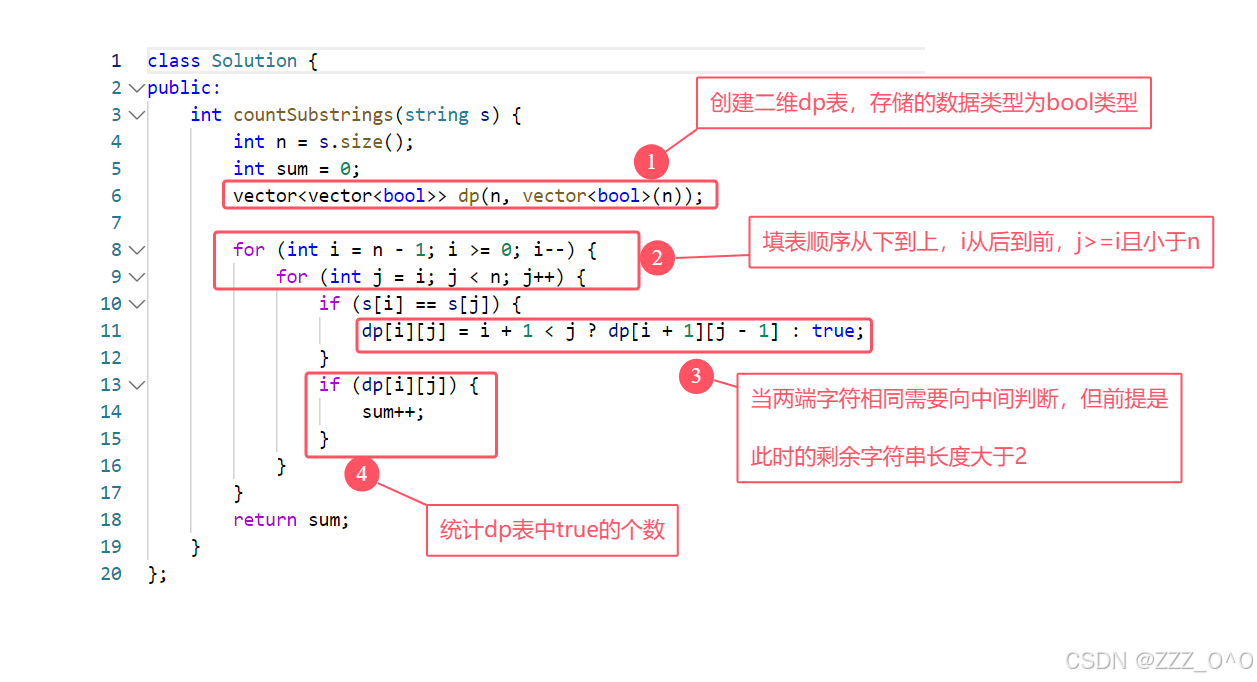
3.实战代码

代码解析 

class Solution {
public:
    int countSubstrings(string s) 
    {
        int n = s.size();
        int sum = 0;
        vector<vector<bool>> dp(n,vector<bool>(n));

        for(int i = n-1;i >= 0;i--)
        {
            for(int j = i;j < n;j++)
            {
                if(s[i] == s[j])
                {
                    dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true;
                }
                if(dp[i][j])
                {
                    sum++;
                }
            }
        }    
        return sum;
    }
};