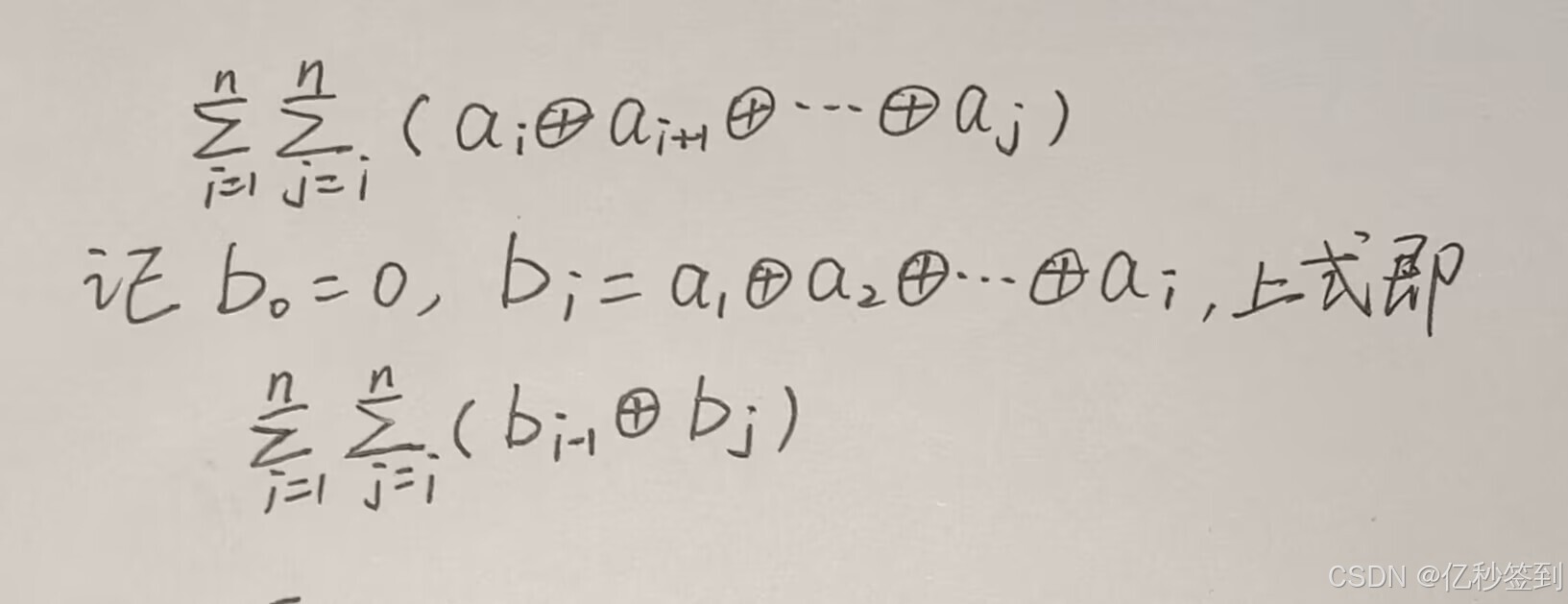1.异或和之和（14届蓝桥省A）

先用下异或前缀和：

 此时，对于给定i的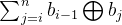，在知道[i，n]某位的1、0的个数后，即可算出。

区间[i,n]某位的1或0的个数可以用前缀和预处理，这样该部分的复杂度就为O(1)了，总复杂度也降为了O(n)。

#include<bits/stdc++.h>
using namespace std;
#define int long long 

signed main()
{
    int n; 
    cin>>n;
    vector<int>a(n+1),b=a;
    vector<vector<int>>fb(n+1,vector<int>(31));//fb[i][j]即b[1]~b[i]中第j位上为1的个数
    for(int i=1;i<=n;i++){
        cin>>a[i];
        b[i]=b[i-1]^a[i];//求a的异或前缀和
        fb[i]=fb[i-1];
        for(int j=0;j<=30;j++){
            if((b[i]>>j)&1)
            fb[i][j]++;
        }
    }

    int ans=0;
    for(int i=1;i<=n;i++){
        for(int j=0;j<=30;j++){
            int b1=fb[n][j]-fb[i-1][j];
            int b0=n-i+1-b1;
            if((b[i-1]>>j)&1)
            ans+=b0*(1<<j);
            else
            ans+=b1*(1<<j);
        }
    }
    cout<<ans<<endl;

}

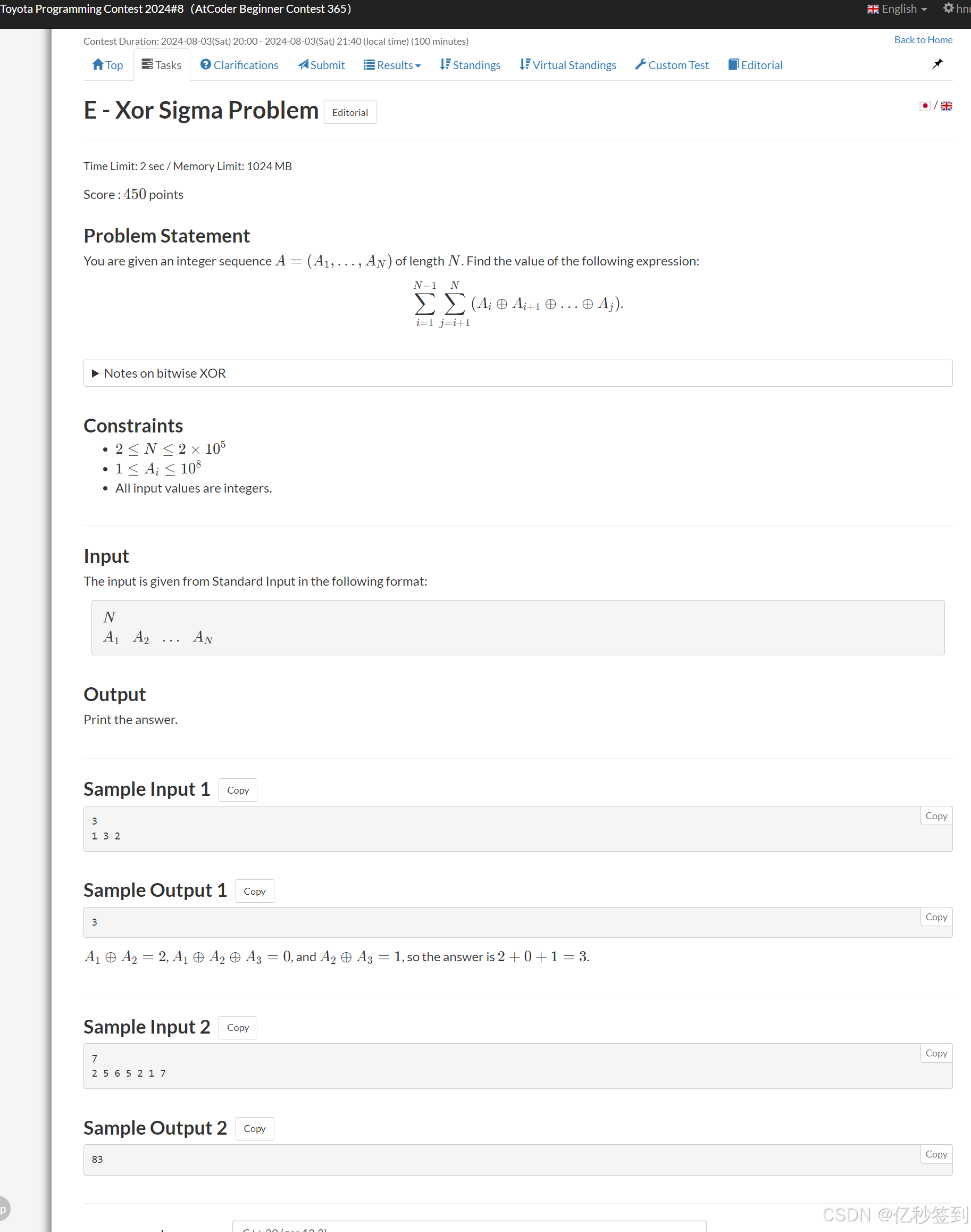
2. Xor Sigma Problem

同样的处理方式，代码也基本一样。注意一下标的区别就行了。

#include<bits/stdc++.h>
using namespace std;
#define int long long 

signed main()
{
    int n;
    cin>>n;
    vector<int>a(n+2),b=a;
    vector<vector<int> >fb(n+2,vector<int>(31));
    for(int i=1;i<=n;i++){
        cin>>a[i];
        b[i]=b[i-1]^a[i];
        f[i]=f[i-1];
        for(int j=0;j<=30;j++){
            if((b[i]>>j)&1)
            fb[i][j]++;
        }
    }

    int ans=0;
    for(int i=0;i<=n-2;i++){
        
        for(int j=0;j<=30;j++){
            int b1=fb[n][j]-fb[i+1][j];
            int b0=n-i-1;
            if((b[i]>>1)&1)
            ans+=b0*(1<<j);
            else
            ans+=b1*(1<<j);
        }
    }
    cout<<ans;

}

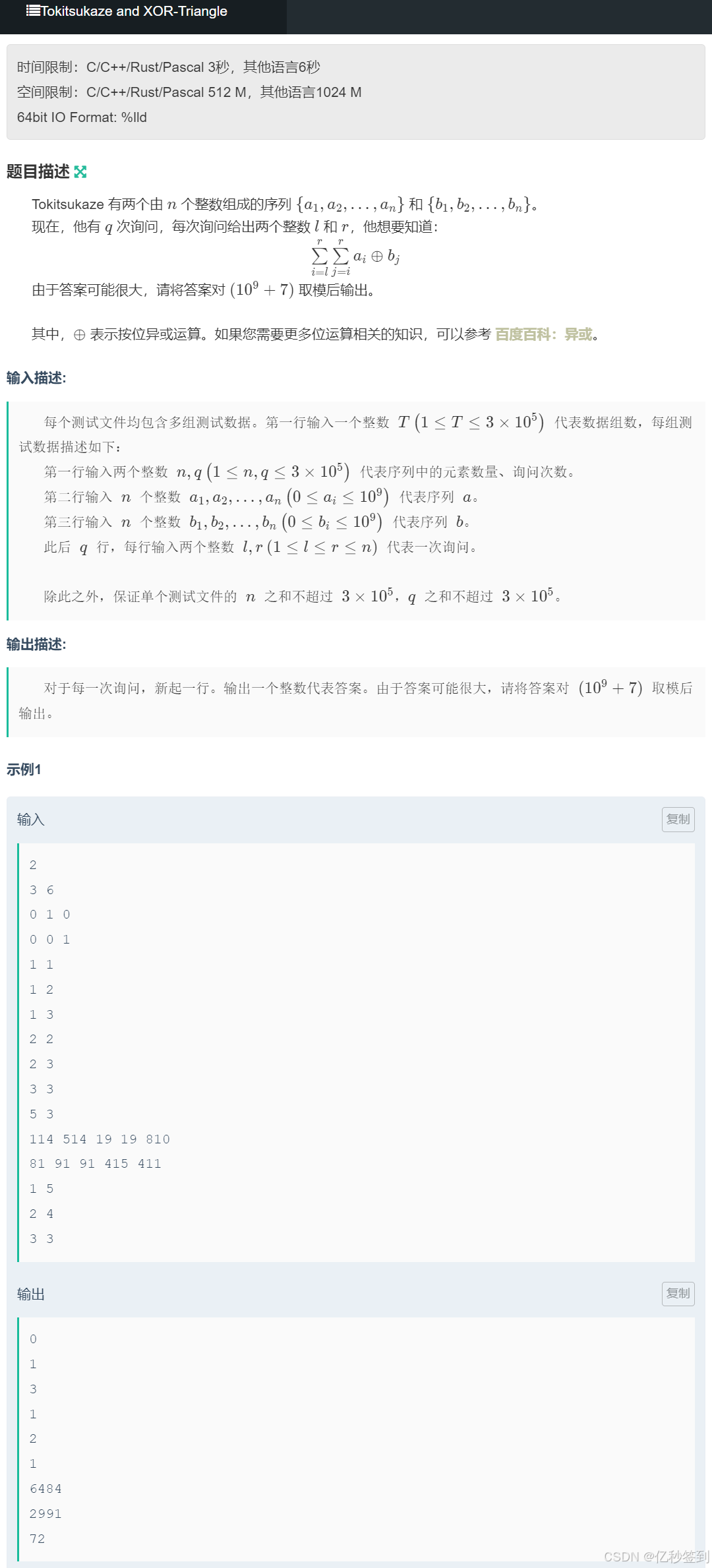
3.牛客寒假营4-L

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long 
#define ios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
const int M=1e9+7;

signed main()
{
    ios
    int T; 
    cin>>T;
    while(T--){
        int n,q; 
        cin>>n>>q;
        vector<int>a(n+1),b=a;
        vector fa(n+1,vector<int>(31)),fb=fa;
        vector<int>f(n+2);
        for(int i=1;i<=n;i++){
            cin>>a[i];
            fa[i]=fa[i-1];
            for(int j=0;j<=30;j++)
            if(a[i]&(1<<j)) 
            fa[i][j]++;
        }
        for(int i=1;i<=n;i++){
            cin>>b[i];
            fb[i]=fb[i-1];
            for(int j=0;j<=30;j++)
            if(b[i]&(1<<j))
            fb[i][j]++;
        }
        for(int i=n;i>=1;i--){
            f[i]=f[i+1];
            for(int j=0;j<=30;j++){
                int b1=fb[n][j]-fb[i-1][j];
                int b0=(n-i+1)-b1;
                if(a[i]&(1<<j))
                f[i]+=((int)1<<j)*b0%M;
                else
                f[i]+=((int)1<<j)*b1%M;
                f[i]%=M;
            }
        }
        while(q--){
            int l,r; 
            cin>>l>>r;
            auto ans=(f[l]-f[r+1]+M)%M;
            for(int i=0;i<=30;i++){
                int a1=fa[r][i]-fa[l-1][i];
                int b1=fb[n][i]-fb[r][i];
                int a0=(r-l+1)-a1;
                int b0=(n-r)-b1;
                auto t = (int)1*a1*b0+(int)1*a0*b1;
                ans-=(t%M)*(1<<i)%M;
                ans=(ans+M)%M;
            }
            cout<<ans<<endl;
        }
    }
    return 0;
}

 25/2/7