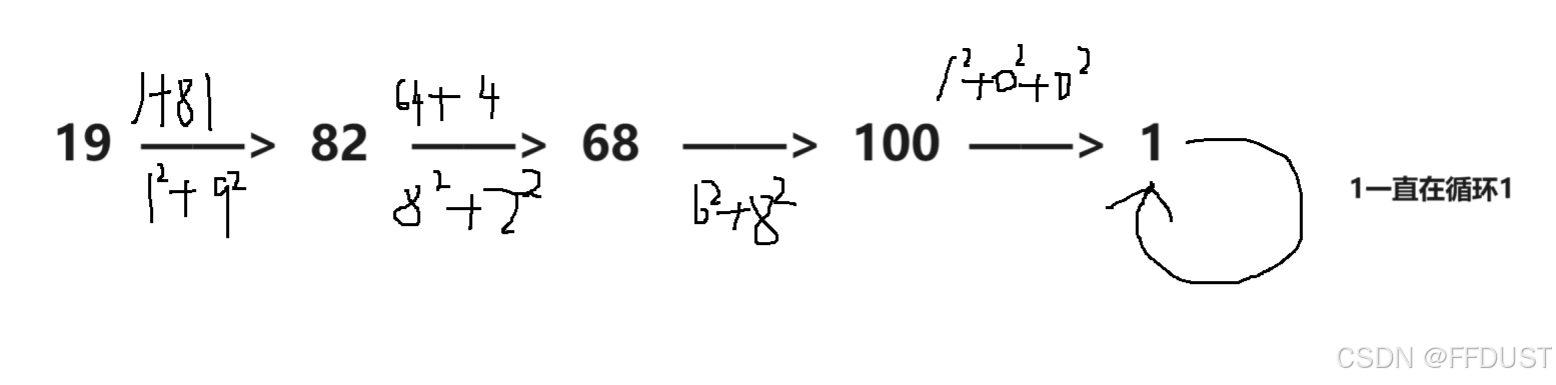目录

1. 题目解析 

2. 算法原理

3. 代码实现

 快乐数

1. 题目解析 

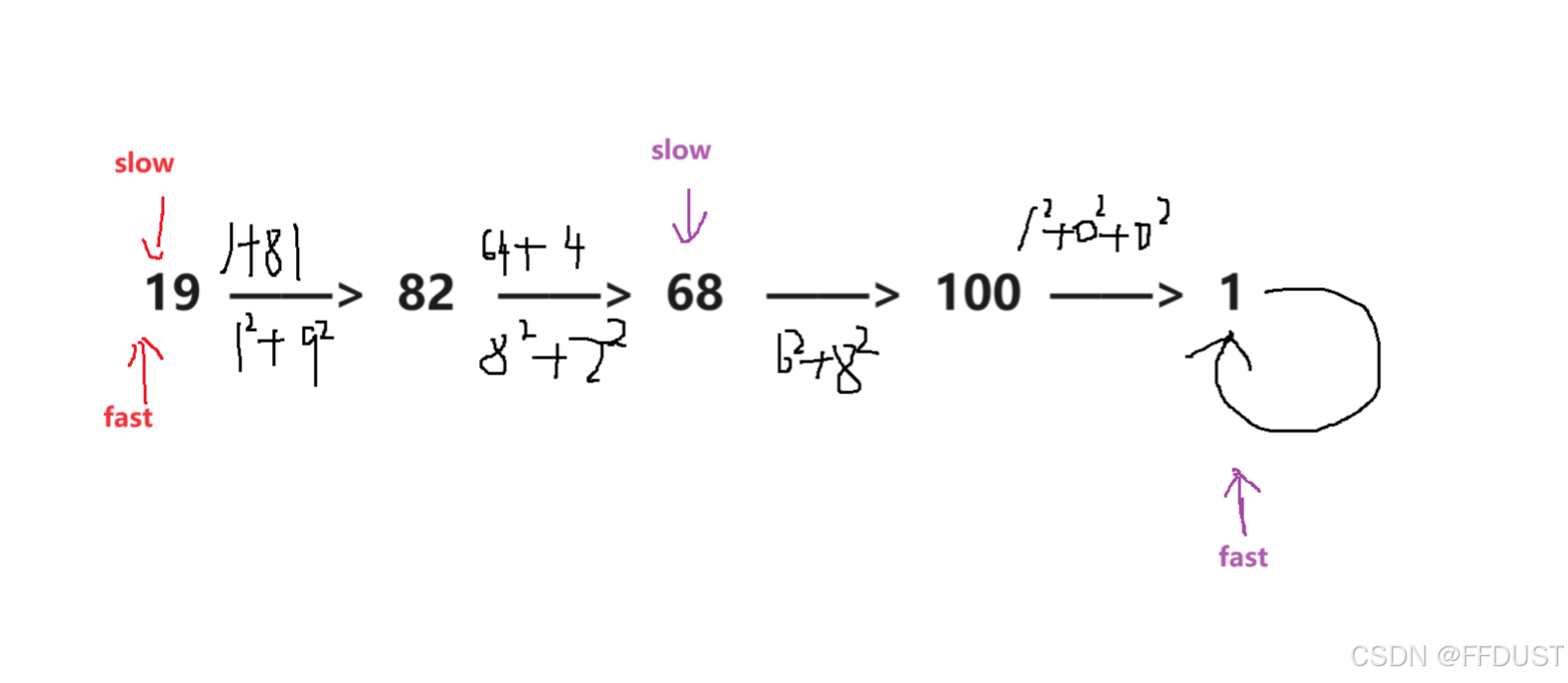
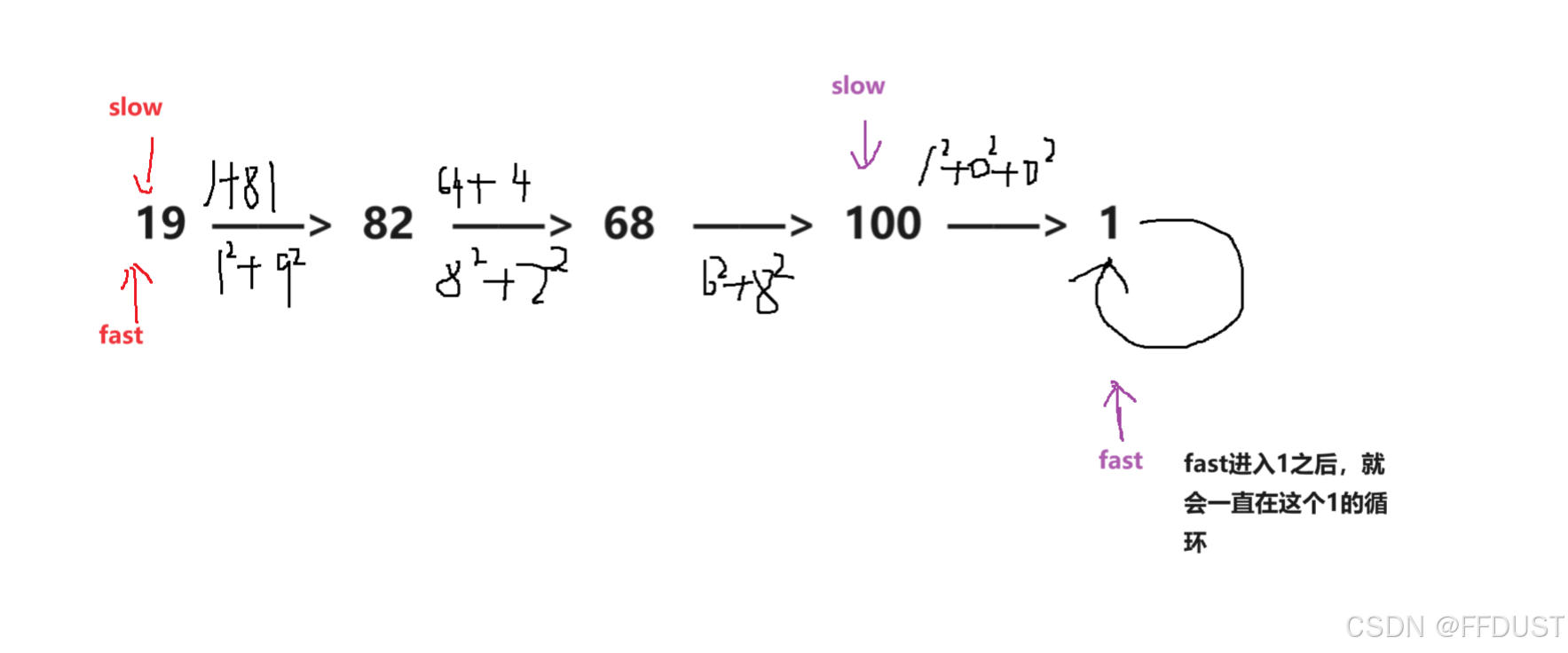
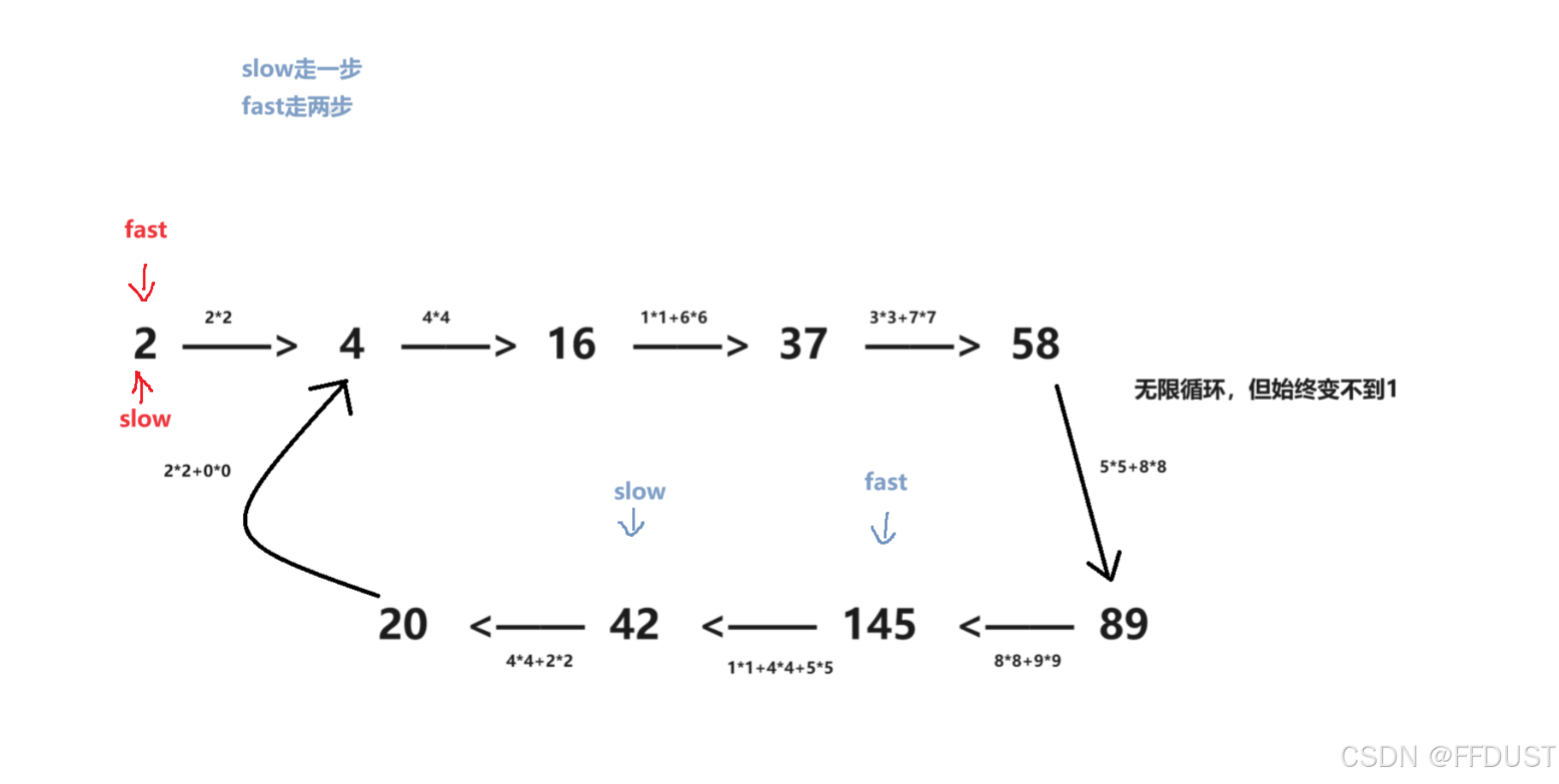
 根据题目可知：快乐数就是对于一个数，它的每位上的数字的平方和，最终结果是到1。

 2. 算法原理

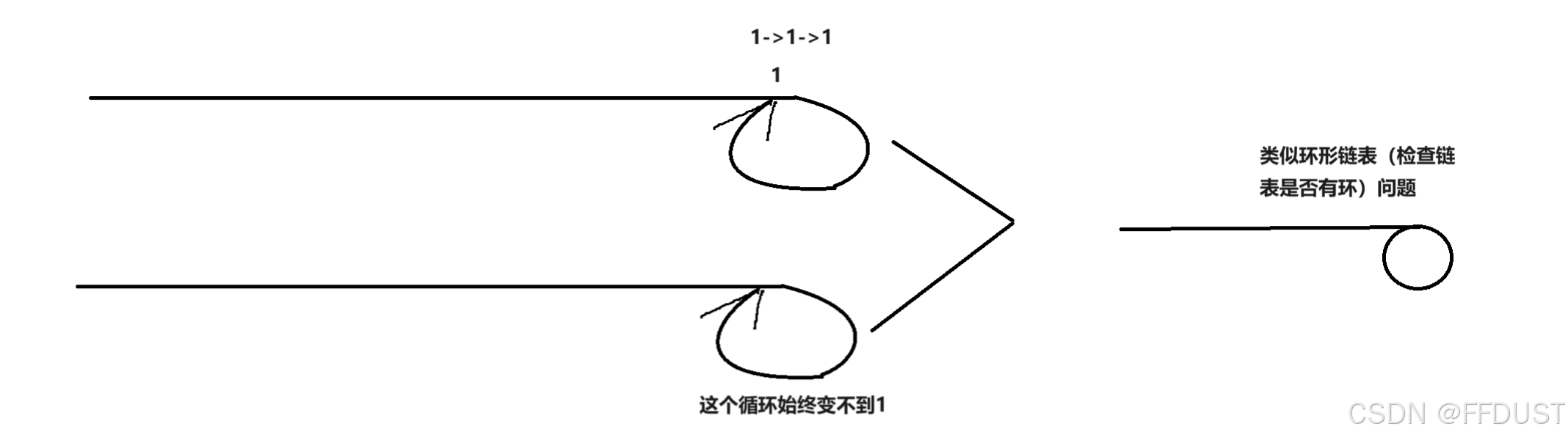
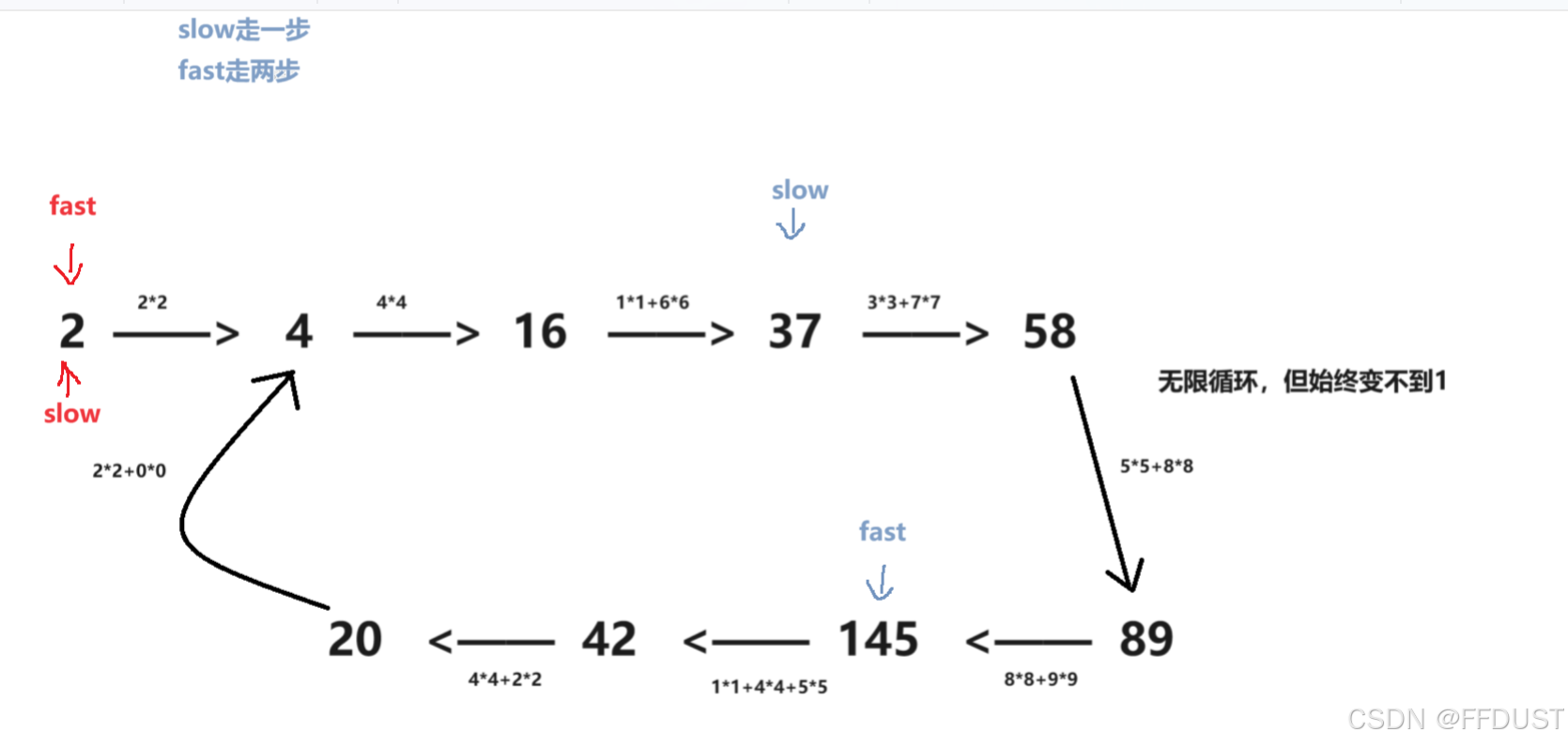
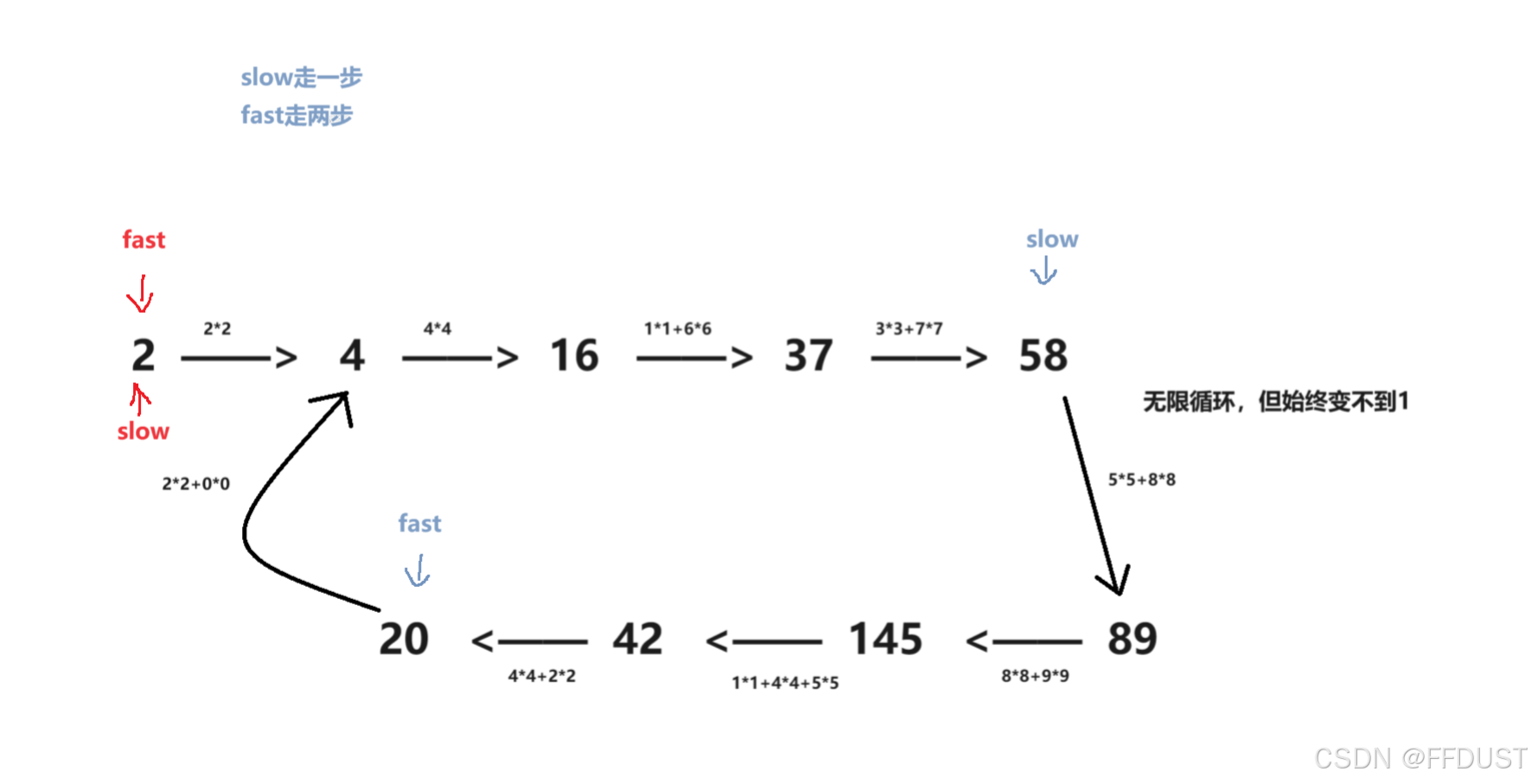
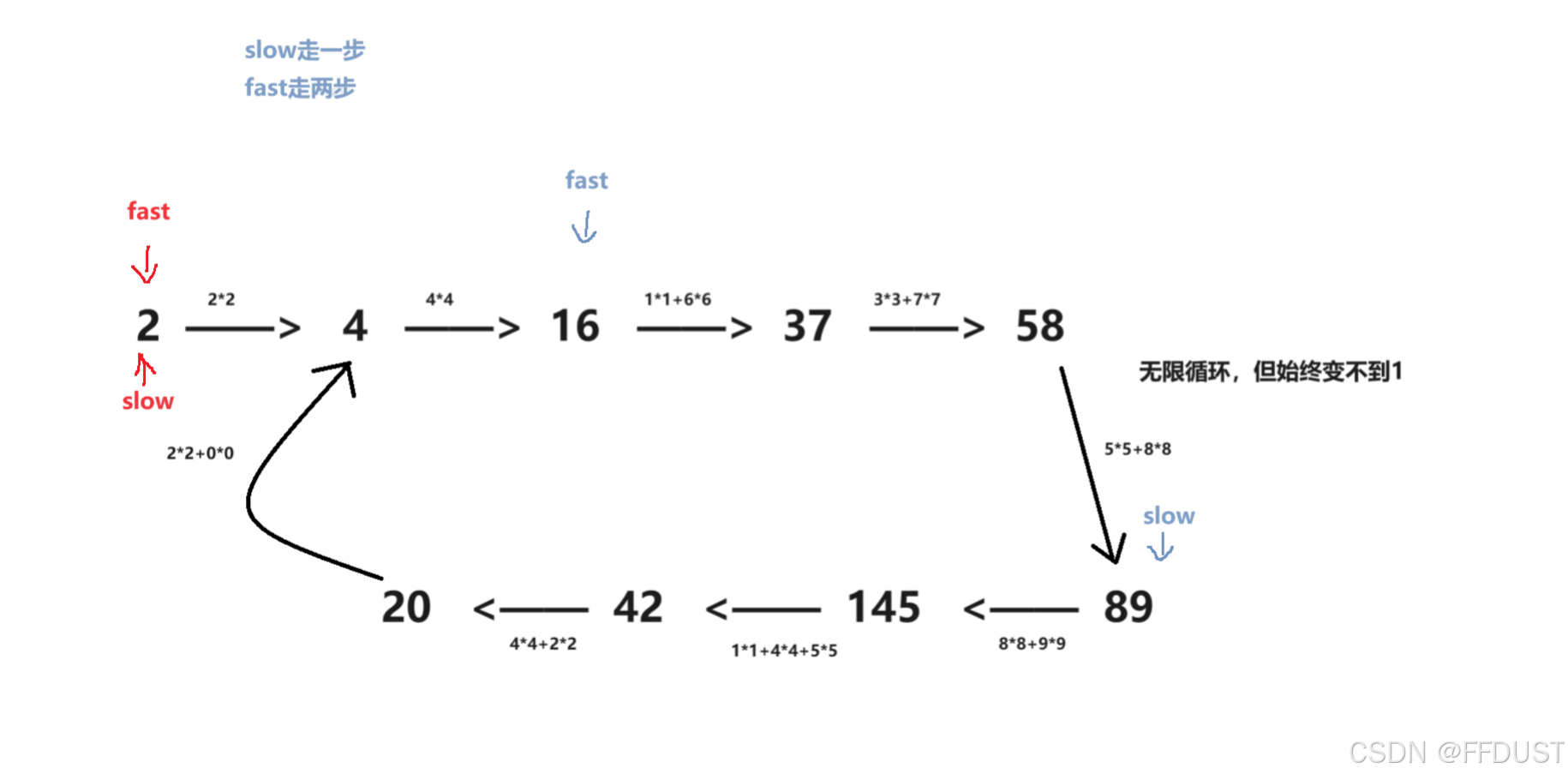
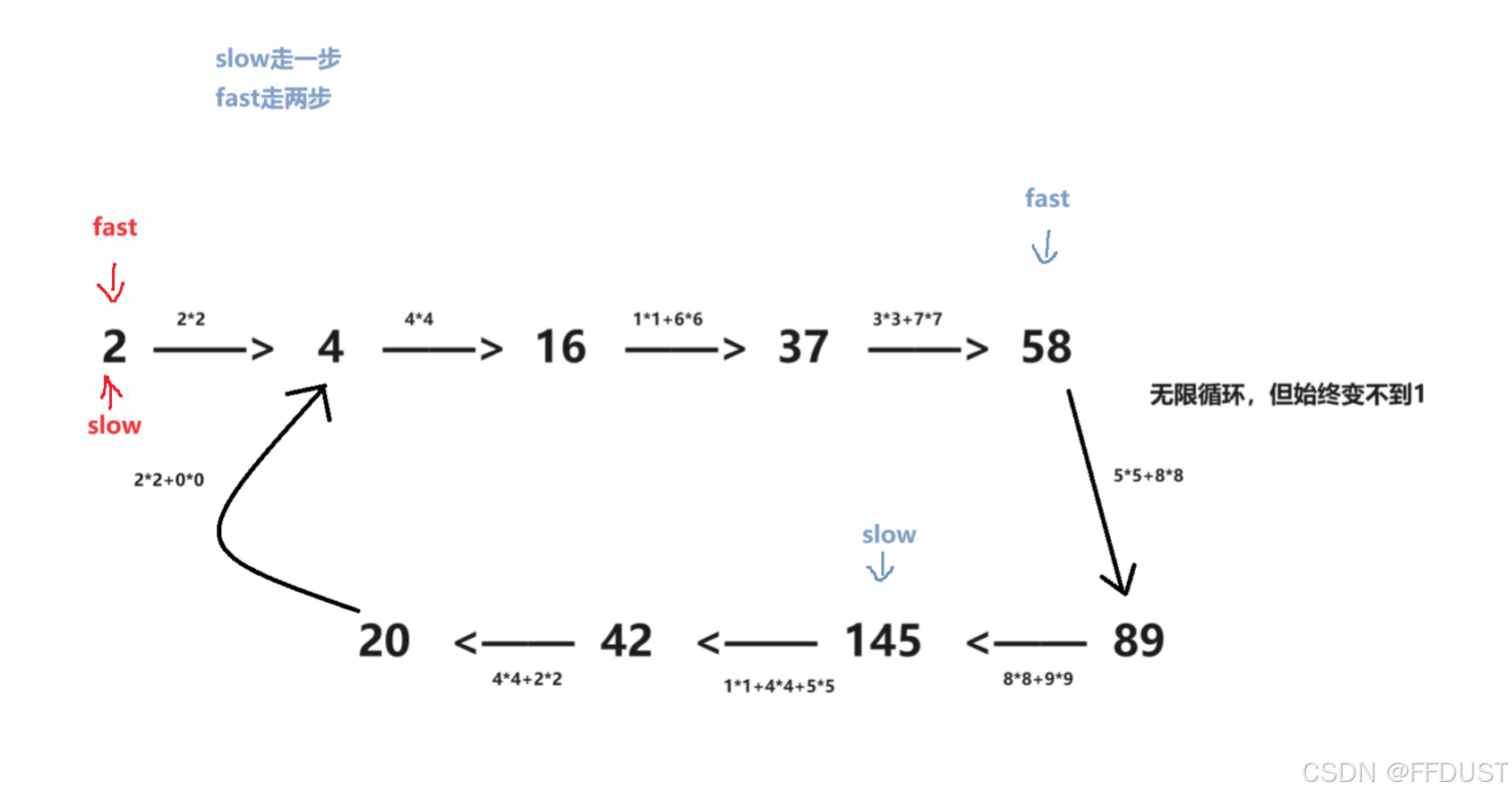
从题目解析上两个图对比来看

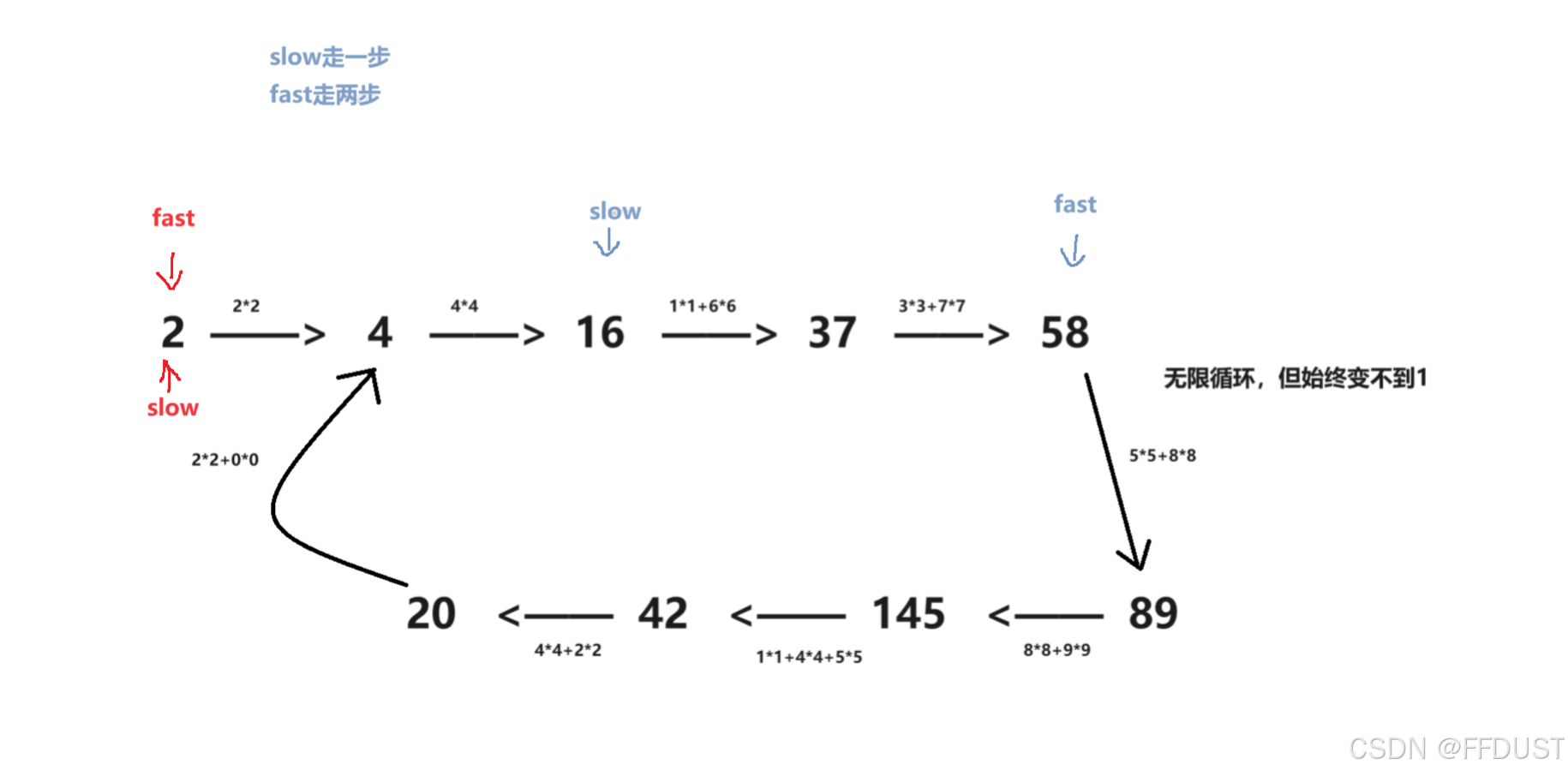
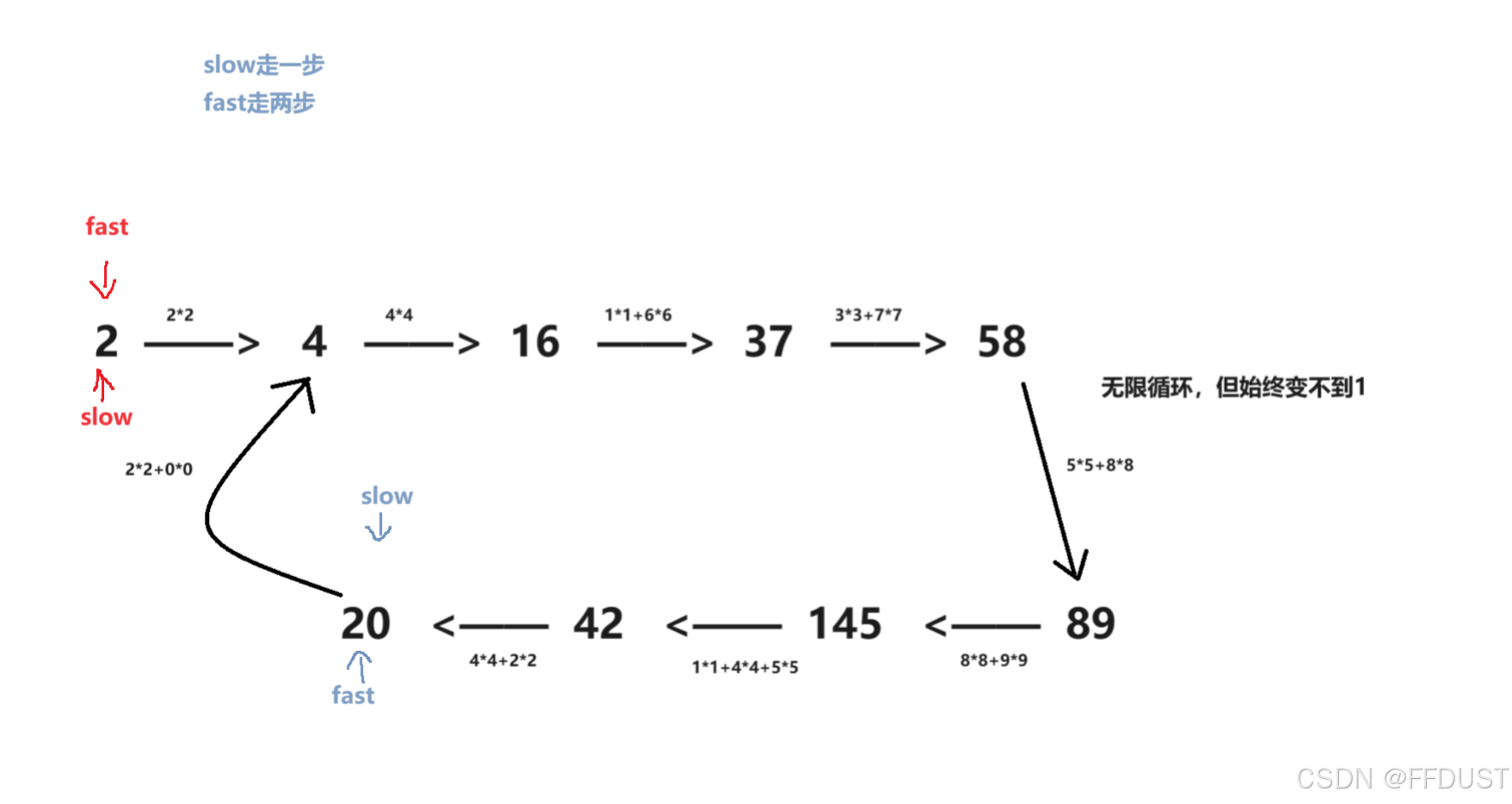
所以可以抽象成环形链表的问题，解法就用快慢双指针。（注：这里双指针是一种思想，并不是真正意义上要定义两个指针，用一个数看作成一个指针来控制）

解法思想：

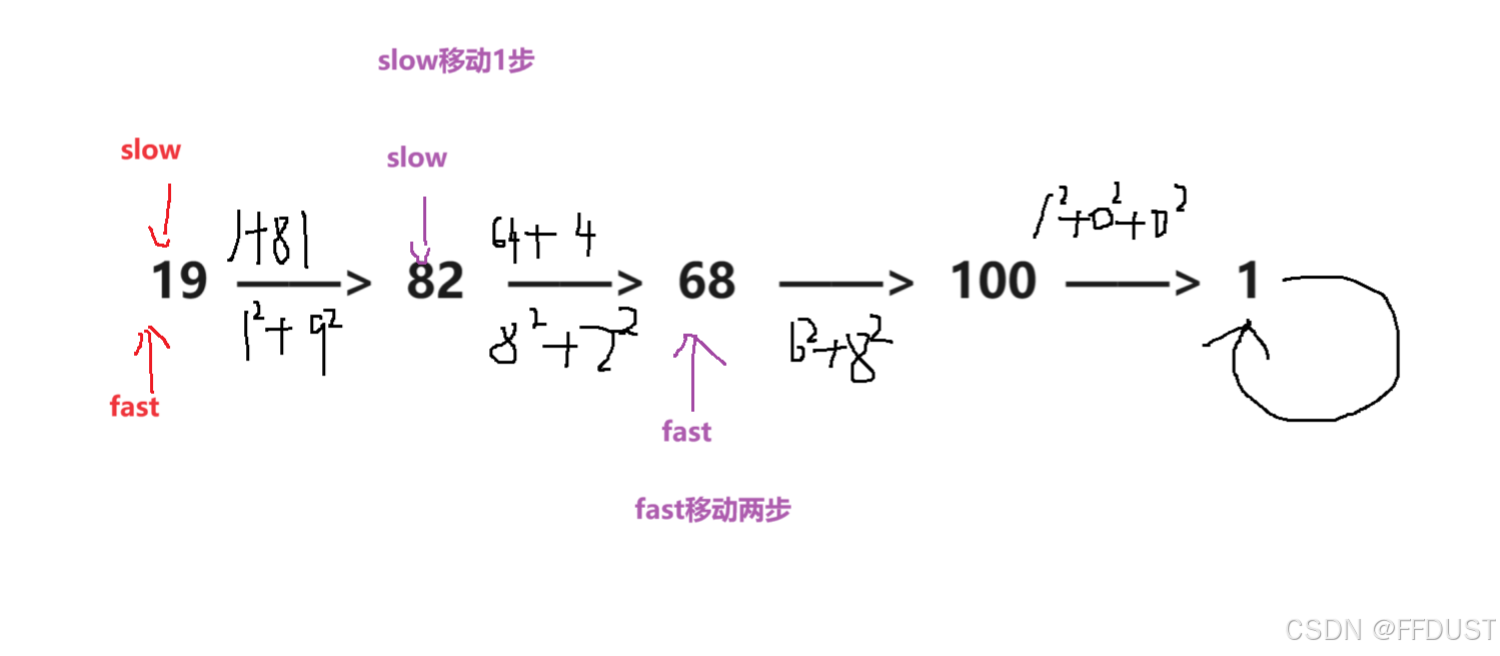
1. 定义快慢指针(fast,slow)
2. 慢指针每次向后移动一步，快指针每次向后移动两步。
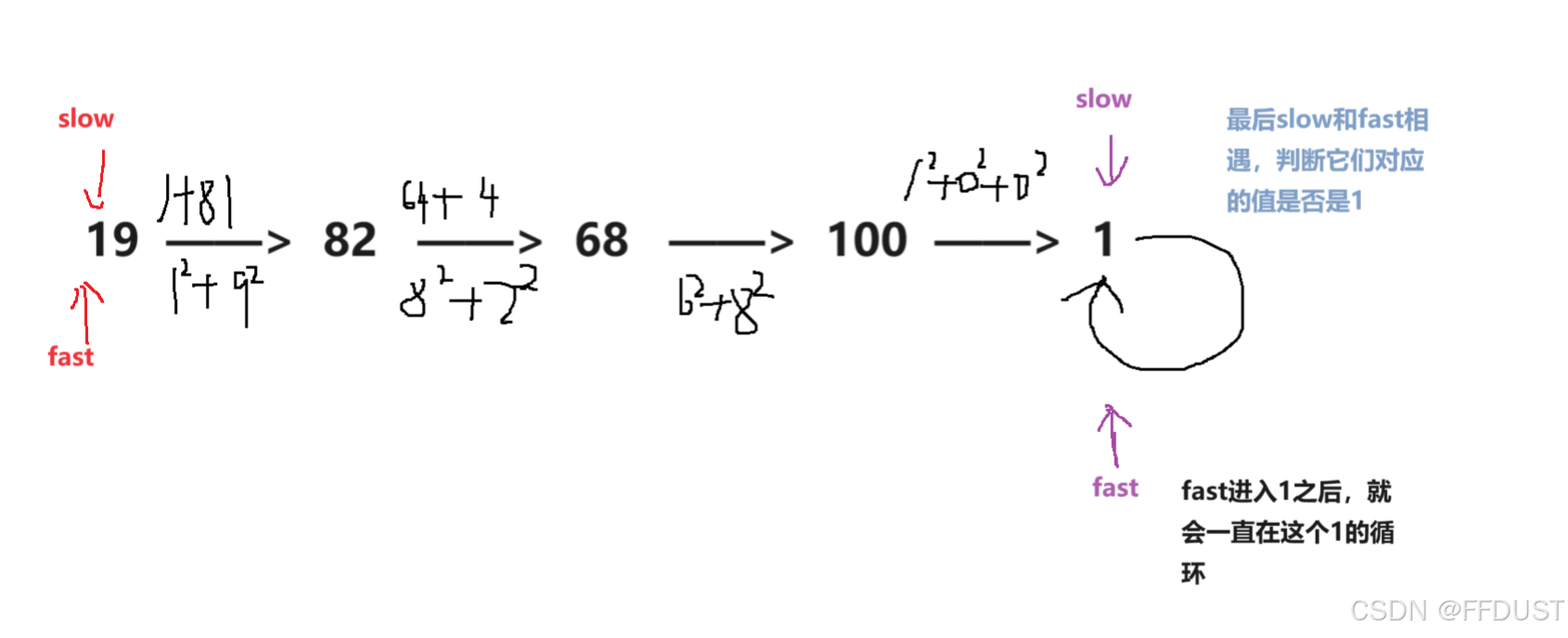
3. 判断相遇时的值即可，是1就是快乐数，不是1就不是快乐数（注：通过题目给予的定义来看是一定会相遇的）。

题外话：快慢双指针解决环形链表时，是通过判断两个指针是否相遇即可。 

为快乐数的情况：

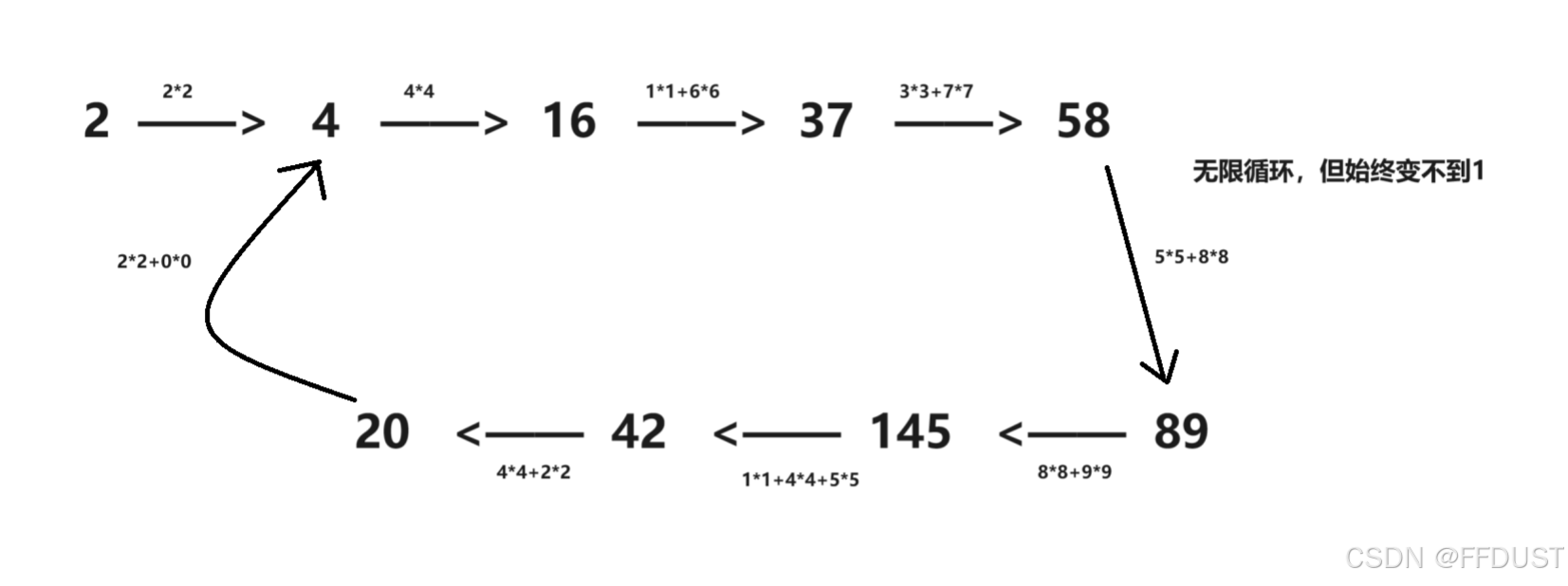
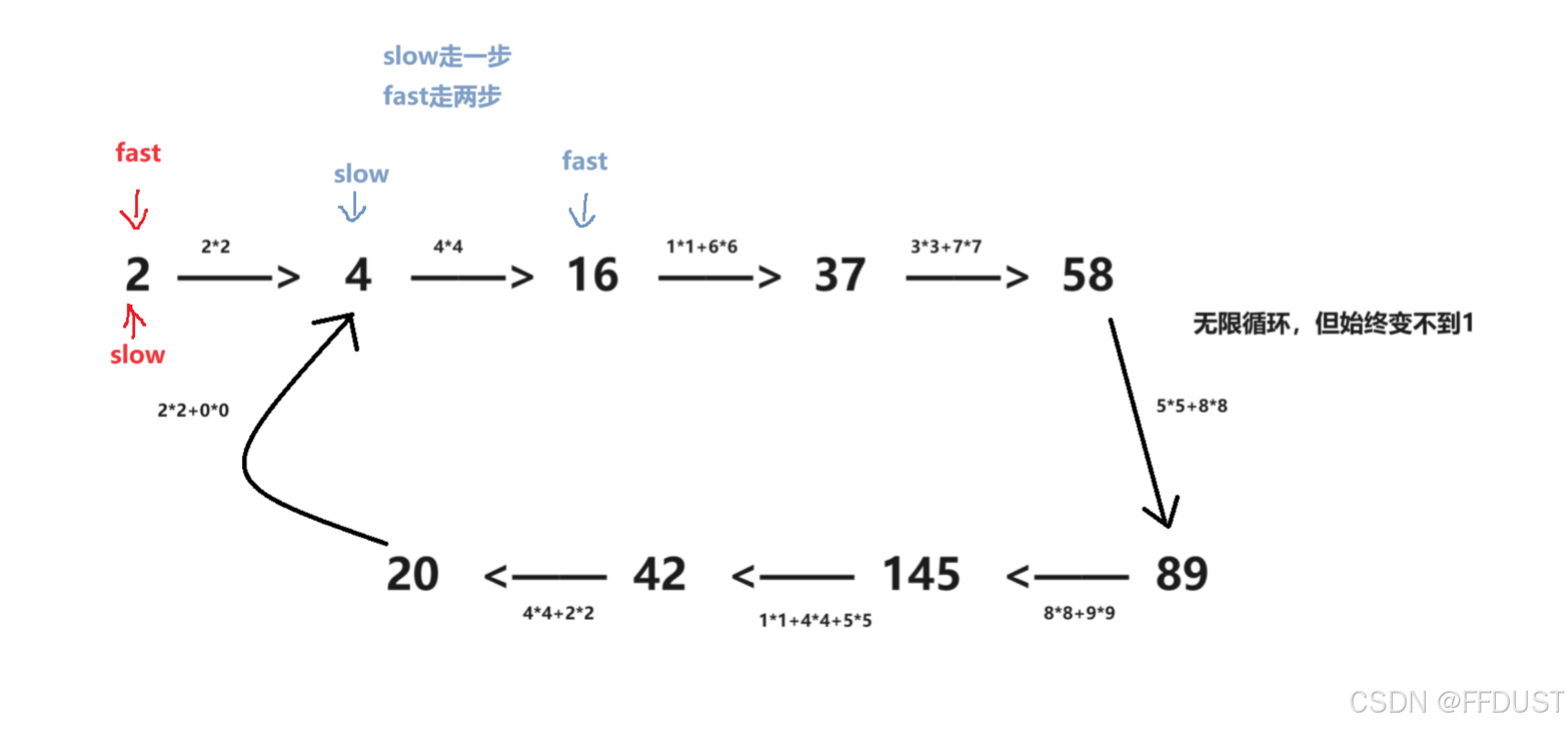
 不为快乐数的情况：

3. 代码实现

 根据上述分析：

class Solution {
public:
    //求平方和后续会用的频繁
    //因此把它封装到类里面，默认内联函数
    //减少函数调用的开销
    int bitSum(int n) // 返回n这个数的每一位数的平方相加的和
    {
        int sum = 0;
        // 先把最后一个数取出来，平方一下放到一个变量里，然后干掉最后一位数
        while (n) {
            int t = n % 10;
            sum += t * t;
            n /= 10;
        }

        return sum;
    }

    bool isHappy(int n) {
        // 抽象成快慢指针的解法
        int fast = bitSum(n), slow = n;  
        //因为一定是会相遇的，
        //先让fast走一步，以防止进入不了while循环
        while (slow != fast) {
            //fast要比slow快
            slow = bitSum(slow);
            fast = bitSum(bitSum(fast));
        }
        return slow == 1;   //返回判断是否等于1
    }
};

链接跳转：快乐数

提交记录：

制作不易,若有不足之处或出问题的地方，请各位大佬多多指教 ，感谢大家的阅读支持！！！