欢迎各位大佬们来到Tubishu的博客🌟
Tubishu是一名计算机本科生,不定期发送一些在学校的成果供佬们消遣~希望能为佬的编程之路添砖加瓦⭐🔥
求各位大佬们垂怜🔥点赞评论一下呗🔥🔥
本文专栏 ➡️ 数据结构
排序
本实验是基于C实现对一组数据进行排序,包括直接插入排序、折半插入排序、希尔排序、冒泡排序、快速排序、简单选择排序、堆排序和2-路归并排序这5种排序算法。
实验目的:
- 掌握各种排序算法的基本思想
- 掌握各种排序算法的实现方法
实验内容:
对一组数据进行排序,可选择直接插入排序、折半插入排序、希尔排序、冒泡排序、快速排序、简单选择排序、堆排序和2-路归并排序中的任意5种排序算法实现。
要求:设计菜单,根据菜单提示进行操作。
实验产出:
1.实验原理:
排序算法是将一组数据按照特定顺序排列的方法。常见的排序算法包括:
冒泡排序:通过重复交换相邻未按顺序排列的元素。
选择排序:每次从未排序部分选择最小元素放到已排序部分的末尾。
插入排序:构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
快速排序:通过一趟排序将待排序序列分割成两部分,其中一部分的所有元素都比另一部分小,然后递归地排序两部分。
归并排序:将数组分成两部分,分别排序后再合并。
2.核心代码:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
#define MAXSIZE 100 // 顺序表最大长度
typedef int KeyType; // 定义关键字类型为整型
typedef int InfoType; // 定义其他数据项类型
typedef struct { // 定义每个记录(数据元素)的结构
KeyType key ; // 关键字项
InfoType otherinfo; // 其他数据项
} RedType; // 记录类型
typedef struct { // 定义顺序表的结构
RedType r[MAXSIZE+1]; // 存储顺序表,r[0]闲置、缓存或用作哨兵单元
int length; // 顺序表的长度
} SqList;
// 直接插入排序
void InsertSort(SqList &L)
{ // 对顺序表L做直接插入排序
for (int i=2; i<=L.length; i++) {
if ( L.r[i].key < L.r[i-1].key ) { // 将L.r[i]插入有序子表
L.r[0]=L.r[i]; // 将L.r[0]看作监视哨,将待插入的记录暂存到此处
L.r[i]=L.r[i-1]; // 将r[i-1]后移
int j=0;
for(j=i-2; L.r[0].key<L.r[j].key; --j) // 从后向前寻找插入位置
L.r[j+1]=L.r[j]; // 记录逐个后移,直到找到插入位置
L.r[j+1]=L.r[0]; // 将r[0]即原r[i],插入到正确位置
}
}
}
// 折半插入排序
void BInsertSort (SqList &L )
{ // 对顺序表L做折半插入排序
int low, high, m;
for (int i=2; i<= L.length ; ++i ) {
L.r[0] = L.r[i]; // 将待插入的记录暂时存到监视哨中
low = 1 ; high = i-1 ; // 置查找区间初值
while ( low <= high ) { // 在r[low..high]中折半查找插入的位置
m = ( low + high ) / 2 ; // 折半
if ( L.r[0].key < L.r[m]. key ) high = m -1; //插入点在前一子表
else low = m + 1; // 插入点在后一子表
}
for (int j=i-1; j>=high+1; --j )
L.r[j+1] = L.r[j]; // 记录后移
L.r[high+1] = L.r[0]; // 将r[0]即原r[i]插入到正确位置
}
}
// 希尔排序
void ShellInsert(SqList &L, int dk)
{ // 对顺序表L做一趟增量是dk的希尔插入排序
for( int i=dk+1; i<=L.length; ++ i) {
if (L.r[i].key < L.r[i-dk].key) { // 需将L.r[i]插入有序增量子表
L.r[0]=L.r[i]; // 暂存在L.r[0]
int j=0;
for(j=i-dk; j>0 &&(L.r[0].key<L.r[j].key); j-=dk)
L.r[j+dk]=L.r[j]; // 记录后移,直到找到插入位置
L.r[j+dk]=L.r[0];
}
}
}
void ShellSort(SqList &L)
{ // 按增量序列dt[ ]对顺序表L作Shell排序
int dt[5]={11,7,5,1}, t=4;
for (int k=0; k<t; ++k)
ShellInsert(L, dt[k]); // 增量为dt[k]的希尔插入排序
}
// 冒泡排序
void BubbleSort(SqList &L)
{ // 对顺序表L做冒泡排序
int m,j,flag=1;
RedType x;
m=L.length-1;
while(m>0 && flag) {
flag=0; // flag置为0,如果本趟排序没有发生交换,则不会执行下一趟排序
for(j=1; j<=m; j++) {
if (L.r[j].key>L.r[j+1].key) {
flag=1; // flag置为1,表示本趟排序发生了交换
x=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=x; // 交换前后两个记录
}
}
m--;
}
}
// 快速排序
void QuickSort(SqList &L, int low, int high)
{
int left=low, right=high;
RedType temp=L.r[low]; // 用子表的第一个记录做枢轴记录
while (low<high) { // 从表的两端交替地向中间扫描
while((L.r[high].key >= temp.key) && (low<high)) high--;
if (low<high) L.r[low++].key=L.r[high].key; // 将比枢轴记录小的记录移到低端
while((L.r[low].key<=temp.key) && (low<high)) low++;
if (low<high) L.r[high--].key=L.r[low].key; // 将比枢轴记录大的记录移到高端
}
L.r[low]=temp; // 一次划分得到枢轴记录的正确位置,存枢轴记录
if(left<low-1) QuickSort(L,left,low-1); // 递归调用,排序左子表
if(low+1<right)QuickSort(L,low+1,right); // 递归调用,排序右子表
}
// 简单选择排序
void SelectSort(SqList &L)
{ // 对顺序表L做简单选择排序
int i, j, k;
for (i=1; i<L.length; i++) { // 做第i趟排序(1≤i≤L.length-1)
k=i;
for (j=i+1; j<=L.length; j++) // 在当前无序区L.r[j]...L.r[L.length]中选关键
// 字最小的记录L.r[k]
if (L.r[j].key < L.r[k].key)
k=j; // k记下目前找到的最小关键字所在的位置
if (k!=i) { // 交换L.r[i]和L.r[k]
L.r[0]=L.r[i];
L.r[i]=L.r[k];
L.r[k]=L.r[0]; // L.r[0]作暂存单元
} // endif
} // endfor
} // SeleetSort
// 堆排序
void HeapAdjust(SqList &L, int s, int m)
{ // 本算法以大根堆为例
// 假设L.r[s+1]…L.r[m]已经是堆,将L.r[s]…L.r[m]调整为以L.r[s]为根的大根堆
RedType rc=L.r[s];
for (int j=2*s; j<=m; j*=2) { // 沿关键字较大的子结点向下筛选
if (j<m && L.r[j].key<L.r[j+1].key)
j++; // j为关键字较大的记录的下标
if (rc.key >= L.r[j].key) break; // 满足堆条件,退出
L.r[s]=L.r[j]; s=j; // 使s结点满足堆定义,再求子树j是否满足堆条件
}
L.r[s]=rc; // 插入
}
// 建堆
void CreatHeap(SqList &L)
{ // 把无序序列L.r[1]…L.r[n]建成一个大根堆
int n=L.length;
for (int i=n/2; i>0; --i) // 反复调用HeapAdjust建堆
HeapAdjust(L,i,n);
}
// 堆排序
void HeapSort(SqList &L)
{ // 对顺序表L进行堆排序
RedType x;
CreatHeap(L); // 建堆
for(int i=L.length; i>1; i--) {
x=L.r[1]; // 将堆顶记录和当前未经排序子序列L.r[2]…L.r[i]中最后一个记录互换
L.r[1] = L.r[i];
L.r[i] =x;
HeapAdjust(L, 1, i-1); // 将元素L.r[1]...L.r[i-1]重新调整为堆
}
}
// 归并排序
void Merge (SqList &R, SqList &T, int low, int mid, int high)
{ // 将有序表R.r[low]…R.r[mid]和R.r[mid+1]…R.r[high]归并为有序表T.r[low]..T.r[high]
int i=0;
int j=0;
int k=0;
for (i=low, j=mid+1, k=low; i<=mid && j<=high; k++) {
if (R.r[i].key<=R.r[j].key) T.r[k]=R.r[i++]; // 将R中记录由小到大并入T中
else T.r[k]=R.r[j++];
}
while (i<=mid) T.r[k++]=R.r[i++]; // 将剩余的元素R.r[i]..R.r[mid]复制到T中
while (j<=high) T.r[k++]=R.r[j++]; // 将剩余的元素R.r[j]..R.r[high]复制到T中
}
void MergeSort(SqList &R, SqList &T, SqList &S,int low, int high)
{ // R.r[low]…R.r[high]归并排序后存入T中,S仅用作临时存放数据元素
if (low==high) T.r[low]=R.r[low];
else {
int mid=(low+high)/2; // 将当前序列一分为二,求出分裂点mid
MergeSort(R,S,T,low,mid); // 对子序列R.r[low]..R.r[mid]归并排序,
// 结果放入S.r[low]..S.r[mid]
MergeSort(R,S,T,mid+1,high); // 对子序列R.r[mid+1]..R.r[high]归并排序,
// 结果放入S.r[mid+1]..S.r[high]
Merge(S,T,low,mid,high); // 将S.r[low]..S.r[mid]和S.r[mid+1]..S.r[high]
// 归并到T.r[low]..T.r[high]
}
}
void print(SqList R)
{
for(int i=1; i<=R.length; i++){
if((i-1)%10==0) printf("\n");
printf("%6d", R.r[i].key);
}
printf("\n");
}
void producerandom(SqList &T)
{
srand(time(NULL)); // time()返回从某点开始到现在的秒数,设置随机种子。
for(int i=1; i<=MAXSIZE; i++)
T.r[i].key = rand()%1000; // 产生0-1000之间的随机数
T.length=MAXSIZE;
print(T); // 输出随机数
}
// 显示菜单
void showmenu()
{
printf("\n\n");
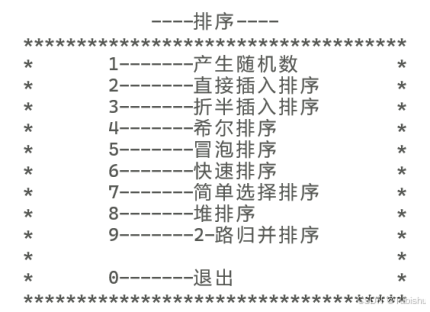
printf("\t ----排序---- \n");
printf("\t************************************\n");
printf("\t* 1-------产生随机数 *\n");
printf("\t* 2-------直接插入排序 *\n");
printf("\t* 3-------折半插入排序 *\n");
printf("\t* 4-------希尔排序 *\n");
printf("\t* 5-------冒泡排序 *\n");
printf("\t* 6-------快速排序 *\n");
printf("\t* 7-------简单选择排序 *\n");
printf("\t* 8-------堆排序 *\n");
printf("\t* 9-------2-路归并排序 *\n");
printf("\t* *\n");
printf("\t* 0-------退出 *\n");
printf("\t************************************\n");
}
void Sort()
{
SqList R,T,S; // T存放原始数据,R存放排序后的数据,S临时变量
char choice = 'N';
int randfl = 0; // 随机数产生标志,0 无,1有
while(choice!='0')
{
printf("\n请选择菜单号(0--9): ");
scanf("%c",&choice); getchar(); // clear '\n'
switch (choice)
{
case '1':
printf("\n\t产生随机数......\n");
producerandom(T);
randfl = 1; // 随机数已产生
break;
case '2':
if (randfl == 0)
printf("\n\t 请先产生随机数\n");
else {
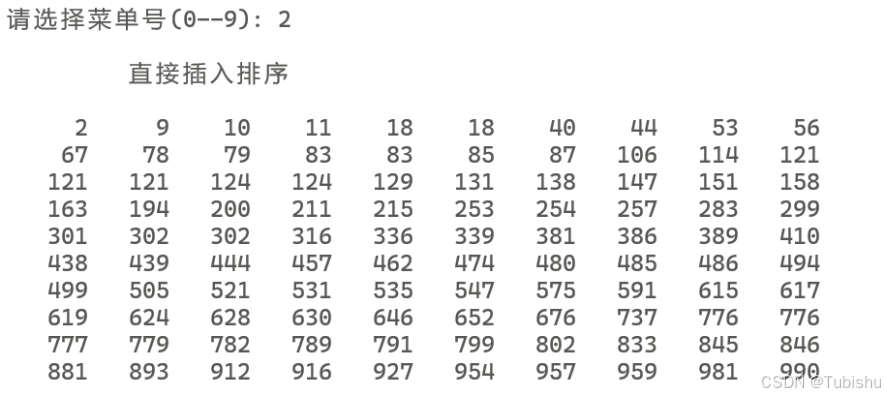
printf("\n\t 直接插入排序\n");
R=T; // 将T复制给R,使R等于原始数据
InsertSort(R);
print(R);
}
break;
case '3':
if (randfl == 0)
printf("\n\t 请先产生随机数\n");
else {
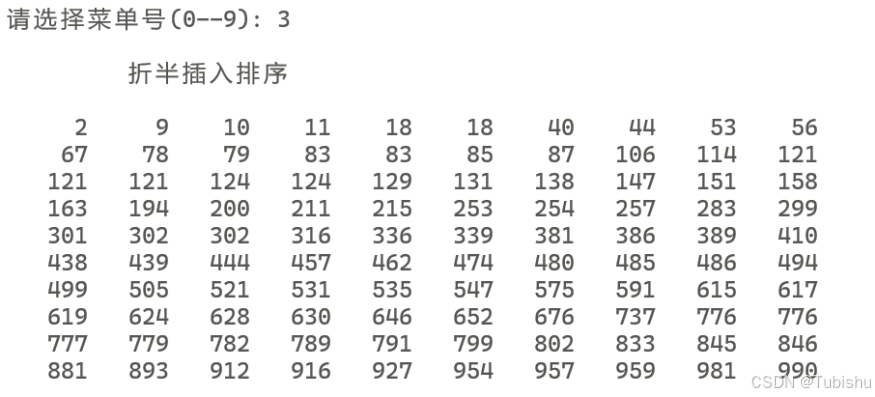
printf("\n\t 折半插入排序\n");
R=T; // 将T复制给R,使R等于原始数据
BInsertSort(R);
print(R);
}
break;
case '4':
if (randfl == 0)
printf("\n\t 请先产生随机数\n");
else {
printf("\n\t 希尔排序\n");
R=T; // 将T复制给R,使R等于原始数据
ShellSort(R);
print(R);
}
break;
case '5':
if (randfl == 0)
printf("\n\t 请先产生随机数\n");
else {
printf("\n\t 冒泡排序\n");
R=T; // 将T复制给R,使R等于原始数据
BubbleSort(R);
print(R);
}
break;
case '6':
if (randfl == 0) {
printf("\n\t 请先产生随机数\n");
}else {
printf("\n\t 快速排序\n");
R=T; // 将T复制给R,使R等于原始数据
QuickSort(R, 1, R.length);
print(R);
}
break;
case '7':
if (randfl == 0) {
printf("\n\t 请先产生随机数\n");
}else {
printf("\n\t 简单选择排序\n");
R=T; // 将T复制给R,使R等于原始数据
SelectSort(R);
print(R);
}
break;
case '8':
if (randfl == 0) {
printf("\n\t 请先产生随机数\n");
}else {
printf("\n\t 堆排序\n");
R=T; // 将T复制给R,使R等于原始数据
HeapSort(R);
print(R);
}
break;
case '9':
if (randfl == 0) {
printf("\n\t 请先产生随机数\n");
}else {
printf("\n\t 归并排序\n");
R=T; // 将T复制给R,使R等于原始数据
S=T;
MergeSort(R,R,S,1,R.length);
print(R);
}
break;
case '0':
printf("\n\t 程序结束!\n");
break;
default:
printf("\n\t 输入错误,请重新输入!\n");
}
}
}
int main()
{
showmenu();
Sort();
return 0;
}
3.运行结果:
其他的排序结果赶快去用代码实操看看叭
4.调试:
未生成随机数直接排序:
5.性能分析:
1.时间复杂度分析
时间复杂度是衡量算法运行时间随数据规模增长而增长的速率。
1.1冒泡排序
平均时间复杂度:O(n²)
最坏时间复杂度:O(n²)
最好时间复杂度:O(n)(当数据已经有序时)
稳定性:稳定
分析:
冒泡排序通过重复比较相邻元素并交换它们来实现排序。在最坏情况下,每对元素都需要交换,导致时间复杂度为O(n²)。在最好情况下,数据已经有序,只需进行一次遍历,时间复杂度为O(n)。
实验结果:
在实验中,冒泡排序在处理大规模数据时表现不佳。
1.2选择排序
平均时间复杂度:O(n²)
最坏时间复杂度:O(n²)
最好时间复杂度:O(n²)
稳定性:不稳定
分析:
选择排序每次从未排序部分选择最小元素放到已排序部分的末尾。无论数据是否有序,选择排序都需要进行n(n-1)/2次比较,因此时间复杂度始终为O(n²)。
实验结果:
选择排序在处理大规模数据时性能较差。
1.3插入排序
平均时间复杂度:O(n²)
最坏时间复杂度:O(n²)
最好时间复杂度:O(n)(当数据已经有序时)
稳定性:稳定
分析:
插入排序通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。在最好情况下,数据已经有序,只需进行一次遍历,时间复杂度为O(n)。在最坏情况下,每插入一个元素都需要移动所有已排序元素,时间复杂度为O(n²)。
实验结果:
插入排序在处理小规模数据时表现良好,但在处理大规模数据时性能下降。
1.4快速排序
平均时间复杂度:O(n log n)
最坏时间复杂度:O(n²)(当枢轴选择不当,如数据已经有序时)
最好时间复杂度:O(n log n)
稳定性:不稳定
分析:
快速排序通过一趟排序将待排序序列分割成两部分,其中一部分的所有元素都比另一部分小,然后递归地排序两部分。在平均情况下,时间复杂度为O(nlogn)。在最坏情况下,如数据已经有序且枢轴选择不当,时间复杂度退化为O(n²)。
实验结果:
快速排序在处理大规模数据时表现最佳。
1.5归并排序
平均时间复杂度:O(nlogn)
最坏时间复杂度:O(nlogn)
最好时间复杂度:O(nlogn)
稳定性:稳定
分析:
归并排序将数组分成两部分,分别排序后再合并。由于每次递归都将数组分成两半,因此时间复杂度始终为O(nlogn)。归并排序需要额外的空间来存储合并后的数组。
实验结果:
归并排序在处理大规模数据时性能稳定。
2.空间复杂度分析
空间复杂度是衡量算法运行过程中临时占用存储空间大小的指标。
2.1冒泡排序、选择排序、插入排序
空间复杂度:O(1)(原地排序)
分析:
这三种排序算法都是原地排序,不需要额外的存储空间。
2.2快速排序
空间复杂度:O(logn)(递归调用栈)
分析:
快速排序在递归调用时需要使用栈空间。在平均情况下,空间复杂度为O(logn)。
2.3归并排序
空间复杂度:O(n)(需要额外的数组存储合并结果)
分析:
归并排序需要额外的空间来存储合并后的数组,空间复杂度为O(n)。
3.性能对比总结
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 稳定性 | 空间复杂度 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(n²) | O(n) | 稳定 | O(1) |
| 选择排序 | O(n²) | O(n²) | O(n²) | 不稳定 | O(1) |
| 插入排序 | O(n²) | O(n²) | O(n) | 稳定 | O(1) |
| 快速排序 | O(n log n) | O(n²) | O(n log n) | 不稳定 | O(log n) |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | 稳定 | O(n) |
总结
(1)掌握了各种排序算法的基本思想;
(2)掌握了各种排序算法的实现方法。
快速排序在实验中表现最佳,验证了其在平均情况下的高效性。
冒泡排序和选择排序在处理大规模数据时效率较低,符合理论预期。
插入排序在处理小规模数据时表现良好,但在处理大规模数据时性能下降。
归并排序虽然性能稳定,但需要额外的空间,实验中需要考虑内存使用情况。
佬~来都来了 点个赞👍、评论一下💬呗🥺你的支持是Tubishu不断前行的源泉✨!衷心感谢你的鼓励与陪伴🙏!
愿各位大佬们在技术的道路上,代码顺畅无阻💻,思路清晰如光💡,不断突破自我,向着更高的目标迈进,实现自己的梦想!🎉
再次感谢大佬的莅临🌸