前言

提醒：
文章内容为方便作者自己后日复习与查阅而进行的书写与发布，其中引用内容都会使用链接表明出处（如有侵权问题，请及时联系）。
其中内容多为一次书写，缺少检查与订正，如有问题或其他拓展及意见建议，欢迎评论区讨论交流。

分类与回归算法

机器学习中的分类与回归算法是两种主要的监督学习任务，它们分别用于解决不同类型的问题。以下是这两种算法的总结：

1. 分类算法：
   分类算法用于将数据分成不同的类别，适用于输出为离散标签的问题。常见的分类算法包括：

   1. 逻辑回归：使用逻辑函数来估计概率，用于二分类问题，也可以扩展到多分类问题。
   2. 支持向量机（SVM）：通过找到最优的决策边界来最大化样本的分类准确率，适用于高维数据。
   3. 决策树：通过树结构来进行决策，每个节点代表一个特征的选择，叶子节点代表分类结果。
   4. 随机森林：由多个决策树组成的集成学习方法，通过投票来决定最终分类结果。
   5. 梯度提升决策树（GBDT）：通过构建和结合多个弱学习器来形成强学习器，适用于分类和回归问题。
   6. 朴素贝叶斯：基于贝叶斯定理，假设特征之间相互独立，适用于文本分类等场景。
   7. K近邻（KNN）：根据样本之间的距离进行分类，适用于小规模数据集。
   8. 神经网络：通过多层感知机学习数据的复杂模式，适用于图像、语音等复杂分类问题。

2. 回归算法：
   回归算法用于预测连续数值输出，适用于输出为连续变量的问题。常见的回归算法包括：

   1. 线性回归：通过拟合一条直线来预测目标变量的值，是最简单的回归方法。
   2. 岭回归：线性回归的扩展，通过引入L2正则化项来防止过拟合。
   3. Lasso回归：线性回归的另一种扩展，通过引入L1正则化项来进行特征选择。
   4. 弹性网回归：结合了岭回归和Lasso回归，同时引入L1和L2正则化项。
   5. 决策树回归：使用决策树结构来进行回归预测，适用于非线性关系。
   6. 随机森林回归：由多个决策树组成的集成学习方法，通过平均来决定最终回归结果。
   7. 梯度提升决策树回归（GBDT回归）：通过构建和结合多个弱学习器来形成强学习器，适用于回归问题。
   8. 支持向量回归（SVR）：支持向量机在回归问题上的应用，通过找到最优的决策边界来最大化样本的回归准确率。
   9. 神经网络回归：通过多层感知机学习数据的复杂模式，适用于复杂的回归问题。

3. 分类与回归算法的比较：

   • 输出类型：分类算法输出离散标签，回归算法输出连续数值。
   • 评估指标：分类算法常用准确率、召回率、F1分数等指标，回归算法常用均方误差（MSE）、均方根误差（RMSE）等指标。
   • 问题类型：分类算法适用于类别预测问题，如垃圾邮件检测；回归算法适用于数值预测问题，如房价预测。 在实际应用中，选择分类还是回归算法取决于问题的性质和需求。有时，可以将回归问题转化为分类问题，或者将分类问题转化为回归问题，具体取决于问题的特点和目标。

支持向量回归（SVR）数学原理

支持向量机（分类算法）可参见：python_支持向量机（SVM）

支持向量回归（Support Vector Regression，简称SVR）是支持向量机（Support Vector Machine，简称SVM）在回归问题上的应用。SVR的目标是找到一个函数f(x)，使得f(x)与实际输出y之间的差异不超过ε，同时不存在误判。SVR通过引入ε不敏感损失函数来处理回归问题。
在SVR中，我们使用ε不敏感损失函数来衡量预测值与实际值之间的差异。该损失函数定义为：
$$L_{ϵ}(f(x)-y)=\max (0,|f(x)-y|-ϵ)$$
这意味着只有当预测值与实际值之间的差异超过ε时，才会计算损失。

1. 目标函数

SVR 通过最小化以下目标函数来实现这一目标：

$$\underset{w,b,\xi ,{\xi }^{\ast }}{\min }\left(\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^m({\xi }_i+{\xi }_i^{\ast })\right)$$

其中：

• $\Vert w{\Vert }^2$ 代表模型的复杂度。
• $C$ 是正则化参数，用于平衡复杂度和误差。
• ${\xi }_i$ 和 ${\xi }_i^{\ast }$ 是松弛变量，用于处理超出 $ϵ$ 范围的偏差。

2. 约束条件

目标函数受以下约束：

$$\{\begin{array}{l}{y}_i-⟨w,\varphi (x_i)⟩-b\le ϵ+{\xi }_i,\\ ⟨w,\varphi (x_i)⟩+b-y_i\le ϵ+{\xi }_i^{\ast },\\ {\xi }_i,{\xi }_i^{\ast }\ge 0\forall i.\end{array}$$

其中：

• $ϵ$ 是 $ϵ$-不敏感损失函数的阈值。
• $\varphi (x_i)$ 是输入特征向量 $x_i$ 的高维映射。
• $⟨w,\varphi (x_i)⟩$表示内积，又称为点积或标量积，是两个向量之间的一种运算，返回一个标量值。对于实向量空间 ${\mathbb{R}}^n$ 中的两个向量 $\mathbf{u}$ 和 $\mathbf{v}$，内积定义为：
  $$\mathbf{u}\cdot \mathbf{v}=\sum _{i=1}^n{u}_i{v}_i$$
  这表示将两个向量的对应分量相乘，然后将所有这些乘积相加。
  为了方便矩阵运算，内积也可以表示为：
  $$\mathbf{u}\cdot \mathbf{v}={\mathbf{u}}^T\mathbf{v}$$
  在函数空间 $L^2([a,b])$ 中，内积可以定义为积分形式。对于定义在区间 $[a,b]$ 上的两个函数 $f$ 和 $g$，内积表示为：
  $$⟨f,g⟩={\int }_a^{b}f(x)g(x)dx$$

3. $ϵ$-不敏感损失函数

SVR 使用 $ϵ$-不敏感损失函数，定义如下：

$$L_{ϵ}(y,f(x))=\{\begin{array}{ll}|y-f(x)|-ϵ,& \text{如果 }|y-f(x)|>ϵ\\ 0,& \text{否则}\end{array}$$

4. 拉格朗日函数

为了将问题转化为对偶问题，引入拉格朗日乘子 ${\alpha }_i$ 和 ${\alpha }_i^{\ast }$。拉格朗日函数 $L$ 表示为：

$$\begin{gathered} L(w,b,\xi ,{\xi }^{\ast },\alpha ,{\alpha }^{\ast })=\frac{1}{2}\Vert w{\Vert }^2 \\ +C\sum _{i=1}^m({\xi }_i+{\xi }_i^{\ast })-\sum _{i=1}^m{\alpha }_i(ϵ+{\xi }_i-y_i+⟨w,\varphi (x_i)⟩+b)-\sum _{i=1}^m{\alpha }_i^{\ast }(ϵ+{\xi }_i^{\ast }+y_i-⟨w,\varphi (x_i)⟩-b) \end{gathered}$$

5. 对偶问题

对 $w$ 和 $b$ 求偏导数并设为零，得到最优条件：

$$\frac{\partial L}{\partial w}=w-\sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })\varphi (x_i)=0\Rightarrow w=\sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })\varphi (x_i)$$

$$\frac{\partial L}{\partial b}=-\sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })=0\Rightarrow \sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })=0$$

将这些条件代入拉格朗日函数，得到对偶问题：

$$\underset{\alpha ,{\alpha }^{\ast }}{\max }\left(\sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })y_i-\frac{1}{2}\sum _{i,j=1}^m({\alpha }_i-{\alpha }_i^{\ast })({\alpha }_j-{\alpha }_j^{\ast })K(x_i,x_j)\right)$$

约束条件：

$$\sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })=0\text{和}0\le {\alpha }_i,{\alpha }_i^{\ast }\le C\forall i$$

其中 $K(x_i,x_j)=⟨\varphi (x_i),\varphi (x_j)⟩$ 是核函数。
为了使 SVR 能够处理非线性回归问题，通常使用核函数 $K({\mathbf{x}}_i,{\mathbf{x}}_j)$ 将输入数据映射到高维空间。常用的核函数包括：

• 线性核函数：$K({\mathbf{x}}_i,{\mathbf{x}}_j)={\mathbf{x}}_i^T{\mathbf{x}}_j$
• 多项式核函数：$K({\mathbf{x}}_i,{\mathbf{x}}_j)=(\gamma {\mathbf{x}}_i^T{\mathbf{x}}_j+r{)}^d$
• 高斯核（RBF）：$K({\mathbf{x}}_i,{\mathbf{x}}_j)=e^{-\gamma ||{\mathbf{x}}_i-{\mathbf{x}}_j|{|}^2}$

6. 解的重构

求解对偶问题后，得到 ${\alpha }_i$ 和 ${\alpha }_i^{\ast }$。利用这些值计算 $w$：

$$w=\sum _{i=1}^m({\alpha }_i-{\alpha }_i^{\ast })\varphi (x_i)$$

选择一个合适的样本 $j$，计算 $b$：

$$b=y_j-⟨w,\varphi (x_j)⟩$$
预测函数为：
$$f(x)=\sum _{i=1}^n({\alpha }_i-{\alpha }_i^{\ast })K(x_i,x)+b$$
其中 $b$ 通过支持向量计算得到。

7. 参数选择

• 正则化参数 $C$：控制模型复杂度和误差的平衡。较大的 $C$ 会使模型对误差更加敏感，可能导致过拟合；较小的 $C$ 可能导致欠拟合。
• $ϵ$ 容忍度：控制 $ϵ$-不敏感损失函数的阈值。较大的 $ϵ$ 会使模型对预测偏差更加宽容，而较小的 $ϵ$ 会使模型对误差更加敏感。
• 核函数：选择合适的核函数（如高斯核 $K(x,x^{\prime })=\exp (-\gamma \Vert x-x^{\prime }{\Vert }^2)$）可以捕捉数据中的复杂关系。

算法实现

手动实现

import numpy as np
from cvxopt import matrix, solvers
import matplotlib.pyplot as plt


class SVR:
    def __init__(self, C=1.0, epsilon=0.1):
        # 惩罚参数
        self.C = C
        # ε-不敏感损失函数的参数
        self.epsilon = epsilon
        # 权重向量
        self.w = None
        # 偏置项
        self.b = None

    def fit(self, X, y):
        n_samples, n_features = X.shape

        # 构建二次规划问题的参数
        # 目标函数中的二次项系数矩阵
        P = np.zeros((2 * n_samples, 2 * n_samples))
        for i in range(n_samples):
            for j in range(n_samples):
                P[i, j] = X[i].dot(X[j])
                P[i + n_samples, j + n_samples] = X[i].dot(X[j])
                P[i, j + n_samples] = -X[i].dot(X[j])
                P[i + n_samples, j] = -X[i].dot(X[j])
        P = matrix(P)

        # 目标函数中的一次项系数向量
        q = matrix(np.hstack([self.epsilon - y, self.epsilon + y]))

        # 不等式约束条件
        G1 = np.vstack([-np.eye(2 * n_samples), np.eye(2 * n_samples)])
        h1 = np.hstack([np.zeros(2 * n_samples), np.ones(2 * n_samples) * self.C])
        G = matrix(G1)
        h = matrix(h1)

        # 等式约束条件
        A = matrix(np.hstack([np.ones(n_samples), -np.ones(n_samples)]).reshape(1, -1))
        b = matrix(0.0)

        # 求解二次规划问题
        sol = solvers.qp(P, q, G, h, A, b)
        alphas = np.ravel(sol['x'])
        alphas_pos = alphas[:n_samples]
        alphas_neg = alphas[n_samples:]

        # 计算权重向量
        self.w = np.zeros(n_features)
        for i in range(n_samples):
            self.w += (alphas_pos[i] - alphas_neg[i]) * X[i]

        # 计算偏置项
        # 找到支持向量
        support_vectors = (alphas_pos > 1e-5) | (alphas_neg > 1e-5)
        self.b = 0
        for i in np.where(support_vectors)[0]:
            sgn = np.sign(alphas_pos[i] - alphas_neg[i])
            self.b += y[i] - sgn * self.epsilon - self.w.dot(X[i])
        self.b /= support_vectors.sum()

    def predict(self, X):
        return np.dot(X, self.w) + self.b


# 生成一些示例数据
np.random.seed(42)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.randn(80) * 0.1

# 创建SVR模型并拟合数据
svr = SVR(C=1.0, epsilon=0.1)
svr.fit(X, y)

# 生成用于绘制预测曲线的点
X_test = np.linspace(0, 5, 200)[:, np.newaxis]
y_pred = svr.predict(X_test)

# 绘制原始数据点
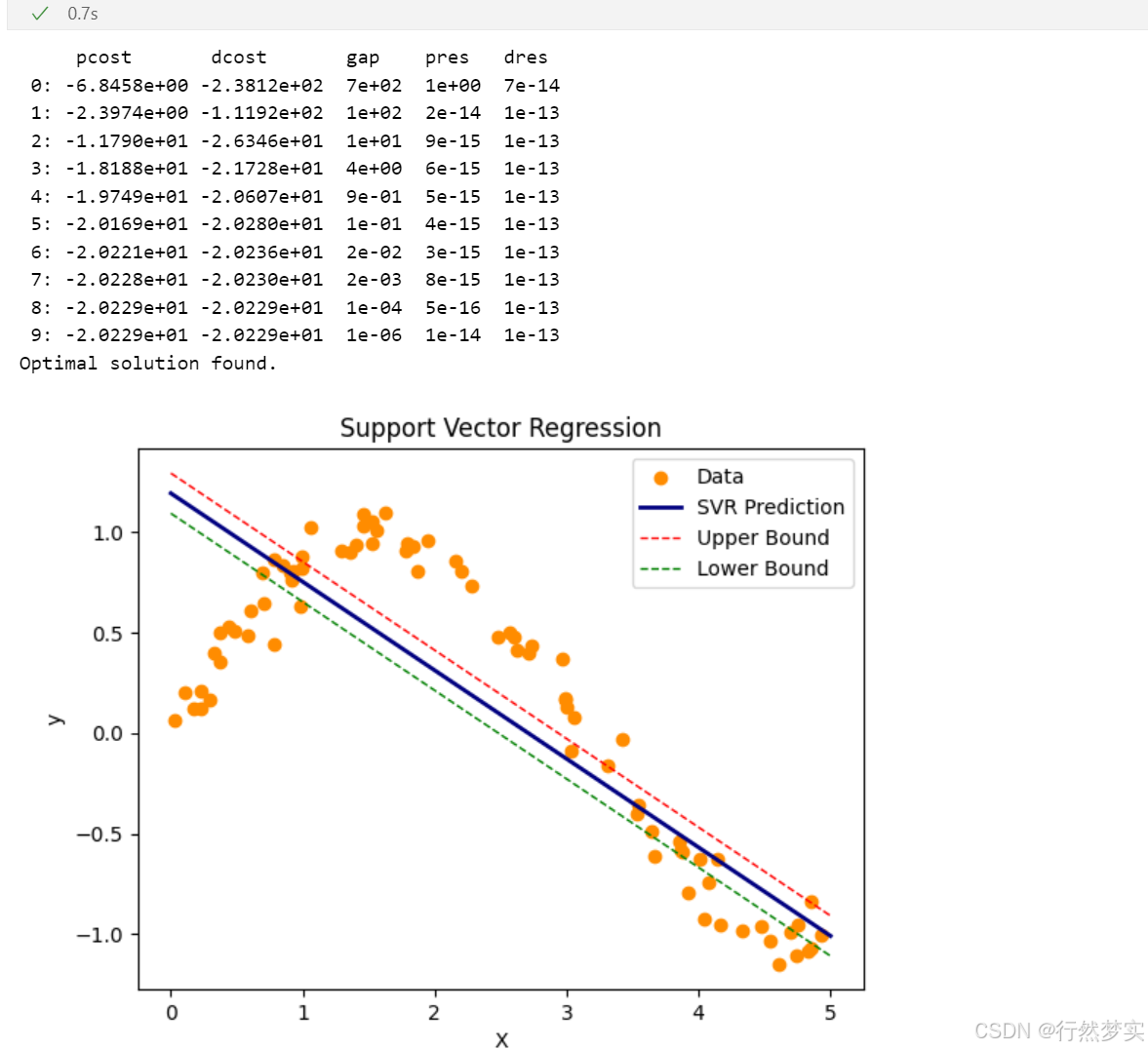
plt.scatter(X, y, color='darkorange', label='Data')
# 绘制预测曲线
plt.plot(X_test, y_pred, color='navy', lw=2, label='SVR Prediction')
# 绘制 ε-不敏感带
plt.plot(X_test, y_pred + svr.epsilon, color='red', lw=1, linestyle='--', label='Upper Bound')
plt.plot(X_test, y_pred - svr.epsilon, color='green', lw=1, linestyle='--', label='Lower Bound')

plt.xlabel('X')
plt.ylabel('y')
plt.title('Support Vector Regression')
plt.legend()
plt.show()

运行结果：

python函数库实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR

# 生成示例数据
np.random.seed(42)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.randn(80) * 0.1

# 创建不同核函数的SVR模型
svr_rbf = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=0.1)
svr_lin = SVR(kernel='linear', C=100, gamma='auto')
svr_poly = SVR(kernel='poly', C=100, gamma='auto', degree=3, epsilon=0.1, coef0=1)

# 训练模型
svr_rbf.fit(X, y)
svr_lin.fit(X, y)
svr_poly.fit(X, y)

# 生成用于预测的点
X_test = np.linspace(0, 5, 200)[:, np.newaxis]

# 进行预测
y_rbf = svr_rbf.predict(X_test)
y_lin = svr_lin.predict(X_test)
y_poly = svr_poly.predict(X_test)

# 可视化结果
plt.figure(figsize=(12, 8))
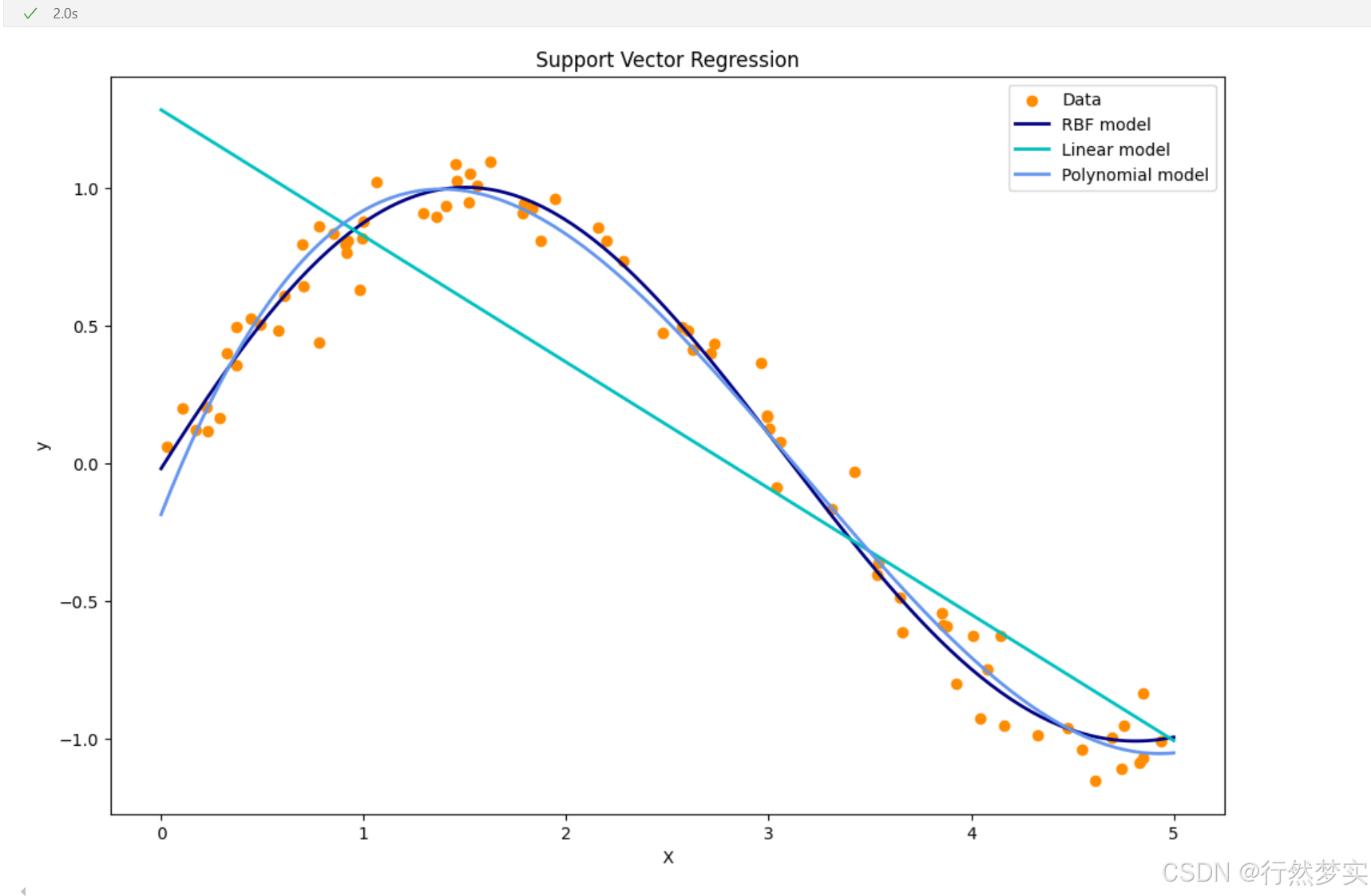
plt.scatter(X, y, color='darkorange', label='Data')
plt.plot(X_test, y_rbf, color='navy', lw=2, label='RBF model')
plt.plot(X_test, y_lin, color='c', lw=2, label='Linear model')
plt.plot(X_test, y_poly, color='cornflowerblue', lw=2, label='Polynomial model')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Support Vector Regression')
plt.legend()
plt.show()

运行结果：

在scikit-learn库中，svr_rbf.fit(X, y)、svr_lin.fit(X, y) 和 svr_poly.fit(X, y) 这三行代码分别用于训练使用径向基核（RBF）、线性核和多项式核的支持向量回归（SVR）模型。下面结合数学公式详细讲解其含义。

不同核函数下的具体含义

线性核（svr_lin.fit(X, y)）

当使用线性核时，$f(x)=w^{T}x+b$，优化问题就是在输入特征空间中寻找一个最优的超平面来拟合数据。在 fit 方法调用时，模型会求解上述优化问题以确定 $w$ 和 $b$ 的最优值。

在求解过程中，通常会将原问题转化为对偶问题：
$$\underset{\alpha ,{\alpha }^{\ast }}{\max }-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n({\alpha }_i-{\alpha }_i^{\ast })({\alpha }_j-{\alpha }_j^{\ast })x_i^T{x}_j-ϵ\sum _{i=1}^n({\alpha }_i+{\alpha }_i^{\ast })+\sum _{i=1}^n{y}_i({\alpha }_i-{\alpha }_i^{\ast })$$
$$\text{s.t.}\{\begin{array}{l}{\sum }_{i=1}^n({\alpha }_i-{\alpha }_i^{\ast })=0\\ 0\le {\alpha }_i,{\alpha }_i^{\ast }\le C\end{array}$$
其中 ${\alpha }_i$ 和 ${\alpha }_i^{\ast }$ 是拉格朗日乘子。求解对偶问题得到最优的拉格朗日乘子后，就可以计算出 $w={\sum }_{i=1}^n({\alpha }_i-{\alpha }_i^{\ast })x_i$，再通过满足 Karush - Kuhn - Tucker（KKT）条件的样本计算出 $b$。

径向基核（RBF）（svr_rbf.fit(X, y)）

径向基核函数的表达式为 $K(x_i,x_j)=\exp (-\gamma \Vert x_i-x_j{\Vert }^2)$，其中 $\gamma$ 是核系数。

在使用径向基核时，模型会将输入数据映射到一个高维特征空间，在这个高维空间中进行线性回归。对偶问题变为：
$$\underset{\alpha ,{\alpha }^{\ast }}{\max }-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n({\alpha }_i-{\alpha }_i^{\ast })({\alpha }_j-{\alpha }_j^{\ast })K(x_i,x_j)-ϵ\sum _{i=1}^n({\alpha }_i+{\alpha }_i^{\ast })+\sum _{i=1}^n{y}_i({\alpha }_i-{\alpha }_i^{\ast })$$
$$\text{s.t.}\{\begin{array}{l}{\sum }_{i=1}^n({\alpha }_i-{\alpha }_i^{\ast })=0\\ 0\le {\alpha }_i,{\alpha }_i^{\ast }\le C\end{array}$$
svr_rbf.fit(X, y) 会求解上述对偶问题，得到最优的拉格朗日乘子，然后在预测时使用 $f(x)={\sum }_{i=1}^n({\alpha }_i-{\alpha }_i^{\ast })K(x_i,x)+b$ 进行预测。

多项式核（svr_poly.fit(X, y)）

多项式核函数的表达式为 $K(x_i,x_j)=(\gamma x_i^T{x}_j+r{)}^d$，其中 $\gamma$ 是核系数，$r$ 是偏置项，$d$ 是多项式的次数。

同样，在使用多项式核时，模型会将输入数据映射到高维特征空间并求解对偶问题：
$$\underset{\alpha ,{\alpha }^{\ast }}{\max }-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n({\alpha }_i-{\alpha }_i^{\ast })({\alpha }_j-{\alpha }_j^{\ast })K(x_i,x_j)-ϵ\sum _{i=1}^n({\alpha }_i+{\alpha }_i^{\ast })+\sum _{i=1}^n{y}_i({\alpha }_i-{\alpha }_i^{\ast })$$
$$\text{s.t.}\{\begin{array}{l}{\sum }_{i=1}^n({\alpha }_i-{\alpha }_i^{\ast })=0\\ 0\le {\alpha }_i,{\alpha }_i^{\ast }\le C\end{array}$$
svr_poly.fit(X, y) 会根据输入的训练数据 $X$ 和目标值 $y$ 求解这个对偶问题，确定最优的拉格朗日乘子，进而得到用于预测的函数 $f(x)={\sum }_{i=1}^n({\alpha }_i-{\alpha }_i^{\ast })K(x_i,x)+b$。

fit 方法的本质是根据不同的核函数，求解对应的优化问题，以确定模型的参数，从而使得模型能够对输入数据进行有效的拟合和预测。