Ref:
https://www.zhihu.com/question/56024942
http://m.blog.csdn.net/chaipp0607/article/details/60868689
1*1卷积的主要作用有以下几点:
1、降维( dimension reductionality )。比如,一张500 * 500且厚度depth为100 的图片在20个filter上做1*1的卷积,那么结果的大小为500*500*20。
2、加入非线性。卷积层之后经过激励层,1*1的卷积在前一层的学习表示上添加了非线性激励( non-linear activation ),提升网络的表达能力;
当1*1卷积出现时,在大多数情况下它作用是升/降特征的维度,这里的维度指的是通道数(厚度),而不改变图片的宽和高。
举个例子,比如某次卷积之后的结果是W*H*6的特征,现在需要用1*1的卷积核将其降维成W*H*5,即6个通道变成5个通道:
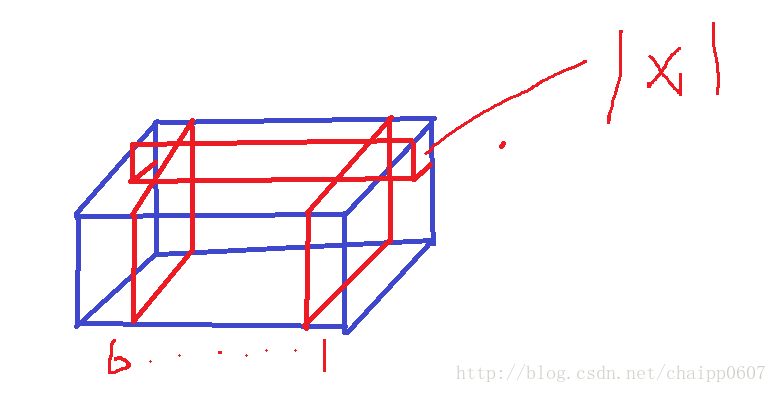
如下图就是一个W*H*6的特征,而1*1的卷积核在图上标出,卷积核自身的厚度也是6(图画的好难看!!)
通过一次卷积操作,W*H*6将变为W*H*1,这样的话,使用5个1*1的卷积核,显然可以卷积出5个W*H*1,再做通道的串接操作,就实现了W*H*5。
在这里先计算一下参数数量,一遍后面说明,5个卷积核,每个卷积核的尺寸是1*1*6,也就是一种有30个参数。
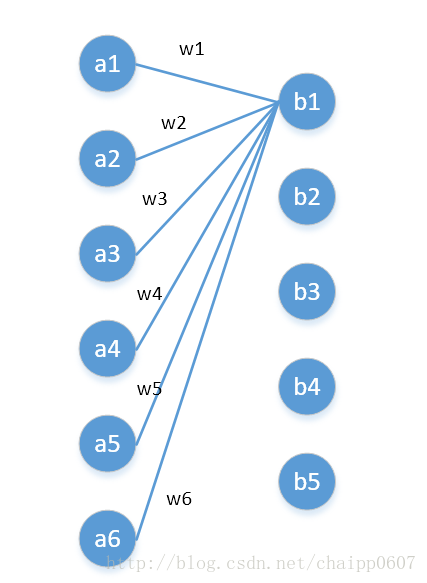
我们还可以用另一种角度去理解1*1卷积,可以把它看成是一种全连接,如下图:
第一层有6个神经元,分别是a1—a6,通过全连接之后变成5个,分别是b1—b5,第一层的六个神经元要和后面五个实现全连接,本图中只画了a1—a6连接到b1的示意,可以看到,在全连接层b1其实是前面6个神经元的加权和,权对应的就是w1—w6,到这里就很清晰了:
第一层的6个神经元其实就相当于输入特征里面那个通道数:6,而第二层的5个神经元相当于1*1卷积之后的新的特征通道数:5。
w1—w6是一个卷积核的权系数,如何要计算b2—b5,显然还需要4个同样尺寸的核。
最后一个问题,图像的一层相比于神经元还是有区别的,这在于是一个2D矩阵还是一个数字,但是即便是一个2D矩阵的话也还是只需要一个参数(1*1的核),这就是因为参数的权值共享。