题目列表
3417. 跳过交替单元格的之字形遍历
3418. 机器人可以获得的最大金币数
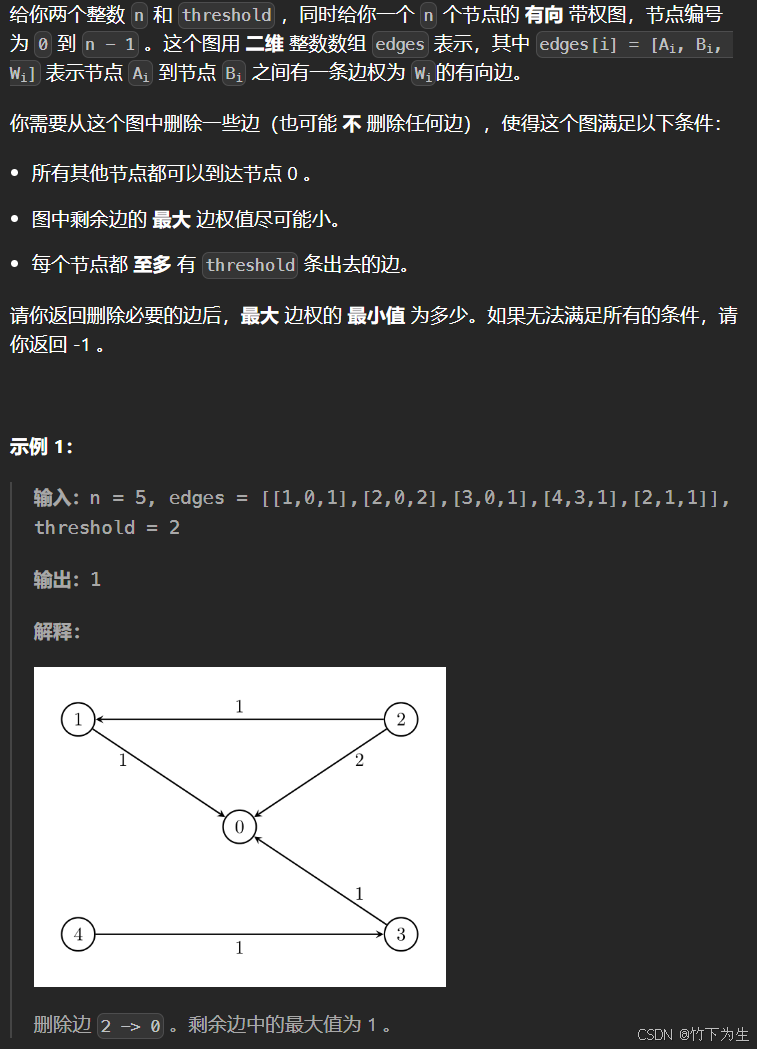
3419. 图的最大边权的最小值
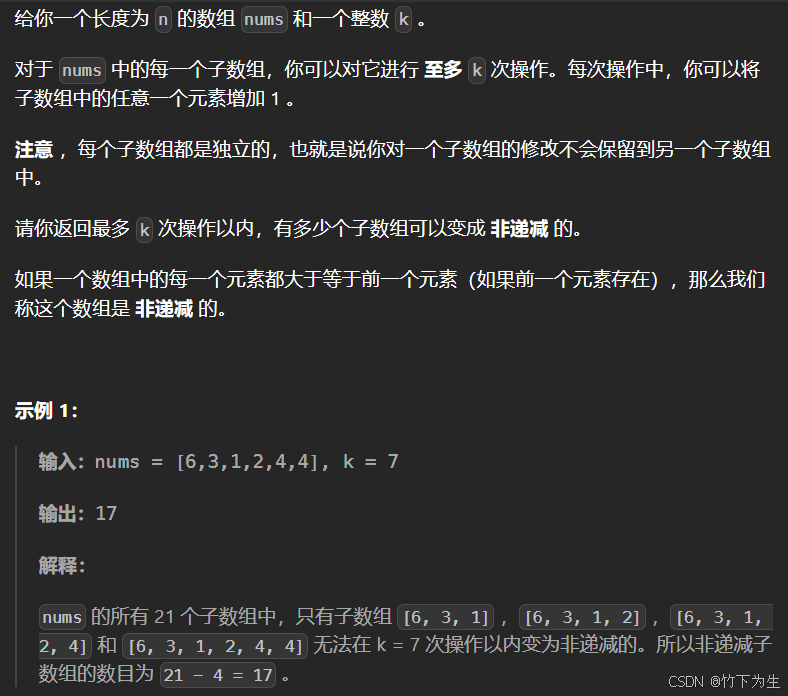
3420. 统计 K 次操作以内得到非递减子数组的数目
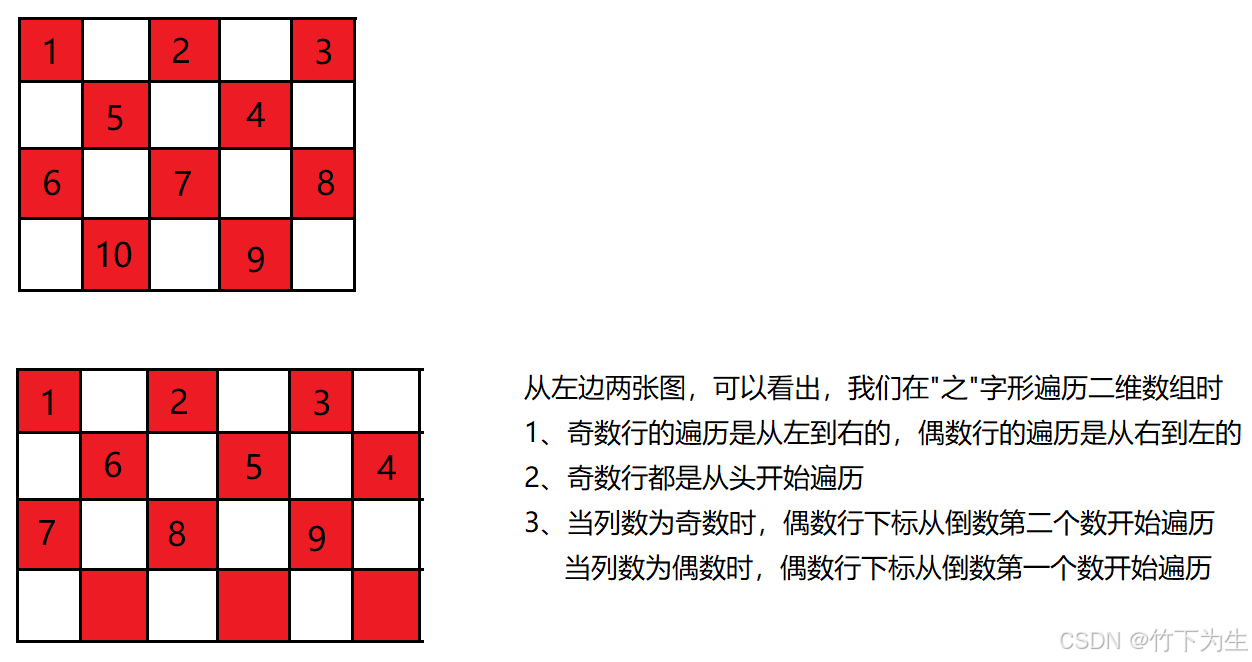
一、跳过交替单元格的之字形遍历
题目要求 “之” 字形遍历数组,具体规律如下
具体代码如下
class Solution {
public:
vector<int> zigzagTraversal(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<int> res;
for(int i = 0; i < n; i++){
if(i % 2 == 0){ // 奇数行,从前往后遍历
for(int j = 0; j < m; j += 2){
res.push_back(grid[i][j]);
}
}else{ // 偶数行,从后往前遍历
for(int j = m - 1 - m % 2; j >= 0; j -= 2){
res.push_back(grid[i][j]);
}
}
}
return res;
}
};
// 也可以将偶数行的进行逆序
class Solution {
public:
vector<int> zigzagTraversal(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<int> res;
bool ok = true;
for(int i = 0; i < n; i++){
if(i % 2)
reverse(grid[i].begin(), grid[i].end());
for(auto x : grid[i]){
if(ok)
res.push_back(x);
ok = !ok;
}
}
return res;
}
};
二、机器人可以获得的最大金币数
经典的走格子
d
p
dp
dp 问题。我们还是先确定状态定义,除了需要知道当前格子下标
(
i
,
j
)
(i, j)
(i,j),还需要额外知道当前用了几次感化能力,从而来判断是否还能使用感化能力。
- 状态定义: f [ i ] [ j ] [ k ] f[i][j][k] f[i][j][k] 表示使用了 k k k 次感化能力到达 ( i , j ) (i, j) (i,j) 时的最大金币数
- 状态转移方程:
- 当不使用感化能力时,直接从 ( i , j − 1 ) (i,j-1) (i,j−1) 和 ( i , j − 1 ) (i,j-1) (i,j−1) 转移过来, f [ i ] [ j ] [ k ] = m a x ( f [ i − 1 ] [ j ] [ k ] , f [ i ] [ j − 1 ] [ k ] ) + c o i n s [ i ] [ j ] f[i][j][k]=max(f[i-1][j][k],f[i][j-1][k])+coins[i][j] f[i][j][k]=max(f[i−1][j][k],f[i][j−1][k])+coins[i][j]
- 当使用感化能力时(此时 c o i n s [ i ] [ j ] < 0 coins[i][j]<0 coins[i][j]<0),同时确保 k > 0 k>0 k>0,此时 f [ i ] [ j ] [ k ] = m a x ( f [ i − 1 ] [ j ] [ k − 1 ] , f [ i ] [ j − 1 ] [ k − 1 ] ) f[i][j][k]=max(f[i-1][j][k-1],f[i][j-1][k-1]) f[i][j][k]=max(f[i−1][j][k−1],f[i][j−1][k−1]),由于使用了感化能力,所以 ( i , j − 1 ) (i,j-1) (i,j−1) 和 ( i , j − 1 ) (i,j-1) (i,j−1) 状态的 k k k 需要减一
- 注意:由于我们不清楚什么时候需要使用感化能力,所以每一个格子,我们都需要计算出使用感化能力和不使用感化能力的金币数,取较大值
- 状态初始化:
- 为了方便状态转移,我们将 f f f 数组的前两个维度大小都 + 1 +1 +1,这样原本 ( x , y ) (x,y) (x,y) 位置的状态等价变成了 ( x + 1 , y + 1 ) (x+1,y+1) (x+1,y+1) 的状态,原本第一行和第一列的状态转移的越界问题就被解决了,此时我们只要将多出的这些状态进行初始化即可。
- 由于本题的答案可以为负数,为了不影响取 m a x max max 后的状态结果,我们将所有位置的值初始化为 − ∞ -\infty −∞,需要注意的是 f [ 1 ] [ 1 ] [ k ] f[1][1][k] f[1][1][k] 这个初始状态表示 ( 0 , 0 ) (0,0) (0,0) 位置状态的值,它不能由任何状态转移而来,只能由它自己决定,为了保证状态转移的正确性,我们需要将 f [ 0 ] [ 1 ] [ k ] f[0][1][k] f[0][1][k] 或者 f [ 0 ] [ 1 ] [ k ] f[0][1][k] f[0][1][k] 初始化为 0 0 0
具体代码如下
class Solution {
public:
int maximumAmount(vector<vector<int>>& coins) {
int n = coins.size(), m = coins[0].size();
// 由于答案可能为负数,所以不能初始化为0,需要初始化为无穷小,这样不会妨碍取 max
// 注意:这里的"无穷小"只要是一个比可能的最小答案还要小的值即可
vector f(n + 1, vector<vector<int>>(m + 1, vector<int>(3, INT_MIN/2)));
f[0][1] = vector<int>(3);
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
for(int k = 0; k < 3; k++){
f[i+1][j+1][k] = max(f[i][j+1][k], f[i+1][j][k]) + coins[i][j];
if(k && coins[i][j] < 0){ // 记得和没有使用感化能力获得的金币数取max
f[i+1][j+1][k] = max({f[i+1][j+1][k], f[i][j+1][k-1], f[i+1][j][k-1]});
}
}
}
}
return f.back().back().back();
}
};
三、图的最大边权的最小值
看到最大最小,就要想到二分答案,这题同样可以二分,因为最大边权越大,可选择的边越多,越可能否和题目条件。关键在于如何写
c
h
e
c
k
check
check 函数,即如何判断最大边权为
k
k
k 时,答案是否满足条件
- 所有结点都能到达 0 0 0 节点,反过来即 0 0 0 节点能达到任何一个结点,我们只要建立一个反图,然后从 0 0 0 节点开始 d f s dfs dfs 遍历,看是否能到达所有的结点即可
- 每个节点最多有 t h r e s h o l d threshold threshold 条边,这个条件其实就包含在 d f s dfs dfs 遍历之中,想想遍历的具体流程,我们会给遍历过的结点打上标记,不会重复遍历,也就是说只会有一个结点能到达当前结点,由于我们建立的是返图,所以当前节点只有一条边指向其他节点,而 t h r e s h o l d ⩾ 1 threshold\geqslant1 threshold⩾1,所以该条件一定满足
代码如下
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int,int>>> g(n);
int mn = INT_MAX, mx = INT_MIN;
for(auto e: edges){
g[e[1]].emplace_back(e[0], e[2]);
mn = min(e[2], mn);
mx = max(e[2], mx);
}
// 判断是否从零可以到达所有结点
vector<int> vis(n); // 这里将遍历到的节点的 vis[i] 置为 k,这样不需要每次 dfs 都去初始化 vis 数组
auto check = [&](int k)->bool{
int cnt = 0;
auto dfs = [&](this auto&& dfs, int x)->void{
vis[x] = k;
cnt++;
for(auto [y, w]:g[x]){
if(vis[y] == k || w > k) continue;
dfs(y);
}
};
dfs(0);
return cnt == n;
};
int l = mn, r = mx;
while(l <= r){
int mid = l + (r - l)/2;
if(check(mid)) r = mid - 1;
else l = mid + 1;
}
if(l > mx) return -1;
return l;
}
};
四、统计 K 次操作以内得到非递减子数组的数目
题目要求合法子数组的个数,且子数组需要满足在
k
k
k 次操作以内,使得子数组可以变成非递减的,每次操作可以将数
+
1
+1
+1。
显而易见,子数组越大,需要进行的操作越多,就越难满足题目要求,具有单调性,可以用滑动窗口来写,维护以
r
r
r 为右端点的窗口内的最大合法子数组,故以
r
r
r 为右端点的合法子数组的个数为
r
−
l
+
1
r-l+1
r−l+1
- 进窗口:操作数加上
m
a
x
(
当前窗口的最大值
−
n
u
m
s
[
r
]
,
0
)
max(当前窗口的最大值-nums[r], 0)
max(当前窗口的最大值−nums[r],0)
- 如何维护区间最大值?用单调队列,队列中存放下标。
- 当 [ l , r ] [l,r] [l,r] 区间的 r + 1 r+1 r+1 后,队列中只要是 ⩽ n u m s [ r ] \leqslant nums[r] ⩽nums[r] 的数的下标都需要被 p o p _ b a c k pop\_back pop_back,因为它们永远无法成为区间的最大值了,然后 p u s h _ b a c k ( r ) push\_back(r) push_back(r)
- 当 [ l , r ] [l,r] [l,r] 区间的 l + 1 l+1 l+1 后,队列中只要是 < l < l <l 的数,都需要被 p o p _ f r o n t pop\_front pop_front,因为它们不在区间中了
- 区间 [ l , r ] [l,r] [l,r] 中的最大值为 n u m s [ q . f r o n t ( ) ] nums[q.front()] nums[q.front()]
- 如何维护区间最大值?用单调队列,队列中存放下标。
- 出窗口:当操作总次数
s
u
m
>
k
sum>k
sum>k 时,我们需要移动左端点
l
l
l,此时,我们需要减去由
n
u
m
s
[
l
]
nums[l]
nums[l] 引发的操作数。具体情况如下图
代码如下
class Solution {
public:
long long countNonDecreasingSubarrays(vector<int>& nums, int k) {
int n = nums.size();
stack<int> st;
vector<int> right(n, n); // 记录离 i 最近的右边的大于 nums[i] 的第一个数下标
vector<vector<int>> g(n); // g[l] 中记录 nums[l] 能影响的操作数的关键数字下标,即上图中的 5、6、7 这些数字的下标
for(int i = 0; i < n; i++){
while(st.size() && nums[st.top()] < nums[i]){
right[st.top()] = i;
st.pop();
}
if(st.size()){
g[st.top()].push_back(i);
}
st.push(i);
}
deque<int> dq; // 单调队列
long long ans = 0, sum = 0;
for(int l = 0, r = 0; r < n; r++){ // 滑动窗口
while(dq.size() && nums[dq.back()] <= nums[r]){
dq.pop_back();
}
dq.push_back(r);
sum += max(nums[dq.front()] - nums[r], 0); // 进窗口
while(sum > k){ // 出窗口
int out = nums[l];
for(int i: g[l]){ // 减去 nums[l] 对当前窗口的操作数的影响
if(i > r) break;
sum -= 1LL*(out - nums[i])*(min(right[i], r + 1) - i);
}
l++;
}
ans += r - l + 1;
while(dq.size() && dq.front() < l)
dq.pop_front();
}
return ans;
}
};