🌟快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。 🌟
别再犹豫了!快来订阅我们的算法每日双题精讲专栏,一起踏上算法学习的精彩之旅吧💪
在算法的浩瀚星空中✨,二分查找算法宛如一颗璀璨的明星🌟,闪耀着简洁与高效的光芒。今天,就让我们一同聚焦于 “x的平方根” 以及 “搜索插入位置” 这两道经典题目,深度挖掘二分查找算法的奥秘与应用技巧🤓。
不要跳过每一个二分查找算法文章哦,难度逐渐提升 !
目录
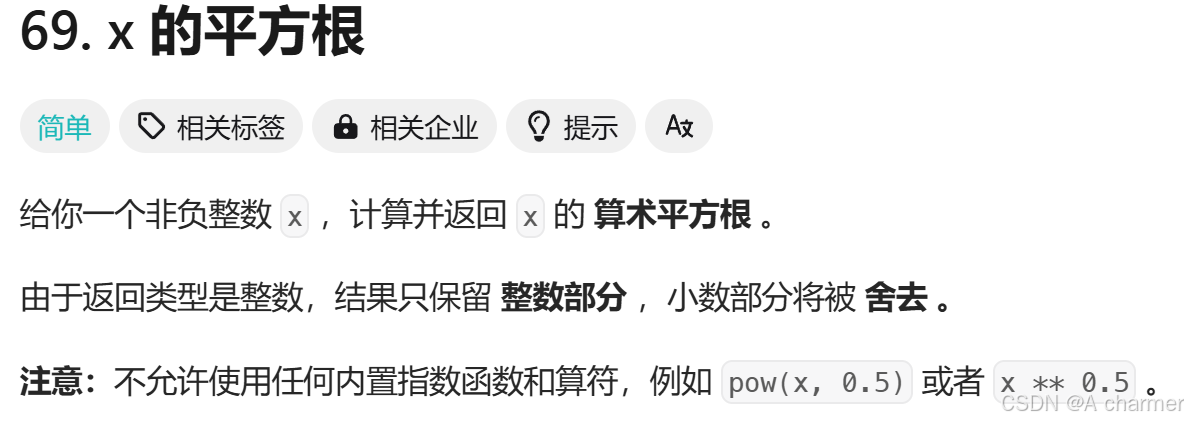
一、x 的平方根
题目链接👉【力扣】
📖题目描述
🧠讲解算法原理
这里我们巧妙地运用二分查找来解决问题。
首先,设定左边界
left为0,右边界right为x。在循环过程中,计算中间值mid = left + (right - left) / 2(这种计算方式能有效避免整数溢出哦😉)。接着,比较
mid的平方与x的大小关系:若mid * mid == x,那么mid就是我们苦苦寻觅的x的平方根;若mid * mid < x,这意味着x的平方根在mid的右侧,我们就将left更新为mid + 1;若mid * mid > x,则表明x的平方根在mid的左侧,此时将right更新为mid - 1。循环持续进行,直到
left大于right,此时right就是x的平方根向下取整的结果啦。
💻代码实现(以 C++ 为例)
class Solution {
public:
int mySqrt(int x) {
if (x < 1) return 0;
int left = 1, right = x;
while (left < right)
{
long long mid = left + (right - left) / 2;
if (mid * mid <= x)
{
left = mid;
}
else
right = mid - 1;
}
return left;
}
};复杂度分析
- 时间复杂度:由于每次循环都能将搜索区间缩小一半,所以时间复杂度为
,相较于从
0到x逐个尝试的暴力解法(时间复杂度为),速度有了极大的提升。
- 空间复杂度:整个过程只需要几个额外的变量来记录边界和中间值,无需额外的复杂数据结构,空间复杂度为
,非常节省空间。
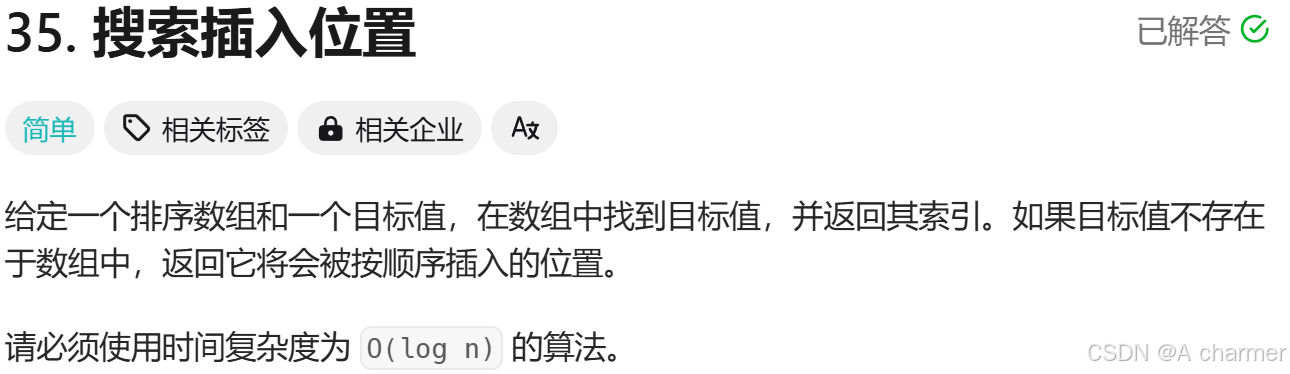
二、搜索插入位置
题目链接👉【力扣】
📖题目描述
🧠讲解算法原理
同样借助二分查找的强大力量。先初始化左指针
left为0,右指针right为数组长度减1。在循环中,计算中间索引mid = left + (right - left) / 2。若nums[mid] == target,直接返回mid即可;若nums[mid] < target,说明目标值在mid的右侧,将left更新为mid + 1;若nums[mid] > target,表明目标值在mid的左侧,将right更新为mid - 1。当循环结束(即left > right)时,left就是目标值应该插入的位置索引。
💻代码实现(以 C++ 为例)
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int right=nums.size()-1,left=0;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]<target)
{
left=mid+1;
}
else if(nums[mid]>=target)
{
right=mid;
}
}
if(nums[left]<target)
return left+1;
return left;
}
};复杂度分析
- 时间复杂度:每次循环搜索区间减半,时间复杂度为
,其中
n为数组nums的长度,能高效地在有序数组中定位目标或插入位置。- 空间复杂度:仅需少量额外变量存储指针和中间索引,空间复杂度为
,在空间利用上表现出色。
通过对这两道题目的详细解析,我们更加深刻地领略了二分查找算法的魅力与实用性。在今后的算法学习旅程中,一定要牢牢掌握二分查找及其各种变形应用,让我们在解决问题的道路上更加得心应手。继续加油哦!💪
我将持续在算法领域精研深耕,为大家带来更多优质的算法知识讲解与问题剖析。
欢迎大家关注我 👉【A charmer】