题目链接

翻转对

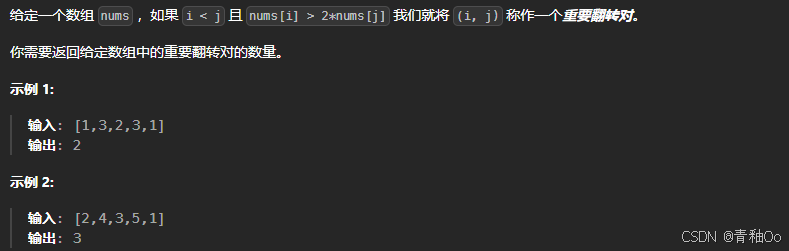
题目描述

注意点

• 给定数组的长度不会超过50000
• 输入数组中的所有数字都在32位整数的表示范围内

解答思路

• 本题与区间和的个数类似，都是使用归并排序统计满足题意的数量，归并排序后可以有效减少比较的数量
• 归并排序的思路为：将数组一分为二后，对两个数组各自按升序排序，随后i从数组1左侧开始，确定i后j从数组2左侧开始，找到第一个不满足nums[i] > nums[j] * 2的位置，本次i位置的数字的翻转对数量就是j - mid - 1。移动i重复上述过程，需要注意的是随着i从左往右移动，i对应的数字逐渐增大，数组2中之前满足翻转对的位置在下一次遍历时肯定也满足翻转对，所以j只需要一直向右移动

代码

class Solution {
    public int reversePairs(int[] nums) {
        return mergeSortCount(nums, 0, nums.length - 1);
    }

    public int mergeSortCount(int[] nums, int left, int right) {
        if (left >= right) {
            return 0;
        }
        int res = 0;
        int mid = left + ((right - left) >> 1);
        res += mergeSortCount(nums, left, mid);
        res += mergeSortCount(nums, mid + 1, right);
        int j = mid + 1;
        for (int i = left; i <= mid; i++) {
            while (j <= right && (long) nums[i] > (long) nums[j] * 2) {
                j++;
            }
            res += j - mid - 1;
        }
        // 归并排序
        int[] newArr = mergeSort(nums, left, right, mid);
        for (int i = 0; i < newArr.length; i++) {
            nums[left + i] = newArr[i];
        }
        return res;
    }

    public int[] mergeSort(int[] nums, int left, int right, int mid) {
        int[] newArr = new int[right - left + 1];
        int i = left, j = mid + 1, idx = 0;
        while (i <= mid || j <= right) {
            if (i > mid) {
                newArr[idx++] = nums[j++];
                continue;
            }
            if (j > right) {
                newArr[idx++] = nums[i++];
                continue;
            }
            if (nums[i] > nums[j]) {
                newArr[idx++] = nums[j++];
            } else {
                newArr[idx++] = nums[i++];
            }
        }
        return newArr;
    }
}

关键点

• 归并排序的思想
• 输入数组中的所有数字都在32位整数的表示范围内，乘以2后可能会发生越界，所以需要转为long比较大小