CNN—LeNet：从0开始神经网络学习，实战MNIST和CIFAR10~

前言

作为入门神经网络的小白，对CNN和LeNet在学习后的一些感悟，本教程比较通俗易懂，对数学原理及其代码进行讲解，主要从LeNet的架构，整体运行的相关名词与框架进行了解释。这是属于深度学习的新手村，并打俩新手村boss，MNIST和CIFAR10
文章比较长，可以根据感兴趣的部分跳转到对应位置，希望能对你的学习有所帮助哦

一、CNN与LeNet介绍

这里对比介绍一下概念叭
CNN：神经网络类别，用于视觉任务，一类卷积神经网络
LeNet：具体的第一个CNN架构，结构简单，适合神经网络的入门

所以记得大佬说CNN的时候通常指视觉神经网络。LeNet通常用于入门，结构简单，后面就基本不用该模型了嘞

二、LeNet组成及其名词解释

一个标准的LeNet-5其实由以下7层组成

层数	名称	介绍
C1、C3	卷积层	使用卷积核对输入进行卷积，得到具有更高通道以及想要大小的输出
C2、C4	池化层	分为最大池化与平均池化，获得指定区域中的最大值或者平均值。
C5、C6、C7	全连接层	将张量展平，

2.1 输入

对输入的数据有充分的了解，是构建任何一个模型的前提
本次主要采用两个数据集，入门的MNIST手写字体灰色图识别(-1, 1, 28, 28)和CIFAR10物体彩色图（三通道rgb）识别(-1, 3, 32, 32)

2.2 卷积层

卷积层，那么它的作用就是把输入卷起来，那它要卷输入的什么，以及用什么进行卷积呢？
卷积核就是卷积层的核心之一，也被称为滤波器，一般选择3x3，5x5，而1x1的卷积核通常用于增加通道数
在这里插入图片描述

图中7x7是输入的矩阵，图中颜色的3x3部分对应了一个卷积核的大小。
卷积核会成为滚动窗口遍历所有位置，从代码角度来看就是卷积核会从左上方不断像右一行一行的遍历过去，并将遍历的值放入输出层对应的位置（如红绿蓝）。
遍历的过程中，涉及的计算为点积。 $X\cdot K$ ，K为卷积核。也就是将卷积核与输入的对应区域中，每一个对应位置相乘的值进行求和。
于是乎，我们可以利用代码写出一个基本的卷积层
事实上，由于卷积核中心与边缘有差距，所以在卷积的过程中可能会导致边缘数据的缺失，这时候就需要补零层
顾名思义补零层就是在输入的最外层额外补充想要圈数的0
那么对于下一层的输入，也就是卷积层的输出，其公式为
$S_o = \frac{S_i - K + 2P}{step} + 1$
$S_o$ 是输出层的大小， $S_{i}$ 是输入层的大小，K是内核大小，P是补零层大小（因为上下左右都会补0所以padding1其实长宽会增加2），step是步长，通常取1。加一的实质可以看成数人头时要记得把自己算进去

def conv(input_floor, kernel, padding=0):
    if padding != 0:
    	input_floor = np.pad(input_floor, (pading, pading), "constant")  # 参数解析：想要拓展的矩阵，拓展大小（行，列），拓展方式
    kernel_h, kernel_w = kernel.shape  # 获得内核大小
    input_h, input_w = input_floor.shape  # 获得输入大小
    output_h, output_w = kernel_h - input_h + 1, kernel_w - input_w + 1  # 获得输出大小
    # 初始化out_put
    output = np.zeros(output_h, output_w)
    # 接下来通过滚动窗口的方法，取出与卷积核相同大小的矩阵块
    for i in range(output_h):
        for j in range(output_w):
            reflect = input_floor[i: i + input_h, j: j + input_w]  # 取出当前输入的滚动窗口
            output[i, j] = np.sum(reflect * kernel)  # 进行numpy中的点积运算
    return output

小提示：

卷积核层面：上面讲的内容都是1x3x3的卷积核，不过实际运用中通常卷积核层数都不为一，输出的通道数只与卷积核的层数有关哦~ 例如一个(2, 3, 3)的卷积核与任给一个输入，输出的通道数都为2
输入层面：上面讲的内容是单通道下的输入，不过大部分时候我们需要处理彩色图像，也就是三通道的rgb图像，那么此时的卷积就需要结合多通道进行，将三个通道分别进行卷积，并将卷积的结果进行求和

2.3池化层

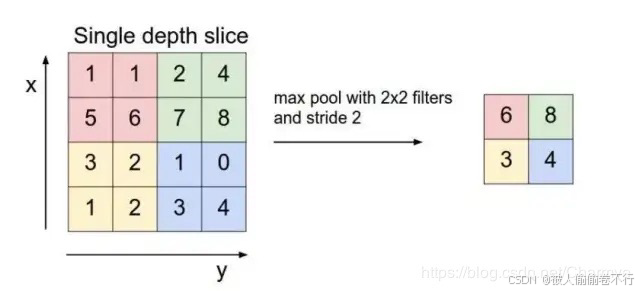
池化是一个名词，听起来莫名奇怪的，其实和卷积层相类似，利用滚动窗口，取出一个区间的最大值或平均值 在这里插入图片描述
池化分为最大池化和平均池化，如图中则为最大池化
红色区域的最大值为6，绿色区域的最大值为8……
为什么要池化呢？我们可以发现，经过池化之后的数据明显变小了，从原来的4x4降到了2x2，这就是池化的目的——在尽量维持数据精度的情况下压缩数据，好处可以是帮助快速收敛，防止过拟合
对于池化的选择：
最大池化：提取局部区域的最大值，突出显著特征。
平均池化：计算局部区域的平均值，更适合平滑特征图
注意：步频通常与核的大小一致，使得区域不重叠
所以通常池化后的输出大小为： $\frac{S_{0}} { K}$ ,长宽同时缩小K倍

def pool(input_floor, step, kernel_type="max"):
    """输入输出层与类型，分为max pool和mean pool，进行压缩, 要求池化后的大小是输入层的因子之一"""
    input_h, input_w = input_floor.shape
    if input_h % step != 0 or  input_w % step != 0:
        raise ValueError("Can't catch the size between input and output")
    output = np.zeros(input_h // step, input_w // step)
    for i in range(0, input_h // step):
        for j in range(0, input_w // step):
            reflect = input_floor[i * step: (i + 1) * step, j * step: (j + 1) * step]  # 取出核对应区域
            if kernel_type == "mean":
                output[i, j] = np.mean(reflect)
            else:
                output[i, j] = np.max(reflect)
    return output

2.4 全连接层

首先需要将所有的通道展开，使用nn.flatten()
在LeNet中将会通过C5、C6、C7三个全连接层，将展开的向量进行特征整合，逐步降低大小，最后一层输出结果
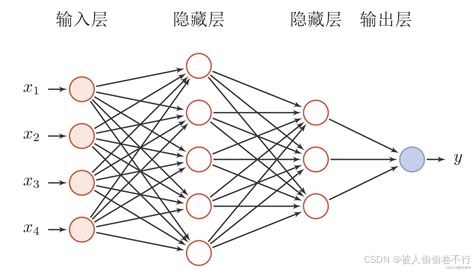
例如：(-1, 4, 1, 1)的4通道1长1宽的tensor，经过flatten后向量的长度为 $4 * 1 * 1 = 4$ ，我们可以自定义全连接层中的神经元数量，以此改变输出结果：
4 ->5->3->1（设定不同的神经元数量会影响中间过程，进而影响到结果，这里上网找了一张例图方便理解）
在这里插入图片描述
常见的激活函数，在LeNet中，过去使用Sigmoid，现在直接使用非线性的ReLU即可
$L in e a r (x) = W * x + b$
$R e l u (x) = M a x (0, x)$
$\frac{1}{1+e^{-x}}$
$\frac{e^{-x}}{\Sigma_{i} e^{-x_i}}$
$\frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$

2.5 总结

了解LeNet中几个层的重点，我们可以开始代码实战。不过依据数学原理造的”轮子“泛用性不强，关键点在于帮助我们理解卷积层与池化层，在实际应用中仍然还是以pytorch或tensorflow为主

三、MNIST实战

在开始敲代码前，再强调一定要先对数据集有个基本认识
MNIST数据集中，手写字体灰色图识别(-1, 1, 28, 28)
敲一个神经网络的模板

3.1 构建神经网络

模板套用即可

定义类继承于父类nn.Module
super().init()
self.model = nn.Sequential(填入神经网络的结构，LeNet一共填入7层，并且在每一次卷积与线性变换之后，都需要进行激活)
定义forward(self, x)函数，前向传播，固定return self.model(x)

小贴士：强烈推荐在写结构的时候每一层都标注出输入或输出的尺寸，可以帮助你更好的进行输入
并且通过model_layer函数能够打印每一层的尺寸，更加直观的看到神经网络中的运行

class LeNet(nn.Module):
    def __init__(self) -> None:
        super().__init__()
        self.model = nn.Sequential(
            # C1卷积，(-1, 1, 28, 28)
            # 输入的图片尺寸为1, 28, 28,一通道长28宽28的灰度图片，卷积核5×5
            # 几个参数的含义：
            # in_channels输入的通道数，out对应输出的通道数，kernel_size代表卷积核，stride代表步长为1，padding代表了补零层的大小，向外扩张两个0
            # 尺寸公式的计算: (length - kernel_size + 1 + 2 * padding) / stride
            # 用中文解释就是，长度-内核尺寸 + 1（类似于算入自己的意思） + 2 * 补零层(会影响下一层尺寸) / 步长
            nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=2),
            # 激活函数
            nn.Sigmoid(),
            # C2最大池化 (-1, 6, 14, 14)
            # 池化的目的在于压缩数据量，保留特征的同时方便处理，并且减少过拟合风险
            nn.MaxPool2d(kernel_size=2, stride=2), # 进行最大池化，2x2的面积，所以最后为(-1, 6, 14, 14)长宽各缩短一半，
            # C3卷积 (-1, 16, 10, 10)
            nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1),  # 14 + 1 -5 = 10为此时输入层的大小
            nn.Sigmoid(),
            # C4最大池化 (-1, 16, 5, 5)
            nn.MaxPool2d(kernel_size=2, stride=2), # 可以认为kernel_size和stride是绑定相同的，因为移动的区域一般不重复，否则数据就泄露了
            # 进行展开，平铺成向量(-1, 16 * 5 * 5)
            nn.Flatten(),
            # C5全连接，一共三层
            nn.Linear(in_features=16 * 5 * 5, out_features=120),
            nn.Sigmoid(),
            # C6全连接，输出长度为84的向量
            nn.Linear(in_features=120, out_features=84),
            nn.Sigmoid(),
            # C7全连接，输出为10的向量，分别对应每一个数字的概率，最后实现预测
            nn.Linear(in_features=84, out_features=10)
        )

        # 这个X一定要在未实例化对象前创建，因为实例化对象之后，就会导致LeNet不可迭代，而children只能输出其最后一层的尺寸，
        self.model_layer(size=(1, 1, 28, 28))

    def forward(self, x):
        return self.model(x)

    def model_layer(self, size: tuple):
        X = torch.rand(size=size, dtype=torch.float32)  # 作为输入，
        for layer in self.model:  # 经过模型的每一层
            X = layer(X)
            # 输出组成为， 层名 + 输出大小
            print(layer.__class__.__name__, "output shape:", X.shape)

"""运行结果如下，非常直观的看到每一层神经网络结构"""
Conv2d output shape: torch.Size([1, 6, 28, 28])
Sigmoid output shape: torch.Size([1, 6, 28, 28])
MaxPool2d output shape: torch.Size([1, 6, 14, 14])
Conv2d output shape: torch.Size([1, 16, 10, 10])
Sigmoid output shape: torch.Size([1, 16, 10, 10])
MaxPool2d output shape: torch.Size([1, 16, 5, 5])
Flatten output shape: torch.Size([1, 400])
Linear output shape: torch.Size([1, 120])
Sigmoid output shape: torch.Size([1, 120])
Linear output shape: torch.Size([1, 84])
Sigmoid output shape: torch.Size([1, 84])
Linear output shape: torch.Size([1, 10])

3.2 数据处理

数据处理永远是解决任何问题中最重要的工作之一，好的数据处理能够提升模型精度，促进模型收敛等
在使用torchversion进行数据处理时非常重要！！！！
在图片处理中，主要使用transforms.Compose([操作的函数])，操作的函数如下：

Lambda(lambda x: func(x)) 和pandas中的transform作用差不多，自定义一个函数，对所有个体实行该函数
ToTensor()将其他变量如图片转换为张量，并且数据范围为(0，1)
GreyScale()灰度标准化，将三维彩色图形根据比例（经典公式 $G r a y = R * 0.299 + G * 0.587 + B * 0.114$ ）
Resize((row, col)) 负责调整大小
RandomHorizontalFlip（) 用于增强数据，随机水平翻转，并且水平翻转不会改变图像的语义（适用于大多数图像任务），可以增强模型鲁棒性
transforms.RandomCrop(32, padding=4) 用于增强数据，随机裁剪可以模拟不同的视角和位置变化，从而增强模型的泛化能力。
已知输入的图像为32x32，RandomCrop会先向外padding4个长度，使得图像大小变为36x36，再进行随机裁剪获得输出的图像32x32
transforms.Normalize(mean=[0.1, 0.2, 0.3], std=[0.5, 0.5, 0.5]), 根据输入的均值和标准差进行操作
$output=\frac{input - mean}{std}$
如果是值代表**(所有值 - 该均值) / 标准差**，如果是一个列表则代表对应位置通道下的值 - 均值 /标准差，提供不同通道对应不同的归一化


transform = transforms.Compose([
	transforms.ToTensor() 
])  # 中间输入需要对数据进行的变换，简单的话就一个ToTensor即可
mnist_train = torchvision.datasets.MNIST(root="数据集的位置", train=True, transform=transform, download=True)  # 使用download=True可以从网上下载，省去自己找数据的烦恼
mnist_test = torchvision.datasets.MNIST(root="数据集的位置", train=False, transform=transform, download=True)
dataloader_train = DataLoader(mnist_train, batch_size=64, num_workers=0, shuffle=True)
dataloader_test = DataLoader(mnist_test, batch_size=64, num_workers=0, shuffle=False)
# 这部分照抄就可以，解释一下参数
# batch_size：一次性取出的样本容量
# num_worker：0代表不使用多线程，现在cpu通常支持多线程，可以改成2，4加快数据处理，可以认为工人数量（
# shuffle：是否在每个epoch中打乱数据，训练集中True，测试集中False

3.3 （模板）设置优化器，损失函数，使用gpu(如果是N卡有cuda核心)，进行训练

这部分直接无脑照抄，没有任何技术含量，对于每一个神经网络几乎都一样
小贴士

优化器和损失函数可以根据实际需要进行修改！
epoch的选择，一开始可以让epoch大一些，接着看损失值在第n个epoch的时候几乎不变，最后将epoch改在n前面，通过早停的方法让模型不会过拟合！！！

lenet = LeNet()  # 实例化模型
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")  # 照抄，查询是否有cuda核心，有则device就是cuda，没有就是pua（
optimiser = optim.Adam(lenet.parameters(), lr=learning_rate)  # 优化器，一般使用Adam
loss_fn = nn.CrossEntropyLoss()  # 损失函数，都是模板都是模板

epoch = 10  # 可随时修改
lenet.to(device)  # 将模型挪入对应device
loss_fn.to(device)
lenet.train()  # 转换为训练模式
for i in range(epoch):  # 每一轮都会遍历整个训练集
    train_loss = 0  # 每一轮次清空损失
    start = time.time()  # 开始时间，计算
    for data in trainloader:
        image, label = data
        image = image.to(device)  # x和label都要挪入device！！！因为模型已经挪入device，不在相同device是会报错的
        label = label.to(device)

        output = lenet(image)  # 获得输出
        loss = loss_fn(output, label)  # 计算损失
        optimiser.zero_grad()  # 优化器清空梯度
        loss.backward()  # 反向传播
        optimiser.step()  # 优化器优化
        train_loss += loss.item()  # 累计当前data损失到整个训练集在当前轮次的损失
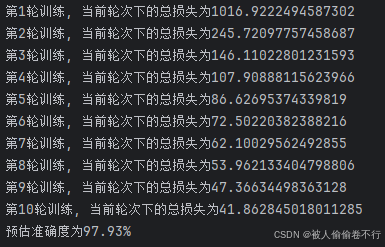
    print(f"第{i + 1}轮训练, 当前轮次下的总损失为{train_loss}\n预估剩余时间为{(epoch - i) * (time.time() - start) / 60:.2f}分钟")

torch.save(lenet, "cifar10_lenet.pkl")

3.4 进行验证

因为不同的数据集通常验证的方式也不太相同，所以这里给出我的验证方法啦

lenet.eval()  # 先转换为评估模式，仅保留权重
right = 0  # 正确数量
total = len(testloader) * 64  # 因为batch_size=64，这意味着每样本单位数量是64，总数量为样本数量乘于样本单位
for data in testloader:
    image, label = data
    image = image.to(device)
    label = label.to(device)

    outputs = [i.argmax() for i in lenet(image)]  # 因为没用softmax，最终输出的向量，其值代表的是选择的可信程度，如[0.1, 0.2],选索引0的可信程度为0.1，选索引1的可信程度为0.2，所以选择索引1
    right += sum([1 for i, j in list(zip(outputs, label)) if i == j]) # 其实就是计算 输出==标签的数量，计算测试集中总正确数量，以此计算准确度
print(f"预估准确度为{right / total * 100:.2f}%")

在这里插入图片描述
请添加图片描述
在入门测试集上精度还是很高滴，接下来拿更难的测试集练练手

四、CIFAR10实战

还是要先观察数据！！！知己知彼才有可能赢
CIFAR10物体彩色图（三通道rgb）识别(-1, 3, 32, 32)
经过神经网络模板的学习，我们知道重点其实在于神经网络的构建与数据处理上

题目分析

相比简单的MNIST，CIFAR10的数据为彩色图像，更高的通道意味着更复杂的数据，

所以我们在神经网络的构建上使用线性的Sigmoid激活函数可能无法达到在MNIST上的效果，在卷积核与池化的大小，与全连接层中每一层线性变换后的向量长度
而在数据的处理上我们需要思考是将彩色数据灰化还是在原来三通道的数据下进行处理，这也让数据处理变得更加复杂

与MNIST不同的改变

4.1构建神经网络（使用ReLU激活函数）

将激活函数从Sigmoid变为非线性的ReLU激活函数，使得其对数据的解释能力加强
对于卷积核，通常使用3x3或者5x5，在Conv2d中可以直接定义输出的通道数与卷积核大小
第一层卷积需要padding，使得边缘数据不被卷积消失，维持输入层大小不变
池化通常压缩为原有尺寸的 $\frac{1}{4}$ ，也就是池化kernel_size=2,步长stride=2
可以额外增加Dropout层，放入全连接层之间，随机抛弃神经元，防止过拟合

4.2数据增强与标准化

直接上代码解释，Compose内的代码在上面点我去回顾

# 提前了解训练集中每一个通道的均值和标准差，进行标准化
mean = [0.4914, 0.4822, 0.4465]  
# 也可以全部用0.5，0.5，0.5！
std = [0.2023, 0.1994, 0.2010]
transform = transforms.Compose([
    transforms.RandomHorizontalFlip(),  # 采用随机水平反转，水平翻转不会改变图像的语义（适用于大多数图像任务）
    transforms.RandomCrop(32, padding=4), # 采用随机裁剪可以模拟不同的视角和位置变化，从而增强模型的泛化能力。
    transforms.ToTensor(),
    transforms.Normalize(mean, std)
])

4.3灰化处理

灰化本质上也是Compose内的代码，transforms.Grayscale()，现在讲一下其可能的作用原理

灰度图输入只移除了颜色通道（从3通道到 1通道），但低级和中级特征仍然存在，因此对数据精度影响较小
LeNet-5结构简单，降低维度有助于简单模型拟合

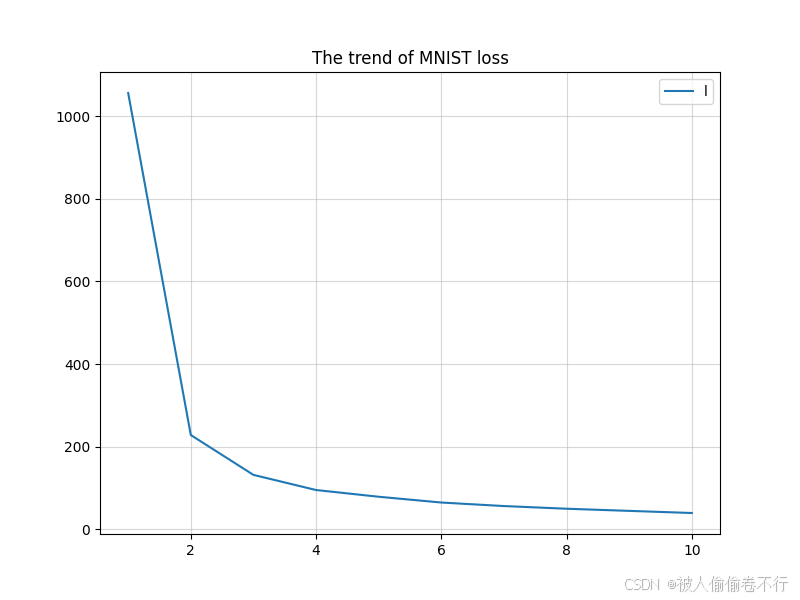
但是使用降低了维度也容易过拟合，如下图所示
请添加图片描述

虽然训练集上的损失很小，但是测试集中的准确度却不高，说明模型在测试集上过拟合

4.4全代码

import os.path
import time
import torch
import torchvision
from matplotlib import pyplot as plt
from torch.utils.data import DataLoader
from torchvision import transforms
from torch import nn, optim
import numpy as np
import random

random.seed(42)
np.random.seed(42)
torch.manual_seed(42)

class LeNet(nn.Module):
    def __init__(self, *args, **kwargs):
        super().__init__()
        self.module = nn.Sequential(
            # 输入为(-1, 3, 32, 32)
            # C1卷积层，一般输出通道数量会逐渐翻倍，所以这里从16开始
            nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, stride=1, padding=1),
            nn.ReLU(),
            # C2最大池化，输入为(-1, 16, 32, 32)
            nn.MaxPool2d(kernel_size=2, stride=2),
            # C3卷积层，输入为(-1, 16, 16, 16)
            nn.Conv2d(in_channels=16, out_channels=32, kernel_size=3, stride=1),
            nn.ReLU(),
            # C4最大池化，输入为(-1, 32, 14, 14)
            nn.MaxPool2d(kernel_size=2, stride=2),
            # C5全连接，输入为(-1, 32, 7, 7)
            nn.Flatten(),
            nn.Linear(in_features=32 * 7 * 7, out_features=224),
            nn.ReLU(),
            nn.Linear(in_features=224, out_features=96),
            nn.ReLU(),
            nn.Linear(in_features=96, out_features=10)
        )

        X = torch.rand((1, 3, 32, 32), dtype=torch.float32)
        for layer in self.module:
            X = layer(X)
            print(layer.__class__.__name__, "shape=", X.shape)

    def forward(self, x):
        return self.module(x)

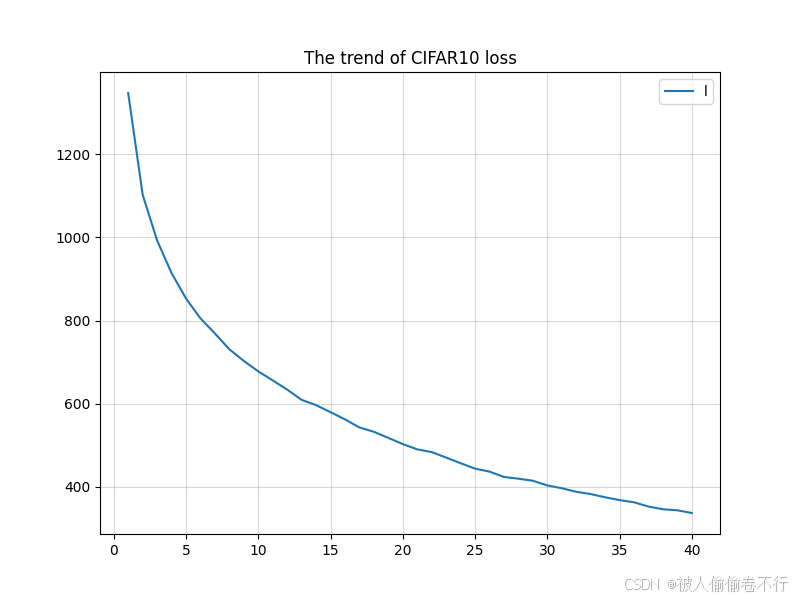
def plot_loss(epoch, total_loss):
    """负责打印损失函数趋势"""
    plt.figure(figsize=(8, 6))
    plt.plot(range(1, epoch + 1), list(map(int, total_loss)))
    plt.grid(alpha=0.5)
    plt.legend("loss")
    plt.title("The trend of CIFAR10 loss")
    plt.show()

mean = [0.4914, 0.4822, 0.4465]
std = [0.2023, 0.1994, 0.2010]
epoch = 14
learning_rate = 0.001
flag = False

lenet = LeNet()
# transform = transforms.Compose([
#     transforms.ToTensor(),
#     transforms.Normalize(mean, std)])  # 用于数据转换，使用Compose可以将一系列转换组合，定义多个转换
transform = transforms.Compose([
    transforms.RandomHorizontalFlip(),
    transforms.RandomCrop(32, padding=4),
    transforms.ToTensor(),
    transforms.Normalize(mean, std)
])
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
optimiser = optim.Adam(lenet.parameters(), lr=learning_rate, weight_decay=1e-4)
loss_fn = nn.CrossEntropyLoss()

# 数据处理
trainset = torchvision.datasets.CIFAR10(root='dataset/', train=True, download=False, transform=transform)
trainloader = DataLoader(trainset, batch_size=64, num_workers=0, shuffle=True)
testset = torchvision.datasets.CIFAR10(root='dataset/', train=False, download=False, transform=transform)
testloader = DataLoader(testset, batch_size=64, num_workers=0, shuffle=False)

lenet.to(device)
loss_fn.to(device)
lenet.train()  # 转换为训练模式

if flag:
    total_loss = []
    for i in range(epoch):
        train_loss = 0
        start = time.time()
        for data in trainloader:
            image, label = data
            image = image.to(device)
            label = label.to(device)

            output = lenet(image)
            loss = loss_fn(output, label)
            optimiser.zero_grad()
            loss.backward()
            optimiser.step()
            train_loss += loss.item()
        if not os.path.isdir("res/CIFAR10"):
            os.mkdir("res/CIFAR10")
        total_loss.append(train_loss)
        print(f"第{i + 1}轮训练, 当前轮次下的总损失为{train_loss}\n预估剩余时间为{(epoch - i) * (time.time() - start) / 60:.2f}分钟")
    torch.save(lenet, "res/CIFAR10/cifar10_rgb.pkl")
    np.save("res/CIFAR10/cifar10_rgb_loss.npy", total_loss)

else:
    loss = np.load("res/CIFAR10/cifar10_rgb_loss.npy")
    plot_loss(len(loss), loss)
    lenet = torch.load("res/CIFAR10/cifar10_rgb.pkl")


lenet.eval()
right = 0
total = len(testloader) * 64
for data in testloader:
    image, label = data
    image = image.to(device)
    label = label.to(device)

    outputs = [i.argmax() for i in lenet(image)]  # 一组data为batch_size=64
    right += sum([1 for i, j in list(zip(outputs, label)) if i == j])
print(f"预估准确度为{right / total * 100:.2f}%")

小贴士：因为深度学习跑的时间真的很久，而且放电脑上跑风扇嗡嗡响，这里就加载之前运行的模型结果啦。
最后准确度为

4.4 优化建议

总而言之，LeNet-5结构比较简单，对于复杂一点的数据集就难以应付，一步一步的思考优化能达到的最高结果也仅能达到72%
可以在增加正则化层，修改神经网络卷积层中卷积核的尺寸与输出通道数进一步优化模型拟合精度。
CIFAR10恐怖如斯，LeNet拼劲全力难以战胜，接下来登场的是更高级复杂的模型
使用ResNet等（下一篇学习笔记预告~）还有更高级的模型等待探索

总结

点我回到目录
入门深度学习的新手村，了解了卷积神经网络中的基本概念后，打了两个BOSS MNIST和CIFAR10，在MNIST效果极佳，而CIFAR10则难以胜任。需要继续深入学习，使用更高级的模型。