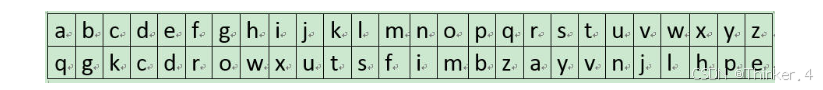文章目录
栈
首先要明确,我们快速教程的目的是快速学习或期末复习,而不是详细学习。那就要有的放矢,明确方法,注重封装。
当然,每个人有每个人不同的学习方法。这里的教程内容是最基本的内容,是必须要完全掌握的,多的部分可以了解,考试无所谓。也就是说,这里的内容完全掌握,考试可以基本全对,但是这里的内容都没掌握,考试可能无法通过。至少对于BUAA的DS考试是这样。封装和简明快速教程的特点就是这样。
具体来说,**凡是栈,我们使用数组存储。凡是队列,我们采用链表存储。**为了防止循环队列的麻烦。
定义
栈,就是后进先出,LIFO.
栈(Stack)是一种只允许在表的一端进行插入操作和删除操作的线性表。允许操作的一端称为栈顶,栈顶元素的位置由一个称为栈顶位置的变量给出。当表中没有元素时,称之为空栈。
我们使用顺序栈。链栈以防万一我们放到最后作为储备。
建立、初始化、判空、判满
#define MAXSIZE 1000
ElemType STACK[MAXSIZE];
int Top;
void initStack(){
Top = –1;
}
int isEmpty(){
return Top == –1;
}
int isFull(){
return Top == MAXSIZE–1;
}
建立栈的部分要作为全局变量。
进栈,出栈
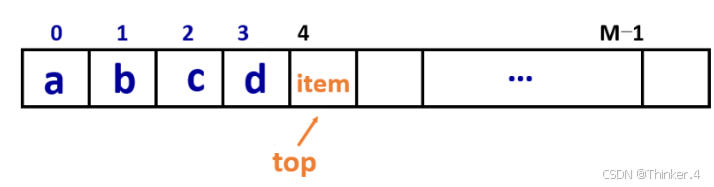
注意,这里top位置是有元素的,正好是栈顶。这是和后面的队列的本质区别。
void push(ElemType s[], ElemType item) {
//在栈s顶部压入item元素
if (!isFull()) {
s[++Top] = item;
}
}
ElemType pop(ElemType s[]){
if (!isEmpty()) {
return s[Top--];
}
}
看情况,如果不用返回栈顶元素,直接Top–扔掉也行。
关于共享栈就了解一下,可以详见BUAA的ppt。
链式存储简介
链表的特点就是没有上限个数。同样的功能我们以防万一给一下链式存储正确封装代码:
typedef struct _node {
ElemType data;
struct _node* next;
}Node;
Node* Top;
void initStack(){
Top = NULL;
}
int isEmpty(){
return Top == NULL;
}
void push(ElemType item){
Node* p = (Node*)malloc(sizeof(Node));
p->data = item;
p->next = Top;
Top = p;
}
ElemType pop(){
Node* p;
ElemType item;
if (!isEmpty()) {
p = Top;
item = Top->data;
Top = Top->next;
free(p);
return item;
}
}
这里一定要理解,指针形象上是“从右往左”指的。
应用1—计算器
中缀转后缀
从左至右遍历中缀表达式中每个数字和符号,BUAA的ppt对这里讲的比较不清不楚。下面我们详细总结规则:
首先,我们要建立一个符号栈。然后读入中缀表达式,一个一个字符遍历的读入。如果:
- 字符为 运算数 :
**直接输出,**作为后缀表达式的一部分。注意,首先要分析出完整的运算数是什么,即,如果是两位数,三位数…要学会用字符形式读取并转化为相应的十进制高位数。这是C语言最基本的问题。
- 字符为 左括号“(” :
**直接压栈。**左括号比较特殊。左括号入栈后优先级降至最低。
- 字符为 右括号“)”:
不对右括号做任何操作,然后对于栈中已有的字符:直接出栈,并将出栈字符依次输出,成为后缀表达式的一部分,直到栈顶字符为左括号(左括号也要出栈,但不送入后缀表达式)。也就是说,后缀表达式中没有左括号也没有右括号。
- 字符为 操作符(运算符,加减乘除) :
若栈空,直接入栈。若栈非空,判断栈顶操作符,若栈顶操作符优先级严格低于该操作符,该操作符入栈;否则一直出栈,并将出栈字符依次直接输出,作为后缀表达式的一部分,直到栈空或栈顶操作符优先级低于该操作符,该操作符再入栈。
也就是说,要保证入栈的操作符是全栈中最强的(优先级最高),能保证“封住”整个栈(这是形象理解)。
但是,细心的你可能会发现一点矛盾:左括号优先级最低,为什么直接压栈?因为我们这里只对操作符的情况,左括号真的比较特殊。
重复以上步骤直至遍历完成中缀表达式,接着判断符号栈是否为空,非空则依次直接出栈,并将出栈字符依次输出,直接作为后缀表达式的一部分。
我们看一下中缀转后缀的完整代码:
输入一个表达式,以“=”作为输入结束的标志,将其转为后缀表达式。
样例输入:2*(3+5)+7/1-4=
样例输出:*235+71/+4-
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <stdlib.h>
typedef struct _Op {
//每个运算符都有优先级,该结构体用于存储符号
char sign;
int pri; //用int数来量化优先级
}Op;
Op OperandStack[100]; //符号栈
int topOp = -1;
void push(char c);
Op pop();
void swiftRear();
int main()
{
swiftRear();
return 0;
}
void push(char c) {
Op operand;
operand.sign = c;
if (c == '+' || c == '-') {
operand.pri = 1;
}
else if (c == '*' || c == '/') {
operand.pri = 2;
}
else if (c == '(') {
operand.pri = 0; //注意,左括号入栈后优先级最低
}
OperandStack[++topOp] = operand;
}
Op pop() {
//注意,调用的时候要注意是不是空栈,我们在调用时判断
return OperandStack[topOp--];
}
void swiftRear() {
char c;
int digit = 0;
while (c = getchar()) {
digit = 0;
if (isdigit(c)) {
while (isdigit(c)) {
digit = digit * 10 + c - '0';
c = getchar();
}
printf("%d", digit);
//这里往后多读了一个符号,因此不能continue
}
//等于号程序结束
if (c == '=') {
break;
}
//左括号,直接压栈
if (c == '(') {
push(c);
continue;
}
//右括号,依次出栈直到左括号
if (c == ')') {
Op temp;
do {
temp = pop();
if (temp.sign != '(') {
printf("%c", temp.sign);
}
} while (temp.sign != '(');
continue;
}
//四则运算
if (c == '+' || c == '-') {
while (topOp != -1 && OperandStack[topOp].pri >= 1) {
Op temp = pop();
printf("%c", temp.sign);
}
push(c);
continue;
}
if (c == '*' || c == '/') {
while (topOp != -1 && OperandStack[topOp].pri >= 2) {
Op temp = pop();
printf("%c", temp.sign);
}
push(c);
continue;
}
}
//清空符号栈
while (topOp != -1) {
printf("%c", OperandStack[topOp--].sign);
}
}
如果用字母代替数字(代数形式输入),只需要把isdigit改成isalpha就可以。
计算后缀表达式
从左至右依次遍历后缀表达式各个字符(需要准备一个运算数栈存储运算数和操作结果),详细规则:
- 字符为 运算数 :
直接入栈。
- 字符为 操作符 :
连续出栈两次,得到两个数字。使用出栈的两个数据进行相应计算,并将计算结果入栈。这里特别要注意的是,有的二元运算是有序的(比如除法)。要看好是那个数除以那个数。应该是后出栈的数除以先出栈的数。
再比如,第一个出栈的运算数为 a ,第二个出栈的运算数为 b ,此时的操作符为 - ,则计算 b-a (注:a和b顺序不能反),并将结果入栈。
重复以上步骤直至遍历完成后缀表达式,最后栈中的数据就是中缀表达式的计算结果。
在实际操作中,我们通常会把中缀转后缀和后缀计算同时进行 。所以,会得到交叉的代码。下面给出一个例子(BUAA作业题):
【问题描述】
从标准输入中读入一个算术运算表达式,如:24 / ( 1 + 5/3 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 )= ,计算表达式结果,并输出。
要求:
1、表达式运算符只有+、-、*、/,表达式末尾的=字符表示表达式输入结束,表达式中可能会出现空格;
2、表达式中会出现圆括号,括号可能嵌套,不会出现错误的表达式;
3、表达式中出现的操作数都是十进制整数常量;但要求运算结果为浮点型,例如:5/2结果应为2.5。
4、要求采用逆波兰表达式来实现表达式计算
【输入形式】
从键盘输入一个以=结尾的算术运算表达式。操作符和操作数之间可以有空格分隔。
【输出形式】
在屏幕上输出计算结果,小数点后保留两位有效数字。
【样例输入】
24 / ( 1 + 5/3 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 ) =
【样例输出】
19.64
【样例说明】
按照运算符及括号优先级依次计算表达式的值。
【评分标准】
该题要求采用逆波兰表达式实现表达式运算,提交程序名为cal.c。
完整代码:
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <stdlib.h>
typedef struct _Op {
//每个运算符都有优先级,该结构体用于存储符号
char sign;
int pri; //用int数来量化优先级
}Op;
Op OperandStack[100]; //符号栈
int topOp = -1;
double DigitStack[100]; //数字栈
int topDigit = -1;
void push(char c);
Op pop();
void swiftRear();
void Calculate(char c);
int main()
{
swiftRear();
return 0;
}
void push(char c) {
Op operand;
operand.sign = c;
if (c == '+' || c == '-') {
operand.pri = 1;
}
else if (c == '*' || c == '/') {
operand.pri = 2;
}
else if (c == '(') {
operand.pri = 0; //注意,左括号入栈后优先级最低
}
OperandStack[++topOp] = operand;
}
Op pop() {
//注意,调用的时候要注意是不是空栈,我们在调用时判断
return OperandStack[topOp--];
}
void Calculate(char c) {
double rearNum = DigitStack[topDigit--];
double frontNum = DigitStack[topDigit--];
double result;
switch (c)
{
case '+':
result = frontNum + rearNum; break;
case '-':
result = frontNum - rearNum; break;
case '*':
result = frontNum * rearNum; break;
case'/':
result = frontNum / rearNum; break;
default:
break;
}
//进入数字栈
DigitStack[++topDigit] = result;
}
void swiftRear() {
char c;
int digit = 0;
while (c = getchar()) {
digit = 0;
if (isdigit(c)) {
while (isdigit(c)) {
digit = digit * 10 + c - '0';
c = getchar();
}
DigitStack[++topDigit] = (double)digit; //压入数字栈
//这里往后多读了一个符号,因此不能continue
}
//等于号程序结束
if (c == '=') {
break;
}
//左括号,直接压栈
if (c == '(') {
push(c);
continue;
}
//右括号,依次出栈直到左括号
if (c == ')') {
Op temp;
do {
temp = pop();
if (temp.sign != '(') {
//对数字栈的顶上两个元素拿出来做运算
Calculate(temp.sign);
}
} while (temp.sign != '(');
continue;
}
//四则运算
if (c == '+' || c == '-') {
while (topOp != -1 && OperandStack[topOp].pri >= 1) {
Op temp = pop();
Calculate(temp.sign);
}
push(c);
continue;
}
if (c == '*' || c == '/') {
while (topOp != -1 && OperandStack[topOp].pri >= 2) {
Op temp = pop();
Calculate(temp.sign);
}
push(c);
continue;
}
}
//清空符号栈
while (topOp != -1) {
Op temp = OperandStack[topOp--];
Calculate(temp.sign);
}
//打印出top2仅剩的一个数字,即为最终运算结果
printf("%.2f", DigitStack[topDigit]);
}
队列
就是先进先出,FIFO。
定义
是一种只允许在表的一端进行插入操作,而在表的另一端进行删除操作的线性表。允许插入的一端称为队尾,队尾元素的位置由rear指出; 允许删除的一端称为队头, 队头元素的位置由front指出。
顺序存储简介
使用的是循环队列,防止存储空间假满。这样就比较复杂。
#define MAXSIZE 1000
ElemType QUEUE[MAXSIZE];
int Front, Rear, Count;
void initQueue(){
Front = 0;
Rear = MAXSIZE - 1;
Count = 0;
}
int isEmpty(){
return Count == 0;
}
int isFull(){
return Count == MAXSIZE;
}
void enQueue(ElemType queue[], ElemType item){
if (isFull())
Error(“Full queue!”);
else {
Rear = (Rear + 1) % MAXSIZE;
queue[Rear] = item;
Count++;
}
}
ElemType deQueue(ElemType queue[]){
ElemType e;
if (isEmpty())
Error(“Empty queue!”); /* 队空,删除失败 */
else {
e = queue[Front];
Count--; /* 队非空,删除成功 */
Front = (Front + 1) % MAXSIZE;
return e;
}
}
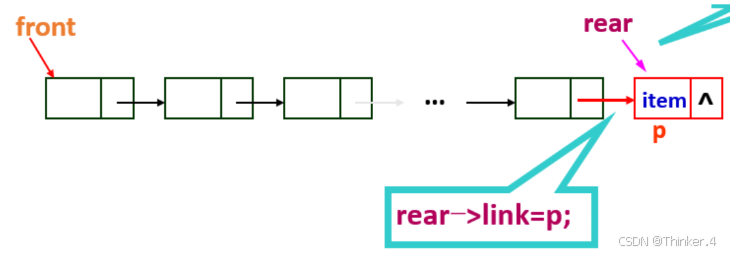
链式存储详解
为了避免循环队列逻辑不清不楚,我们推荐使用链式存储这种很直观的方式。
这里最重要的,根栈最根本的区别就是,栈的指针是“往左”指的,队列的指针是“往右”指的。
typedef struct _Node {
Elemtype data;
struct _Node* next;
}Node;
Node* Front, * Rear;
void initQueue(){
Front = NULL;
Rear = NULL;
}
int isEmpty(){
return Front == NULL;
}
void enQueue(ElemType item){
Node* p = (Node*)malloc(sizeof(Node));
p->data = item;
p->next = NULL;
if (Front == NULL) {
Front = p;
}
else {
Rear->next = p;
}
Rear = p;
}
ElemType deLQueue(){
Node* p;
ElemType item;
if (!isEmpty()) {
p = Front;
Front = Front->next;
item = p->data;
free(p);
return item;
}
}
void destroyQueue(){
while (Front != NULL) {
Rear = Front->next;
free(Front);
Front = Rear;
}
}
应用1*-函数调用关系
2020BUAA期末
- 函数调⽤关系
【问题描述】
给定某能正常运⾏结束的⽤户函数调⽤栈信息(当⼀个函数被调⽤时将⼊栈,当调⽤返回时,将出栈)。编写程序,对函数调⽤栈信息进⾏分析,依据函数⼊栈和出栈信息,分析函数调⽤关系,即⼀个函数调⽤了哪些不同函数。并按运⾏时调⽤序输出调⽤关系。
说明:
- 在⼀个函数中,同⼀函数有可能被调⽤多次,输出调⽤关系时只输出⼀次;若⼀个函数没有调⽤其它函数,则不输出调用关系;
- 函数运⾏时调⽤序是指函数在调⽤栈中的出现序。
- 程序中不存在递归调用。函数名符合C语⾔标识符的规定,函数名⻓度不超过20,每个函数最多调⽤不超过10个不同函数,程序中⽤户定义的函数个数不超过100。
算法提示:当⼀个函数⼊栈时,它就是当前栈顶函数调⽤的⼀个函数。
【输⼊形式】
假设⽤8表示函数⼊栈操作;⽤0表示当前函数出栈。当操作为8(⼊栈)时,输⼊形式为:
<操作> <函数名>
当操作为0(出栈)时,输⼊形式为:
<操作>
所有⼊栈操作和出栈操作都是从标准输⼊分⾏输⼊,假设调⽤栈中函数个数最多不超过200。开始时,调⽤栈为空,当调⽤栈再次为空时,输⼊结束。
【输出形式】
按运⾏时调⽤先后顺序输出函数调⽤关系到标准输出,每⾏为⼀个函数的调⽤关系信息,包括:函数名及被调⽤函数,函数与被调⽤函数间⽤⼀个英⽂冒号“:”分隔,被调⽤函数间⽤⼀个英⽂逗号“,”分隔,最后⼀个函数名后跟⼀个回⻋。若⼀个函数没有调⽤其它函数,则不输出。
【样例输⼊】
8 main
8 input
0
8 mysqrt
0
8 findA
0
8 findB
8 area
8 mysin
0
8 mycos
0
8 mysqrt
0
0
0
8 findC
8 area
8 mysin
0
0
8 mysqrt
8 max
0
0
0
8 output
0
0
【样例输出】
main:input,mysqrt,findA,findB,findC,ouput
mysqrt:max
findB:area
area:mysin,mycos,mysqrt
findC:area,mysqrt
【样例说明】
按照运⾏时调⽤函数的先后顺序,依次输出了main、mysqrt、findB、area和findC的函数调⽤关系。其中main函数调⽤了6个函数,按照运⾏时调⽤序依次输出。注意:mysqrt函数先于findB等函数出现在栈中,虽然mysqrt调⽤max较晚,但要先输出其调⽤关系。
//完整代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct func {
char funcName[20];
char transferFunc[10][20];
int cntTransferFunc;
int seq; // 出现次序
} Function;
Function funcs[100]; // 保存所有函数的信息
int funcIndex = 0; // 当前记录的函数总数
int stack[200]; // 调用栈,保存函数在 funcs 数组中的索引
int cntFunc = 0; // 当前栈顶位置
int findFunction(char* name) {
for (int i = 0; i < funcIndex; i++) {
if (strcmp(funcs[i].funcName, name) == 0) {
return i;
}
}
return -1;
}
int main() {
int num;
int seq = 0;
char funcName[20];
while (1) {
scanf("%d", &num);
if (num == 0) {
cntFunc--;
if (cntFunc == 0) break; // 当栈再次为空时,输入结束
}
else {
scanf(" %s", funcName);
int funcPos = findFunction(funcName);//位置
if (funcPos == -1) {
// 新函数,添加到 funcs 数组中
funcPos = funcIndex++;
strcpy(funcs[funcPos].funcName, funcName);
funcs[funcPos].cntTransferFunc = 0;
funcs[funcPos].seq = seq++;
}
if (cntFunc > 0) { // 如果当前调用栈中有函数
int callerPos = stack[cntFunc - 1]; // 获取当前栈顶函数在 funcs 数组中的位置
Function* caller = &funcs[callerPos]; // 定义一个变量,用于检查当前函数是否已经被调用过
int alreadyCalled = 0;
for (int i = 0; i < caller->cntTransferFunc; i++) { // 遍历当前栈顶函数已经记录的被调用函数列表
if (strcmp(caller->transferFunc[i], funcName) == 0) {
alreadyCalled = 1; // 如果当前函数名已经在被调用函数列表中,标记为已调用
break;
}
}
if (!alreadyCalled) { // 如果当前函数名不在被调用函数列表中,将其添加到列表中
strcpy(caller->transferFunc[caller->cntTransferFunc++], funcName);
}
}
stack[cntFunc++] = funcPos; // 将当前函数的位置索引入栈
}
}
// 按出现顺序输出函数调用关系
for (int i = 0; i < funcIndex; i++) {
if (funcs[i].cntTransferFunc > 0) {
printf("%s:", funcs[i].funcName);
for (int j = 0; j < funcs[i].cntTransferFunc; j++) {
if (j > 0) printf(",");
printf("%s", funcs[i].transferFunc[j]);
}
printf("\n");
}
}
return 0;
}
该题有一定难度,属于BUAA期末第二题的水平。
应用2-连续线段
【问题描述】
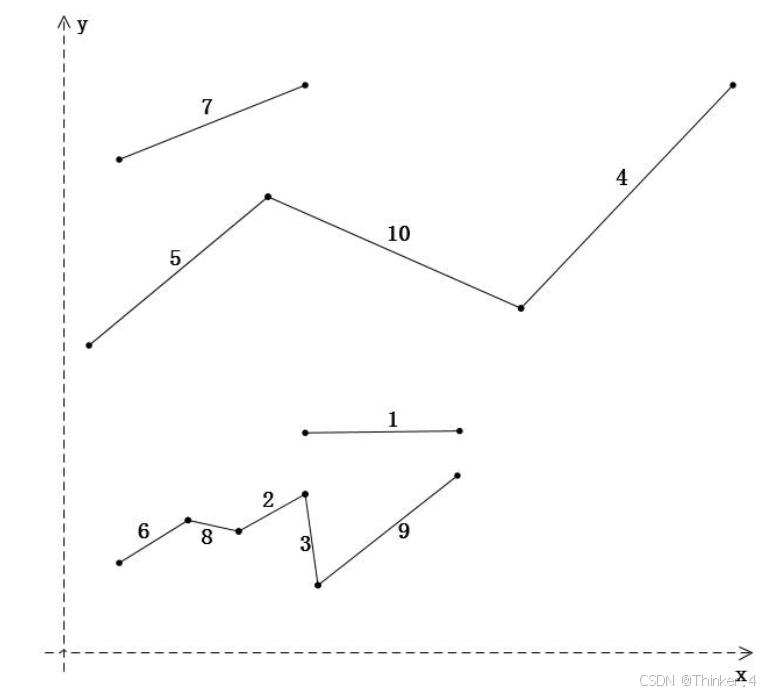
平面上两个点(一个点由(x,y)坐标组成)可构成一个线段,两个线段如果有一个端点相同,则可构成一个连续线段。假设构成线段的两个端点为v1(x1,y1)和v2(x2,y2),在此满足x1<x2,其中v1称为线段的起点,v2为线段的终点。同样,对于连续线段来说,在此满足xi<xi+1(i=1…n-1,n为连续线段中的端点数,xi为相应端点的X轴坐标)。输入一组线段(用两个端点的x、y坐标表示线段,线段个数大于等于2,小于等于100),编程计算出连续线段中包含最多线段数的线段,输出相应的线段数和起点位置(注意,不是最长的连续线段,是包含最多线段的连续线段)。例如:
上图中有10个线段,其中5、10、4号线段连成了一条连续线段,线段数3条,起点位置为5号线段的左端点;6、8、2、3、9号线段连成了另一条连续线段,该连续线段包含的线段数最多,为5条,起点位置是6号线段的左端点。
注意:
1)不考虑线段中间相交的情况;
2)不会有三条或三条以上的线段共一个端点;
3)只会出现一条包含最多线段的连续线段;
【输入形式】
先从控制台输入线段数,然后从下一行开始分行输入各线段两个端点的x、y坐标,其中第一个端点的X轴坐标小于第二个端点的X轴坐标,即x1<x2,x、y坐标都用整数表示,不会超过int的表示范围。各整数坐标值间以一个空格分隔。
【输出形式】
先在控制台输出包含最多线段数的连续线段的线段数,然后输出连续线段的起点的x、y坐标,输出数据都以一个空格分隔。
【样例输入】
10
80 75 125 75
60 40 80 55
80 55 90 20
140 120 195 205
10 111 70 165
22 35 43 43
22 175 80 205
43 43 60 40
90 20 125 60
70 165 140 120
【样例输出】
5 22 35
【样例说明】
输入了十个线段,第一个线段两个端点分别为(80,75)和(125,75),其它线段类似,如上图所示,这些线段所构成的连续线段中包含最多线段数的连续线段的线段数为5,起点为(22,35),所以输出:5 22 35。
【评分标准】
通过所有测试点将得满分。提交程序名为line.c。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
typedef struct _cor{
int x1;
int y1;
int x2;
int y2;
}Cordinate;
typedef struct _node {
Cordinate cordinate;
struct _node* next;
}Node;
int calculate(Cordinate corlist[], Cordinate cor, int num);
int findMax(int arr[], int cnt);
int main()
{
int num;
scanf("%d", &num);
int i;
Cordinate cordinate[100] = { 0 };
int sum[100] = { 0 };
for (i = 0; i < num; i++) {
scanf("%d %d %d %d", &cordinate[i].x1, &cordinate[i].y1, &cordinate[i].x2, &cordinate[i].y2);
}
for (i = 0; i < num; i++) {
sum[i] = calculate(cordinate, cordinate[i], num);
}
int loc = findMax(sum, num);//loc是sum最大的下标
printf("%d %d %d", sum[loc], cordinate[loc].x1, cordinate[loc].y1);
return 0;
}
int calculate(Cordinate corlist[], Cordinate cor, int num) {
Node* head = (Node*)malloc(sizeof(Node));
head->cordinate = cor;
head->next = NULL;
int i = 0;
int flag = 1;
while (flag) {
flag = 0;
//find the last node
Node* last = head;
while (last->next != NULL) {
last = last->next;
}
Node* p = (Node*)malloc(sizeof(Node));
for (i = 0; i < num; i++) {
if (corlist[i].x1 == last->cordinate.x2 && corlist[i].y1 == last->cordinate.y2) {
flag = 1;
p->cordinate = corlist[i];
p->next = NULL;
last->next = p;
break;
}
}
}
//calculate length
int cnt = 1;
Node* p = head;
while (p->next != NULL) {
p = p->next;
cnt++;
}
return cnt;
}
int findMax(int arr[], int cnt) {
int i = 0;
int max = arr[0];
int ret = 0;
for (i = 1; i < cnt; i++) {
if (arr[i] > max) {
max = arr[i];
ret = i;
}
}
return ret;
}
应用3-多项式相乘
【问题描述】(建议用链表实现)
编写一个程序实现两个一元多项式相乘。
【输入形式】
首先输入第一个多项式中系数不为0的项的系数和指数,以一个空格分隔。且该多项式中各项的指数均为0或正整数,系数和最高幂次不会超过int类型的表示范围。对于多项式 anxn +a n-1 x n-1 +…+ a1x1 + a0x0 的输入方法如下:
an n a n-1 n-1 … a1 1 a0 0
即相邻两个整数分别表示表达式中一项的系数和指数。在输入中只出现系数不为0的项。最后一项的指数后没有空格,只有一个回车换行符。
按照上述方式再输入第二个多项式。
【输出形式】
将运算结果输出到屏幕。将系数不为0的项按指数从高到低的顺序输出,每次输出其系数和指数,均以一个空格分隔,最后一项的指数后也可以有一个空格。
【样例输入】
10 80000 2 6000 7 300 5 10 18 0
3 6000 5 20 8 10 6 0
【样例输出】
30 86000 50 80020 80 80010 60 80000 6 12000 21 6300 10 6020 31 6010 66 6000 35 320 56 310 42 300 25 30 130 20 174 10 108 0
【样例说明】
输入的两行分别代表如下表达式:
10x80000 + 2x6000 + 7x300 + 5x10 + 18
3x6000 + 5x20 + 8x10 + 6
相乘结果为:
30x86000 + 50x80020 + 80x80010 + 60x80000 + 6x12000 + 21x6300 + 10x6020 + 31x6010 + 66x6000 + 35x320 + 56x310 + 42x300 + 25x30 + 130x20 + 174x10 + 108
提示:利用链表存储多项式的系数和指数。
【评分标准】
该题要求输出相乘后多项式中系数不为0的系数和指数,共有5个测试点。上传C语言文件名为multi.c。
题目中可能格式没有控制好,x后面的应该是幂次方,意思明白即可。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
typedef struct _multi {
int coe;
int exp;
struct _multi* next;
}Node;
Node* add(Node* head, int coe, int exp);
void cal(Node* head1, Node* head2);
void sort(Node* head);
int main()
{
Node* head1 = NULL;
Node* head2 = NULL;
int coe;
int exp;
do {
scanf("%d", &coe);
scanf("%d", &exp);
head1 = add(head1, coe, exp);
} while (getchar()!='\n');
do {
scanf("%d", &coe);
scanf("%d", &exp);
head2 = add(head2, coe, exp);
} while (getchar() != '\n');
cal(head1, head2);
return 0;
}
Node* add(Node* head, int coe, int exp) {
//create the p Node
Node* p = (Node*)malloc(sizeof(Node));
p->coe = coe;
p->exp = exp;
p->next = NULL;
//find the last,拼接
Node* last = head;
if (last != NULL) {
while (last->next != NULL) {
last = last->next;
}
last->next = p;
}
else {
head = p;
}
return head;
}
void sort(Node* head) {
Node* p, *q;
for (p = head; p->next != NULL; p = p->next) {
for (q = p->next; q != NULL; q = q->next) {
if (p->exp < q->exp) {
int tempCoe = p->coe;
p->coe = q->coe;
q->coe = tempCoe;
int tempExp = p->exp;
p->exp = q->exp;
q->exp = tempExp;
}
}
}
}
void cal(Node* head1, Node* head2) {
Node* p = head1;
Node* q = head2;
Node* headResult = NULL;
int flag = 0; //默认找不到
for (p = head1; p != NULL; p = p->next) {
for (q = head2; q != NULL; q = q->next) {
Node* temp = (Node*)malloc(sizeof(Node));
temp->coe = p->coe * q->coe;
temp->exp = p->exp + q->exp;
temp->next = NULL;
//find the last,查重并拼接
Node* last = headResult;
if (last != NULL) {
flag = 0;
while (last->next != NULL) {
if (last->exp == temp->exp) {
last->coe += temp->coe;
flag = 1;
goto here;
}
last = last->next;
}
if (last->exp == temp->exp) {
last->coe += temp->coe;
flag = 1;
}
if (flag == 0) {
last->next = temp; //没合并同类项,后边加
}
here:;
}
else {
headResult = temp;
}
}
}
//sort
sort(headResult);
//output
for (p = headResult; p != NULL; p = p->next) {
printf("%d %d ", p->coe, p->exp);
}
}
应用4-空间空闲申请模拟(最佳适应)
【问题描述】
在操作系统中,空闲存储空间通常以空闲块链表方式组织,每个块包含块起始位置、块长度及一个指向下一块的指针。空闲块按照存储位置升序组织,最后一块指向第一块(构成循环链表)。当有空间申请请求时,按照如下原则在空闲块循环链表中寻找并分配空闲块:
1)从当前位置开始遍历空闲块链表(初始是从地址最小的第一个空闲块开始),寻找满足条件的最小块(即:大于等于请求空间的最小空闲块,如果有多个大小相同的最小空闲块,则选择遍历遇到的第一个空闲块)(最佳适应原则);
2)如果选择的空闲块恰好与请求的大小相符合,则将它从链表中移除并返回给用户;这时当前位置变为移除的空闲块指向的下一空闲块;
3)如果选择的空闲块大于所申请的空间大小,则将大小合适的空闲块返回给用户,剩下的部分留在空闲块链表中;这时当前位置仍然为该空闲块;
4)如果找不到足够大的空闲块,则申请失败;这时当前位置不变。
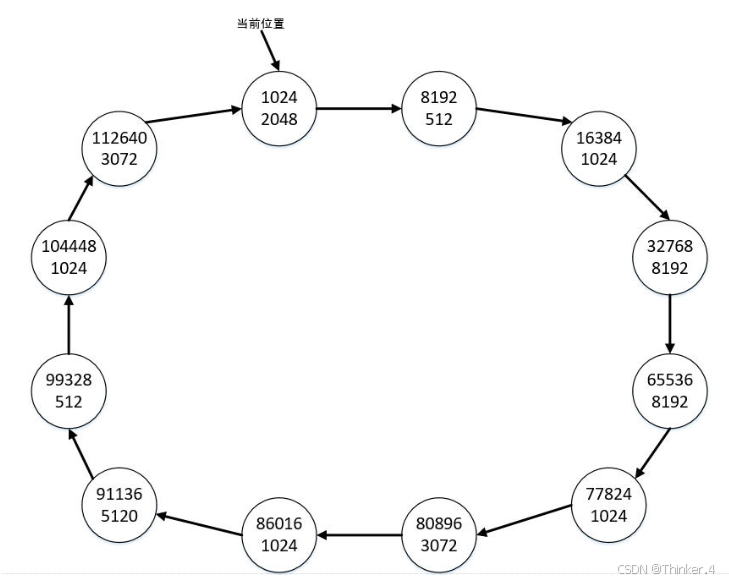
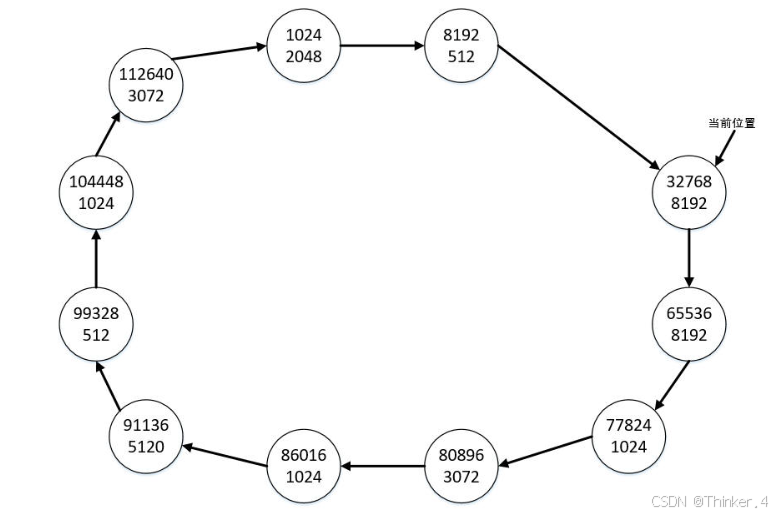
例如:下图示例给出了空闲块链表的初始状态,每个结点表示一个空闲块,结点中上面的数字指空闲块的起始位置,下面的数字指空闲块的长度,位置和长度都用正整数表示,大小不超过int表示范围。当前位置为最小地址为1024的空闲块。
若有4个申请空间请求,申请的空间大小依次为:1024、2560、10240和512。则从当前位置开始遍历上图的链表,按照上述原则寻找到满足条件的最小块为地址是16384的空闲块,其长度正好为1024,所以将其从链表中删除,这时链表状态如下图所示,当前位置变成地址为32768的空闲块。
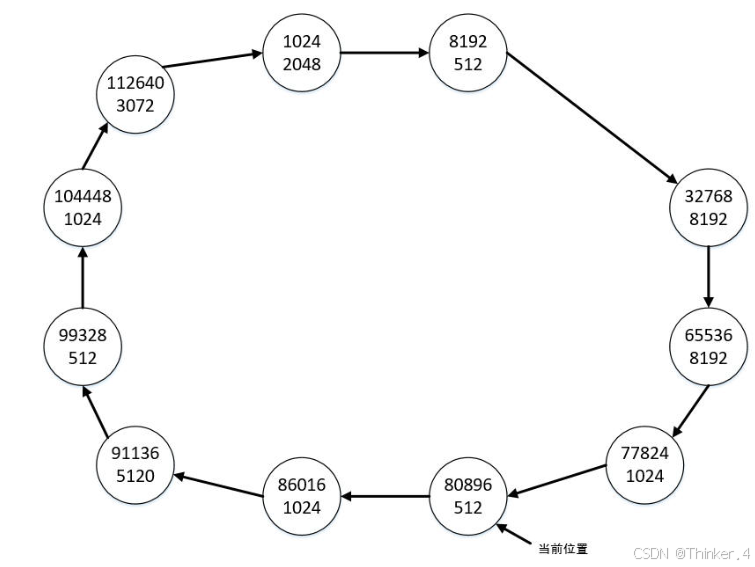
从当前位置开始为第二个空间请求(大小为2560)遍历链表,按照上述原则寻找到满足条件的最小块为地址是80896的空闲块,其长度为3072,大于请求的空间大小,于是申请空间后该空闲块剩余的长度为512,当前位置为地址是80896的空闲块,链表状态如下图所示:
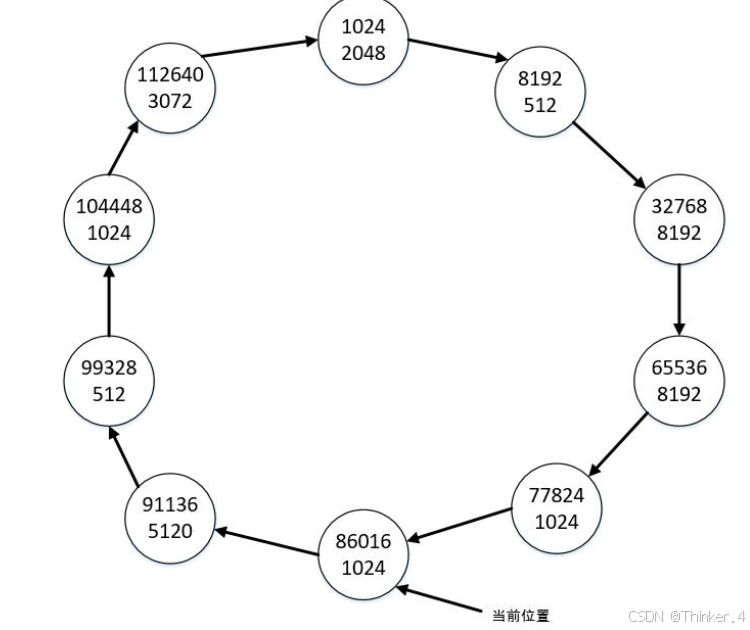
从当前位置开始为第三个空间请求(大小为10240)遍历链表,遍历一圈后发现找不到足够大的空闲块,则忽略该请求,当前位置不变。下面继续为第四个空间请求(大小为512)遍历链表,按照上述原则寻找到满足条件的最小块为当前位置的空闲块,其长度等于请求的空间大小,于是将该空闲块删除后,链表状态变为下图所示:
编写程序,模拟上述空闲空间申请。
【输入形式】
先从控制台读入一正整数,表示当前空闲块的个数(大于0且小于等于100)。
然后按照起始位置由小到大的顺序分行输入每个空闲块的起始位置和长度,位置和长度都用正整数表示,大小不超过int表示范围,两整数间以一个空格分隔。
最后在新的一行上依次输入申请空间的大小,以-1表示结束,各整数间以一个空格分隔,申请请求的个数不超过100个。
【输出形式】
按照上述原则模拟完空闲空间申请后,输出当前空闲空间链表状态,即从当前位置开始,遍历链表,分行输出剩余空闲块的起始位置和长度,位置和长度间以一个空格分隔。若申请完后,链表中没有空闲块,则什么都不输出。
【样例输入】
12
1024 2048
8192 512
16384 1024
32768 8192
65536 8192
77824 1024
80896 3072
86016 1024
91136 5120
99328 512
104448 1024
112640 3072
1024 2560 10240 512 1024 6400 512 -1
【样例输出】
104448 1024
112640 3072
1024 2048
8192 512
32768 1792
65536 8192
77824 1024
91136 5120
【样例说明】
样例输入了12个空闲块的信息,形成了如上述第一个图所示的空闲块链表;然后读取了7个空间申请请求,为前4个申请请求分配空间后,空闲块链表状态为上述最后一张图所示。满足第五个请求后,将删除地址为86016的空闲块;满足第六个请求后,地址为32768的空闲块剩余长度为1792;满足第七个请求后,将删除地址为99328的空闲块,这时链表中剩余8个空闲块,当前位置为地址是104448的空闲块,从该空闲块开始依次遍历输出所有剩余空闲块的起始位置和长度。
【评分标准】
该题要求编程模拟实现空闲空间的申请,提交程序名为memory.c。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
typedef struct _space {
int loc;
int len;
struct _space* next;
}Node;
void add(int loc, int len, Node** head);
int judgeEqual(Node* head, Node** here, int length);
void applyMore(Node* head, Node** here, int length);
void apply(Node** head, int length);
void print(Node* head);
int main()
{
int num;
scanf("%d", &num);
int i;
int loc, len;
int Length;
int length[100] = { 0 };
int cnt;
Node* head = NULL;
for (i = 0; i < num; i++) {
scanf("%d %d", &loc, &len);
add(loc, len, &head);
}
//构造循环链表
Node* last = head;
while (last->next != NULL) {
last = last->next;
}
last->next = head;
i = 0;
scanf("%d", &Length);
while (Length != -1) {
length[i++] = Length;
scanf("%d", &Length);
}
cnt = i; //要申请的总个数
for (i = 0; i < cnt; i++) {
apply(&head, length[i]);
}
print(head);
return 0;
}
void add(int loc, int len, Node** head) {
Node* p = (Node*)malloc(sizeof(Node));
p->len = len;
p->loc = loc;
p->next = NULL;
//find the last node
Node* last = *head;
if (last != NULL) {
while (last->next != NULL) {
last = last->next;
}
last->next = p;
}
else {
*head = p;
}
}
int judgeEqual(Node* head, Node** here, int length) {
*here = head;
int flag = 0;
if ((*here)->len == length) {
//find last
Node* t = (*here)->next;
while (t->next != head) {
t = t->next;
}
t->next = head->next;
*here = (*here)->next;
free(head);
flag = 1;
goto exit;
}
while ((*here)->next != head) {
if ((*here)->next->len == length) {
Node* t = (*here)->next;
(*here)->next = (*here)->next->next;
free(t);
(*here) = (*here)->next;
flag = 1;
break;
}
*here = (*here)->next;
}
exit:;
return flag;
}
void applyMore(Node* head, Node** here, int length) {
*here = head;
int space[100] = { 0 };
int cnt = 0;
int i = 0;
Node* p;
for (p = head; p->next != head; p = p->next) {
if (p->len > length) {
space[i++] = p->len;
}
}
if (p->len > length) {
space[i++] = p->len;
}
cnt = i; //所有空间大于length的节点的个数
if (cnt != 0) {
//find min
int min = space[0];
for (i = 0; i < cnt; i++) {
if (space[i] < min) {
min = space[i];
}
}
while ((*here)->len != min) {
*here = (*here)->next;
}
(*here)->len -= length;
}
}
void apply(Node** head, int length) {
//三种情况,有空间相等,略大,不存在
Node* here = *head;
int flag = 0;
flag = judgeEqual(*head, &here, length);
if (flag == 0) {
applyMore(*head, &here, length);
}
*head = here;
}
void print(Node* head) {
Node* p = head;
while (p->next != head) {
if (p->loc != 0) {
printf("%d %d\n", p->loc, p->len);
p = p->next;
}
}
if (p->loc != 0) {
printf("%d %d\n", p->loc, p->len);
}
}
应用5-文件加密(环)
【问题描述】(建议用链表实现)
有一种文本文件加密方法,其方法如下:
1、密钥由所有ASCII码可见字符(ASCII码编码值32-126为可见字符)组成,密钥长度不超过32个字符;
2、先将密钥中的重复字符去掉,即:只保留最先出现的字符,其后出现的相同字符都去掉;
3、将不含重复字符的密钥和其它不在密钥中的可见字符(按字符升序)连成一个由可见字符组成的环,密钥在前,密钥的头字符为环的起始位置;
4、设原密钥的第一个字符(即环的起始位置)作为环的开始位置标识,先从环中删除第一个字符(位置标识则移至下一个字符),再沿着环从下一个字符开始顺时针以第一个字符的ASCII码值移动该位置标识至某个字符,则该字符成为第一个字符的密文字符;然后从环中删除该字符,再从下一个字符开始顺时针以该字符的ASCII码值移动位置标识至某个字符,找到该字符的密文字符;依次按照同样方法找到其它字符的密文字符。当环中只剩一个字符时,则该剩下的最后一个字符的密文为原密钥的第一个字符。
下面以可见字符集只由小写字母组成为例来说明对应密文字符集生成过程。如果密钥为:helloworld,将密钥中重复字符去掉后为:helowrd,将不在密钥中的小写字母按照升序添加在密钥后,即形成字符串:helowrdabcfgijkmnpqstuvxyz,该字符串形成的环如下图所示:
明码的第一个字母为h,h也是环的起始位置。h的ASCII码制为104,先把h从环中删除,再从下一个字母e开始顺时针沿着环按其ASCII值移动位置标识(即:在字母e为移动第1次,共移动位置标识104次)至字母w,则h的密文字符为w。w的ASCII码制为119,然后将w从环中删除,再从下一个字母r开始顺时针沿着环移动位置标识119次至字母为l,则w的密文字符为l。依次按照同样方法找到其它字母的密文字符。环中剩下的最后一个字母为x,则x的密文字符为明码的第一个字母h。按照这种方法形成的密文转换字符表为:
上方为原文字符,下方为对应的密文字符。由所有ASCII可见字符集组成的字符集密文字符生成方式与上例相同。
编写程序实现上述文件加密方法。密钥从标准输入读取,待加密文件为当前目录下的in.txt文件,该文件中的字符若是可见字符,则按照上述方法进行加密,否则原样输出(例如:回车换行符),加密后生成的密文文件为当前目录下的in_crpyt.txt。
【输入形式】
密钥是从标准输入读取的一行字符串,可以包含任意ASCII码可见字符(ASCII码编码值32-126为可见字符),长度不超过32个字符。
【输出形式】
加密后生成的密文文件为当前目录下的in_crpyt.txt。
【样例输入】
C Programming(Second Edition)
假设in.txt文件内容为:
This book is meant to help the reader learn how to program in C. It is the definitive reference guide, now in a second edition. Although the first edition was written in 1978, it continues to be a worldwide best-seller. This second edition brings the classic original up to date to include the ANSI standard.
From the Preface:
【样例输出】
in_crpyt.txt文件内容为:
KgklW#33>WklWA^M8W83Wg\Z,W8g\WP^u\PWZ^PMWg3jW83W,P30PAWkMWX5W.8WklW8g\Wu\EkMk8kt\WP\E\P\MR\W0-ku+WM3jWkMWWl\R3MuW\uk8k3M5WIZ8g3-0gW8g\WEkPl8W\uk8k3MWjlWjPk88\MWkMW’71G+Wk8WR3M8kM-\lW83W#\WWj3PZujku\W#\l8Jl\ZZ\P5WKgklWl\R3MuW\uk8k3MW#PkM0lW8g\WRZllkRW3Pk0kMZW-,W83Wu8\W83WkMRZ-u\W8g\WIOY.Wl8Mu^Pu5
4P3AW8g\WdP\E^R(
【样例说明】
输入的密钥为C Programming(Second Edition),由该密钥生成的字符串环中字符依次为:
C Progamin(SecdEt)!"#$%&'*+,-./0123456789:;<=>?@ABDFGHIJKLMNOQRTUVWXYZ[]^_`bfhjklpqsuvwxyz{|}~
形成的字符转换字符表(第一行为原ASCII字符,第二行为对应的密文字符)为:
按照该密文转换字符表将in.txt中的内容转换成加密字符输出到in_crpyt.txt中。
【评分标准】
该题要求对指定的文件进行加密,提交的文件名为:encode.c。
#include <stdio.h>
#include <string.h>
struct circle
{
char zifu;
char mifu;
int next;
int qian;
}circle[100];
char map[100],a[100],ch;
char txt[100000];
int main()
{
int i=0,j=0,len=0,flag=0,mishi=0,k=0,l=0,shu=0;
char arr[100];
gets(a);
for(i=0;i<100;i++)
{
for(j=i+1;j<100;j++)
{
if(a[i]==a[j])
{
a[j]=0;
}
}
}//去除重复字母
for(i=0,len=0;i<100;i++)
{
if(a[i]!=0)
{
map[len]=a[i];
len++;
}
}//得到新的,中间没有0的密匙
mishi=len;
flag=0;
for(i=32;i<=126;i++)
{
arr[i-32]=i;
}//得到所有可见字符
for(i=0;i<=94;i++)
{
flag=0;
for(j=0;j<mishi;j++)
{
if(arr[i]==map[j])
{
flag=1;
break;
}
else
flag=0;
}
if(flag==0)
{
map[len]=arr[i];
len++;
}
}//得到新的密匙
for(i=0;i<len;i++)
{
circle[i].zifu=map[i];
circle[i].next=i+1;
circle[i].qian=i-1;
}//建立一个链表
circle[len-1].next=0;
circle[0].qian=(len-1);//将环首尾相接
i=0;
for(l=0;l<94;l++)
{
shu=circle[i].zifu;
circle[circle[i].qian].next=circle[i].next;
circle[circle[i].next].qian=circle[i].qian;
k=i;
for(j=0;j<shu;j++)
{
circle[i].mifu=circle[circle[k].next].zifu;
k=circle[k].next;
}
i=k;
}
circle[i].mifu=circle[0].zifu;
FILE *fp,*fo;
fp=fopen("in.txt","r");
fo=fopen("in_crpyt.txt","w");
flag=0;
ch=fgetc(fp);
while(ch!=EOF)
{
if(ch>=32&&ch<=126)
{
for(i=0;i<95;i++)
{
if(ch==circle[i].zifu)
{
ch=circle[i].mifu;
fputc(ch,fo);
break;
}
}
}
else
fputc(ch,fo);
ch=fgetc(fp);
}
fclose(fp);
fclose(fo);
}
应用6-词频统计(数组或链表实现)
【问题描述】
编写程序统计一个英文文本文件中每个单词的出现次数(词频统计),并将统计结果按单词字典序输出到屏幕上。
注:在此单词为仅由字母组成的字符序列。包含大写字母的单词应将大写字母转换为小写字母后统计。
【输入形式】
打开当前目录下文件“article.txt”,从中读取英文单词进行词频统计。
【输出形式】
程序将单词统计结果按单词字典序输出到屏幕上,每行输出一个单词及其出现次数,单词和其出现次数间由一个空格分隔,出现次数后无空格,直接为回车。
【样例输入】
当前目录下文件article.txt内容如下:
“Do not take to heart every thing you hear.”
“Do not spend all that you have.”
“Do not sleep as long as you want;”
【样例输出】
all 1
as 2
do 3
every 1
have 1
hear 1
heart 1
long 1
not 3
sleep 1
spend 1
take 1
that 1
thing 1
to 1
want 1
you 3
【样例说明】
按单词字典序依次输出单词及其出现次数。
【评分标准】
通过所有测试点将得满分。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
typedef struct _node {
char word[20];
int rate;
struct _node* next;
}Node;
void add(Node** head, char word[]);
void sort(Node** head);
void print(Node* head);
int main()
{
FILE* fp = fopen("article.txt", "r");
int i, j;
char word[20] = { 0 };
char line[200] = { 0 };
Node* head = NULL;
while (fgets(line, 200, fp) != NULL) {
j = 0;
for (i = 0; i < strlen(line); i++) {
if (line[i] >= 'a' && line[i] <= 'z' || line[i] >= 'A' && line[i] <= 'Z') {
word[j++] = tolower(line[i]);
}
else {
if (word[0] != '\0') {
add(&head, word);
j = 0;
//清空word
for (int k = 0; k < 20; k++) {
word[k] = '\0';
}
}
}
}
}
fclose(fp);
sort(&head);
print(head);
return 0;
}
void add(Node** head, char word[]) {
int i;
Node* p = (Node*)malloc(sizeof(Node));
for (i = 0; i < strlen(word); i++) {
p->word[i] = word[i];
}
p->word[i] = '\0';
p->rate = 1;
p->next = NULL;
//插入链表
Node* last = *head;
if (last != NULL) {
while (last->next != NULL) {
if (strcmp(last->word, word) == 0) {
last->rate++;
goto exit;
}
last = last->next;
}
//最后一个节点
if (strcmp(last->word, word) == 0) {
last->rate++;
goto exit;
}
last->next = p;
}
else {
*head = p;
}
exit:;
}
void sort(Node** head) {
Node* p, * q;
for (p = *head; p->next != NULL; p = p->next) {
for (q = p->next; q != NULL; q = q->next) {
if (strcmp(p->word, q->word) > 0) {
//交换word
char tempWord[20] = { 0 };
strcpy(tempWord, p->word);
strcpy(p->word, q->word);
strcpy(q->word, tempWord);
//交换rate
int temp = p->rate;
p->rate = q->rate;
q->rate = temp;
}
}
}
}
void print(Node* head) {
Node* p = head;
while (p != NULL) {
printf("%s ", p->word);
printf("%d\n", p->rate);
p = p->next;
}
}
一定要擅长用isalpha/isdigit库函数。我当时不知道。初学者一定要逐步积累相关库函数,避免重复劳动。