文章目录
树
这是数据结构最重要的内容之一。本文超万字解析,不求面面俱到,但求突出重点,务实高效。
树的部分就是递归的天下。务必要掌握各种定义、递归的功能模板这种最基本的东西,在实现各种功能时多从封装代码中修改,而不是自己盲目写。
这里的内容是最核心最精简的内容,适合代码封装和期末复习。对于一些进阶内容(如线索二叉树、平衡二叉树等)不过多介绍。我们的目的是掌握最基本的内容,实现初步的应用,达到课程的要求,至少是完全覆盖考试的能力要求。
使用的方法是调用而不是细扣每一个细节。直到一个封装代码块的实现功能、什么时候用而不是每个逻辑是怎么写的。考场上短时间内写一个完全正确的递归,对于初学者而言是不现实的。
我们尽量涵盖到每一种考试可能出现的情况,因为树是高频也是最重要的考点,在图不考编程题的情况下。因此,我们尤其注重代码封装,以及不同功能的代码封装,确保能够快速直接实现功能。
所以,问题抽象的能力就是重要的,比书写代码能力更重要,在这套简明笔记的理念下。
这个部分最大的特点就是有所侧重。这意味着,已经是最简明的教程,提到的部分必须完全掌握。最基本的部分就是:
树的基本概念
树的定义
树是n(n>=0)个结点的有限集。当n = 0时,称为空树。在任意一棵非空树中应满足:
- 有且仅有一个特定的称为根的结点。
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每个集合本身又是一棵树,并且称为根的子树。
这里就可以看出,树是递归定义的。树的最本质特征是一个前驱,可以多个后继。
基本术语
- 结点的度:该结点拥有的子树的数目。就是分叉的条数。
- 树的度:树中结点的度的最大值(注意区分)。
- 叶结点:度为0的结点。
- 分支结点:度非0的结点。
- 树的层次:根结点为第1层,若某结点在第i 层,则其孩子结点(若存在)为第i+1层。注意没有第0层。
- 树的深度/高度:树中结点所处的最大层次数。
- 森林:m (m≥0)棵互不相交的树的集合。森林的概念与树的概念十分相近,因为只要把树的根结点删去就成了森林。反之,只要给m棵独立的树加上一个结点,并把这m棵树作为该结点的子树,则森林就变成了树。
输的存储分为顺序和链式。一般采用链式。下面我们着重介绍二叉树。二叉树中会介绍详细的存储。
二叉树
定义
每个结点至多只有两棵子树( 即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能任意颠倒。二叉树也以递归的形式定义。二叉树是n (n≥0) 个结点的有限集合:
- 或者为空二叉树,即n=0。
- 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
二叉树是有序树,若将其左、右子树颠倒,则成为另一棵不同的二叉树。
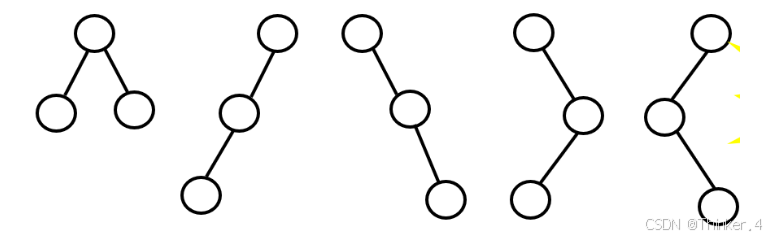
例:具有3个结点的二叉树有5种形态。但具有3个结点的树只有1种形态。
完全二叉树与满二叉树
满二叉树
若一棵二叉树中的结点,或者为叶结点, 或者具有两棵非空子树,并且叶结点都集中在二叉树的最下面一层。这样的二叉树为满二叉树。
概括起来,树中的每层都含有最多的结点。满二叉树的叶子结点都集中在二叉树的最下一层,并且除叶子结点之外的每个结点度数均为 2。
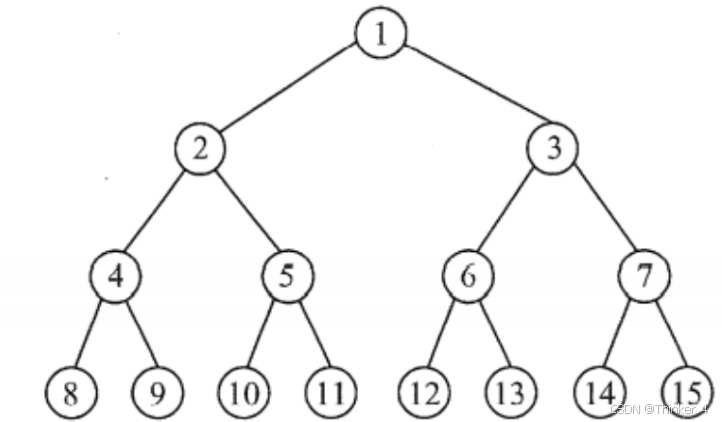
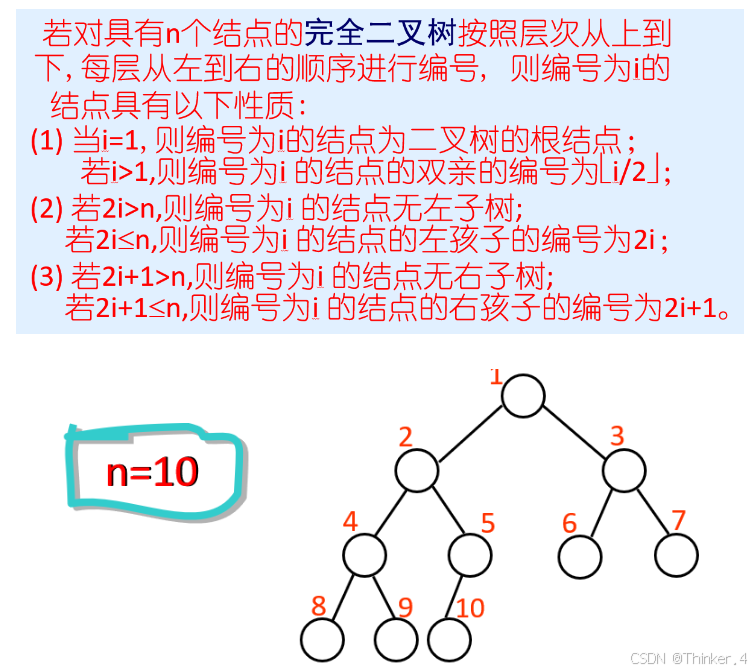
重要(选择题易考):可以对满二叉树按层序编号:约定编号从根结点(根结点编号为1)起,自上而下,自左向右。这样,每个结点对应一个编号,对于编号为i的结点,若有双亲,则其双亲为 i / 2 (向下取整),若有左孩子,则左孩子为 2i;若有右孩子,则右孩子为 2 i + 1。
完全二叉树
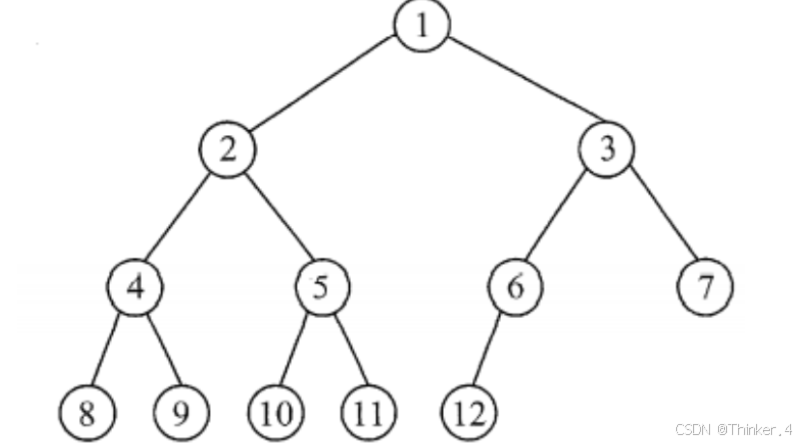
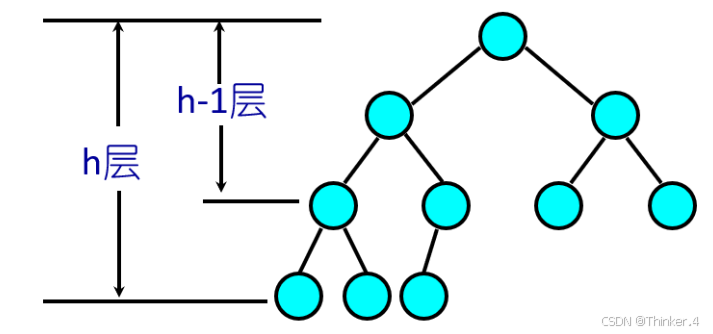
高度为 h、有 n个结点的二叉树,当且仅当其每个结点都与高度为 h 的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树,如图所示。其特点如下:
说人话:可以不满,但只能最后一层(叶结点这一层)不满。而且必须要从右往左不满。否则都不是。
有以下重要性质:
- 若 i ≤ n / 2 , 则结点 i为分支结点,否则为叶子结点。这里的n是指完全二叉树顶点的个数。比如上图中n为12.
- 叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点,都依次排列在该层最左边的位置上。
- 若有度为 1的结点,则只可能有一个,且该结点只有左孩子而无右孩子(重要特征)。
- 按层序编号后,一旦出现某结点(编号为 i )为叶子结点或只有左孩子,则编号大于 i 的结点均为叶子结点。
- 若 n 为奇数,则每个分支结点都有左孩子和右孩子;若 n为偶数,则编号最大的分支结点(编号为 n / 2 )只有左孩子,没有右孩子,其余分支结点左、右孩子都有。注意这里的n指的是完全二叉树中顶点的个数(如上图中是12),与1中的n相同。
二叉树的重要性质
这里的都非常重要:
- 具有n个结点的非空二叉树共有 n - 1 个分支。
- 非空二叉树的第i层最多有2^(i - 1)个节点。
- 深度为h的二叉树最多有2^( h ) - 1个结点。
- 若非空二叉树有n0个叶结点,有n2个度为2的结点,则 n0=n2+1。
- 具有n个结点的非空完全二叉树的深度为h=[log2n]+1.
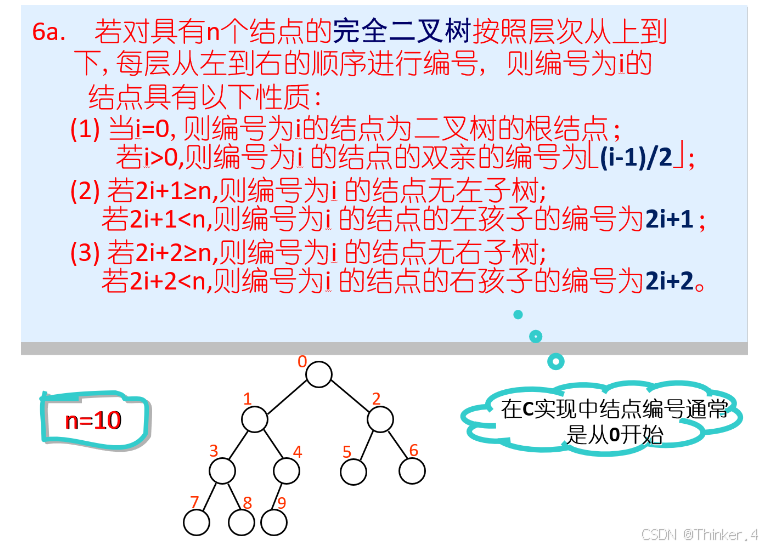
对于C语言编程而言,更多是下标从0开始,所以有以下推论(内容不变,只是下标从0开始):
二叉树的链式存储(代码)
typedef struct _Tree{
Datatype data;
struct _Tree *left, *right;
}Tree;
Tree* T;
二叉树的遍历
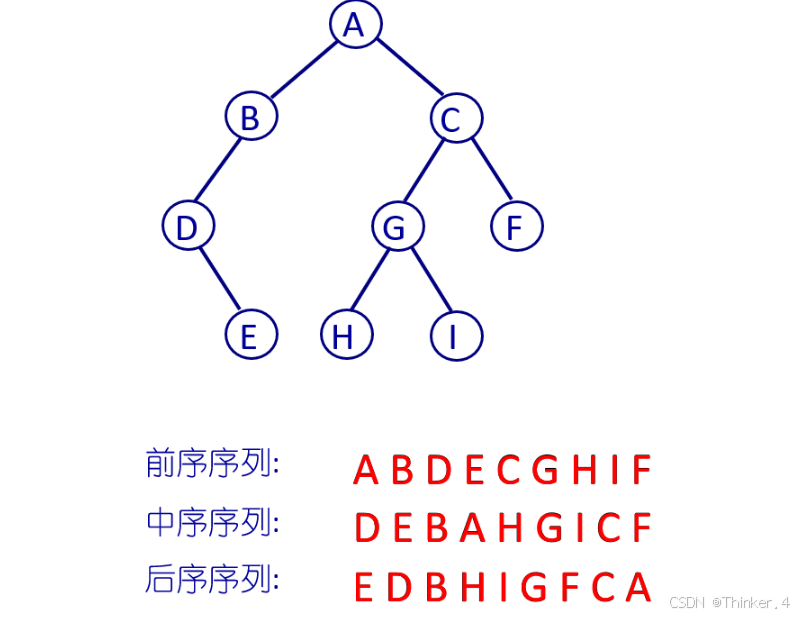
二叉树的遍历( traversing binary tree )是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。本质是递归。
三种序列的遍历指的是根节点在遍历中的顺序。根节点先遍历叫先序遍历,根节点在中间成为中序遍历,根节点最后称为后序遍历。
先看一个小知识点:
先序遍历
根——左——右
void PreOrderTraverse(Tree* t){
if (t != NULL) {
VISIT(t); /* 访问t指向结点 */
PreOrderTraverse(t->left);
PreOrderTraverse(t->right);
}
}
中序遍历
左——根——右
void InOrderTraverse(Tree* t){
if (t != NULL) {
InOrderTraverse(t->left);
VISIT(t); /* 访问t指向结点 */
InOrderTraverse(t->right);
}
}
后序遍历
左——右——根
void PostOrderTraverse(Tree* t){
if (t != NULL) {
PostOrderTraverse(t->left);
PostOrderTraverse(t->right);
VISIT(t); /* 访问t指向结点 */
}
}
层次遍历
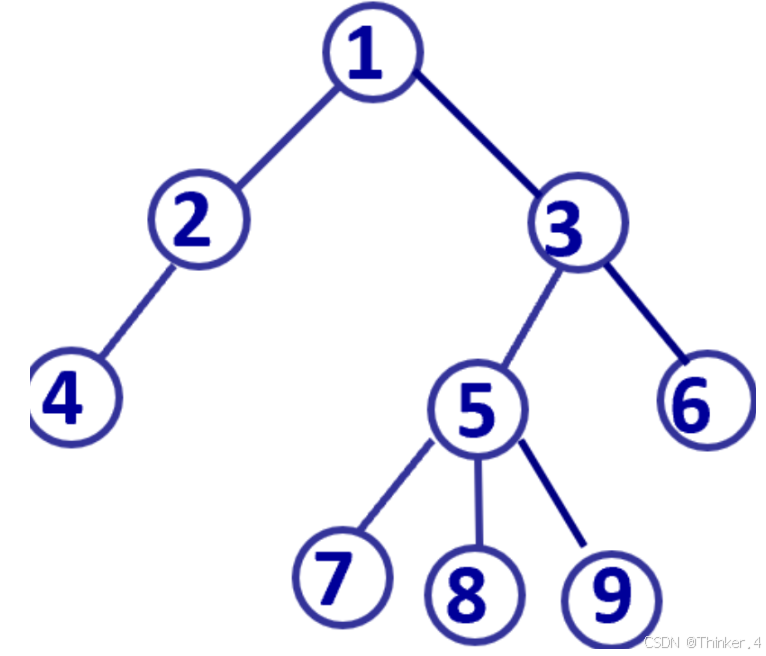
即按照箭头所指方向,按照1,2,3, 4的层次顺序,对二叉树中的各个结点进行访问。
要进行层次遍历,需要借助一个队列。先将二叉树根结点入队,然后出队,访问出队结点,若它有左子树,则将左子树根结点入队;若它有右子树,则将右子树根结点入队。然后出队,访问出队结点……如此反复,直至队列为空。
二叉树的层次遍历算法如下:
Tree* Q[100];
int front, rear;
void InitQueue(Tree* Q[]) {
front = rear = 0;
}
void EnQueue(Tree* Q[], Tree* T) {
Q[rear++] = T;
}
Tree* DeQueue(Tree* Q[]) {
return Q[front++];
}
int isEmpty(Tree* Q[]) {
return front == rear;
}
void LevelOrderTraverse(Tree* T) {
InitQueue(Q); //初始化辅助队列
Tree* p;
EnQueue(Q, T); //将根节点入队
while (!isEmpty(Q)) { //队列不空则循环
p = DeQueue(Q); //队头结点出队
visit(p); //访问出队结点
if (p->lchild != NULL) {
EnQueue(Q, p->lchild); //左子树不空,则左子树根节点入队
}
if (p->rchild != NULL) {
EnQueue(Q, p->rchild); //右子树不空,则右子树根节点入队
}
}
}
Q要定义成全局变量。层次遍历的时间复杂度是O(n)。
层次排序
是层次遍历的推广。有时候我们需要对每一层进行排序后输出。这种情况多数在多叉树中。(比如:按层次遍历序分行输出拷贝后目录树中的文件及相应日期时间,同一层的按时间序输出,若同一层的时间也相同,则按照文件名的字典序输出。注意只输出普通文件信息,不输出目录信息。)
对于这种要求。我们把需求分为两类:
- 对所有节点的孩子节点进行指标排序,然后层次输出;
- 对每一层的所有结点合在一起,进行排序后输出。
这两种有明显区别,要好好体会。
情况一
对于第一种,我们有两种方法。一是先排后遍历,即先对树进行递归的排序,再层次遍历输出。这就需要构造一个sortTree函数。首先我们来看多叉树的情况:
typedef struct _Tree {
File f; //内容类型
struct _Tree* child[100]; //所有子树
int childCount; //字数数量
}Tree;
void sortTree(Tree* root) {
if (root == NULL){
return;
}
for (int i = 0; i < root->childCount; i++) {
sortTree(root->child[i]);
}
qsort(root->child, root->childCount, sizeof(Tree*), cmp);
}
int cmp(const void* a, const void* b) { //举个例子
Tree* t1 = *(Tree**)a;
Tree* t2 = *(Tree**)b;
if (strcmp(t1->f.time, t2->f.time) == 0) {
return strcmp(t1->f.name, t2->f.name);
}
return strcmp(t1->f.time, t2->f.time);
}
**一定要注意,qsort放最后。**这是递归的口诀,否则会导致最后一层叶节点不被处理。凡是递归,qsort放在递归后!
还有一个问题就是cmp函数中t1,t2的类型,为什么一定要是Tree*而不是Tree。一定注意,这个类型与qsort中sizeof相同。 sizeof里边是Tree*,所以t1,t2也要是指针类型。
对于二叉树,会更简单一些:
void sortTree(Tree* root) {
if (root == NULL){
return;
}
sortTree(root->left);
sortTree(root->right);
//具体按照需求进行排序,只需要判断孩子是否是空,非空则交换
}
然后,调用我们的层次遍历函数直接输出即可。
第二种方法我们重点介绍,是在层次遍历时同时排序。
我们先来看多叉树:
void LevelOrderTraverse() {
int i;
Tree* p;
EnQueue(T); // 将根节点入队
while (!isEmpty()) { // 队列不空则循环
p = DeQueue(); // 队头结点出队
// 对当前层的子节点进行排序
qsort(p->child, p->childCount, sizeof(Tree*), cmp);
// 打印当前节点的信息
if (strcmp(p->f.time, "-") != 0) { //例子
printf("%s %s\n", p->f.name, p->f.time);
}
// 将当前节点的子节点入队
for (i = 0; i < p->childCount; i++) {
EnQueue(p->child[i]);
}
}
}
如果是二叉树:只需要更改排序和入队就可以了。一定要注意非空才入队。
情况二
这里更困难的就是,要把所有同一层的结点全部集中起来(不管父节点是谁,全部平等),然后把这集中起来的所有节点进行指标排序输出,形成彻底的层次遍历。
我们首先来看多叉树:
void LevelOrderTraverse() {
int i;
Tree* p;
Tree* level[1000];
int levelCount;
EnQueue(T); //将根节点入队
while (!isEmpty(Q)) { //队列不空则循环
int levelSize = rear - front; //当前层的节点数
levelCount = 0;
//提取当前层的所有节点
for (i = 0; i < levelSize; i++) {
p = DeQueue();
level[levelCount++] = p;
//将下一层的所有节点入队
for (int j = 0; j < p->childCount; j++) {
EnQueue(p->child[j]);
}
}
// 对当前层的子节点进行排序
qsort(level, levelCount, sizeof(Tree*), cmp);
//输出当前层的所有节点
for (int i = 0; i < levelCount; i++) {
if (strcmp(level[i]->f.time, "-") != 0) {
printf("%s %s\n", level[i]->f.name, level[i]->f.time);
}
}
}
}
对于二叉树:
void LevelOrderTraverse() {
int i;
Tree* p;
Tree* level[1000];
int levelCount;
EnQueue(T); //将根节点入队
while (!isEmpty(Q)) { //队列不空则循环
int levelSize = 0; //当前层的节点数
//提取当前层的所有节点
for (i = 0; !isEmpty(Q); i++) {
p = DeQueue();
level[levelSize++] = p;
//将下一层的所有节点入队
if(p->left !=NULL){
EnQueue(p->left);
}
if(p->right !=NULL){
EnQueue(p->right);
}
}
// 对当前层的子节点进行排序
qsort(level, levelSize, sizeof(Tree*), cmp);
//输出当前层的所有节点
for (int i = 0; i < levelSize; i++) {
//按需输出
}
}
}
这里的levelSize相当于多叉树的levelCount。
更多的应用例子见应用3.
中断遍历
这是一种常见的需求情况。就是使用前序遍历(或中序、后序遍历)寻找某个结点,找到之后立即停止。对于递归来说,return并不能结束整个函数。我们这里有两种方式可以采用:
方法一:使用进阶递归。
例:
Tree* PreOrderTraverse(Tree* t) {
if (t != NULL) {
if (t->cnt == max) { //示例
return t;
}
Tree* leftResult = PreOrderTraverse(t->left);
if (leftResult != NULL) {
return leftResult;
}
Tree* rightResult = PreOrderTraverse(t->right);
if (rightResult != NULL) {
return rightResult;
}
}
return NULL;
}
Tree* target = PreOrderTraverse(T);
可以直接进行指针赋值。
方法二:使用flag。
这种方法的特点是,不用过多的修改我们之前封装的函数。使用全局target和flag来记录情况。全局变量自动初始化为空。
//全局
Tree* target;
int flag;
void PreOrderTraverse(Tree* t) {
if (!flag && t != NULL) {
if (t->cnt == max) {
flag = 1;
target = t;
}
PreOrderTraverse(t->left);
PreOrderTraverse(t->right);
}
}
不论哪种方法,我们的最终目的就是把找到的第一个符合条件的target指针记录下来。target指针可以直接指向所需节点的所有内容。
树的搜索与插入
二叉树无脑搜索:
// 在二叉树中搜索某个值
Tree* search(Tree* root, int target) {
if (root == NULL) {
return NULL;
}
if (root->data == target) {
return root;
}
Tree* result = search(root->left, target);
if (result != NULL) {
return result;
}
return search(root->right, target);
}
返回的是某个树节点的指针,可以直接赋值给变量,比如Tree* tar = search(T, target)同理推广到三叉树:
// 在三叉树中搜索某个值
Tree* search(Tree* root, int target) {
if (root == NULL) {
return NULL;
}
if (root->data == target) {
return root;
}
Tree* result = search(root->left, target);
if (result != NULL) {
return result;
}
result = search(root->mid, target);
if (result != NULL) {
return result;
}
return search(root->right, target);
}
对于树的指针节点,那么不能直接把节点赋值(不能直接root = tmpTree),只能把元素一一赋值。下面给出一个三叉树插入子树,进行搜索插入的例子(保证父节点已经存在)
// 在三叉树中搜索并插入某个值
void searchInsert(Tree* root, Tree* tmpTree) {
if (root == NULL) {
//千万别忘了递归时可能遇到NULL
return;
}
if (root->data == tmpTree->data) {
if (root->left == NULL) {
root->left = tmpTree->left;
}
if (root->mid == NULL) {
root->mid = tmpTree->mid;
}
if (root->right == NULL) {
root->right = tmpTree->right;
}
}
searchInsert(root->left, tmpTree);
searchInsert(root->mid, tmpTree);
searchInsert(root->right, tmpTree);
}
二叉树的拷贝,删除,高度
用的不太多,了解一下。
二叉查找树
非常重要,必考内容,也是最基本的内容。
定义
二叉查找树或者为空二叉树, 或者为具有以下性质的二叉树:
- 若根结点的左子树不空, 则左子树上所有结点的值都小于根结点的值;
- 若根结点的右子树不空, 则右子树上所有结点的值都大于或等于根结点的值。
每一课子树也分别是二叉查找树。
理想情况下查找效率为O(log2n).
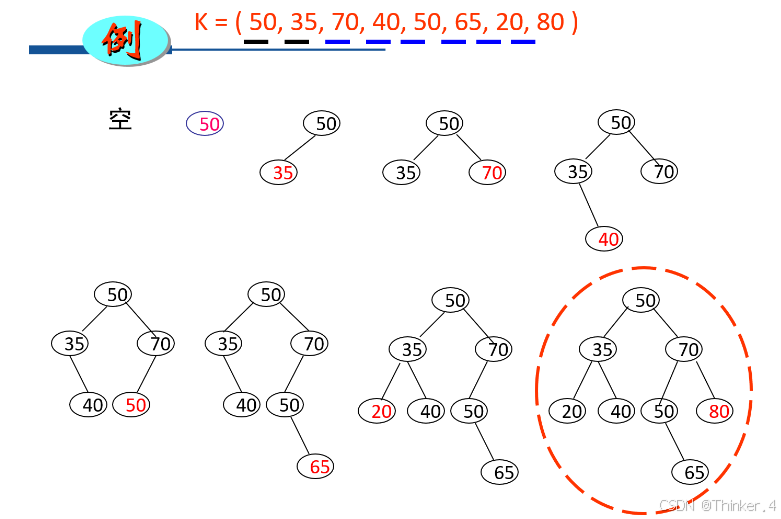
构建
设K=( k1, k2, k3, … , kn )为具有n个数据元素的序列。从序列的第一个元素开始,依次取序列中的元素,每取一个元素ki,按照下述原则将ki 插入到二叉树中:
- 若二叉树为空, 则ki 作为该二叉树的根结点。
- 若二叉树非空, 则将ki 与该二叉树的根结点的值进行比较, 若ki 小于根结点的值,则将ki插入到根结点的左子树中;否则,将ki 插入到根结点的右子树中。
将ki 插入到左子树或者右子树中仍然遵循上述原则(递归)。
插入代码
我们避免使用递归,便于理解。注意头文件、全局变量。
Tree* Root = NULL; //作为全局变量,是二叉查找树的根
void insertBST(Datatype item){
//建立新节点
Tree* p, * q;
p = (Tree*)malloc(sizeof(Tree));
p->data = item;
p->left = NULL;
p->right = NULL;
if (Root == NULL) {
Root = p;
}
else {
q = Root;
while (1) {
//比较值的大小,小的向左,大的向右
if (item < q->data) {
if (q->left == NULL) {
q->left = p;
break;
}
else {
q = q->left;
}
}
else if (item > q->data) {
if (q->right == NULL) {
q->right = p;
break;
}
else {
q = q->right;
}
}
else {
//树中有该元素
//根据具体情况处理
break;
}
}
}
}
void sortTree(Datatype k[], int n)
{
int i;
for (i = 0; i < n; i++) {
insertBST(k[i]);
}
}
删除的话具体问题具体分析。一般使用懒惰删除。
查找代码
查找过程很简单:
同样我们采用非递归算法:
Tree* searchBST(Tree* t, Datatype key) {
Tree* p = t;
while (p) {
if (key == p->data) {
return p;
}
else if (key > p->data) {
p = p->right;
}
else {
p = p->left;
}
}
return NULL;
}
searchBST(Root, key);
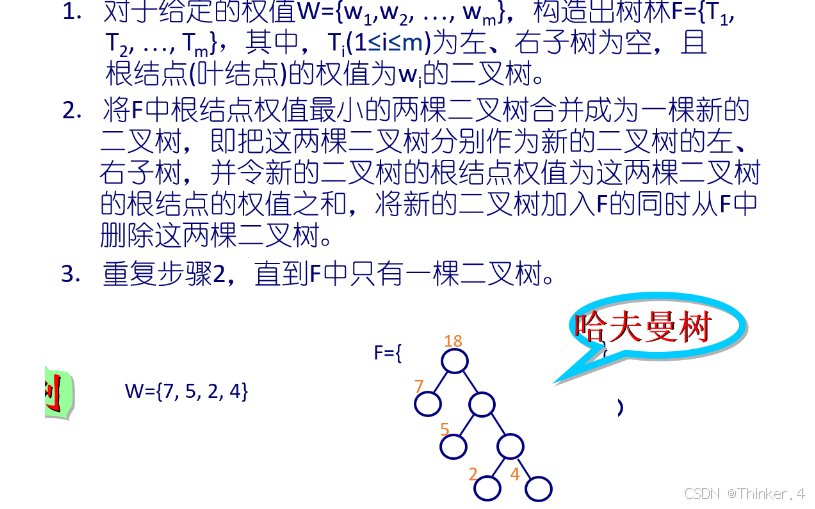
哈夫曼树
定义与特点
是一种带权树。给定一组权值,构造出的具有最小带权路径长度的二叉树称为哈夫曼树。
有以下重要特征:
- 权值越大的叶结点离根结点越近,权值越小的叶结点离根结点越远;
- 无度为1的结点。(最重要特征)
- 哈夫曼树不唯一。
构造思想
应用-哈夫曼编码
哈夫曼编码是最短编码。具体实践,这是实验课的要求。
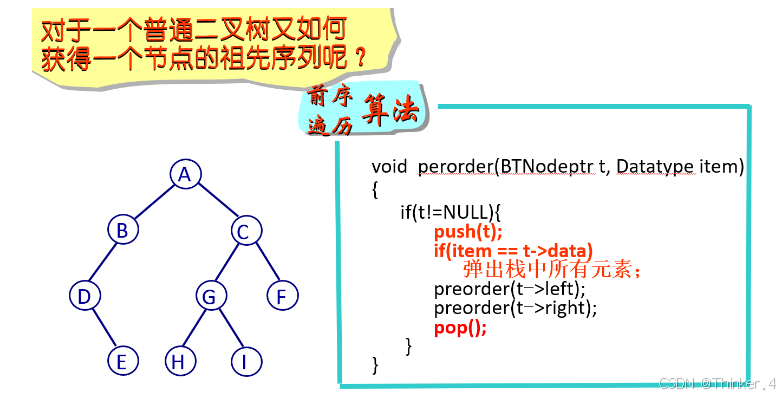
应用1-输出路径
如何输出一棵二叉树中从根节点到某节点的路径?
我们在应用四中详细介绍一些更好的方案。
应用2-服务优化
BUAA的一个作业题。更多作业题在应用7-9中展示。
【问题描述】
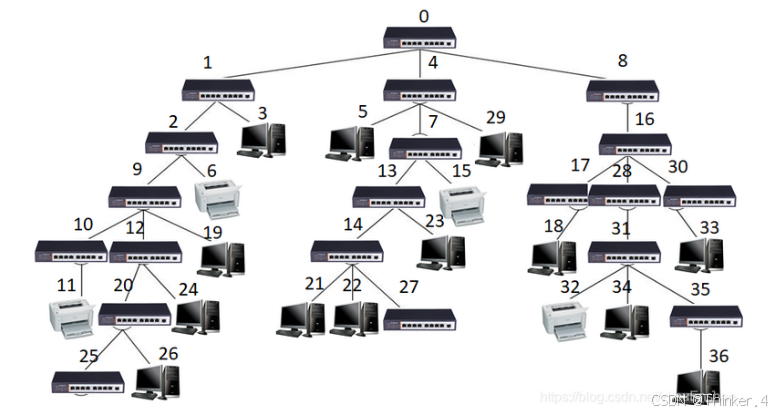
假设某机场所有登机⼝(Gate)呈树形排列(树的度为3),安检处为树的根,如下图所示。图中的分叉结点(编号⼤于等于100)表示分叉路⼝,登机⼝⽤⼩于100的编号表示(其⼀定是⼀个叶结点)。通过对机场所有出发航班的⽇志分析,得知每个登机⼝每天的平均发送旅客流量。作为提升机场服务⽔平的⼀个措施,在不改变所有航班相对关系的情况下(即:出发时间不变,原在同⼀登机⼝的航班不变),仅改变登机⼝(例如:将3号登机⼝改到5号登机⼝的位置),使得整体旅客到登机⼝的时间有所减少(即:从安检⼝到登机⼝所经过的分叉路⼝最少)。
编写程序模拟上述登机⼝的调整,登机⼝调整规则如下:
1)⾸先按照由⼤到⼩的顺序对输⼊的登机⼝流量进⾏排序,流量相同的按照登机⼝编号由⼩到⼤排序;
2)从上述登机⼝树的树根开始,将登机⼝按照从上到下(安检⼝在最上⽅)、从左到右的顺序,依次对应上⾯排序后将要调整的登机⼝。
例如上图的树中,若只考虑登机⼝,则从上到下有三层,第⼀层从左到右的顺序为:5、6、14、13,第⼆层从左到右的顺序为:7、8、9、10、1、2、18、17、16、15,第三层从左到右的顺序为:11、12、3、4、20、19。若按规则1排序后流量由⼤⾄⼩的前五个登机⼝为3、12、16、20、15,则将流量最⼤的3号登机⼝调整到最上层且最左边的位置(即:5号登机⼝的位置),12号调整到6号,16号调整到14号,20号调整到13号,15号调整到第⼆层最左边的位置(即7号登机⼝的位置)。
【输⼊形式】
1)⾸先按层次从根开始依次输⼊树结点之间的关系。其中分叉结点编号从数字100开始(树根结点编号为100,其它分叉结点编号没 有规律但不会重复),登机⼝为编号⼩于100的数字(编号没有规律但不会重复,其⼀定是⼀个叶结点)。树中结点间关系⽤下⾯⽅式描述:
R S1 S2 S3 -1
其中R为分叉结点,从左⾄右S1,S2,S3分别为树叉R的⼦结点,其可为树叉或登机⼝,由于树的度为3,S1,S2,S3中⾄多可以2个为空,最后该⾏以-1和换⾏符结束。各项间以⼀个空格分隔。如:
100 101 102 103 -1
表明编号100的树根有三个⼦叉,编号分别为101、102和103,⼜如:
104 7 8 -1
表明树叉104上有2个编号分别为7和8的登机⼝。
假设分叉结点数不超过100个。分叉结点输⼊的顺序不确定,但可以确定:输⼊某个分叉结点信息时,其⽗结点的信息已经输⼊。
输⼊完所有树结点关系后,在新的⼀⾏上输⼊-1表示树结点关系输⼊完毕。
2)接下来输⼊登机⼝的流量信息,每个登机⼝流量信息分占⼀⾏,分别包括登机⼝编号(1~99之间的整数)和流量(⼤于0的整数),两整数间以⼀个空格分隔。登机⼝数⽬与前⾯构造树时的登机机⼝数⽬⼀致。
【输出形式】
按照上述调整规则中排序后的顺序(即按旅客流量由⼤到⼩,流量相同的按照登机⼝编号由⼩到⼤)依次分⾏输出每个登机⼝的调整结果:先输出调整前的登机⼝编号,然后输出字符串"->"(由英⽂减号字符与英⽂⼤于字符组成),再输出要调整到的登机⼝编号。
【样例输⼊】
100 101 102 103 -1
103 14 108 13 -1
101 5 104 6 -1
104 7 8 -1
102 105 106 107 -1
106 1 110 2 -1
108 16 15 -1
107 18 111 17 -1
110 3 4 -1
105 9 109 10 -1
111 20 19 -1
109 11 12 -1
-1
17 865
5 668
20 3000
13 1020
11 980
8 2202
15 1897
6 1001
14 922
7 2178
19 2189
1 1267
12 3281
2 980
18 1020
10 980
3 1876
9 1197
16 980
4 576
【样例输出】
12->5
20->6
8->14
19->13
7->7
15->8
3->9
1->10
9->1
13->2
18->18
6->17
2->16
10->15
11->11
16->12
14->3
17->4
5->20
4->19
【样例说明】
样例输⼊了12条树结点关系,形成了如上图的树。然后输⼊了20个登机⼝的流量,将这20个登机⼝按照上述调整规则1排序后形成的顺序为:12、20、8、19、7、15、3、1、9、13、18、6、2、10、11、16、14、17、5、4。最后按该顺序将所有登机⼝按照上述调整规则2进⾏调整,输出调整结果。
//完整代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct _tree {
int data;
struct _tree* left, * mid, * right;
}Tree;
typedef struct _gate {
int gate;
int num;
}Gate;
Tree* T;
Tree* Q[100];
int front, rear;
int gate[100]; //所有登机口序号,按照层次遍历
int cntGate;
Gate orderGate[100];
Tree* createNode(int data);
void searchInsert(Tree* root, Tree* tmpTree);
void input();
void InitQueue(Tree* Q[]);
void EnQueue(Tree* Q[], Tree* T);
Tree* DeQueue(Tree* Q[]);
int isEmpty(Tree* Q[]);
void LevelOrderTraverse(Tree* T);
int cmp(const void* a, const void* b);
void createGate();
int main()
{
input();
LevelOrderTraverse(T);
createGate();
return 0;
}
Tree* createNode(int data) {
Tree* newNode = (Tree*)malloc(sizeof(Tree));
if (newNode != NULL) {
newNode->data = data;
newNode->left = newNode->mid = newNode->right = NULL;
}
return newNode;
}
// 在三叉树中搜索某个值
void searchInsert(Tree* root, Tree* tmpTree) {
if (root == NULL) {
return;
}
if (root->data == tmpTree->data) {
if (root->left == NULL) {
root->left = tmpTree->left;
}
if (root->mid == NULL) {
root->mid = tmpTree->mid;
}
if (root->right == NULL) {
root->right = tmpTree->right;
}
}
searchInsert(root->left, tmpTree);
searchInsert(root->mid, tmpTree);
searchInsert(root->right, tmpTree);
}
void input() {
int i, j;
int n1, n2, n3, n4;
Tree* tmpTree;
Tree* t1, * t2, * t3;
while (1) {
scanf("%d", &n1);
if (n1 == -1) {
break;
}
else {
scanf("%d%d", &n2, &n3);
if (n3 > 100) {
//内部分支
scanf("%d", &n4);
tmpTree = (Tree*)malloc(sizeof(Tree));
t1 = createNode(n2);
t2 = createNode(n3);
t3 = createNode(n4);
tmpTree->data = n1;
tmpTree->left = t1;
tmpTree->mid = t2;
tmpTree->right = t3;
}
else {
//最头上分支
tmpTree = (Tree*)malloc(sizeof(Tree));
t1 = createNode(n2);
t2 = createNode(n3);
tmpTree->data = n1;
tmpTree->left = t1;
tmpTree->mid = NULL;
tmpTree->right = t2;
}
scanf("%d", &n1); //把-1吃掉
//搜索节点,插入树中
if (T == NULL) {
T = tmpTree;
}
else {
searchInsert(T, tmpTree);
free(tmpTree);
}
}
}
}
void InitQueue(Tree* Q[]) {
front = rear = 0;
}
void EnQueue(Tree* Q[], Tree* T) {
Q[rear++] = T;
}
Tree* DeQueue(Tree* Q[]) {
return Q[front++];
}
int isEmpty(Tree* Q[]) {
return front == rear;
}
void LevelOrderTraverse(Tree* T) {
InitQueue(Q); //初始化辅助队列
Tree* p;
EnQueue(Q, T); //将根节点入队
while (!isEmpty(Q)) { //队列不空则循环
p = DeQueue(Q); //队头结点出队
if (p->data < 100) {
//访问出队结点
//printf("%d ", p->data);
gate[cntGate++] = p->data;
}
if (p->left != NULL) {
EnQueue(Q, p->left); //左子树不空,则左子树根节点入队
}
if (p->mid != NULL) {
EnQueue(Q, p->mid); //中子树不空,则中子树根节点入队
}
if (p->right != NULL) {
EnQueue(Q, p->right); //右子树不空,则右子树根节点入队
}
}
}
int cmp(const void* a, const void* b) {
Gate g1 = *(Gate*)a;
Gate g2 = *(Gate*)b;
if (g1.num == g2.num) {
return g1.gate - g2.gate;
}
return g2.num - g1.num;
}
void createGate(){
int i;
for (i = 0; i < cntGate; i++) {
scanf("%d%d", &orderGate[i].gate, &orderGate[i].num);
}
qsort(orderGate, cntGate, sizeof(Gate), cmp);
for (i = 0; i < cntGate; i++) {
printf("%d->%d\n", orderGate[i].gate, gate[i]);
}
}
经典基本题。只要调用我们快速教程的封装函数,稍加修改就能快速通过。整体逻辑比较顺畅,就是输入数据,构造三叉树(另,这个给的输入个人感觉比较奇怪,-1不起作用,当然可能是个人理解有误),然后BFS层次遍历,然后又给了登机口的另一组指标——客流量,像个封装体,又想考排序。我们qsort直接搞定(见快速教程排序)。
btw,该机场图神似旧金山国际机场(SFO,KSFO),本人层到访过数次,对于留学生来说应该是经典回忆了。一个大安检门,安检门的对面是开了好几十年的Compass书店,真的巨回忆。本人7岁时曾居住美国,当时就对这个书店有印象。2024年寒假本人赴美有事,相隔十多年再次来到旧金山机场,这个书店仍然在安检门的正对面。
旧金山四条垂直跑道,我永远忘不了在28R跑道降落时能在左侧看到防波堤——旧金山机场的经典场景。在这里,你可以看到全世界最著名的SFO平行起降。以及美国国内最垃圾的美联航,在飞国际航班时总能给我小温暖。疫情后复航不就,本人有幸乘坐UA889,UA888往返旧金山,北京首都。是一段珍贵的回忆,尤其对于我这样的飞友。
言归正传,这个图很像旧金山机场航站楼:
应用3-文件拷贝
【问题描述】
假设已有一个文件目录和一组带有全目录路径的文件,请将该组文件按下面规则拷贝到已有文件目录中,并按要求输出拷贝后的文件目录:
1.若相应目录下无给定文件,则将该文件直接拷贝到相应目录下;
2.若相应目录下有给定同名文件且拷入文件比原有文件日期较新,则用新文件覆盖已有同名文件,否则不执行任何操作;
3.若相应目录中无给定文件目录路径上的某个子目录,则在当前目录相应目录下创建相应子目录及文件。
假设要拷贝的文件根目录与已有文件根目录是相同的。
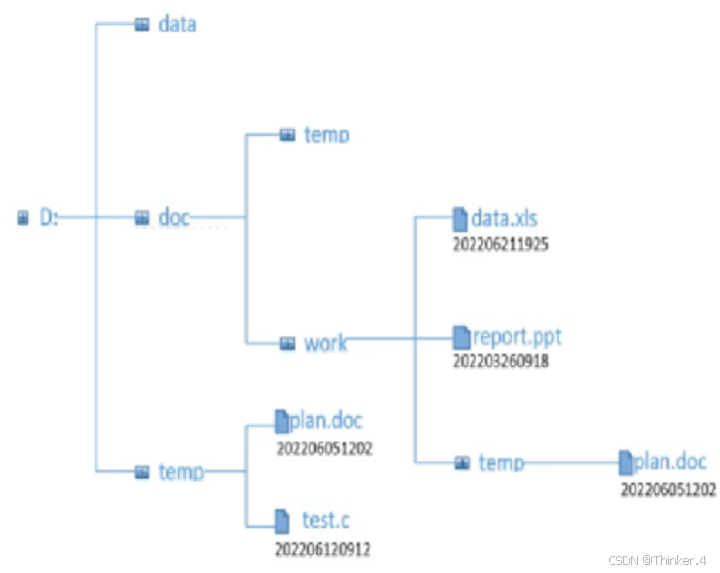
例如:若已有下图所示目录(文件名下方数字是其日期时间):
要拷贝的一组文件(文件名后为相应文件日期时间)如下所示:
D:\doc\test\test.c 202205181107
D:\doc\work\data.xls 202206230907
D:\doc\work\temp\plans.doc 202206171705
D:\temp\plan.doc 202206171502
D:\doc\work\report.ppt 202203250830
D:\doc\work\math.doc 202207021506
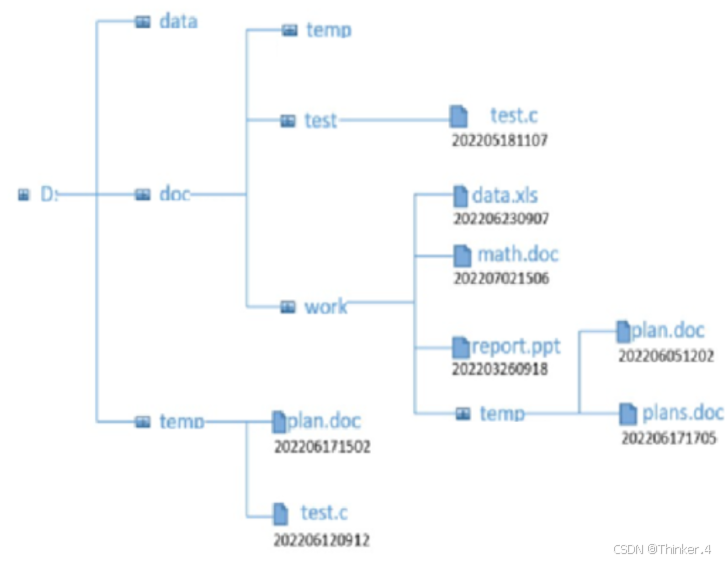
按上面规则文件拷贝后目录如下图所示:
【输入形式】
目录以下面形式给出:a1(a11,a12,a13,……,a1n),表中a1是根目录编号,括号中每个元素,可以是一个具体文件编号 ,也可以是以同样方式定义的一个子目录编号。例如,下面方式:1(2(4),3(5(7,8,9),6))则表示了如下目录树:
其中1为根结点目录编号,其有2个编号为2和3的子目录,而编号为2的子目录有一个编号为4的子目录或文件,以此类推。任一结点的子结点个数不超过100个。所有编号大于等于1且小于等于1000,编号在一个目录树中是惟一的。
以上面形式定义的一个已有目录树保存在当前目录下的文件in.txt中,目录树中的字符都是英文字符,字符数不超过5000,只包含数字、小括号和逗号;在目录树后,in.txt分行保存目录树中每个结点编号所对应的文件名(不超过20个字符)、文件属性(1表示目录,0表示普通文件)和日期时间(文件用12位数字串表示,目录没有时间,用英文减号字符"-"表示),各数据间以1个空格分隔。
从标准输入读入要拷贝的文件数目,然后分行读入每个文件的全路径信息和日期时间(两者之间以一个空格分隔),最后一个文件信息后也有换行符。
【输出形式】
按层次遍历序分行输出拷贝后目录树中的文件及相应日期时间,同一层的按时间序输出,若同一层的时间也相同,则按照文件名的字典序输出。注意只输出普通文件信息,不输出目录信息。
【样例输入】
in.txt文件内容如下:
100(25,32(18,1(26,37,66(17))),101(2,3))
100 D: 1 -
101 temp 1 -
2 plan.doc 0 202206051202
3 test.c 0 202206120912
25 data 1 -
32 doc 1 -
18 temp 1 -
1 work 1 -
26 data.xls 0 202206211925
37 report.ppt 0 202203260918
66 temp 1 -
17 plan.doc 0 202206051202
标准输入如下:
6
D:\doc\test\test.c 202205181107
D:\doc\work\data.xls 202206230907
D:\doc\work\temp\plans.doc 202206171705
D:\temp\plan.doc 202206171502
D:\doc\work\report.ppt 202203250830
D:\doc\work\math.doc 202207021506
【样例输出】
test.c 202206120912
plan.doc 202206171502
report.ppt 202203260918
test.c 202205181107
data.xls 202206230907
math.doc 202207021506
plan.doc 202206051202
plans.doc 202206171705
【样例说明】
根据in.txt文件中输入的目录树和文件目录信息,可以生成如上面第一张图所示的文件目录;将标准输入中读入的6个文件拷贝到该文件目录后,状态如上面第二张图所示,最后将其中的文件信息按层次输出到标准输出。
【评分标准】
该题要求将指定的文件拷贝到文件目录中,提交程序名为copy.c。
//完整代码示例
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
typedef struct _file {
char num[1001];
char name[50];
int charDigit; //属性,0或1
char time[20];
}File;
typedef struct _Tree {
File f;
struct _Tree* child[100]; //所有子树
int childCount; //字数数量
}Tree;
Tree* T;
char OriTree[5000]; //文件中的第一行,原始数据
int index; //文件中的索引,记录OriTree读到的位置
int cntFile; //文件中已有的文件数量
int cntAdd; //要添加的文件数
Tree* Q[100]; //层次遍历
int front, rear;
void readIn();
Tree* createTree();
void searchInsert(Tree* root, File f);
void copyToTree(char path[], char addTime[]);
void LevelOrderTraverse();
void EnQueue(Tree* T);
Tree* DeQueue();
int isEmpty(Tree* Q[]);
int cmp(const void* a, const void* b);
int main()
{
readIn();
LevelOrderTraverse();
return 0;
}
void readIn() {
FILE* fp = fopen("in.txt", "r");
File f;
int i;
char path[2000]; //要拷贝的路径
char addTime[20]; //要拷贝的时间
fscanf(fp, "%s", OriTree);
T = createTree();
for (i = 0; i < cntFile; i++) {
fscanf(fp, "%s %s %d %s", f.num, f.name, &f.charDigit, f.time);
searchInsert(T, f);
}
fclose(fp);
scanf("%d", &cntAdd);
for (i = 0; i < cntAdd; i++) {
scanf("%s %s", path, addTime);
copyToTree(path, addTime);
}
}
Tree* createTree() {
Tree* node = (Tree*)malloc(sizeof(Tree));
node->childCount = 0;
int numIndex = 0;
//读取目录编号
while (isdigit(OriTree[index])) {
node->f.num[numIndex++] = OriTree[index++];
}
node->f.num[numIndex] = '\0';
cntFile++;
//如果遇到左括号,说明有孩子节点
if (OriTree[index] == '(') {
index++;
while (OriTree[index] != ')') {
node->child[node->childCount++] = createTree();
if (OriTree[index] == ',') {
index++;
}
}
index++;
}
return node;
}
void searchInsert(Tree* root, File f) {
if (root == NULL) {
//千万别忘了递归时可能遇到NULL
return;
}
if (strcmp(root->f.num, f.num) == 0) {
strcpy(root->f.name, f.name);
root->f.charDigit = f.charDigit;
strcpy(root->f.time, f.time);
}
for (int i = 0; i < root->childCount; i++) {
searchInsert(root->child[i], f);
}
}
void copyToTree(char path[], char addTime[]) {
int i;
//分割路径并插入到树中
char* token = strtok(path, "\\");
token = strtok(NULL, "\\"); //把D:过滤掉
Tree* current = T;
while (token != NULL) {
int found = 0;
//先搜索
for (i = 0; i < current->childCount; i++) {
if (strcmp(current->child[i]->f.name, token) == 0) {
current = current->child[i];
found = 1;
if (strstr(token, ".")) {
if (strcmp(current->f.time, addTime) < 0) {
strcpy(current->f.time, addTime);
}
}
break;
}
}
if (!found) {
//建立新结点
Tree* newNode = (Tree*)malloc(sizeof(Tree));
strcpy(newNode->f.name, token);
newNode->childCount = 0;
if (strstr(token, ".")) {
strcpy(newNode->f.time, addTime);
}
else {
strcpy(newNode->f.time, "-");
}
//插入树中,指针直接指向新节点
current->child[current->childCount++] = newNode;
current = newNode;
}
token = strtok(NULL, "\\");
}
}
void EnQueue(Tree* T) {
Q[rear++] = T;
}
Tree* DeQueue() {
return Q[front++];
}
int isEmpty(Tree* Q[]) {
return front == rear;
}
void LevelOrderTraverse() {
int i;
Tree* p;
Tree* level[1000];
int levelCount;
EnQueue(T); //将根节点入队
while (!isEmpty(Q)) { //队列不空则循环
int levelSize = rear - front; //当前层的节点数
levelCount = 0;
//提取当前层的所有节点
for (i = 0; i < levelSize; i++) {
p = DeQueue();
level[levelCount++] = p;
//将下一层的所有节点入队
for (int j = 0; j < p->childCount; j++) {
EnQueue(p->child[j]);
}
}
// 对当前层的子节点进行排序
qsort(level, levelCount, sizeof(Tree*), cmp);
//输出当前层的所有节点
for (int i = 0; i < levelCount; i++) {
if (strcmp(level[i]->f.time, "-") != 0) {
printf("%s %s\n", level[i]->f.name, level[i]->f.time);
}
}
}
}
int cmp(const void* a, const void* b) {
Tree* t1 = *(Tree**)a;
Tree* t2 = *(Tree**)b;
if (strcmp(t1->f.time, t2->f.time) == 0) {
return strcmp(t1->f.name, t2->f.name);
}
return strcmp(t1->f.time, t2->f.time);
}
这道题是封装题,很多步骤都可以单独拆成一个题。比如括号形式构造树,就一定要会。
应用4-打印路径
应用一非常水地告诉了一种课件上的方法。
这里用一个基本题引入(2021BUAA数据结构期末),题目虽然简单,但是有一些值得学习的地方,尤其是输出路径:
二叉搜索树
【问题描述】
编写程序读入一组整数,按输入顺序构造一棵二叉查找树(BST树)来查找并统计相应整数的出现次 数,BST树的构造规则如下:
- 在输入整数过程中按照左子结点值小于根结点值、右子结点值大于根结点值的方式构造一棵BST树;
- 输入的整数等于BST树中某结点值时,该结点的出现次数加1。
示例详见下面的样例。 对于最终构建的BST树,要求统计如下数据:
- 在BST树的创建及查找整数过程中总的比较次数,仅统计输入的整数与结点值进行比较的次数,不统计指针的判断次数;
- 出现次数最多的整数的比较路径;比较路径是指BST树中从根结点到该节点的路径;若出现次数最多 的整数有多个,则只输出按照前序遍历次序访问的第一个出现次数最多的整数的比较路径。
【输入形式】
先从控制台输入整数的个数n(大于等于1),然后在下一行输入n个整数,以一个空格分隔各个整数。
【输出形式】
先向控制台输出在BST树的创建及查找整数过程中总的比较次数,然后在下一行输出按照前序遍历次序 访问的第一个出现次数最多的整数的比较路径,用该路径上各结点对应的整数表示,各整数间以一个空 格分隔,最后一个整数后有无空格均可。
【样例输入】
12
670 1360 1871 921 128 1871 57 -200 1003 552 -200 57
【样例输出】
26
670 128 57
【样例说明】
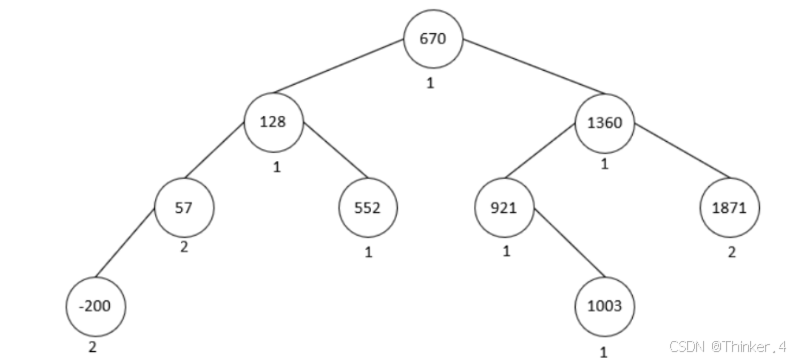
输入了12个整数,根据上述构造规则,建立的BST树如下图所示:
其中结点中的值为输入的整数值,结点下方的数值为该整数出现的次数。 开始BST树为空,第一个整数670作为根结点,没有与结点值进行比较,比较次数为0;第二个整数1360 与结点670比较了1次;第三个整数1871与结点670和结点1360各比较了1次;第六个整数1871与结点 670、1360和1871各比较了1次;其它整数与上述整数类同;在该BST树的创建及查找整数过程中总的比 较次数为26次。 在该BST树中,出现次数最多的整数有三个,分别为1871、57和-200,其中按照前序遍历次序访问到的 第一个为57,所以要输出结点57的比较路径,即从根结点670到结点57的路径。
//完整代码-示例一
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct _Tree {
int digit;
int cnt;
struct _Tree* left, * right, *parent;
}Tree;
Tree* T;
int cmpCnt; //比较次数
int max = 1;//出现次数最多的整数的出现次数
int index; //总的整数个数
int path[100];
int cntPath;
void insertBST(int item) {
//建立新节点
Tree* p, * q;
p = (Tree*)malloc(sizeof(Tree));
p->digit = item;
p->left = NULL;
p->right = NULL;
p->parent = NULL;
if (T == NULL) {
T = p;
}
else {
q = T;
while (1) {
//比较值的大小,小的向左,大的向右
cmpCnt++;
if (item < q->digit) {
if (q->left == NULL) {
p->cnt = 1;
q->left = p;
p->parent = q;
break;
}
else {
q = q->left;
}
}
else if (item > q->digit) {
if (q->right == NULL) {
p->cnt = 1;
q->right = p;
p->parent = q;
break;
}
else {
q = q->right;
}
}
else {
q->cnt++;
if (max < q->cnt) {
max = q->cnt;
}
break;
}
}
}
}
Tree* PreOrderTraverse(Tree* t) {
if (t != NULL) {
if (t->cnt == max) {
return t;
}
Tree* leftResult = PreOrderTraverse(t->left);
if (leftResult != NULL) {
return leftResult;
}
Tree* rightResult = PreOrderTraverse(t->right);
if (rightResult != NULL) {
return rightResult;
}
}
return NULL;
}
void printPath() {
Tree* target = PreOrderTraverse(T);
while (target != NULL) {
path[cntPath++] = target->digit;
target = target->parent;
}
cntPath--;
while (cntPath >= 0) {
printf("%d ", path[cntPath--]);
}
}
void input() {
int num;
scanf("%d", &index);
for (int i = 0; i < index; i++) {
scanf("%d", &num);
insertBST(num);
}
printf("%d\n", cmpCnt);
}
int main()
{
input();
printPath();
return 0;
}
这道题主要介绍三叉链表。除了左右孩子节点,还要有指向父亲节点的指针。因为,**要输出路径,所以我们用三叉链表来避免复杂的回溯算法。**这样,就可以顺藤摸瓜的一路找到根节点,从而输出路径。
采用基本做法,也就是中断遍历的方法一。printPath时通过构造一个数组来实现反向输出。整体比较通俗易懂。我们重点介绍方法二:
//完整代码-示例2
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct _Tree {
int digit;
int cnt;
struct _Tree* left, * right, *parent;
}Tree;
Tree* T;
int cmpCnt; //比较次数
int max = 1;//出现次数最多的整数的出现次数
int index; //总的整数个数
int path[100];
int cntPath;
Tree* target;
int flag;
void insertBST(int item) {
//建立新节点
Tree* p, * q;
p = (Tree*)malloc(sizeof(Tree));
p->digit = item;
p->left = NULL;
p->right = NULL;
p->parent = NULL;
if (T == NULL) {
T = p;
}
else {
q = T;
while (1) {
//比较值的大小,小的向左,大的向右
cmpCnt++;
if (item < q->digit) {
if (q->left == NULL) {
p->cnt = 1;
q->left = p;
p->parent = q;
break;
}
else {
q = q->left;
}
}
else if (item > q->digit) {
if (q->right == NULL) {
p->cnt = 1;
q->right = p;
p->parent = q;
break;
}
else {
q = q->right;
}
}
else {
q->cnt++;
if (max < q->cnt) {
max = q->cnt;
}
break;
}
}
}
}
void PreOrderTraverse(Tree* t) {
if (!flag && t != NULL) {
if (t->cnt == max) {
flag = 1;
target = t;
}
PreOrderTraverse(t->left);
PreOrderTraverse(t->right);
}
}
void printPath(Tree* target) {
if (target == NULL) {
return;
}
printPath(target->parent);
printf("%d ", target->digit);
}
void input() {
int num;
scanf("%d", &index);
for (int i = 0; i < index; i++) {
scanf("%d", &num);
insertBST(num);
}
printf("%d\n", cmpCnt);
}
int main()
{
input();
PreOrderTraverse(T);
printPath(target);
return 0;
}
也就是中断遍历的方法二。这里重点推荐printpath中的递归写法。这种方法和方法一的本质区别就是,不在printpath中调用遍历函数,而是直接在main函数中进行调用。**重点推荐通过递归而避免反向数组(栈),一步到位输出 。**图中也有类似的问题。
应用5-表达式树
首先我们来看一个基本的需求:后缀表达式转中缀表达式。
后缀转中缀
该转化的难点在于如何添加括号。基本思路为先把后缀表达式转化为表达式树,再进行中序遍历。
数字版
输入的是数字,数字以及运算符之间都用一个空格区分。例如:后缀表达式为235+*71/+4-,转化为中缀为2*(3+5)+7/1-4。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <stdlib.h>
typedef struct Node {
int num;
char op;
struct Node* left, * right, * leftpa, * rightpa;
} Tree; // 子节点与祖先节点都需要存储,若 a 为 b 的左节点,则 b 为 a 的右祖先
Tree* numjudge;
char temp[20] = { 0 };
Tree* createNode(char op, int num) {
Tree* node = (Tree*)malloc(sizeof(Tree));
node->op = op;
node->num = num;
node->left = node->right = node->leftpa = node->rightpa = NULL;
return node;
}
Tree* buildExpressionTree(char* postfix) {
Tree* stack[100];
int stackTop = -1;
int len = strlen(postfix);
for (int i = 0; i < len; i++) {
if (isspace(postfix[i])) continue;
if (isdigit(postfix[i])) {
int num = 0;
while (i < len && isdigit(postfix[i])) {
num = num * 10 + (postfix[i] - '0');
i++;
}
i--;
stack[++stackTop] = createNode('\0', num);
} else {
Tree* node = createNode(postfix[i], 0);
node->right = stack[stackTop--];
node->left = stack[stackTop--];
stack[++stackTop] = node;
if (node->left != NULL) {
node->left->rightpa = node;
}
if (node->right != NULL) {
node->right->leftpa = node;
}
}
}
return stack[0];
}
void middle_order(Tree* t) {
memset(temp, 0, sizeof(temp));
if (t != NULL) {
middle_order(t->left);
if (t->op != '\0') {
if (t->op == '*' || t->op == '/') {
if (t->left->op != '\0') {
if (t->left->op == '+' || t->left->op == '-')
printf(")");
}
}
printf("%c", t->op);
if (t->op == '*' || t->op == '/') {
if (t->right->op != '\0') {
printf("(");
}
}
} else {
if (t->rightpa != NULL) {
numjudge = t->rightpa;
while (numjudge->rightpa != NULL) {
if (numjudge->rightpa->op == '*' || numjudge->rightpa->op == '/')
{
if (numjudge->op == '+' || numjudge->op == '-')
printf("(");
}
numjudge = numjudge->rightpa;
}
}
printf("%d", t->num);
if (t->leftpa != NULL) {
numjudge = t->leftpa;
while (numjudge->leftpa != NULL) {
if (numjudge->leftpa->op == '*' || numjudge->leftpa->op == '/')
printf(")");
numjudge = numjudge->leftpa;
}
}
}
middle_order(t->right);
}
}
int main() {
char postfix[] = "2 3 5 + * 7 1 / + 4 -";
Tree* root = buildExpressionTree(postfix);
middle_order(root);
return 0;
}
字母版
例如输入后缀表达式a b c *+d e * f + g / +,给出中缀表达式为a+b*c+(d*e+f)/g。输入时用空格表示分割。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <stdlib.h>
typedef struct Node {
char num; // 修改为 char 类型
char op;
struct Node* left, * right, * leftpa, * rightpa;
} Tree; // 子节点与祖先节点都需要存储,若 a 为 b 的左节点,则 b 为 a 的右祖先
Tree* numjudge;
char temp[20] = { 0 };
Tree* createNode(char op, char num) { // 修改 num 类型为 char
Tree* node = (Tree*)malloc(sizeof(Tree));
node->op = op;
node->num = num;
node->left = node->right = node->leftpa = node->rightpa = NULL;
return node;
}
Tree* buildExpressionTree(char* postfix) {
Tree* stack[100];
int stackTop = -1;
int len = strlen(postfix);
for (int i = 0; i < len; i++) {
if (isspace(postfix[i])) continue;
if (isalpha(postfix[i])) { // 处理操作数,包括字母和数字
stack[++stackTop] = createNode('\0', postfix[i]);
}
else { // 处理运算符
Tree* node = createNode(postfix[i], '\0');
node->right = stack[stackTop--];
node->left = stack[stackTop--];
stack[++stackTop] = node;
if (node->left != NULL) {
node->left->rightpa = node;
}
if (node->right != NULL) {
node->right->leftpa = node;
}
}
}
return stack[0];
}
void middle_order(Tree* t) {
if (t != NULL) {
if (t->op == '*' || t->op == '/') {
if (t->left != NULL && (t->left->op == '+' || t->left->op == '-')) {
printf("(");
middle_order(t->left);
printf(")");
} else {
middle_order(t->left);
}
printf("%c", t->op);
if (t->right != NULL && (t->right->op == '+' || t->right->op == '-')) {
printf("(");
middle_order(t->right);
printf(")");
} else {
middle_order(t->right);
}
} else {
middle_order(t->left);
if (t->op != '\0') {
printf("%c", t->op);
} else {
printf("%c", t->num);
}
middle_order(t->right);
}
}
}
int main() {
char postfix[] = "a b c * + d e * f + g / +";
Tree* root = buildExpressionTree(postfix);
middle_order(root);
return 0;
}
计算表达式树
为了计算表达式树,我们需要对树进行后序遍历,并在每个运算符节点上执行相应的操作。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <stdlib.h>
typedef struct Node {
char num;
char op;
struct Node* left, * right, * parent;
} Tree;
Tree* createNode(char op, char num) {
Tree* node = (Tree*)malloc(sizeof(Tree));
node->op = op;
node->num = num;
node->left = node->right = node->parent = NULL;
return node;
}
Tree* buildExpressionTree(char* postfix) {
Tree* stack[100];
int stackTop = -1;
int len = strlen(postfix);
for (int i = 0; i < len; i++) {
if (isspace(postfix[i])) continue;
if (isalnum(postfix[i])) {
stack[++stackTop] = createNode('\0', postfix[i]);
} else {
Tree* node = createNode(postfix[i], '\0');
node->right = stack[stackTop--];
node->left = stack[stackTop--];
stack[++stackTop] = node;
if (node->left != NULL) {
node->left->parent = node;
}
if (node->right != NULL) {
node->right->parent = node;
}
}
}
return stack[0];
}
void middle_order(Tree* t) {
if (t != NULL) {
if (t->op == '*' || t->op == '/') {
if (t->left != NULL && (t->left->op == '+' || t->left->op == '-')) {
printf("(");
middle_order(t->left);
printf(")");
} else {
middle_order(t->left);
}
printf("%c", t->op);
if (t->right != NULL && (t->right->op == '+' || t->right->op == '-')) {
printf("(");
middle_order(t->right);
printf(")");
} else {
middle_order(t->right);
}
} else {
middle_order(t->left);
if (t->op != '\0') {
printf("%c", t->op);
} else {
printf("%c", t->num);
}
middle_order(t->right);
}
}
}
int evaluate(Tree* t) {
if (t == NULL) return 0;
if (t->op == '\0') {
return t->num - '0';
}
int leftVal = evaluate(t->left);
int rightVal = evaluate(t->right);
switch (t->op) {
case '+': return leftVal + rightVal;
case '-': return leftVal - rightVal;
case '*': return leftVal * rightVal;
case '/': return leftVal / rightVal;
}
return 0;
}
int main() {
char postfix[] = "2 3 5 * + 4 1 / +";
Tree* root = buildExpressionTree(postfix);
middle_order(root);
printf("\nResult: %d\n", evaluate(root));
return 0;
}
应用6-网络打印机选择
这是一个很变态的题目:
问题描述
某单位信息网络结构呈树型结构,网络中节点可为交换机、计算机和打印机三种设备,计算机和打印机只能位于树的叶节点上。如要从一台计算机上打印文档,请为它选择最近(即经过交换机最少)的打印机。
在该网络结构中,根交换机编号为0,其它设备编号可为任意有效正整数,每个交换机有8个端口(编号0-7)。当存在多个满足条件的打印机时,选择按树前序遍历序排在前面的打印机。
输入形式
首先从标准输入中输入两个整数,第一个整数表示当前网络中设备数目,第二个整数表示需要打印文档的计算机编号。两整数间以一个空格分隔。假设设备总数目不会超过300。
然后从当前目录下的in.txt读入相应设备配置表,该表每一行构成一个设备的属性,格式如下:
<设备ID> <类型> <设备父节点ID> <端口号>
<设备ID>为一个非负整数,表示设备编号;<类型>分为:0表示交换机、1表示计算机、2表示打印机;<设备父结点ID>为相应结点父结点编号,为一个有效非负整数;<端口号>为相应设备在父结点交换机中所处的端口编号,分别为0-7。由于设备配置表是按设备加入网络时的次序编排的,因此,表中第一行一定为根交换机(其属性为0 0 -1 -1);其它每个设备结点一定在其父设备结点之后输入。每行中设备属性间由一个空格分隔,最后一个属性后有换行符。
输出形式
向控制台输出所选择的打印机编号,及所经过的交换机的编号,顺序是从需要打印文档的计算机开始,编号间以一个空格分隔。
样例输入
37 19
in.txt中的信息如下:
0 0 -1 -1
1 0 0 0
2 0 1 2
3 1 1 5
4 0 0 1
5 1 4 0
6 2 2 2
7 0 4 2
8 0 0 4
9 0 2 0
10 0 9 0
11 2 10 3
12 0 9 2
13 0 7 0
14 0 13 0
15 2 7 3
16 0 8 1
17 0 16 0
18 1 17 5
19 1 9 5
20 0 12 1
21 1 14 1
22 1 14 2
23 1 13 2
24 1 12 5
25 0 20 1
26 1 20 2
27 0 14 7
28 0 16 1
29 1 4 3
30 0 16 7
31 0 28 0
32 2 31 0
33 1 30 2
34 1 31 2
35 0 31 5
36 1 35 3
样例输出
11 9 10
样例说明
样例输入中37表示当前网络共有37台设备,19表示编号为19的计算机要打印文档。in.txt设备表中第一行0 0 -1 -1表示根节点交换机设备,其设备编号为0 、设备类型为0(交换机)、父结点设备编号-1表示无父设备、端口-1表示无接入端口;设备表第二行1 0 0 0表示设备编号为1 、设备类型为0(交换机)、父结点设备编号0(根交换机)、端口0表示接入父结点端口0;设备表中行5 1 4 0表示设备编号为5 、设备类型为1(计算机)、父结点设备编号4、端口0表示接入4号交换机端口0;设备表中行6 2 2 2表示设备编号为6 、设备类型为2(打印机)、父结点设备编号2、端口2表示接入2号交换机端口2。
样例输出11 9 10表示选择设备编号为11的打印机打印文档,打印需要经过9号和10号交换机(尽管6号和11号打印机离19号计算机距离相同,但11号打印机按树前序遍历时排在6号之前)。
//参考代码(来源于网络)
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<stdlib.h>
#include<ctype.h>
#include<stdbool.h>
#define MAX 2000
typedef struct TreeNode { //简化的树形数组
int ID; //树节点的编号
int type; //树节点类型 (0表示交换机、1表示计算机、2表示打印机)
int parentID; //父结点编号
int portNumber; //父结点交换机中所处的端口编号,分别为0-7
struct TreeNode* child[9]; //树节点的子树地址8个端口(编号0-7) ************注意,至少要开 9,如果是 8可能会越界
}Tree, * Treep;
typedef struct queue { //前序遍历的存储队列
int ID; //树节点的编号
int type; //树节点类型
int parentID; //父结点编号
int portNumber; //父结点交换机中所处的端口编号
int when; //树节点第几次被访问 (前序遍历编号)
int pathNum; //一开始记录的是节点到根之间的距离,之后是计算机到打印机之间的距离
int path[200]; //记录节点到根之间的节点编号
int ancestor; //共同祖先
}queue;
Tree node[MAX]; //树形数组
queue q[MAX * 7], qq[MAX * 7], computer;//q是前序遍历构造的包含全部系统的队列,qq是前序遍历构造的含打印机和要求的计算机的队列,computer存储是要求计算机的内容
int i, j, n, head, target, printNum, top, ancestor, stack[300];//head是队头,target记录要求计算机的位置,printNum是打印机的总数,top是栈顶,ancestor是公共祖先,stack是栈
int ID, type, parentID, portNumber, computerID;//输入参数
void CreateTreeNode(FILE* fp); //构建树形数组
void SortTree(Treep root); //递归处理树形数组
void CreateQueue(Treep root); //前序遍历构造队列
int returnRoot(int ID, int pathNum); //返回根,同时记录途中信息
int findSameAncestor_and_calculatePath(int* a, int* b, int la, int lb);//找到公共祖先,同时记录两节点之间的距离
int cmp(const void* p1, const void* p2); //比较函数
int main()
{
FILE* fp = fopen("in.txt", "r");
scanf("%d %d", &n, &computerID);
CreateTreeNode(fp); //用树形数组模拟多叉树
SortTree(&node[0]); //递归处理树形数组
for (i = 0; i < head; i++) //构造qq, qq是前序遍历构造的含打印机和要求的计算机的队列
{
if (q[i].type == 2 || q[i].ID == computerID)
{
if (q[i].ID == computerID) target = printNum;//target记录要求计算机的位置
qq[printNum].ID = q[i].ID;
qq[printNum].type = q[i].type;
qq[printNum].parentID = q[i].parentID;
qq[printNum].portNumber = q[i].portNumber;
qq[printNum].when = q[i].when;
printNum++;
}
}
for (i = 0; i < printNum; i++)
{
top = 0;
qq[i].pathNum = returnRoot(qq[i].ID, 0); //计算 节点到根之间的距离,以及 记录节点到根之间的节点编号
}
computer.ID = computerID; //用computer拷贝target记录的信息
computer.type = qq[target].type;
computer.parentID = qq[target].parentID;
computer.portNumber = qq[target].portNumber;
computer.when = qq[target].when;
computer.pathNum = qq[target].pathNum;
memcpy(computer.path, qq[target].path, sizeof(qq[target].path)); //要用memcpy
for (i = 0; i < printNum; i++)
{
ancestor = 0;
qq[i].pathNum = findSameAncestor_and_calculatePath(qq[i].path, computer.path, qq[i].pathNum - 1, computer.pathNum - 1); //找到要求计算机和各个打印机的公共祖先,同时记录两者之间的距离
qq[i].ancestor = ancestor;
}
qq[target].pathNum = 0x3f3f3f3f; //一定不要忘了这一步操作,由于qq里还有计算机本身,如果不把其距离设为无穷大,不然距离最近的永远是它本身
qsort(qq, printNum, sizeof(queue), cmp);//排序
printf("%d ", qq[0].ID); //打印打印机编号
ID = node[computerID].parentID;
while (ID != qq[0].ancestor)
{
printf("%d ", ID); //输出计算机到公共祖先的节点ID
ID = node[ID].parentID;
}
printf("%d ", qq[0].ancestor);//输出公共祖先的节点ID
top = 0;
ID = qq[0].parentID;
while (ID != qq[0].ancestor)
{
stack[top] = ID; top++; //先存在栈里,等一下要倒着输出打印机到公共祖先的节点ID
ID = node[ID].parentID;
}
while (top--)
printf("%d ", stack[top]); //倒着输出打印机到公共祖先的节点ID
return 0;
}
int findSameAncestor_and_calculatePath(int* a, int* b, int la, int lb)
{
int times = 0, pathnum = 0, x, y;
for (x = 0; x < lb; x++) {
for (y = 0; y < la; y++) {
if (b[x] == a[y] && times == 0) { //由于公共祖先只有一个,所以靠times来判断
ancestor = a[y]; //记录公共祖先
pathnum++; //公共路径长度+1
times++;
break;
}
else if (b[x] == a[y]) {
pathnum++; //公共路径长度+1
break;
}
else continue;
}
}
return la + lb - 2 * pathnum + 1;
}
int returnRoot(int ID, int pathNum)
{
if (ID == 0) //回到根节点
{
qq[i].pathNum = pathNum; //记录到根之间的距离
return pathNum;
}
else
{
qq[i].path[top] = node[ID].parentID;//记录返回根之间需要经过的节点ID
top++;
returnRoot(node[ID].parentID, pathNum + 1);
}
}
void CreateTreeNode(FILE* fp)
{
while (n--)
{
fscanf(fp, "%d %d %d %d", &ID, &type, &parentID, &portNumber); //录入数据
if (parentID == -1) //录入根节点信息
{
node[0].ID = node[0].type = 0;
node[0].parentID = node[0].portNumber = -1;
}
else //录入一般节点信息
{
node[ID].ID = ID;
node[ID].type = type;
node[ID].parentID = parentID;
node[ID].portNumber = portNumber;
node[parentID].child[portNumber] = &node[ID];//树形数组相连,巧妙模拟树
}
}
}
void SortTree(Treep root)
{
int j;
CreateQueue(root); //构造前序遍历的存储队列
for (j = 0; j <= 7; j++)
{
if (root->child[j] != NULL)
{
SortTree(root->child[j]);//进行递归
}
}
return;
}
void CreateQueue(Treep root) //构造队列录入信息
{
q[head].ID = root->ID;
q[head].type = root->type;
q[head].portNumber = root->portNumber;
q[head].parentID = root->parentID;
q[head].when = head;//记录前序遍历的时间
head++;
}
int cmp(const void* p1, const void* p2)
{
struct queue* a = (struct queue*)p1;
struct queue* b = (struct queue*)p2;
if (a->pathNum != b->pathNum) return a->pathNum - b->pathNum; //先比两节点的距离
else return a->when - b->when; //再比前序遍历的时间
}
本题较为困难,与2024年春BUAA数据结构期末编程题第三题难度相当。考场上能做出的基本少之又少。
补充样例:
样例输入:
38 37
in.txt中的信息如下:
0 0 -1 -1
1 0 0 0
2 0 1 2
3 1 1 5
4 0 0 1
5 1 4 0
6 2 2 2
7 0 4 2
8 0 0 4
9 0 2 0
10 0 9 0
11 2 10 3
12 0 9 2
13 0 7 0
14 0 13 0
15 2 7 3
16 0 8 1
17 0 16 0
18 1 17 5
19 1 9 5
20 0 12 1
21 1 14 1
22 1 14 2
23 1 13 2
24 1 12 5
25 0 20 1
26 1 20 2
27 0 14 7
28 0 16 1
29 1 4 3
30 0 16 7
31 0 28 0
32 2 31 0
33 1 30 2
34 1 31 2
35 0 31 5
36 1 35 3
37 1 8 7
样例输出:
6 8 0 1 2
下面看一些作业题:
应用7-树叶节点遍历(树-基本题)
【问题描述】
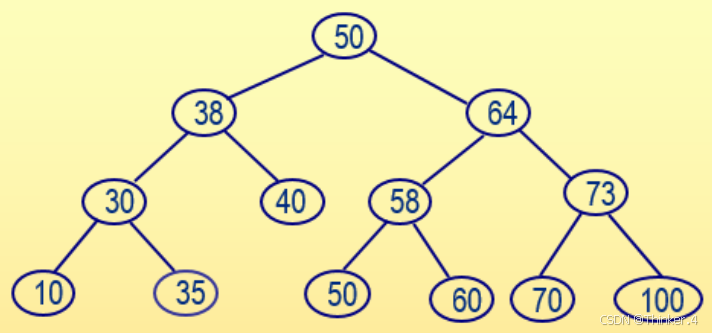
从标准输入中输入一组整数,在输入过程中按照左子结点值小于根结点值、右子结点值大于等于根结点值的方式构造一棵二叉查找树,然后从左至右输出所有树中叶结点的值及高度(根结点的高度为1)。例如,若按照以下顺序输入一组整数:50、38、30、64、58、40、10、73、70、50、60、100、35,则生成下面的二叉查找树:
从左到右的叶子结点包括:10、35、40、50、60、70、100,叶结点40的高度为3,其它叶结点的高度都为4。
【输入形式】
先从标准输入读取整数的个数,然后从下一行开始输入各个整数,整数之间以一个空格分隔。
【输出形式】
按照从左到右的顺序分行输出叶结点的值及高度,值和高度之间以一个空格分隔。
【样例输入】
13
50 38 30 64 58 40 10 73 70 50 60 100 35
【样例输出】
10 4
35 4
40 3
50 4
60 4
70 4
100 4
【样例说明】
按照从左到右的顺序输出叶结点(即没有子树的结点)的值和高度,每行输出一个。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
typedef struct _node {
int num;
struct _node* left, * right;
int depth;
}Node;
void insert(Node** t, int num, int depth);
void inOrderTraverse(Node* t);
int main()
{
int cnt;
int i;
int num;
Node* t = NULL;
scanf("%d", &cnt);
for (i = 0; i < cnt; i++) {
scanf("%d", &num);
insert(&t, num, 1);
}
inOrderTraverse(t);
return 0;
}
void insert(Node** t, int num, int depth) {
if (*t == NULL) {
*t = (Node*)malloc(sizeof(Node));
(*t)->num = num;
(*t)->left = NULL;
(*t)->right = NULL;
(*t)->depth = depth;
}
else if (num < (*t)->num) {
insert(&(*t)->left, num, depth + 1);
}
else {
insert(&(*t)->right, num, depth + 1);
}
}
void inOrderTraverse(Node* t) {
if (t != NULL) {
inOrderTraverse(t->left);
if (t->left == NULL && t->right == NULL) {
printf("%d %d\n", t->num, t->depth);
}
inOrderTraverse(t->right);
}
}
应用8-计算器(表达式计算-表达式树实现)
【问题描述】
从标准输入中读入一个整数算术运算表达式,如24 / ( 1 + 2 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 )= ,计算表达式结果,并输出。
要求:
1、表达式运算符只有+、-、*、/,表达式末尾的=字符表示表达式输入结束,表达式中可能会出现空格;
2、表达式中会出现圆括号,括号可能嵌套,不会出现错误的表达式;
3、出现除号/时,以整数相除进行运算,结果仍为整数,例如:5/3结果应为1。
4、要求采用表达式树来实现表达式计算。
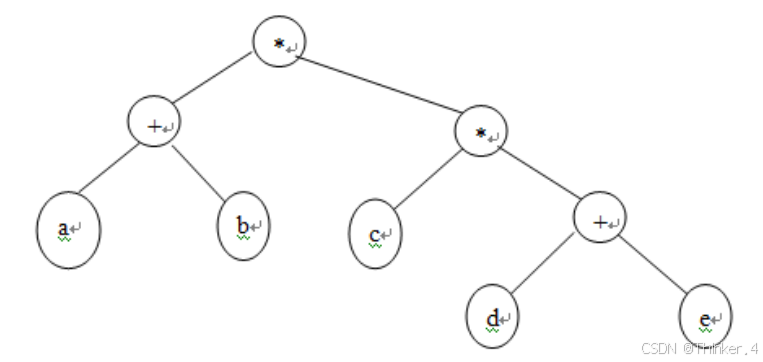
表达式树(expression tree):
我们已经知道了在计算机中用后缀表达式和栈来计算中缀表达式的值。在计算机中还有一种方式是利用表达式树来计算表达式的值。表达式树是这样一种树,其根节点为操作符,非根节点为操作数,对其进行后序遍历将计算表达式的值。由后缀表达式生成表达式树的方法如下:
l 读入一个符号:
l 如果是操作数,则建立一个单节点树并将指向他的指针推入栈中;
l 如果是运算符,就从栈中弹出指向两棵树T1和T2的指针(T1先弹出)并形成一棵新树,树根为该运算符,它的左、右子树分别指向T2和T1,然后将新树的指针压入栈中。
例如输入的后缀表达为:
ab+cde+**
则生成的表达式树为:
【输入形式】
从键盘输入一个以=结尾的整数算术运算表达式。操作符和操作数之间可以有空格分隔。
【输出形式】
首先在屏幕上输出表达式树根、左子节点及右子节点上的运算符或操作数,中间由一个空格分隔,最后有一个回车(如果无某节点,则该项不输出)。然后输出表达式计算结果。
【样例输入】
24 / ( 1 + 2 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 ) =
【样例输出】
* / /
18
【样例说明】
按照运算符及括号优先级依次计算表达式的值。在生成的表达树中,*是根节点的运算符,/ 是根节点的左子节点上运算符,/是根节点的右子节点上运算符,按题目要求要输出。
【评分标准】
通过所有测试点得满分。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
typedef struct _sign {
char sign;
int prior;
}Sign;
typedef struct _postNode {
Sign sign;
struct _postNode* next;
}postNode;
typedef struct _treenode {
char sign;
struct _treenode* left, * right;
}TreeNode;
void OrderStackPush(postNode** top, Sign sign);
char OrderStackPop(postNode** top);
int Cal(int num1, int num2, char sign);
int main()
{
char exp[100] = { 0 };
int i, j;
int digit;
int num1, num2, num;
char temp;
Sign sign;
postNode* postTop = NULL;
int calculate[100] = { 0 };
int calTop = -1;
TreeNode tree[100] = { 0 };
int treeTop = -1;
TreeNode* tempTree = NULL;
TreeNode* tree1, * tree2, * newTree;
tree1 = tree2 = newTree = NULL;
fgets(exp, 100, stdin);
for (i = 0; i < strlen(exp); i++) {
tempTree = (TreeNode*)malloc(sizeof(TreeNode));
tree1 = (TreeNode*)malloc(sizeof(TreeNode));
tree2 = (TreeNode*)malloc(sizeof(TreeNode));
//处理数字
digit = 0;
if (isdigit(exp[i])) {
while (isdigit(exp[i])) {
digit = digit * 10 + exp[i] - '0';
i++;
}
//printf("%d", digit);
//入数字栈
calculate[++calTop] = digit;
//入树栈
tempTree->sign = digit + '0';
tempTree->left = tempTree->right = NULL;
tree[++treeTop] = *tempTree;
}
//如果是“=”,读取结束
if (exp[i] == '=') {
break;
}
//以防万一,处理空格
if (exp[i] == ' ') {
continue;
}
//构造四则运算的优先级结构
switch (exp[i]) {
case'+':sign.sign = '+';
sign.prior = 1;
break;
case'-':sign.sign = '-';
sign.prior = 1;
break;
case'*':sign.sign = '*';
sign.prior = 2;
break;
case'/':sign.sign = '/';
sign.prior = 2;
break;
}
//如果是左括号,直接压栈
if (exp[i] == '(') {
sign.sign = '(';
sign.prior = 0;
OrderStackPush(&postTop, sign);
continue;
}
//如果是右括号,依次出栈到左括号
if (exp[i] == ')') {
while (postTop->sign.sign != '(') {
temp = OrderStackPop(&postTop);
//printf("%c", temp);
num1 = calculate[calTop--];
num2 = calculate[calTop--];
num = Cal(num1, num2, temp);
calculate[++calTop] = num;
//树操作
*tree1 = tree[treeTop--];
*tree2 = tree[treeTop--];
newTree = (TreeNode*)malloc(sizeof(TreeNode));
newTree->sign = temp;
newTree->left = tree2;
newTree->right = tree1;
tree[++treeTop] = *newTree;
}
temp = OrderStackPop(&postTop);
continue;
}
//如果是四则运算,比较优先级,如果优先级高于栈顶元素,
//直接压栈,否则依次出栈,直到遇到比自己优先级低的,压栈
while (postTop!=NULL && postTop->sign.prior >= sign.prior) {
temp = OrderStackPop(&postTop);
//printf("%c", temp);
num1 = calculate[calTop--];
num2 = calculate[calTop--];
num = Cal(num1, num2, temp);
calculate[++calTop] = num;
//树操作
*tree1 = tree[treeTop--];
*tree2 = tree[treeTop--];
newTree = (TreeNode*)malloc(sizeof(TreeNode));
newTree->sign = temp;
newTree->left = tree2;
newTree->right = tree1;
tree[++treeTop] = *newTree;
}
OrderStackPush(&postTop, sign);
}
//依次出栈
while (postTop != NULL) {
temp = OrderStackPop(&postTop);
//printf("%c", temp);
num1 = calculate[calTop--];
num2 = calculate[calTop--];
num = Cal(num1, num2, temp);
calculate[++calTop] = num;
//树操作
*tree1 = tree[treeTop--];
*tree2 = tree[treeTop--];
newTree = (TreeNode*)malloc(sizeof(TreeNode));
newTree->sign = temp;
newTree->left = tree2;
newTree->right = tree1;
tree[++treeTop] = *newTree;
}
printf("%c %c %c\n", tree[0].sign, tree[0].left->sign, tree[0].right->sign);
printf("%d", calculate[0]);
return 0;
}
void OrderStackPush(postNode** top, Sign sign) {
postNode* p = (postNode*)malloc(sizeof(postNode));
p->sign = sign;
p->next = *top;
*top = p;
}
char OrderStackPop(postNode** top) {
char temp = (*top)->sign.sign;
postNode* p = *top;
*top = (*top)->next;
free(p);
return temp;
}
int Cal(int num1, int num2, char sign) {
int num;
switch (sign) {
case'+':num = num2 + num1; break;
case'-':num = num2 - num1; break;
case'*':num = num2 * num1; break;
case'/':num = num2 / num1; break;
}
return num;
}
应用9-词频统计(树实现)
【问题描述】
编写程序统计一个英文文本文件中每个单词的出现次数(词频统计),并将统计结果按单词字典序输出到屏幕上。
要求:程序应用二叉排序树(BST)来存储和统计读入的单词。
注:在此单词为仅由字母组成的字符序列。包含大写字母的单词应将大写字母转换为小写字母后统计。在生成二叉排序树不做平衡处理。
【输入形式】
打开当前目录下文件article.txt,从中读取英文单词进行词频统计。
【输出形式】
程序应首先输出二叉排序树中根节点、根节点的右节点及根节点的右节点的右节点上的单词(即root、root->right、root->right->right节点上的单词),单词中间有一个空格分隔,最后一个单词后没有空格,直接为回车(若单词个数不足三个,则按实际数目输出)。
程序将单词统计结果按单词字典序输出到屏幕上,每行输出一个单词及其出现次数,单词和其出现次数间由一个空格分隔,出现次数后无空格,直接为回车。
【样例输入】
当前目录下文件article.txt内容如下:
“Do not take to heart every thing you hear.”
“Do not spend all that you have.”
“Do not sleep as long as you want;”
【样例输出】
do not take
all 1
as 2
do 3
every 1
have 1
hear 1
heart 1
long 1
not 3
sleep 1
spend 1
take 1
that 1
thing 1
to 1
want 1
you 3
【样例说明】
程序首先在屏幕上输出程序中二叉排序树上根节点、根节点的右子节点及根节点的右子节点的右子节点上的单词,分别为do not take,然后按单词字典序依次输出单词及其出现次数。
【评分标准】
通过全部测试点得满分
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <ctype.h>
#include <stdlib.h>
typedef struct _tnode {
char word[20];
int cnt;
struct _tnode* left, * right;
}tNode;
void insert(tNode** t, char word[]);
void inorderTraverseBST(tNode* t);
int main()
{
FILE* fp = fopen("article.txt", "r");
char sentence[1024] = { 0 }; //每次读入一行
char word[20] = { 0 };
int i, j;
tNode* root = NULL;
//readin
while (fgets(sentence, 1024, fp) != NULL) {
for (i = 0; i < strlen(sentence); i++) {
if (isalpha(sentence[i])) {
j = 0;
while (isalpha(sentence[i])) {
word[j++] = tolower(sentence[i++]);
}
//插入树中
insert(&root, word);
//清空word
for (j = 0; j < 20; j++) {
word[j] = '\0';
}
}
}
//清空sentence
for (i = 0; i < 1024; i++) {
sentence[i] = '\0';
}
}
if (root != NULL) {
printf("%s ", root->word);
}
if (root->right != NULL) {
printf("%s ", root->right->word);
}
if (root->right->right != NULL) {
printf("%s ", root->right->right->word);
}
printf("\n");
inorderTraverseBST(root);
fclose(fp);
return 0;
}
void insert(tNode** t, char word[]) {
if (*t == NULL) {
*t = (tNode*)malloc(sizeof(tNode));
strcpy((*t)->word, word);
(*t)->cnt = 1;
(*t)->left = (*t)->right = NULL;
}
else {
if (strcmp((*t)->word, word) > 0) {
insert(&((*t)->left), word);
}
else if (strcmp((*t)->word, word) < 0) {
insert(&((*t)->right), word);
}
else {
(*t)->cnt++;
}
}
}
void inorderTraverseBST(tNode* t) {
if (t != NULL) {
inorderTraverseBST(t->left);
printf("%s %d\n", t->word, t->cnt);
inorderTraverseBST(t->right);
}
}
以上就是全部内容。树是难点也是BUAA数据结构期末必考的难题,请大家一定认真掌握。