前置：

看到这的你估计已经熟练了一维前缀和，那么我们向二维空间扩展一下

a[x][y]表示当前(x,y)的值

pre[x][y]表示(x,y)左上部分的前缀和

要求计算(x1,y1)到(x2,y2)这一部分的前缀和

公式：

pre[x2, y2] - pre[x1 - 1, y2] - pre[x2, y1 - 1] + pre[x1 - 1, y1 - 1]

模板：

不墨迹先上模板再证明

const int M = 1005;
int n,m,q;
ll a[M][M],pre[M][M];
void init(int n,int m){
    for(int x=1;x<=n;x++)
        for(int y=1;y<=m;y++){
            cin>>a[x][y];
            pre[x][y]=a[x][y]+pre[x-1][y]+pre[x][y-1]-pre[x-1][y-1];
        }
}
ll query(int Lx,int Rx,int Ly,int Ry){  
    return pre[Ly][Ry]-pre[Lx-1][Ry]-pre[Ly][Rx-1]+pre[Lx-1][Rx-1];
} 
void solve(){
    cin>>n>>m>>q;
    init(n,m);
    while(q--){
        int Lx,Rx,Ly,Ry;
        cin>>Lx>>Rx>>Ly>>Ry;
        cout<<query(Lx,Rx,Ly,Ry)<<"\n";
    }
}

图文讲解（证明）：

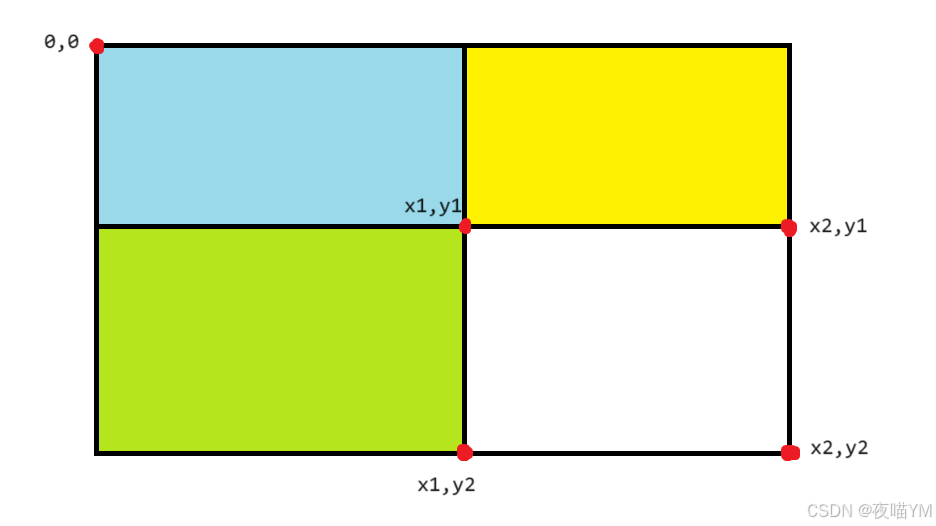
（众所周知黄+绿=蓝）

pre[x2][y2]=蓝+黄+绿+白

pre[x1-1][y2]=绿+蓝

pre[x2][y1-1]=黄+蓝

pre[x1-1,y1-1]=蓝

res=pre[x2,y2] - pre[x1-1,y2] - pre[x2,y1-1] + pre[x1-1, y1-1]

     =(蓝+黄+绿+白)-(绿+蓝)-(黄+蓝)+(蓝)

     =白

我们要的是白色部分的结果，显而易见证明了公式