数学建模--智能算法之模拟退火算法

初始化：选择一个初始解，并设置初始温度T和冷却率α。
迭代过程：
在当前温度T下，随机生成一个新的解x'。
计算目标函数值ΔE = f(x') - f(x)，其中f(x)为目标函数。
如果ΔE < 0，则接受新解x'；否则以概率exp(-ΔE/(kT))接受新解x'，其中k为玻尔兹曼常数。
降温过程：根据冷却率α降低温度T，即T = αT。
终止条件：当温度T降至某个阈值时停止迭代。

应用场景

模拟退火算法适用于解决复杂的组合优化问题，如旅行商问题（TSP）、装箱问题、图着色问题等。它能够有效跳出局部最优解，寻找全局最优解。

实现方法

在实际应用中，模拟退火算法可以通过编程实现。常用的编程语言包括Python和Matlab。

代码示例：

MATLAB：

function [bestX, bestY] = simulatedAnnealing(f, x0, T0, alpha)
% 初始化参数
x = x0;
y = f(x);
bestX = x;
bestY = y;
T = T0;

while T > 1e-6
% 随机扰动当前解
xNew = perturb(x);
yNew = f(xNew);
        
% 判断是否接受新解
if yNew < y || rand() < exp(-(yNew - y)/T)
x = xNew;
y = yNew;
end
        
% 更新最佳解
if yNew < bestY
bestY = yNew;
bestX = xNew;
end
        
% 降温
T = T * alpha;
end
end

function y = f(x)
% 目标函数定义
y = -sum(x.^2);
end

function xNew = perturb(x)
% 扰动操作
xNew = x + randn(size(x));
end

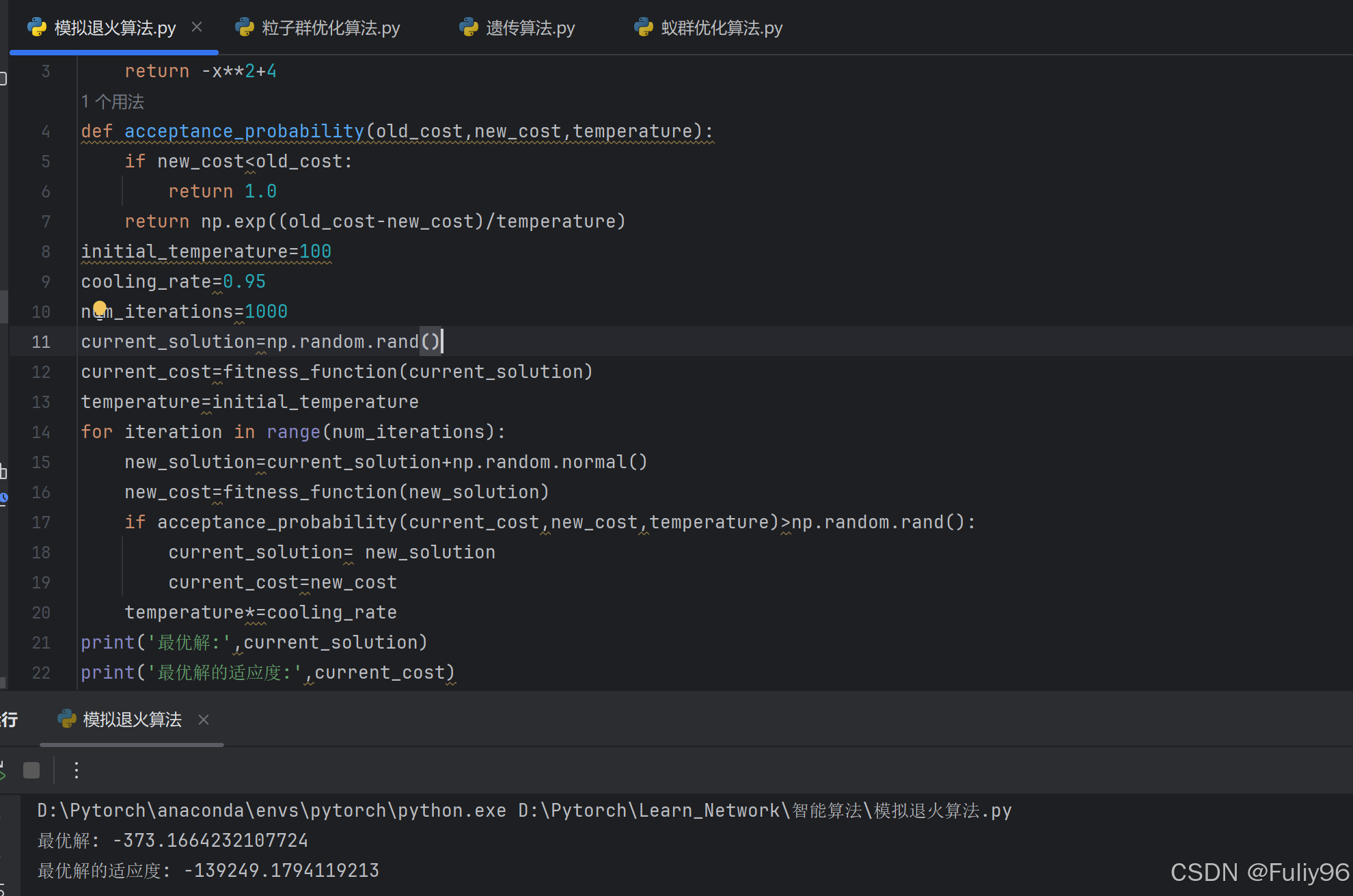
Python：

import numpy as np

def fitness_function(x):
    return -x**2 + 4

def acceptance_probability(old_cost, new_cost, temperature):
    if new_cost < old_cost:
        return 1.0
    return np.exp((old_cost - new_cost) / temperature)

# 初始化参数
initial_temperature = 100
cooling_rate = 0.95
num_iterations = 1000

# 初始化解
current_solution = np.random.rand()
current_cost = fitness_function(current_solution)

# 模拟退火主循环
temperature = initial_temperature
for iteration in range(num_iterations):
    new_solution = current_solution + np.random.normal()
    new_cost = fitness_function(new_solution)
    
    if acceptance_probability(current_cost, new_cost, temperature) > np.random.rand():
        current_solution = new_solution
        current_cost = new_cost
    
    temperature *= cooling_rate

# 结果
print("最优解:", current_solution)
print("最优适应度:", current_cost)

总结

模拟退火算法通过模拟物理退火过程中的温度逐步下降，结合概率接受机制，能够在解空间中随机搜索并逐步逼近全局最优解。其简单易行且适用范围广，是解决复杂优化问题的有效工具。

模拟退火算法在数学建模中的具体应用案例有哪些？

        模拟退火算法在数学建模中的具体应用案例主要集中在优化问题的求解上，特别是在那些需要找到全局最优解的问题中表现尤为突出。以下是几个具体的案例：

        在数学建模比赛中，利用模拟退火算法解决寝室分配问题是一个典型的例子。该问题涉及到如何将学生分配到不同的寝室以达到最优配置，例如最小化学生之间的距离差异、最大化空间利用率等。

        模拟退火算法常用于解决各种组合优化问题，如旅行商问题（TSP）、车辆路径问题（VRP）等。这些问题通常具有庞大的搜索空间和复杂的约束条件，通过模拟退火算法可以在较短时间内找到近似最优解。

        在工程设计领域，模拟退火算法被广泛应用于结构优化、机械设计等领域。例如，在桥梁设计中，通过模拟退火算法可以优化梁的截面形状和材料分布，从而提高结构的稳定性和经济性。

        在图像处理和计算机视觉中，模拟退火算法也被用于图像分割、特征提取等问题。通过模拟退火算法，可以有效地从大量可能的解决方案中找到最佳的图像分割方案或特征点。

        这些案例展示了模拟退火算法在数学建模中的广泛应用，其核心优势在于能够处理高维度、非线性、多峰值的复杂优化问题，并且能够在有限的时间内找到近似最优解。

如何选择模拟退火算法的参数（如初始温度、冷却率等）以优化求解过程？

        选择模拟退火算法的参数（如初始温度、冷却率等）以优化求解过程，需要综合考虑多个因素，并根据具体问题进行调整。以下是详细的建议：

        初始温度是影响全局搜索能力的重要参数。较高的初始温度可以增加接受劣解的概率，从而允许算法进行更广泛的全局搜索，但同时也会导致计算时间的增加。常见的初始温度设置为1000或5000。一般情况下，初始温度越高，能够接受更多的劣解，但搜索速度会变慢。

        终止温度通常设置为一个较小的值，例如1e-8，表示当温度降至该值时停止迭代。这个参数决定了算法何时结束，过高的终止温度可能导致算法未能充分探索解空间，而过低的终止温度则可能使算法陷入局部最优解。

        降温速率控制了温度在每次迭代中的衰减速度。合适的降温速率可以平衡全局搜索和局部搜索的能力。常用的降温方式包括指数降温、线性降温和对数降温等。艾印双等人提出的自适应降温方式可以根据不同参数的变化范围和收敛速度来决定每次迭代的退火温度。

        步长控制了在每个温度下进行多少次迭代。较大的步长可以加快收敛速度，但可能会错过一些好的解；较小的步长则可以提高精度，但会增加计算量。

其他参数：

在实际应用中，可以通过交叉对比的方法来优化参数设置。例如，在处理TSP问题时，可以使用不同的初始温度、降温速率和步长进行多次实验，比较其性能差异，从而找到最优的参数组合。

状态空间和目标函数：明确问题的状态空间和目标函数是基础，这将直接影响算法的有效性和准确性。
候选生成器过程：选择合适的候选生成器过程可以提高算法的效率和效果。
接受概率函数：设计合理的接受概率函数可以确保算法在不同温度下的行为符合预期。

总之，模拟退火算法的参数设置没有固定的规律，需要根据具体问题的特点和实验结果不断调整和优化。

模拟退火算法与其他优化算法（如遗传算法、粒子群优化等）相比，有哪些优势和劣势？

模拟退火算法（SA）与其他优化算法（如遗传算法、粒子群优化等）相比，具有以下优势和劣势：

优势：

全局搜索能力：模拟退火算法通过引入随机性和温度控制机制，能够在搜索过程中以一定的概率接受劣解，从而避免陷入局部最优解，增加了全局搜索的能力。
鲁棒性强：由于其计算过程简单且通用，模拟退火算法在处理复杂的非线性优化问题时表现出较强的鲁棒性。（鲁棒性指的是算法对数据中的噪声、异常值和扰动的抵抗能力）
适用于大规模问题：模拟退火算法可以处理大量的变量和约束条件，适用于大规模问题的求解。
并行处理能力：该算法适用于并行处理，能够提高计算效率。

劣势：

收敛速度慢：模拟退火算法需要较长的执行时间，尤其是在退火计划较长的情况下，可能需要很长时间才能收敛到最优解。
参数敏感：算法性能与初始值有关，对参数设置较为敏感，需要仔细调整以获得较好的结果。
可能不如其他算法有效：对于某些复杂的问题，模拟退火算法的效果可能不如其他优化算法，如遗传算法或粒子群优化算法。

总结来说，模拟退火算法在全局搜索能力和鲁棒性方面具有显著优势，但其收敛速度慢和参数敏感性是其主要劣势。

在实际工程问题中，模拟退火算法的实施步骤和技巧有哪些？

在实际工程问题中，模拟退火算法的实施步骤和技巧如下：

实施步骤

初始化：
- 生成初始解 x(0)x(0)，并为每个参数分配随机值（在约束范围内）。
- 设置初始温度 T(0)T(0)，通常建议值为较大值如1000，以确保能够充分“熔化”初始参数估计值。
循环过程：
- 在每次迭代中，通过扰动函数生成候选解 p′p′，并计算其对应的残差误差或能量变化量 ΔEΔE。
- 判断是否接受新解：如果 ΔE≤0ΔE≤0，则直接接受新解；否则，根据Metropolis准则，即概率 exp⁡(−ΔE/T)exp(−ΔE/T) 接受新解。
- 更新温度 TT，通常采用指数冷却策略，即 Tnew=αToldTnew=αTold，其中 α<1α<1。
终止条件：

循环直到温度低于某个阈值 TminTmin，例如 Tmin=10−5Tmin=10−5。

技巧

火焰温度降低策略：
- 使用指数冷却策略，即 Tnew=αToldTnew=αTold，其中 α<1α<1。
- 可以使用线性冷却策略，即 Tnew=Told−βTnew=Told−β，其中 β>0β>0。
接受准则的选择：
- Metropolis准则：粒子在温度 TT 时趋于平衡的概率为 exp⁡(−ΔE/T)exp(−ΔE/T)。
- 硬性约束条件的处理方法：在每次迭代中检查是否满足所有硬性约束条件，若不满足则拒绝该解。
卡时技巧：

模拟退火算法需要多次运行才能找到最优解。为了节省时间，可以使用 (clock())(clock()) 函数来判断剩余时间，并适时停止算法。
参数调节技巧：
- 调整初始温度和冷却速率，以找到最佳的退火路径，从而提高算法效率。
- 对于不同的优化问题，选择合适的参数范围和初始值，以确保算法的有效性。

模拟退火算法在解决特定类型问题时的局限性是什么？

模拟退火算法（Simulated Annealing, SA）是一种基于统计物理学固体退火原理的全局搜索优化算法，尽管其具有一定的通用性和灵活性，但在解决特定类型问题时仍存在一些局限性。以下是模拟退火算法在实际应用中的一些主要局限性：

收敛速度慢：模拟退火算法需要较长的时间才能收敛到最优解，这使得它在处理大规模或复杂问题时效率较低。此外，当采样数很大时，算法的收敛效率更低，运算时间长，进一步限制了其实际应用。

参数调整困难：模拟退火算法的性能高度依赖于初始温度、冷却率和停止条件等参数的选择。这些参数的调整较为困难，通常需要多次实验和分析才能确定最优参数。不同问题可能需要不同的初始解和参数设置，增加了算法使用的复杂度。

全局最优解的不确定性：虽然理论上模拟退火算法能够以概率1收敛于评价函数的最优值，但实际应用中由于初始状态和参数选择的影响，可能会陷入局部最优解而不是全局最优解。这种对初始状态敏感的特点使得算法在某些情况下难以找到真正的全局最优解。

计算资源需求高：模拟退火算法在进行大规模优化问题求解时，需要大量的计算资源，特别是在处理组合优化问题时，其计算效率低下的缺点更加明显。这也限制了其在需要快速结果的应用场景中的使用。

适用范围有限：虽然模拟退火算法适用于难以求导和导数不存在的优化问题，但在面对更复杂、极值点更多的函数时，其效果可能不如其他优化方法理想。例如，在恢复种植解方面，模拟退火法被玻璃态所吸引，而玻璃态并不影响置信度，因此在某些特定领域表现次优。