线性回归模型
这个可能是当今世界上使用最广泛的学习算法
x x x—> f f f—> y ^ \hat{y} y^
这里的 f f f 我们称之为模型
那么,我们该如何求出这个 f f f 呢?
让我们从线性函数开始
假设这个模型为 f ( x ) = w x + b f(x)=w x+b f(x)=wx+b
w 、 b w、b w、b被称为模型的参数,在机器学习中,模型的参数是你可以在训练期间调整以改进模型的变量,也叫系数或者权重
成本函数
在机器学习中,不同的人会针对不同的应用程序使用不同的成本函数,但是平方误差成本函数是迄今为止线性回归最常用的函数
J ( w , b ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2 J(w,b)=\frac{1}{2m}\sum_{i=1}^{m} (\hat{y}^{(i)}-y^{(i)})^2 J(w,b)=2m1∑i=1m(y^(i)−y(i))2
这被称为平方误差成本函数(当然,除数中的2不写也依然成立)
这个函数也可以重写为这样
J ( w , b ) = 1 2 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) 2 J(w,b)=\frac{1}{2m}\sum_{i=1}^{m} (f(x^{(i)})-y^{(i)})^2 J(w,b)=2m1∑i=1m(f(x(i))−y(i))2
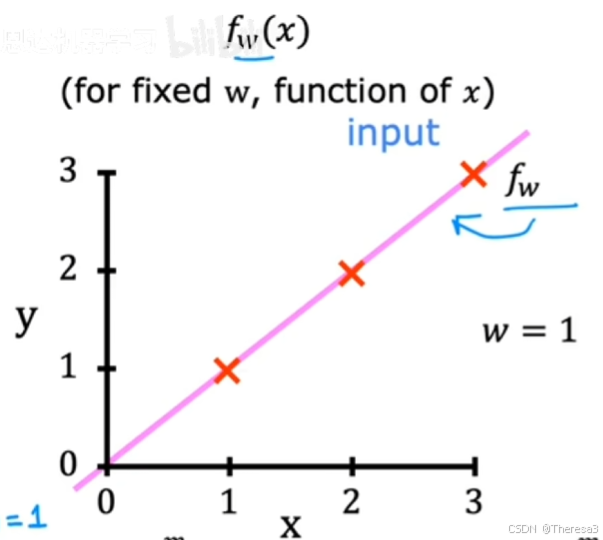
首先,让我们假设 b = 0 b=0 b=0,那么这个模型就简化为了一个正比例函数模型,成本函数就变成了关于 w w w的一元函数
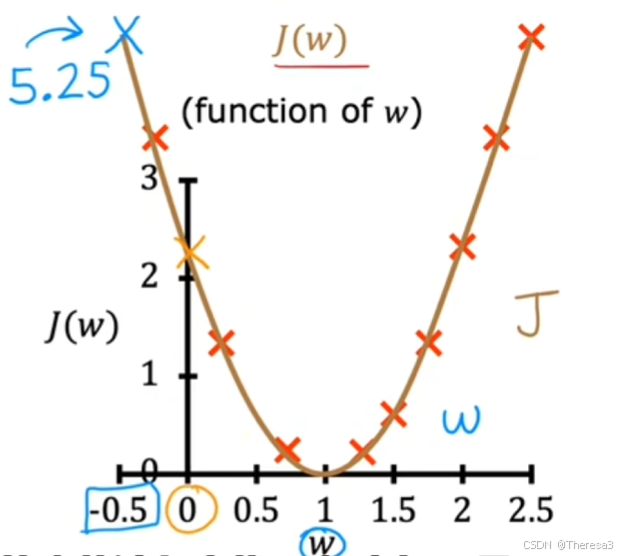
根据 w w w的不同取值,我们可以分别求出 J ( w ) J(w) J(w)的不同值,并画出其函数图像,如下图
那么,根据第二张图片,我们该选择 w w w的什么值,使其对图一的拟合效果更好呢?
当然是选择使 J ( w ) J(w) J(w)的值尽可能小的 w w w值,在这个例子中,也就是 w = 1 w=1 w=1
这就是线性回归中如何使用成本函数来找到 w w w取值的方法—>使成本函数 J ( w ) J(w) J(w)最小
好的,让我们回到原始模型,我们不将 b b b设置为0,这时候的 J ( w , b ) J(w,b) J(w,b)又是什么呢?
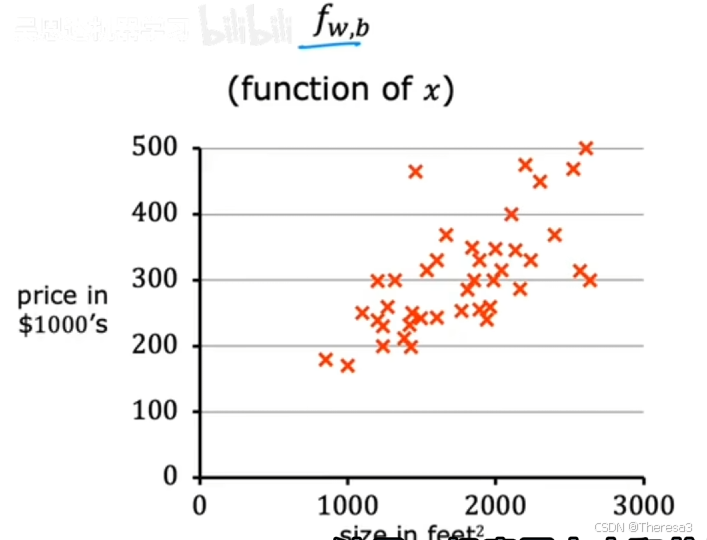
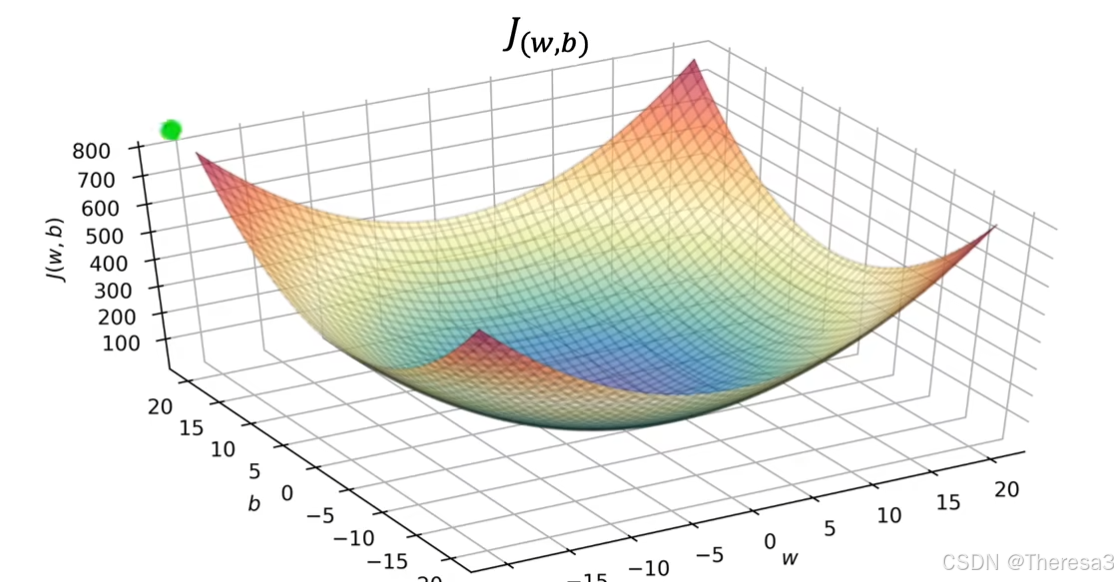
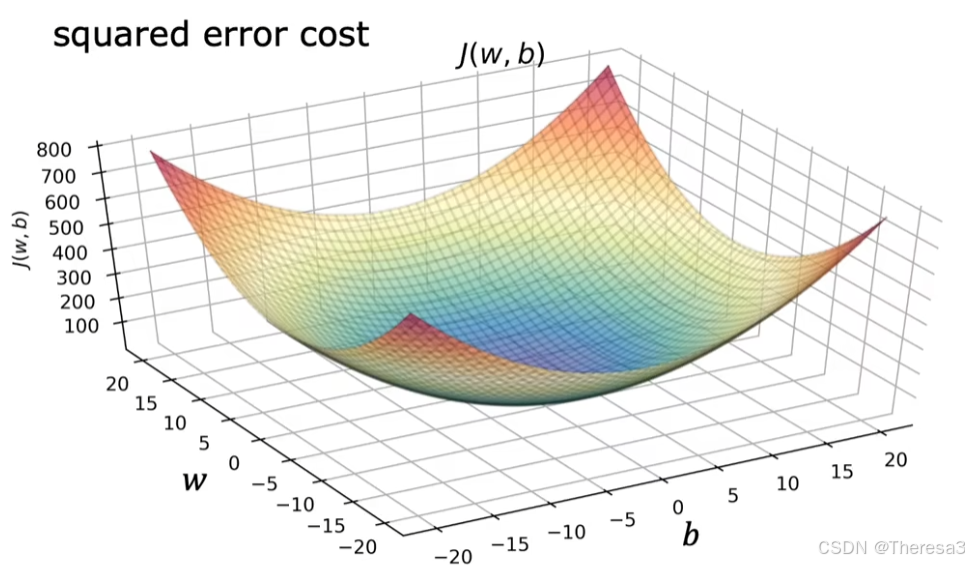
这是一组房屋大小和价格的训练集,和上面一样,我们根据 w 、 b w、b w、b的不同取值,可以作出成本函数 J ( w , b ) J(w,b) J(w,b)的函数图像,只是这个函数图像是一个三维图像(如图)
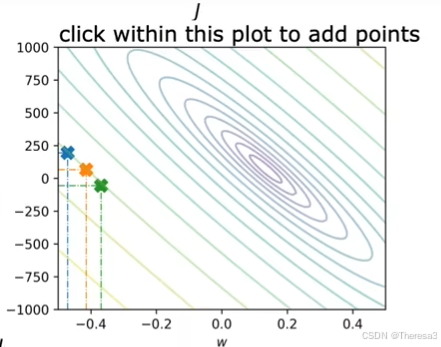
回忆一下初中地理学的等高线地形图吧,对于这个三维图像,我们仍然会用等高线图去进行表示(如图)
对于这个图来说,成本函数 J J J的最小值在这些同心椭圆的中心点处
接下来,我们就该思考了:有没有一种算法,可以通过代码来自动找到参数 w 、 b w、b w、b的值呢?
当然是有的,这种算法叫做梯度下降
梯度下降
毫无疑问,这个算法是机器学习中最重要的算法之一
梯度下降和梯度下降的变体不仅用于训练线性回归,还用于训练所有AI中一些最大和最复杂的模型
好了,我们先来回忆一下高等数学中的梯度的概念
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)
还记得梯度的计算方法吗?
g r a d f ( x , y ) = f x ( x , y ) i ⃗ + f y ( x , y ) j ⃗ grad f(x,y)=f_x(x,y)\vec i+f_y(x,y)\vec j gradf(x,y)=fx(x,y)i+fy(x,y)j
好了,我们现在开始研究梯度下降
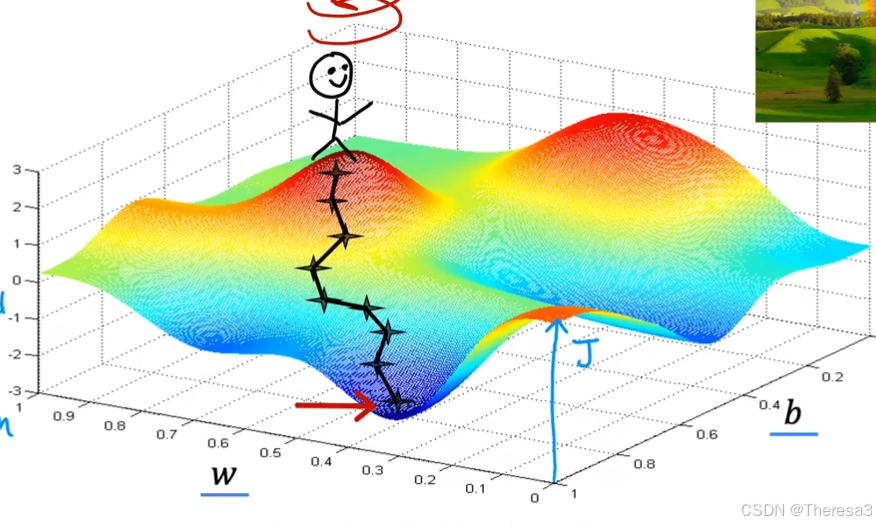
首先,我们通过为参数 w 、 b w、b w、b选择初始值来选择表面的起始点,然后我们沿着这个点的梯度方向迈出一步,不断循环这个步骤,直到我们处在这个山谷的最底部,那么,我们就得到了一个局部最小值(如图)
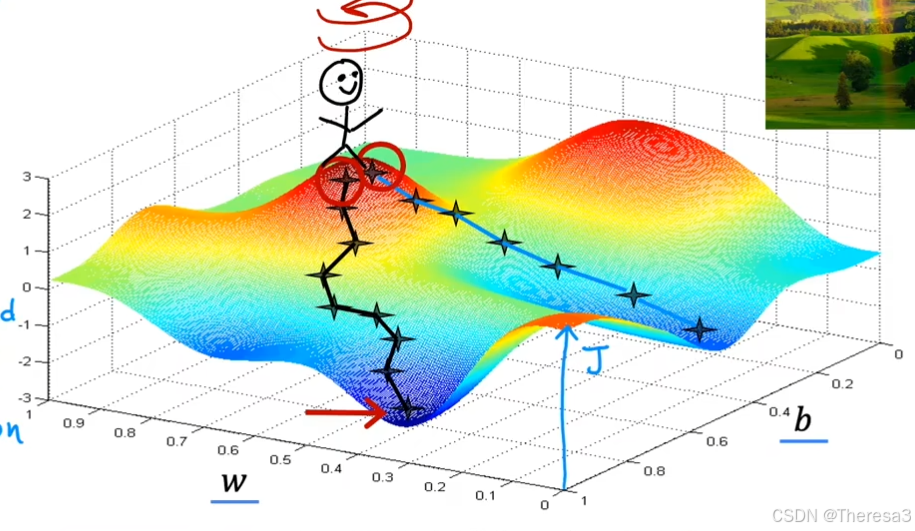
如果我们换一组 w 、 b w、b w、b的取值,重新尝试梯度下降呢?
或许我们会得到一个完全不一样的结果(如下图所示)
不过没有问题,我们得到的这两个甚至更多的值都被称为局部最小值
接下来,我们来讨论如何实现梯度下降算法
注意:在接下来的过程中 =被作为赋值运算符而不是等于号
梯度下降法则:
w = w − α ∂ ∂ w J ( w , b ) w=w-\alpha\frac{\partial}{\partial w}J(w,b) w=w−α∂w∂J(w,b)
b = b − α ∂ ∂ b J ( w , b ) b=b-\alpha\frac{\partial}{\partial b}J(w,b) b=b−α∂b∂J(w,b)
这里的 α \alpha α是学习率,学习率通常是0到1之间的一个正小数,它来控制这个算法下坡的步幅,这个数字越大,下坡的速度越快
如果学习率太小,梯度下降会起作用,但是速度会很慢
如果学习率太大,这个算法可能会过冲,并且可能永远不会达到最小值
另一种说法是,它可能无法收敛,甚至可能发散
我们将不断重复这两个更新步骤,直到算法收敛
- 正确的算法示例:
t e m p _ w = w − α ∂ ∂ w J ( w , b ) temp\_w=w-\alpha\frac{\partial}{\partial w}J(w,b) temp_w=w−α∂w∂J(w,b)
t e m p _ b = b − α ∂ ∂ b J ( w , b ) temp\_b=b-\alpha\frac{\partial}{\partial b}J(w,b) temp_b=b−α∂b∂J(w,b)
w = t e m p _ w w=temp\_w w=temp_w
b = t e m p _ b b=temp\_b b=temp_b
- 错误的算法示例:
t e m p _ w = w − α ∂ ∂ w J ( w , b ) temp\_w=w-\alpha\frac{\partial}{\partial w}J(w,b) temp_w=w−α∂w∂J(w,b)
w = t e m p _ w w=temp\_w w=temp_w
t e m p _ b = b − α ∂ ∂ b J ( w , b ) temp\_b=b-\alpha\frac{\partial}{\partial b}J(w,b) temp_b=b−α∂b∂J(w,b)
b = t e m p _ b b=temp\_b b=temp_b
注意:在每一步中, w 、 b w、b w、b必须同时更新,错误算法就是非同步更新,它先更新了 w w w,然后根据更新后的 w w w更新 b b b
用于线性回归的梯度下降
f ( x ) = w x + b f(x)=w x+b f(x)=wx+b
J ( w , b ) = 1 2 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) 2 J(w,b)=\frac{1}{2m}\sum_{i=1}^{m} (f(x^{(i)})-y^{(i)})^2 J(w,b)=2m1∑i=1m(f(x(i))−y(i))2
w = w − α ∂ ∂ w J ( w , b ) w=w-\alpha\frac{\partial}{\partial w}J(w,b) w=w−α∂w∂J(w,b)
b = b − α ∂ ∂ b J ( w , b ) b=b-\alpha\frac{\partial}{\partial b}J(w,b) b=b−α∂b∂J(w,b)
根据上面的这四个式子,我们可以推导出线性回归的梯度下降算法(推导过程就省略了,运用的微积分,希望你还记得它)
w = w − α 1 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) x ( i ) w=w-\alpha\frac{1}{m}\sum_{i=1}^{m} (f(x^{(i)})-y^{(i)})x^{(i)} w=w−αm1∑i=1m(f(x(i))−y(i))x(i)
b = b − α 1 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) b=b-\alpha\frac{1}{m}\sum_{i=1}^{m} (f(x^{(i)})-y^{(i)}) b=b−αm1∑i=1m(f(x(i))−y(i))
事实证明,当我们使用线/性回归的平方误差成本函数时,成本函数不会也永远不会出现多个局部最小值(如图)