接着上回的分享,继续分享一下图中比较重要的一类应用
那就是求最小生成树
最小生成树的定义
连通图中的每一棵生成树,都是原图的一个极大无环子图,即:从其中删去任何一条边,生成树
就不在连通;反之,在其中引入任何一条新边,都会形成一条回路。
若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三
条:
- 只能使用图中的边来构造最小生成树
- 只能使用恰好n-1条边来连接图中的n个顶点
- 选用的n-1条边不能构成回路
感性来说,最小生成树,就是所有边的权值和最小的生成树。
构造最小生成树主要有两种算法,分别是Kruskal算法和Prim算法
这两种算法都是基于贪心的策略,其中Kruskal算法偏向于全局贪心,而Prim算法则是偏向于局部贪心的算法。
但是,我们要知道的是,贪心算法往往是求得局部最优解,不一定是全局最优解,所以,一个图的最小生成树不一定存在,也可能有多棵。
求最小生成树的前置要求
当我们求出来了一颗最小生成树,我们如何保存它,
我们总不能存在原来的图里面吧,所以,我们首先要在搞一个新图,当然,我们在上一篇博客中提到,后续图相关算法我们都采用邻接矩阵的结构,这也一样。
创建好新图后,需要对新图进行初始化,将新图的_vertexs顶点数组和_indexMap都进行初始化,邻接矩阵就不用初始化了,将这个邻接矩阵填充完毕就是我们的任务
Kruskal算法
Kruskal算法为什么是一个偏向于全局贪心的算法呢?
且听我慢慢分析
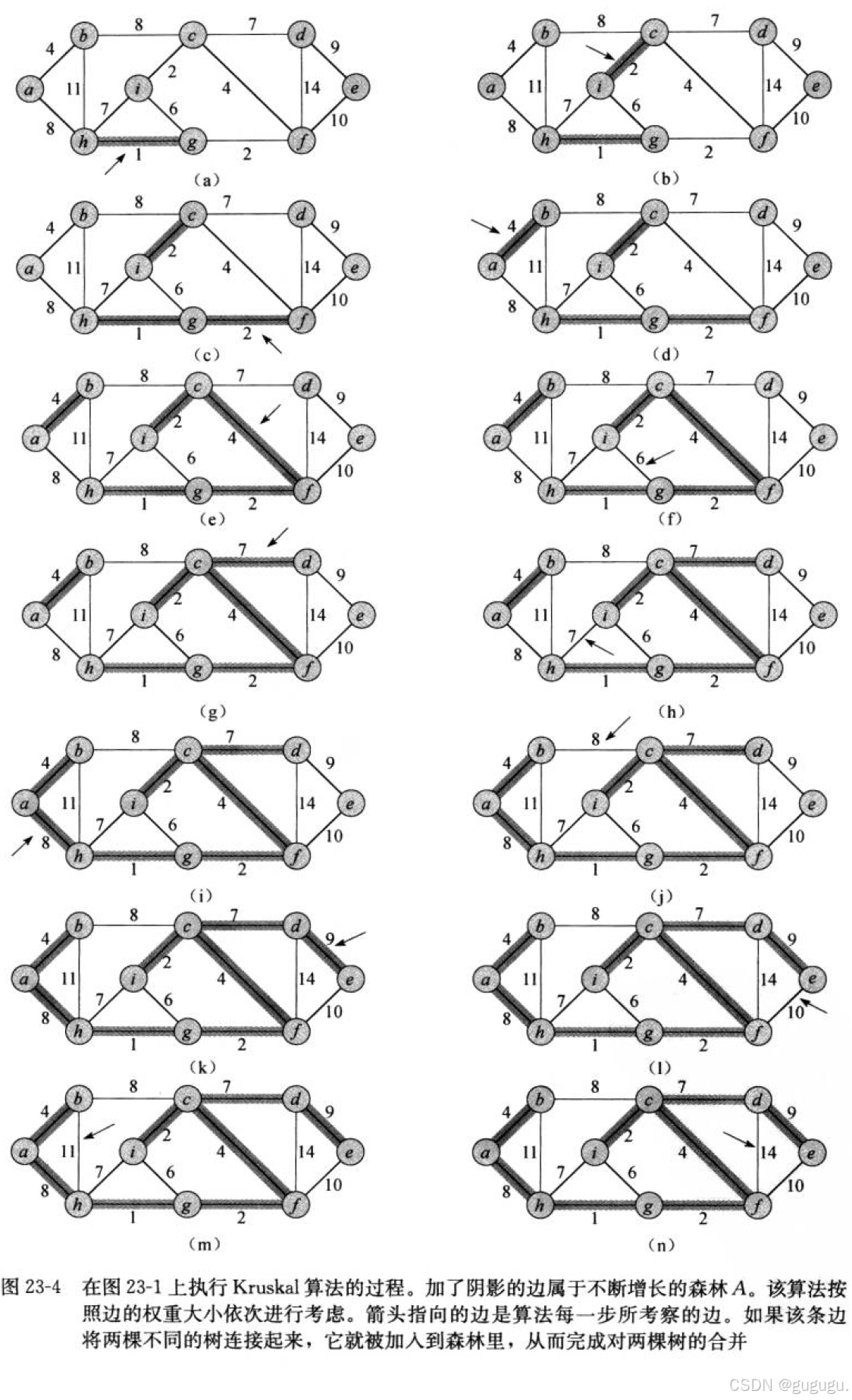
Kruskal算法,相当简单
就是每一次都去取最短的边
这样我们所构成的生成树的总权值就是最小的。
第一步
那么我们首先要对边进行排序,
这里我们直接用优先级队列priority_queue建小堆即可。
众所周知,在C++中priority_queue是默认建大堆的,所以,我们要去调整优先队列的参数
priority_queue的第一个参数是优先队列里面存的元素的类型,第二个参数是适配器类型,第三个参数是cmp比较仿函数
我们来一个一个参数的调整
首先,优先级队列里面存边,毫无疑问,那我们的邻接矩阵结构没有边这个类型啊,
显然,需要我们来自定义这个类型了。
template<class V,class W>
struct Edge//边的结构
{
int _srci;//起点的下标
int _dsti;//终点的下标
W _w;//权值
Edge(int srci, int dsti, W weight)
:_srci(srci)
, _dsti(dsti)
, _w(weight)
{}
};
所以第一个参数搞定了,Edge即可
第二个参数也顺带搞定,直接传vector<Edge>即可(这个其实就是一种适配器模式,不懂的可以去看看23种设计模式)
那么第三个参数,默认是less建大堆
所以,我们直接greater建小堆(当然,手写cmp仿函数也可)
注意细节,greater也是一个模版,在使用的时候也需要显示实例化,所以,第三个参数我们传的是greater<Edge>
通过优先级队列,我们建好了小堆,每次直接拿堆顶元素,取出最小的边
OK,我们第一步排序完成了。
第二步
接下来,我们想一想,生成树中是不是要求不能出现环啊,(生成树是一颗树)
那么如何避免成环呢?
Kruskal算法中使用的方法是利用数据结构并查集
传送门:数据结构:并查集
假设图中有n个顶点,n = _vertexs.size()
我们创建一个n个大小的并查集,
当两个顶点相连之后,就将他们在并查集中合并,
所以,想判断是否成环,只需要判断顶点是否在同一个集合,如果在同一个集合,就成环,那么这条边就不能参与构成最小生成树。
总结一下
Kruskal算法步骤其实就是
给新图初始化一下
首先创建一个优先队列,把所有的边全部入队列
接着创建并查集
接着就可以开始生成最小生成树了,
每次取优先队列顶的元素,丢进并查集,看看边的两个顶点是否在一个集合,
如果在一个集合,跳过这条边
如果不在这个集合,那就可以参与构成最小生成树,在新图的邻接矩阵中新加这条边
直到优先队列为空,结束算法
注意:我们在一开始就说过,最小生成树可能不存在,那么什么时候不存在呢?
我们设置两个变量,一个total(权值和),一个edgeSize(边的数量)
每次最小生成树创建新边的时候,更新这两个值
最后,如果edgeSize == n - 1说明,可以构成最小生成树,返回total
否则,返回W()默认值 ,(W是权值类型,W()是匿名对象的用法)
Kruskal算法代码
W Kruskal(Self& g)
{
g._vertexs = _vertexs;
g._indexMap = _indexMap;
g._weights.resize(_vertexs.size());
for (int i = 0; i < _vertexs.size(); ++i)
{
(g._weights[i]).resize(_vertexs.size(), MAX_W);
}
W total = 0;
int EdgeSize = 0;
priority_queue<Edge, vector<Edge>, greater<Edge>> pq;//建小堆
UFT::UnionFindSet uft(_vertexs.size());
for (int i = 0; i < _weights.size(); ++i)//把所有的边全部进入小堆
{
for (int j = 0; j < _weights[i].size(); ++j)
{
if (i < j && _weights[i][j] != MAX_W)
{
pq.push(Edge(i, j, _weights[i][j]));
}
}
}
while (!pq.empty())
{
Edge front = pq.top();
pq.pop();
bool ret = uft.IsSameSet(front._srci, front._dsti);
if (ret == false)
{
g.AddEdge(_vertexs[front._srci], _vertexs[front._dsti], front._w);
uft.Union(front._srci, front._dsti);//构造边之后,并查集也要合并集合
cout << _vertexs[front._srci] << "->" << _vertexs[front._dsti] << endl;
total += front._w;
EdgeSize++;
}
}
if (EdgeSize == _vertexs.size() - 1)
return total;
return W();
}
代码演示
测试代码
void TestGraphMinTree()
{
const char* str = "abcdefghi";
graph<char, int> g(str, strlen(str));
g.AddEdge('a', 'b', 4);
g.AddEdge('a', 'h', 8);
//g.AddEdge('a', 'h', 9);
g.AddEdge('b', 'c', 8);
g.AddEdge('b', 'h', 11);
g.AddEdge('c', 'i', 2);
g.AddEdge('c', 'f', 4);
g.AddEdge('c', 'd', 7);
g.AddEdge('d', 'f', 14);
g.AddEdge('d', 'e', 9);
g.AddEdge('e', 'f', 10);
g.AddEdge('f', 'g', 2);
g.AddEdge('g', 'h', 1);
g.AddEdge('g', 'i', 6);
g.AddEdge('h', 'i', 7);
graph<char, int> kminTree;
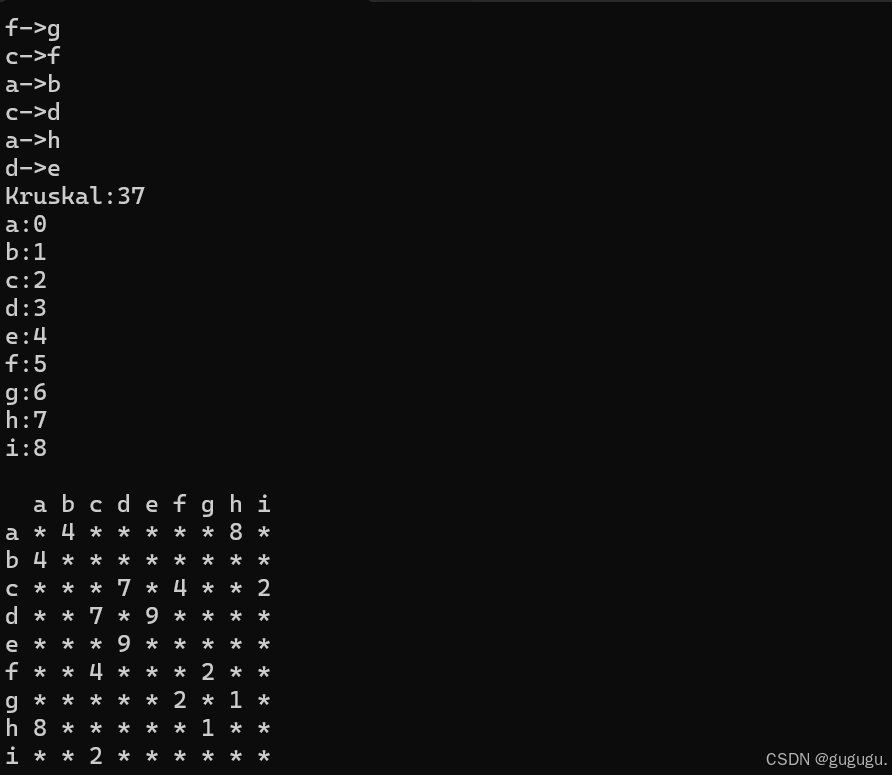
cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
kminTree.Print();
/*graph<char, int> pminTree;
cout << "Prim:" << g.Prim(pminTree, 'a') << endl;
pminTree.Print();
cout << endl;*/
/*for (size_t i = 0; i < strlen(str); ++i)
{
cout << "Prim:" << g.Prim(pminTree, str[i]) << endl;
}*/
}
测试的图以及中间的步骤
测试结果
Prim算法
Prim算法采用的是局部贪心的策略
怎么个事呢?
Prim算法原理
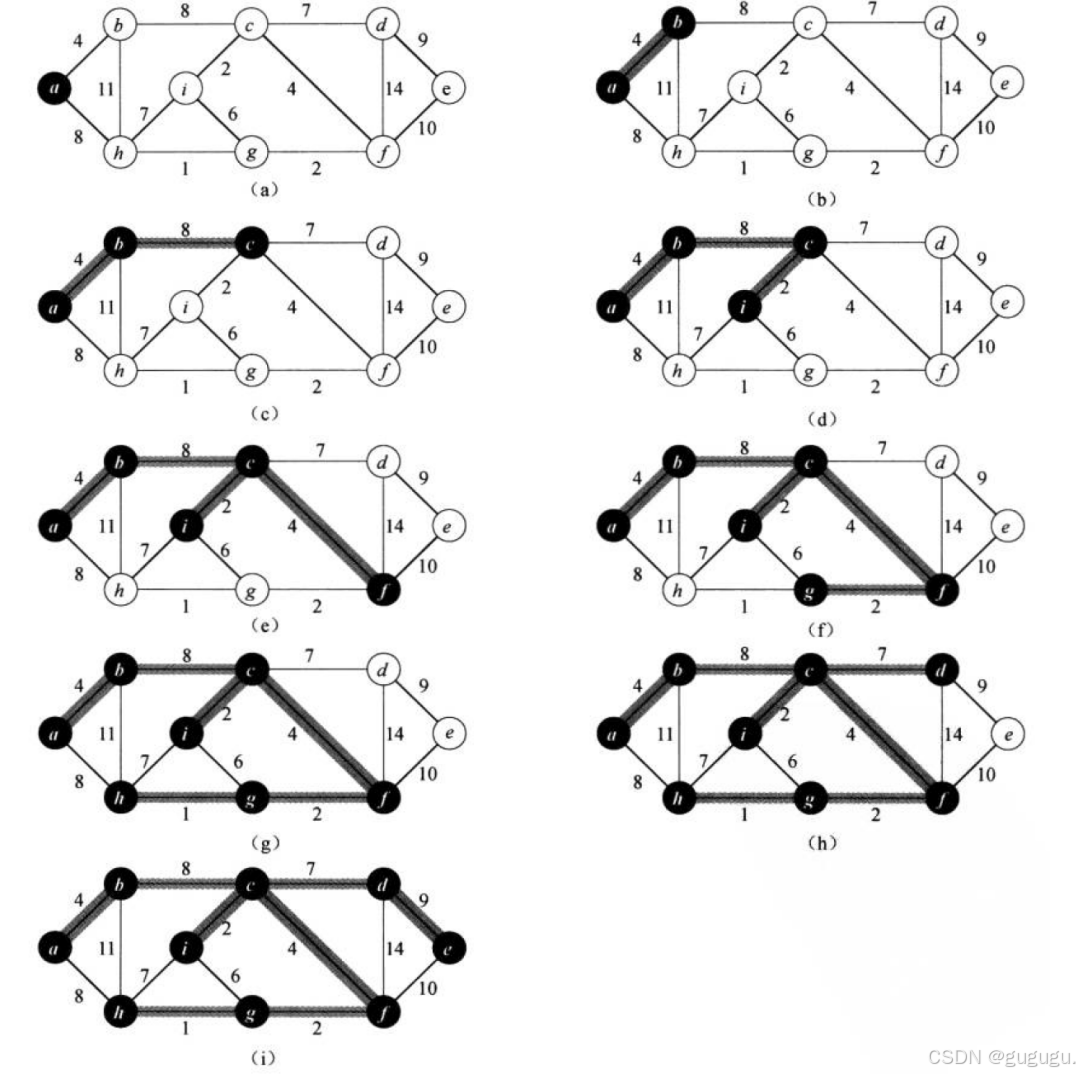
Prim算法需要两个集合
一个起点集合,一个终点集合
每次从起点集合和终点集合中分别选一个点,
这两个点之间构成的边需要是这两个集合中所能构成的边中最短的边。
说到起点集合,所以,Prim算法和Kruskal算法的一个区别就是,Prim算法需要指定起点
所以,这样我们每次所取得的边也是最小的。
而且这有一个好处,就是,我们不需要去判断是否成环,天然的避免了环的形成。
非常的精巧。
但是呢,又有新的问题来了,
难道我每一次都要去比较,去选出当前最短边吗?那岂不是太麻烦了
诶,每次都要选最短边,那不是小堆吗?
和Kruskal算法一样,也需要借助优先队列。
借助了优先队列,所以就也需要判判环了(还是要判环)
如何判环呢?
我们每次取的边,起点在一定是在起点集合,所以,我们只需要判断一下终点在不在起点集合就行了,比Kruskal算法的判环简单太多了。(哈哈哈)
首先,我们把起点相连的边进入优先队列,
然后每次取出堆顶元素,判断一下成不成环
如果成环,就跳过
如果不成环,就在新图中添加边,并且把终点作为新的起点,把与终点相连的边放进优先队列,同时,起点进入起点集合(注意,起点集合在最初一定是空的)
直到优先队列为空结束
当然最后,也需要像Kruskal算法一样,判断一下,最小生成树是否存在。
这一步骤和Kruskal算法相同
Prim算法我感觉是没有讲清楚,读者们,加油啊,得靠你们自己理解了
Prim算法代码
W Prim(Self& g, const V& src)
{
g._vertexs = _vertexs;
g._indexMap = _indexMap;
g._weights.resize(_vertexs.size());
for (int i = 0; i < _vertexs.size(); ++i)
{
(g._weights[i]).resize(_vertexs.size(), MAX_W);
}
W total = 0;
int EdgeSize = 0;
set<int> x;
int srci = getindex(src);
x.insert(srci);
priority_queue<Edge, vector<Edge>, greater<Edge>> pq;
for (int i = 0; i < _vertexs.size(); ++i)
{
if (x.count(i) == 0 && _weights[srci][i] != MAX_W)
pq.push(Edge(srci, i, _weights[srci][i]));
}
while (!pq.empty())
{
Edge front = pq.top();
pq.pop();
if (x.count(front._dsti) == 0)
{
g.AddEdge(_vertexs[front._srci], _vertexs[front._dsti], front._w);
cout << _vertexs[front._srci] << "->" << _vertexs[front._dsti] << endl;
total += front._w;
EdgeSize++;
x.insert(front._dsti);
for (int i = 0; i < _vertexs.size(); ++i)
{
if (x.count(i) == 0 && _weights[front._dsti][i] != MAX_W)
{
pq.push(Edge(front._dsti, i, _weights[front._dsti][i]));
}
}
}
}
if (EdgeSize == _vertexs.size() - 1)
return total;
return W();
}
代码演示
测试代码
void TestGraphMinTree()
{
const char* str = "abcdefghi";
graph<char, int> g(str, strlen(str));
g.AddEdge('a', 'b', 4);
g.AddEdge('a', 'h', 8);
//g.AddEdge('a', 'h', 9);
g.AddEdge('b', 'c', 8);
g.AddEdge('b', 'h', 11);
g.AddEdge('c', 'i', 2);
g.AddEdge('c', 'f', 4);
g.AddEdge('c', 'd', 7);
g.AddEdge('d', 'f', 14);
g.AddEdge('d', 'e', 9);
g.AddEdge('e', 'f', 10);
g.AddEdge('f', 'g', 2);
g.AddEdge('g', 'h', 1);
g.AddEdge('g', 'i', 6);
g.AddEdge('h', 'i', 7);
/*graph<char, int> kminTree;
cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
kminTree.Print();*/
graph<char, int> pminTree;
cout << "Prim:" << g.Prim(pminTree, 'a') << endl;
pminTree.Print();
cout << endl;
/*for (size_t i = 0; i < strlen(str); ++i)
{
cout << "Prim:" << g.Prim(pminTree, str[i]) << endl;
}*/
}
测试的图以及中间的步骤
测试结果