一、总体情况
- 这次考试一共有五道题
- 考试总共有3个小时,我花了一个多小时AC了 A A A, B B B, C C C 三道题,而 D D D 和 E E E 最后实在没想出来
二、题解
A题 被2的n次方整除
题目描述
给定一个正整数数组 a 1 , a 2 . . . a n a_{1}, a_{2}...a_{n} a1,a2...an。
使数组中所有数字的乘积(即 a 1 ∗ a 2 ∗ . . . ∗ a n a_{1} * a_{2} * ... * a_{n} a1∗a2∗...∗an)能被 2𝑛 整除。
你可以执行以下操作任意次数:
选择任意索引
i
i
i
(
1
≤
i
≤
n
)
(1 ≤ i ≤ n)
(1≤i≤n) 并将值 𝑎𝑖 替换为
a
i
=
a
i
∗
i
a_i = a_i * i
ai=ai∗i
不能重复对单个索引应用操作。换句话说,所有选择的
i
i
i 的值必须不同。
找到使数组中所有元素的乘积能被 2 n 2^n 2n 整除所需执行的最小操作次数。请注意,并非总是存在这样一组操作。
思路分析
这道题就是让我们尽量通过最小的操作次数,让所有数的乘积能被 2 n 2^{n} 2n 整除,换句话说,就是要让序列中所有的数一共尽可能有 n n n 个因数 2 2 2。知道了这点后,我们可以先把题目所给数组中的因数 2 2 2 的个数统计出来,再把每个 i i i 中的因数 2 2 2 的个数统计出来,再把每个 i i i 中的因数 2 2 2 的个数从大到小排序后,枚举即可。
代码
#include <iostream>
#include <vector>
#include <algorithm>
#define int long long
using namespace std;
const int N = 2e5 + 5;
int t;
int n;
int a[N];
vector<int> tmp;
bool cmp(int a, int b) {
return a > b;
}
void init() {
fill(a, a + N, 0);
tmp.clear();
}
int count(int x) {
int res = 0;
while (x > 0) {
if (x % 2 == 0)
res++;
else
break;
x /= 2;
}
return res;
}
main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> t;
while (t-- > 0) {
init();
cin >> n;
int k = n; //让序列里面尽量出现k个2
int cnt = 0; //记录因数2出现的数量,若>=k,则输出答案
int ans = 0; //操作次数(答案)
for (int i = 1; i <= n; i++) {
cin >> a[i];
cnt += count(a[i]);
if (count(i) != 0) {
tmp.push_back(count(i));
}
}
sort(tmp.begin(), tmp.end(), cmp);
int flag = false;
for (int i = 0; i < tmp.size(); i++) {
if (cnt >= k) {
cout << ans << '\n';
flag = true;
break;
}
cnt += tmp[i];
ans++;
}
if (!flag)
if (cnt >= k)
cout << ans << '\n';
else
cout << -1 << '\n';
}
return 0;
}
B题 资料分发
题目描述
有一些电脑,一部分电脑有双向数据线连接。如果一个电脑得到数据,它可以传送到的电脑都可以得到数据。现在,你有这个数据,问你至少将其输入几台电脑,才能使所有电脑得到数据。
思路分析
看到这道题后,很容易就想到了用并查集来维护这些电脑间的连通性关系,最后统计并查集的fa数组中一共有几个不同的值,就是答案。
代码
#include <iostream>
#include <set>
using namespace std;
const int N = 1e5 + 5;
int n, m;
int fa[N];
set<int> st;
int find(int u)
{
return fa[u] == u ? u : fa[u] = find(fa[u]);
}
int main()
{
ios::sync_with_stdio(false);
for (int i = 0; i < N; i++)
fa[i] = i;
cin >> n >> m;
int u, v;
for (int i = 1; i <= m; i++) {
cin >> u >> v;
fa[find(u)] = find(v);
}
int ans = 0;
for (int i = 1; i <= n; i++)
if (st.count(find(i)) == 0) {
ans++;
st.insert(find(i));
}
cout << ans << '\n';
return 0;
}
C题 统计和
题目描述
给定一个长度为 n ( n ≤ 1 0 5 ) n(n ≤ 10^{5}) n(n≤105),初始值都为 0 0 0 的序列, x ( x ≤ 1 0 5 ) x(x ≤ 10^{5}) x(x≤105) 次的修改某些位置上的数字,每次加上一个数,然后提出 y ( y ≤ 1 0 5 ) y(y ≤ 10^{5}) y(y≤105) 个问题,求每段区间的和。
思路分析
这道题是典型的的单点修改+区间查询,直接使用树状数组即可。
代码
#include <iostream>
#define int long long
using namespace std;
const int N = 1e5 + 5;
int n, m;
int tree[N];
int lowbit(int x)
{
return x & -x;
}
void modify(int idx, int c)
{
for (int i = idx; i <= n; i += lowbit(i))
tree[i] += c;
}
int query(int idx)
{
int res = 0;
for (int i = idx; i > 0; i -= lowbit(i))
res += tree[i];
return res;
}
main()
{
ios::sync_with_stdio(false);
cin >> n >> m;
char op;
int a, b;
for (int i = 1; i <= m; i++) {
cin >> op >> a >> b;
if (op == 'x')
modify(a, b);
else
cout << query(b) - query(a - 1) << '\n';
}
return 0;
}
D题 水火串
通过了光明狮子的考验,小渡来到了创界山的第二层。没想到第二层的守护神——火焰凤凰正沉迷于字母游戏,不能自拔!为了尽快得到她的帮助,小渡决定出手帮她解决字母游戏的谜题。 字母游戏规则是这样的:
一个字母串里包含有两个相邻的重复子串则称为“水串”,否则为“火串”
例如AA、ABCABC都是"水串",而D、DC、ABDAD、CBABCBA都是“火串"。
输入正整数L和n,输出由前L个字母组成的、字典序第n个的"火串"。
思路分析
这道题保证了字符串的长度最大为 80 80 80,则可以直接使用暴力法 DFS 求解,但在每次 DFS 时要加一个 check 函数判断新的这个串是不是火串,判断方法如下:
设一个要检查的字符串为"ACBABCABC",则检查过程如下:
因为每次DFS是往后加一个元素,所以要判断的重复子串中的其中一个的右端点一定是最后一个 (图中标*的元素)。然后去枚举另一个子串的右端点 (图中标.的元素),每次就以这两个右端点来暴力判断即可。
另外,这道题的输出限制非常严格,每一行的行尾甚至不能有空格,否则就很容易喜提 PE。
代码
#include <string>
#include <iostream>
#define s now
using namespace std;
int n, l;
int idx = 0;
string now;
bool check()
{
if (s.size() == 1)
return true;
int last = s.size() - 1;
for (int i = last - 1; i >= (int)(s.size() - 1) / 2; i--)
if (s[i] == s[last]) {
string t1 = "";
string t2 = "";
for (int j = i, k = last; j >= 0 && k > i; j--, k--) {
t1 += s[j];
t2 += s[k];
}
if (t1 == t2)
return false;
}
return true;
}
void output()
{
int t1 = 0;
int t2 = 0;
for (auto it = s.begin(); it != s.end(); it++) {
cout << *it;
t1++, t2++;
if (t2 == 64) {
cout << '\n';
t2 = 0, t1 = 0;
} else if (t1 == 4 && it != s.end() - 1) {
cout << ' ';
t1 = 0;
}
}
if (t2 == 0)
cout << s.size() << '\n';
else
cout << '\n' << s.size() << '\n';
}
void dfs()
{
if (idx > n)
return;
if (idx == n) {
output();
return;
}
for (int i = 0; i < l; i++) {
char tmp = 'A' + i;
now.push_back(tmp);
if (check()) {
idx++;
dfs();
}
now.pop_back();
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
while (cin >> n >> l && n && l) {
now = "";
idx = 0;
dfs();
}
return 0;
}
E题 过河
题目描述
在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点: 0 , 1 , ⋯ , L 0,1,\cdots,L 0,1,⋯,L(其中 L L L 是桥的长度)。坐标为 0 0 0 的点表示桥的起点,坐标为 L L L 的点表示桥的终点。青蛙从桥的起点开始,不停的向终点方向跳跃。一次跳跃的距离是 S S S 到 T T T 之间的任意正整数(包括 S , T S,T S,T)。当青蛙跳到或跳过坐标为 L L L 的点时,就算青蛙已经跳出了独木桥。
题目给出独木桥的长度 L L L,青蛙跳跃的距离范围 S , T S,T S,T,桥上石子的位置。你的任务是确定青蛙要想过河,最少需要踩到的石子数。
输入格式
输入共三行,
- 第一行有 1 1 1 个正整数 L L L,表示独木桥的长度。
- 第二行有 3 3 3 个正整数 S , T , M S,T,M S,T,M,分别表示青蛙一次跳跃的最小距离,最大距离及桥上石子的个数。
- 第三行有 M M M 个不同的正整数分别表示这 M M M 个石子在数轴上的位置(数据保证桥的起点和终点处没有石子)。所有相邻的整数之间用一个空格隔开。
输出格式
一个整数,表示青蛙过河最少需要踩到的石子数。
2
数据范围
- 对于 30 % 30\% 30% 的数据, 1 ≤ L ≤ 1 0 4 1\le L \le 10^4 1≤L≤104;
- 对于 100 % 100\% 100% 的数据, 1 ≤ L ≤ 1 0 9 1\le L \le 10^9 1≤L≤109, 1 ≤ S ≤ T ≤ 10 1\le S\le T\le10 1≤S≤T≤10, 1 ≤ M ≤ 100 1\le M\le100 1≤M≤100。
思路分析
这道题如果只看前 30 % 30\% 30% 的数据的话很容易就可以想到动态规划。设 f [ i ] f[i] f[i] 表示走到 i i i 这个位置时最小的石子数,则可以退出状态转移方程:
- 当 i i i 的位置没有石子时,则 f [ i ] = m i n ( f [ i − t + 1 ] , f [ i − t + 2 ] . . . f [ i − s + 1 ] ) f[i] = min(f[i - t + 1], f[i - t + 2]...f[i - s + 1]) f[i]=min(f[i−t+1],f[i−t+2]...f[i−s+1])
- 当 i i i 的位置有石子时,则 f [ i ] = m i n ( f [ i − t + 1 ] , f [ i − t + 1 ] . . . f [ i − s + 1 ] ) + 1 f[i] = min(f[i - t + 1], f[i - t + 1]...f[i - s + 1]) + 1 f[i]=min(f[i−t+1],f[i−t+1]...f[i−s+1])+1
但是,我们发现, L L L 的最大值是 1 0 9 10^9 109,但 S S S, T T T, M M M 都很小,可以考虑该怎么把每两个点间的距离压缩。
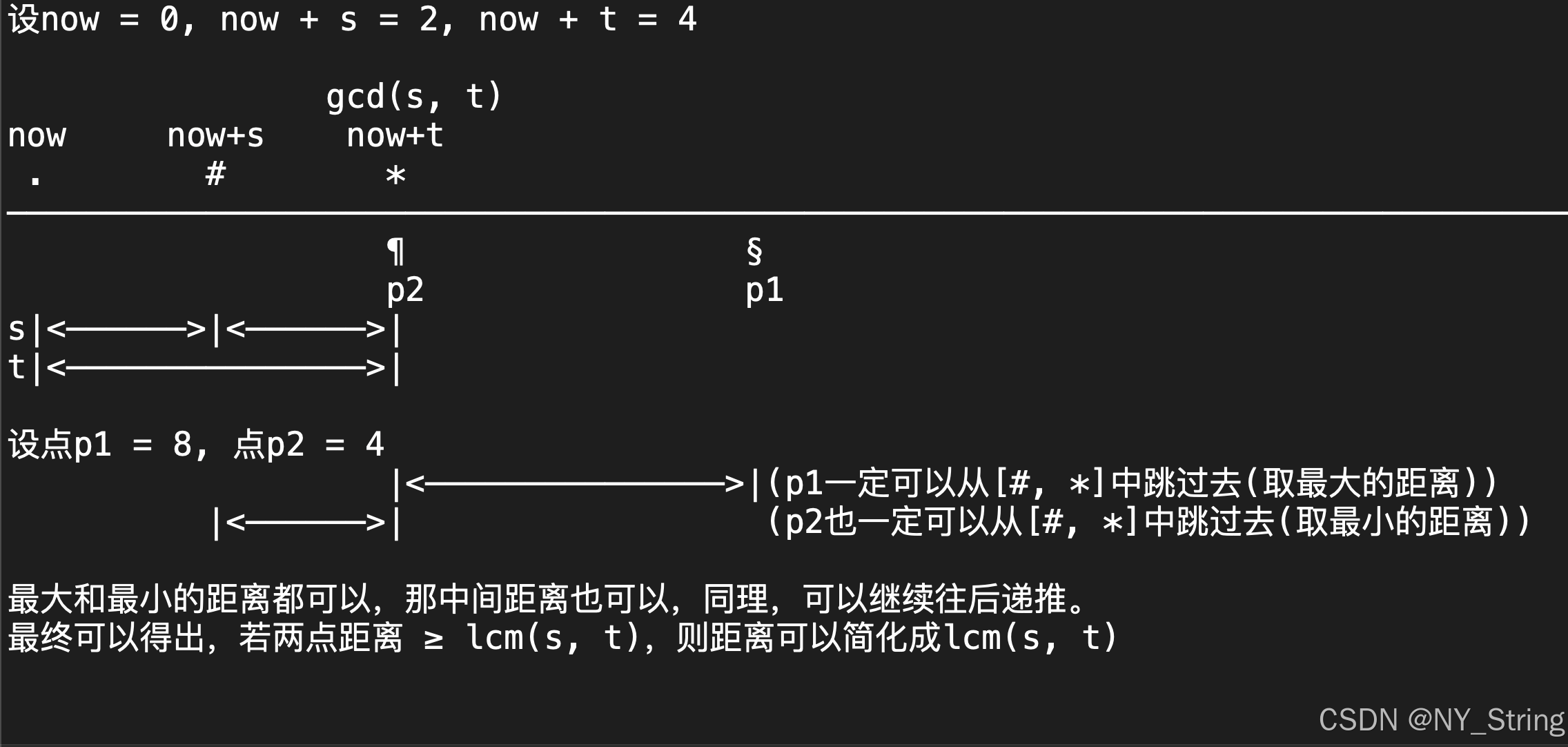
设每一步最小距离为 s s s,最大距离为 t t t,则可以证出:任何距离 ≥ ≥ ≥ l c m ( s , t ) lcm(s, t) lcm(s,t) 的点都可以走到,证明如下:
当对路径做完压缩后,就可以用动态规划求解。
代码
#include <iostream>
#include <map>
#include <algorithm>
#define rank _
#define INF 0x3f3f3f3f
using namespace std;
const int N = 105;
int l;
int s, t, m;
int rock[N];
int d[N];
int rank[N];
int f[10005];
map<int, bool> has_rock;
int gcd(int a, int b)
{
return b == 0 ? a : gcd(b, a % b);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> l >> s >> t >> m;
int min_distance = s * t / gcd(s, t);
for (int i = 1; i <= m; i++)
cin >> rock[i];
sort(rock + 1, rock + m + 1);
if (s == t) {
int ans = 0;
for (int i = 1; i <= m; i++)
if (rock[i] % s == 0)
ans++;
cout << ans << '\n';
return 0;
}
for (int i = 1; i <= m; i++) {
rank[i] = rank[i - 1] + min(rock[i] - rock[i - 1], min_distance);
has_rock[rank[i]] = true;
}
l = min(l - rank[m], min_distance) + rank[m];
for (int i = 1; i <= l; i++) {
int tmp = INF;
for (int j = s; j <= t; j++)
if (i - j >= 0)
tmp = min(tmp, f[i - j]);
if (has_rock[i])
f[i] = tmp + 1;
else
f[i] = tmp;
}
int ans = INF;
for (int i = l - t + 1; i <= l - s + 1; i++)
ans = min(ans, f[i]);
cout << ans << '\n';
return 0;
}
三、存在的不足
这次考试时简单题很快就全部AC了,而且AC后还有足够的时间,当时那两道难题我就一直在推,但没有思路,更没想怎么写代码。这导致了这次考试纯靠暴力电风扇DFS就能过的
D
D
D 题,代码都没写。
四、下次考试的改进措施
- 对于一些很明显暴力就能做的题,先想暴力做法,然后一定要写一遍代码,说不定就过了。但这并不等于说没思路就盲目开写,这么做的前提是这道题有很大希望是暴力都能过的,并且还有充足的时间来写代码。