激光SLAM总结——LIO-Mapping / LIOM / LINS / LIO-SAM算法解析

在激光SLAM领域，LOAM、Lego-LOAM属于纯激光领域，除此之外还衍生处理视觉激光结合、激光IMU结合，甚至三者结合的算法，视觉激光结合的算法在我之前写的博文激光SLAM总结——VLOAM / LIMO算法解析中有简单总结，本文所介绍的LIO-Mapping / LIOM / LINS / LIO-SAM算法就隶属于激光IMU结合的算法，在发展成熟度上面是要优于视觉激光融合的。

因为我是先学习的视觉SLAM算法，从整体框架上理解，LIOM、LINS类似于MSCKF，后端是基于滤波的方法实现两种传感器的紧耦合，而LIO-Mapping类似于VINS-Mono，后端是基于优化的方法实现两种传感器的紧耦合，LIO-SAM后端是基于因子图实现的多种传感器的紧耦合，对MSCKF和VINS-Mono不了解的同学可以如下参考博客：
VINS-Mono关键知识点总结——前端详解
VINS-Mono关键知识点总结——边缘化marginalization理论和代码详解
VINS-Mono关键知识点总结——预积分和后端优化IMU部分

学习MSCKF笔记——前端、图像金字塔光流、Two Point Ransac
学习MSCKF笔记——四元数基础
学习MSCKF笔记——真实状态、标称状态、误差状态
学习MSCKF笔记——后端、状态预测、状态扩增、状态更新
本篇博客，我对以上算法进行简单总结。

1. LIO-Mapping

LIO-Mapping是2019年发表于ICRA一篇论文，原论文为《Tightly Coupled 3D Lidar Inertial Odometry and Mapping》，主要是借鉴LOAM和VINS-Mono的思想进行联合状态估计，工程层面和VINS-Mono一样，只不过是前端视觉部分换成了Lidar的前端进行特征关联，这是第一篇开源的Lidar-IMU紧耦合SLAM算法，具体介绍如下：

1.1 总体框架

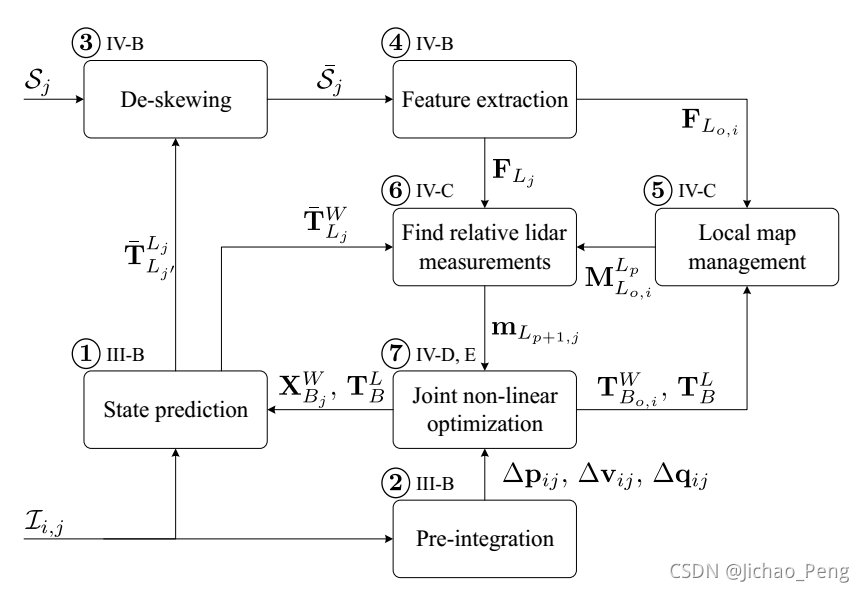
LIO-Mapping总体框架如下：

具体步骤如下：

1. 在激光雷达数据$S_j$到来之前，IMU原始输入${\mathcal{I}}_{i,j}$进行积分（State prediction）和预积分（Pre-intergration），积分的目的是为了获得我们需要估计的状态变量${\mathbf{p}}_{B_i}^W$，${\mathbf{v}}_{B_i}^W$和${\mathbf{q}}_{B_i}^W$，而预积分的目的是为了获得用于联合优化的$\Delta {\mathbf{p}}_{ij}$，$\Delta {\mathbf{v}}_{ij}$和$\Delta {\mathbf{q}}_{ij}$；
2. 当系统收到激光雷达数据$S_j$后，对激光雷达进行去畸变操作（De-skewing）获得去畸变点云$S_j$，然后在此基础上对去畸变点云提取激光雷达特征点${\mathbf{F}}_{L_j}$（Feature extraction）；
3. 在滑动窗口内的激光雷达特征${\mathbf{F}}_{L_{o,i}}$根据优化后的位姿${\mathbf{T}}_{B_{o,i}}^W$和${\mathbf{T}}_B^L$组成局部地图${\mathbf{M}}_{L_{o,i}}^{L_p}$（Local map management），根据预测的位姿实现当前帧激光特征点和局部地图的匹配（FInd relative lidar measurements）；
4. 最后就是激光雷达观测${\mathbf{m}}_{L_{p+1,j}}$以及预积分结果$\Delta {\mathbf{p}}_{ij}$，$\Delta {\mathbf{v}}_{ij}$和$\Delta {\mathbf{q}}_{ij}$实现联合优化，优化后的结果用于跟新IMU积分获得的状态变量，避免IMU漂移；

由于激光雷达去畸变及特征提取、预积分、边缘化等操作在VINS-Mono的相关博客中都有详细介绍，因此本篇博客只对LIO-Mapping中较为特殊的滑窗管理和地图注册进行总结

1.2 滑窗管理

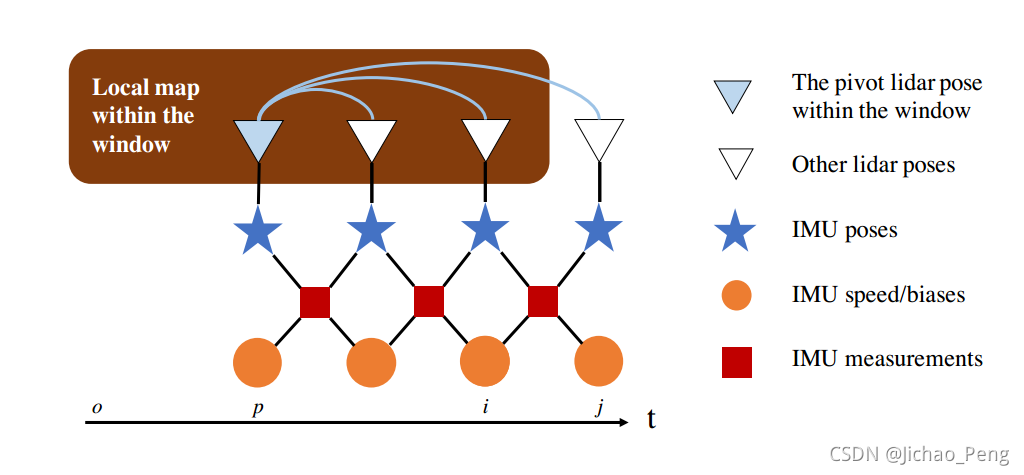
LIO-Mapping中滑窗管理示意图如下：

其中，$o$是滑窗中的第一帧Lidar Sweep，$i$是滑窗中最后一帧Lidar Sweep，$j$是当前帧的Lidar Sweep，$p$是滑窗中的Pivot Lidar Sweep，所谓Pivot Lidar Sweep指的就是整个滑窗内帧的位姿都是基于该帧坐标系建立的，随着滑窗移动，Pivot Lidar Sweep也不断变化。

我们将滑窗内的特征点构建为局部地图 M L o , i L p = F L γ L p , γ ∈ { o , … , i } \mathbf{M}_{L_{o}, i}^{L_{p}} = \mathbf{F}_{L_{\gamma}}^{L_{p}}, \gamma \in\{o, \ldots, i\} MLo​,iLp​​=FLγ​Lp​​,γ∈{o,…,i}，然后我们通过KNN算法找到原始特征点 F L α , α ∈ { p + 1 , … , j } \mathbf{F}_{L_{\alpha}}, \alpha \in\{p+1, \ldots, j\} FLα​​,α∈{p+1,…,j}与局部地图的对应关系并构建点到面的残差，优化过程中会优化窗口中所有帧相对Pivot Lidar Sweep的相对位姿以${\mathbf{T}}_{L_{\alpha }}^{L_p}$及包括Pivot Lidar Sweep的位姿${\mathbf{T}}_{L_p}^W$，而其中相对位姿可以表示为：$${\mathbf{T}}_{L_{\alpha }}^{L_p}={\mathbf{T}}_B^L{\mathbf{T}}_{B_p}^W{}^{-1}{\mathbf{T}}_{B_{\alpha }}^W{\mathbf{T}}_B^{L-1}=\left[\begin{array}{cc}{\mathbf{R}}_{L_{\alpha }}^{L_p}& {\mathbf{p}}_{L_{\alpha }}^{L_p}\\ 0& 1\end{array}\right]$$那么激光雷达的点到面的残差可以表示为：$${\mathbf{r}}_{\mathcal{L}}\left(m,{\mathbf{T}}_{L_p}^W,{\mathbf{T}}_{L_{\alpha }}^W,{\mathbf{T}}_B^L\right)={\mathbf{\omega }}^T\left({\mathbf{R}}_{L_{\alpha }}^{L_p}x+{\mathbf{p}}_{L_{\alpha }}^{L_p}\right)+d$$结合边缘化残差和预积分残差，整个优化的代码函数为 min ⁡ X 1 2 { ∥ r P ( X ) ∥ 2 + ∑ m ∈ m L α α ∈ { p + 1 , ⋯   , j } ∥ r L ( m , X ) ∥ C L α m 2 + ∑ β ∈ { p , ⋯   , j − 1 } ∥ r B ( z β + 1 β , X ) ∥ C B β + 1 B β 2 } \begin{array}{c} \min _{\mathbf{X}} \frac{1}{2}\left\{\left\|\mathbf{r}_{\mathcal{P}}(\mathbf{X})\right\|^{2}+\sum_{m \in \mathbf{m}_{L_{\alpha}} \atop \alpha \in\{p+1, \cdots, j\}}\left\|\mathbf{r}_{\mathcal{L}}(m, \mathbf{X})\right\|_{\mathbf{C}_{L_{\alpha}}^{m}}^{2}\right. \\ \left.+\sum_{\beta \in\{p, \cdots, j-1\}}\left\|\mathbf{r}_{\mathcal{B}}\left(z_{\beta+1}^{\beta}, \mathbf{X}\right)\right\|_{\mathbf{C}_{B_{\beta+1}}^{B_{\beta}}}^{2}\right\} \end{array} minX​21​{∥rP​(X)∥2+∑α∈{p+1,⋯,j}m∈mLα​​​​∥rL​(m,X)∥CLα​m​2​+∑β∈{p,⋯,j−1}​ ​rB​(zβ+1β​,X) ​CBβ+1​Bβ​​2​}​其中${\mathbf{r}}_{\mathcal{P}}(\mathbf{X})$是边缘化残差，${\mathbf{r}}_{\mathcal{L}}(m,\mathbf{X})$为激光雷达残差，${\mathbf{r}}_{\mathcal{B}}\left(z_{\beta +1}^{\beta },\mathbf{X}\right)$为预积分残差，优化变量为滑窗内的所有帧状态变量以及激光到车体的标定：$$\mathbf{X}=\left[{\mathbf{X}}_{B_p}^W,\dots ,{\mathbf{X}}_{B_j}^W,{\mathbf{T}}_B^L\right]$$其中$${\mathbf{X}}_{B_i}^W=[{\mathbf{p}}_{B_i}^{W^T}{\mathbf{v}}_{B_i}^{W^T}{\mathbf{q}}_{B_i}^{W^T}{\mathbf{b}}_{a_i}^T{\mathbf{b}}_{g_i}{}^T{]}^T$$$${\mathbf{T}}_B^L={\left[\begin{array}{ll}{\mathbf{p}}_B^{L^T}& {\mathbf{q}}_B^{L^T}\end{array}\right]}^T$$

1.3 地图注册

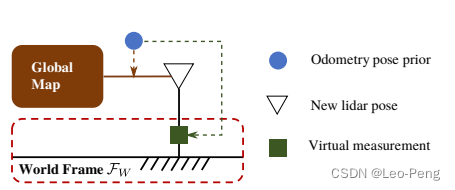
在优化获得位姿后，论文还有一步Refinement with Rotational Constraints的过程，就是将当前帧的激光雷达点对齐到全局地图中去，这也是为什么叫LIO-mapping的原因

对齐相关的损失函数建立如下：$${\mathbf{C}}_{\mathcal{M}}=\sum _{m\in {\mathbf{m}}_L}{\Vert {\mathbf{r}}_{\mathcal{M}}\left(m,{\mathbf{T}}_L^W\right)\Vert }^2，{\mathbf{r}}_{\mathcal{M}}(m,\mathbf{T})={\mathbf{\omega }}^T(\mathbf{Rx}+\mathbf{p})+d$$其中，${\mathbf{T}}_L^W$为前一步估计出来的激光位姿，$m$是激光测量，我们使用高斯牛顿法对上述损失函数进行求解。${\mathbf{J}}_{\mathrm{p}}^{\mathrm{C}}$和${\mathbf{J}}_{\theta }^{\mathrm{C}}$为残差相对位置和姿态的雅克比，为了保证地图和重力是对齐的，因此采用SE(2)-Constraint优化，由于Yaw方向姿态有更高的不确定性，而Roll和Pitch相对更加准确，因此通过旋转的雅克比进行修改来限制损失函数：$${\mathbf{J}}_{{\mathbf{\theta }}_z}^{\mathbf{C}}={\mathbf{J}}_{\mathbf{\theta }}^{\mathbf{C}}\cdot (\breve{\mathbf{R}}{)}^T\cdot {\breve{\mathbf{\Omega }}}_z$$$${\breve{\Omega }}_z=\left[\begin{array}{ccc}{ϵ}_x& 0& 0\\ 0& {ϵ}_y& 0\\ 0& 0& 1\end{array}\right]$$其中，$\breve{(\cdot )}$为上一轮迭代估计的状态变量，${\breve{\Omega }}_z$是姿态相对与世界坐标系的信息矩阵的近似值，${ϵ}_x,{ϵ}_y$表示在世界系下$x$和$y$轴的旋转相对$z$轴的旋转的information ratio。在优化步骤中通过修改后的${\mathbf{J}}_{\mathbf{p}}^{\mathbf{C}}$和${\mathbf{J}}_{{\mathbf{\theta }}_z}^{\mathbf{C}}$计算增量$\delta {\theta }_z$和$\delta \mathbf{p}$，然后再进行状态更新$$\tilde{\mathbf{p}}=\breve{\mathbf{p}}+\delta \mathbf{p}$$$$\tilde{\mathbf{q}}=\left[\begin{array}{c}\frac{1}{2}\delta {\mathbf{\theta }}_z\\ 1\end{array}\right]\otimes \breve{\mathbf{q}}$$

1.4 实验结果

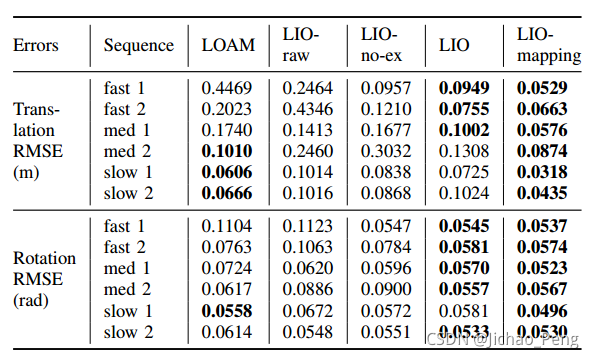
如下是对比和消融实验：

LIO-raw指的是不对激光雷达进行运动补偿的结果，LIO-no-ex值得是没有进行在线外参估计的方法，LIO是带有滑窗优化的方法，LIO-mapping是带有Rotation Constraints的方法，从结果看，LIO-mapping效果确实更好。如下是个模块计算耗时：

由于Odometry和Mapping是在不同的线程中，系统整体上可以做到按照IMU输出进行运行。

2. LIOM

LIOM是2019年发表于IROS的一篇文章，该文章原标题为《A Robust Laser-Inertial Odometry and Mapping Method for Large-Scale Highway Environments》，论文强调要解决的是高速场景的激光定位问题，高速场景的主要挑战在于速度快、缺乏几何特征、运动物体多、回环少等，而本文的主要贡献是分割网络去除动态物体的影响同时引入激光惯性框架进行高速环境下的运动估计，具体如下：

2.1 总体框架

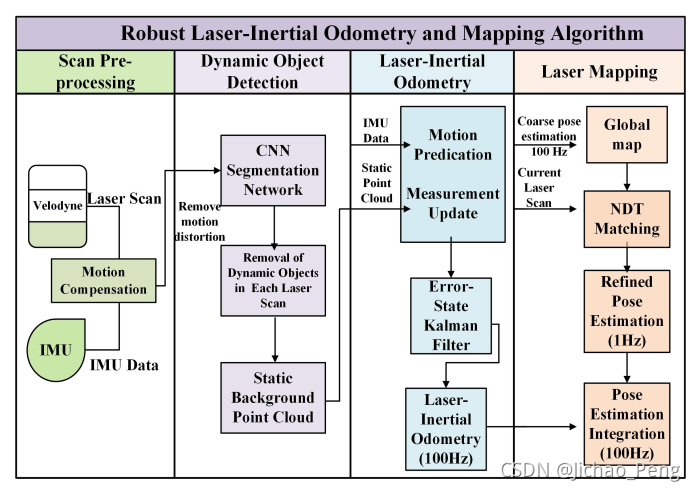
LIOM算法总体框架如下：

如上图所示，算法由四个模块组成，

1. Scan Pre-process模块负责进行激光点云去畸变操作；
2. Dynamic Object Detection模块负责通过语义分割进行动态物体检测；
3. Laser-Inertial Odometry模块使用误差状态卡尔曼滤波来融合激光和IMU数据以高频输出位姿估计；
4. Laser Mapping模块负责建立全局地图，然后使用当前帧激光点云和全局地图进行匹配来实现定位结果的Refinement。

这里，我们简单回顾下基于误差状态的扩展卡尔曼滤波流程：

2.1 激光点云去畸变

在高速场景下对激光点云去畸变是非常有必要的，其步骤如下：

1. 对每一帧的所有激光点都标记时间戳：$$t_{\text{curr }}=t_{\text{start }}+\partial \times \frac{{\theta }_{\text{curr }}}{{\theta }_{\text{end }}}(1)$$其中$\partial$是激光帧的扫描周期
2. 找到时间戳$k$到$k+1$的连续IMU测量，其中$k$取最接近当前激光点时间戳$t_{\text{curr }}$的IMU测量
3. 获得IMU在时刻$k$和$k+1$在世界坐标系中的位姿$$T_k^w=\left[p_x,p_y,p_z,v_x,v_y,v_z,{\theta }_x,{\theta }_y,{\theta }_z\right]$$$$T_{k+1}^w=\left[p_x,p_y,p_z,v_x,v_y,v_z,{\theta }_x,{\theta }_x,{\theta }_z\right]$$
4. 使用线性插值确定IMU在时刻$t_{\text{curr }}$在世界坐标系中的位姿：$${\text{ ratio }}_{\text{front }}=\frac{t_{\text{curr }}-t_k}{t_{k+1}-t_k}$$$${\text{ ratio }}_{\text{back }}=\frac{t_{k+1}-t_{\text{curr }}}{t_{k+1}-t_k}$$$$T_{\text{curr }}^w=T_{k+1}^w\times {\text{ ratio }}_{\text{front }}+T_k^w\times {\text{ ratio }}_{\text{back }}$$
5. 通过当前激光点和当前激光帧起始点的位置$P_{\text{curr }}^w,P_{\text{start }}^w$和速度$V_{\text{curr }}^w,V_{\text{start }}^w$可以获得在当前激光帧起始点坐标系下的运动扰动$\Delta P_{\text{curr }}^{\text{start }}$：$$\Delta P_{\mathrm{curr}}^w=P_{\mathrm{curr}}^w-\left(P_{\mathrm{start}}^w+V_{\mathrm{start}}^w\times \partial \times \frac{{\theta }_{\text{curr }}}{{\theta }_{\text{end }}}\right)$$$$\Delta P_{\text{curr }}^{\text{start }}=R_w^{\text{start }}\Delta P_{\text{curr }}^w$$
6. 变换开始点坐标系下的所有激光点，对每个激光点提取他们的运动扰动$\Delta P_{\text{curr }}^{\text{siart }}$

2.3 误差状态扩展卡尔曼滤波

1. 状态变量定义：
   在误差状态扩展卡尔曼滤波中要区分真实状态$x$，标称状态$\hat{x}$和误差状态$\mathbf{\delta }x$的区别，他们的关系如下：$$x=\hat{x}\oplus \mathbf{\delta }x$$LIOM中没有对外参进行在线估计（MSCKF中有），因此误差状态变量相对简单，如下：$$\delta x=\left[\begin{array}{c}\delta v\\ \delta p\\ \delta \theta \\ \delta a_b\\ \delta w_b\end{array}\right]$$其中$a_b$ 和 $w_b$是加速度计和陀螺仪偏置

2. 传播过程：
   传播过程包含预测状态传播和误差协方差传播，其中预测状态传播基于标称状态通过欧拉积分获得，如下：$$\left[\begin{array}{c}{\hat{v}}_{t+1}\\ {\hat{p}}_{t+1}\\ {\hat{R}}_{t+1}\\ {\hat{a}}_{b(t+1)}\\ {\hat{w}}_{b(t+1)}\end{array}\right]=\left[\begin{array}{c}{\hat{v}}_t+\left[{\hat{R}}_t\left(a_m-{\hat{a}}_{b(t)}\right)+g\right]\Delta t\\ {\hat{p}}_t+{\hat{v}}_t\Delta t+\frac{1}{2}\left[{\hat{R}}_t\left(a_m-{\hat{a}}_{b(t)}\right)+g\right]\Delta t^2\\ {\hat{R}}_{t}R\left\{\left(w_m-{\hat{w}}_{b(t)}\right)\Delta t\right\}\\ {\hat{a}}_{b(t)}\\ {\hat{w}}_{b(t)}\end{array}\right]$$误差状态的协方差传播需要根据误差状态变量运动方程线性化后获得，误差状态变量微分方程如下：$$\delta \dot{x}=\left[\begin{array}{c}\delta \dot{v}\\ \delta \dot{p}\\ \delta \dot{\theta }\\ \delta {\dot{a}}_b\\ \delta {\dot{w}}_b\end{array}\right]=\left[\begin{array}{c}-\hat{R}{\left[a_m-{\hat{a}}_b\right]}_{\times }\delta \theta -\hat{R}\delta a_b-{\eta }_a\\ \delta v\\ -{\left[w_m-{\hat{w}}_b\right]}_{\times }\delta \theta -\delta w_b-{\eta }_w\\ {\eta }_a\\ {\eta }_w\end{array}\right]$$那么误差状态运动学方程可以写为： [ δ v t + 1 δ p t + 1 δ R t + 1 δ a b ( t + 1 ) δ w b ( t + 1 ) ] = [ δ v t + ( − R ^ t [ a m − a ^ b ] × δ θ − R ^ t δ a b ) Δ t + η v δ p t + δ v t Δ t R { − ( w m − w ^ b ) Δ t } δ θ − δ w b Δ t − η θ δ a b ( t ) + η a δ w b ( t ) + η w ] \left[\begin{array}{c} \delta{v}_{t+1} \\ \delta{p}_{t+1} \\ \delta{R}_{t+1} \\ \delta{a}_{b(t+1)} \\ \delta{w}_{b(t+1)} \end{array}\right]=\left[\begin{array}{c} \delta{v}_{t}+(-\hat{R}_{t}\left[a_{m}-\hat{a}_{b}\right]_{\times} \delta \theta-\hat{R}_{t} \delta a_{b}) \Delta t + {\eta}_v \\ \delta{p}_{t}+\delta{v}_{t} \Delta t\\ R\{-(w_{m}-\hat{w}_{b}) \Delta t \} \delta \theta - \delta w_{b} \Delta t - {\eta}_\theta\\ \delta{a}_{b(t)} + \eta_{a} \\ \delta{w}_{b(t)} + \eta_{w} \end{array}\right] ​δvt+1​δpt+1​δRt+1​δab(t+1)​δwb(t+1)​​ ​= ​δvt​+(−R^t​[am​−a^b​]×​δθ−R^t​δab​)Δt+ηv​δpt​+δvt​ΔtR{−(wm​−w^b​)Δt}δθ−δwb​Δt−ηθ​δab(t)​+ηa​δwb(t)​+ηw​​ ​以上运动学方程可以表示为：$$\delta \mathbf{x}={\mathbf{F}}_{\mathbf{x}}\delta \mathbf{x}+{\mathbf{F}}_{\mathbf{n}}\mathbf{w}，\mathbf{w}\sim \mathcal{N}(0,\mathbf{Q})$$其中 F x = [ 0 I 3 − R ^ t [ a m − a ^ b ] × Δ t − R ^ t Δ t 0 I 3 I 3 Δ t 0 0 0 0 0 R { − ( w m − w ^ b ) Δ t } ) 0 − I 3 Δ t 0 0 0 I 3 0 0 0 0 0 I 3 ] \mathbf{F}_{\mathbf{x}}=\left[\begin{array}{cccccc} \mathbf{0} & I_{3} & -\hat{R}_{t}\left[a_{m}-\hat{a}_{b}\right]_{\times} \Delta t & -\hat{R}_{t} \Delta t & \mathbf{0}\\ I_{3} & I_{3} \Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0}\\ \mathbf{0} & \mathbf{0} &R\{-(w_{m}-\hat{w}_{b}) \Delta t \} ) & \mathbf{0} & -I_{3}\Delta t \\ \mathbf{0} & \mathbf{0} & \mathbf{0} &I_{3} & \mathbf{0}\\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & I_{3} \end{array}\right] Fx​= ​0I3​000​I3​I3​Δt000​−R^t​[am​−a^b​]×​Δt0R{−(wm​−w^b​)Δt})00​−R^t​Δt00I3​0​00−I3​Δt0I3​​ ​$${\mathbf{F}}_{\mathbf{i}}=\left[\begin{array}{cccc}{I}_3& 0& 0& 0\\ 0& 0& 0& 0\\ 0& I_3& 0& 0\\ 0& 0& I_3& 0\\ 0& 0& 0& I_3\end{array}\right]$$$$\mathbf{Q}=\mathrm{diag}\left(\mathrm{Cov}\left({\mathbf{\eta }}_v\right),0_3,\mathrm{Cov}\left({\mathbf{\eta }}_{\mathbf{\theta }}\right),\mathrm{Cov}\left({\mathbf{\eta }}_g\right),\mathrm{Cov}\left({\mathbf{\eta }}_a\right)\right)$$误差状态的均值和协方差的预测如下：
   $$\delta {\mathbf{x}}_{\text{pred }}=\mathbf{F}\delta \mathbf{x}$$$${\bar{\Sigma }}_{t+1}={\mathbf{F}}_x{\Sigma }_t{\mathbf{F}}_x^T+{\mathbf{F}}_n{Q}_n{\mathbf{F}}_n^T$$其中我们并不关心误差状态的均值部分，因为在ESKF的每次更新后误差状态的均值就会被重置，而协方差部分则可以指导整个误差估计的分布情况。

3. 更新过程：
   观测模型如下：$$\delta y=H\delta x=\left[\begin{array}{ccccc}0& I_3& 0& 0& 0\\ 0& 0& I_3& 0& 0\end{array}\right]\delta x$$通过预测过程，我们可以获得一个先验的状态变量及方差$\delta {\bar{x}}_{t+1}^m\in {\mathbb{R}}^6,{\bar{\Sigma }}_{t+1}^m\in {\mathbb{R}}^{6\times 6}$，根据先验的状态变量及方差，基于NDT算法，我们可以获得后验状态变量及方差$\delta x_{t+1}^m\in {\mathbb{R}}^6$ , ${\Sigma }_{t+1}^m\in {\mathbb{R}}^{6\times 6}$，根据先验和后验的误差，我们就可以计算出观测以及观测误差的大小：$$C_{t+1}^m={\left(({\Sigma }_{t+1}^m{)}^{-1}-{\left({\bar{\Sigma }}_{t+1}^m\right)}^{-1}\right)}^{-1}$$$$\delta y_{t+1}^m={\left(K^m\right)}^{-1}\left(\delta x_{t+1}^m-\delta {\bar{x}}_{t+1}^m\right)+\delta {\bar{x}}_{t+1}^m$$其中$K^m={\bar{\Sigma }}_{t+1}{H}^{mT}{\left(H^m{\bar{\Sigma }}_{t+1}{H}^{mT}+C_{t+1}^m\right)}^{-1}\in {\mathbb{R}}^{6\times 6}$，这一步称为inversing the kalman filter measurement update，有了观测之后，我们就可以进行正常的卡尔曼更新了，如下：$$K={\bar{\Sigma }}_{t+1}{H}^T{\left(H{\bar{\Sigma }}_{t+1}{H}^T+C_{t+1}\right)}^{-1}$$$$\delta x_{t+1}=K\left(\delta y_{t+1}-H\delta {\bar{x}}_{t+1}\right)$$$${\Sigma }_{t+1}=\left(I_{15}-KH\right){\bar{\Sigma }}_{t+1}$$最后进行误差矫正即可，如下：$$\left[\begin{array}{c}{\hat{v}}_{t+1}\\ {\hat{p}}_{t+1}\\ {\hat{R}}_{t+1}\\ {\hat{a}}_{b(t+1)}\\ {\hat{w}}_{b(t+1)}\end{array}\right]=\left[\begin{array}{c}{\hat{v}}_t+\delta v_{t+1}\\ {\hat{p}}_t+\delta p_{t+1}\\ {\hat{R}}_t\cdot R\left(\delta {\theta }_{t+1}\right)\\ {\hat{a}}_{bt}+\delta a_{b(t+1)}\\ {\hat{w}}_{bt}+\delta w_{b(t+1)}\end{array}\right]$$关于上述inversing the kalman filter measurement update我其实不太理解，为什么NDT算法获得后验状态变量和卡尔曼更新中观测需要通过一个新的卡尔曼增益进行转换？如果有读者对这部分有更加深入的理解可以评论补充

2.2 实验结果

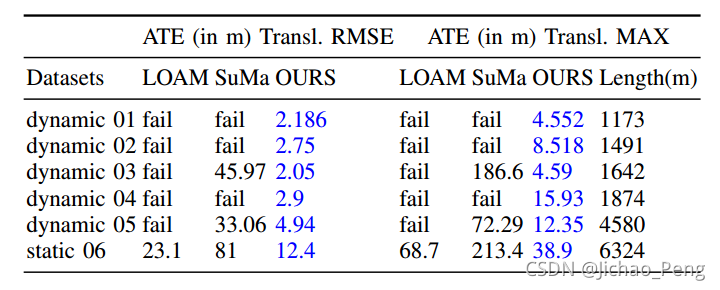
在论文中，作者在高速公路数据集上对比了LIOM，LOAM和SuMa三种算法的结果，LIOM的鲁棒性明显提高，如下所示：

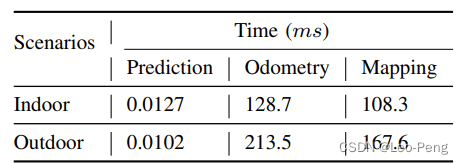
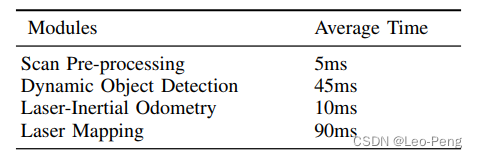
各个模块耗时如下：

和LIO-Mapping对比，基于滤波的Odometry和Mapping都会有明显的速度优势

3 . LINS

LINS是2020年发表于ICRA上的一篇文章，原论文名称为《LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation》，该论文的主要特点在于使用了基于误差状态的迭代扩展卡尔曼滤波，并且以机器人中心重新定义了状态变量，论文还和LIO-Mapping进行了对比，在精度相同的情况下取得了更高的效率。

3.1 总体框架

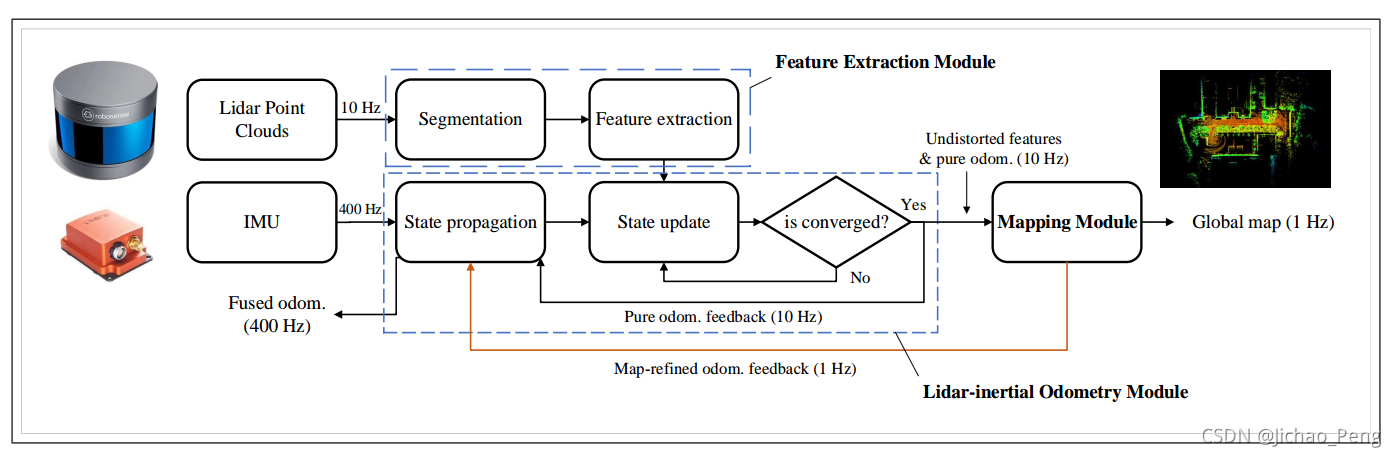
算法总体框架如下：

算法整体框架也是非常清晰明了，Feature Extraction Module主要用于提取激光雷达特征点，Lidar-inertial Odometry Module就是通过卡尔曼滤波融合激光雷达特征点和IMU，Mapping Module主要利用全局地图来Refine里程计的结果。Feature Extraction Module主要参考的LOAM和Lego-LOAM算法，这里我们主要总结其中核心的基于误差状态的迭代卡尔曼滤波。

3.2 误差状态扩展卡尔曼滤波

LINS中的误差状态扩展卡尔曼滤波的特点主要是：

1. 以机器人中心定义的状态变量，避免了在线性化过程中不断增大的不确定性；
2. 使用迭代扩展卡尔曼滤波，以取得更高的精度；

下面具体展开，在LIOM算法中，所有状态变量都是建立在世界坐标系下，并对其进行拓展卡尔曼滤波，这样由于线性化导致的误差是在不断累积的，但是在LINS，状态变量定义如下：$${\mathbf{x}}_w^{b_k}:=\left[{\mathbf{p}}_w^{b_k},{\mathbf{q}}_w^{b_k}\right]$$$${\mathbf{x}}_{b_{k+1}}^{b_k}:=\left[{\mathbf{p}}_{b_{k+1}}^{b_k},{\mathbf{v}}_{b_{k+1}}^{b_k},{\mathbf{q}}_{b_{k+1}}^{b_k},{\mathbf{b}}_a,{\mathbf{b}}_g,{\mathbf{g}}^{b_k}\right]$$其中${\mathbf{p}}_{b_{k+1}}^{b_k}$和${\mathbf{q}}_{b_{k+1}}^{b_k}$为世界系相对于$b_k$帧坐标系的旋转和平移，${\mathbf{p}}_{b_{k+1}}^{b_k}$和${\mathbf{q}}_{b_{k+1}}^{b_k}$从$b_{k+1}$帧到$b_k$帧的旋转平移变化在$b_k$帧下的表达，${\mathbf{v}}_{b_{k+1}}^{b_k}$在${\mathbf{g}}_{b_{k+1}}^{b_k}$为在$b_k$帧下的速度和重力加速度，所谓“以机器人中心定义状态变量”指的就是参与迭代扩展卡尔曼滤波是${\mathbf{x}}_{b_{k+1}}^{b_k}$，而${\mathbf{x}}_w^{b_k}$是根据${\mathbf{x}}_{b_{k+1}}^{b_k}$的滤波结果进行更新，本身不参与滤波，因此可以避免线性化过程误差的累计。
${\mathbf{x}}_{b_{k+1}}^{b_k}$的误差状态变量定义如下$$\mathbf{\delta }\mathbf{x}:=\left[\mathbf{\delta }\mathbf{p},\delta \mathbf{v},\delta \theta ,\delta {\mathbf{b}}_a,\delta {\mathbf{b}}_g,\delta \mathbf{g}\right]$$误差状态$\delta \mathbf{x}$、标称状态${}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}$与真实状态${\mathbf{x}}_{b_{k+1}}^{b_k}$关系如下$${\mathbf{x}}_{b_{k+1}}^{b_k}={}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}\text{ 田 }\mathbf{\delta }\mathbf{x}=\left[\begin{array}{c}{}^{-}{\mathbf{p}}_{b_{k+1}}^{b_k}+\delta \mathbf{p}\\ {}^{-}{\mathbf{v}}_{b_{k+1}}^{b_k}+\mathbf{\delta }\mathbf{v}\\ {}^{-}{\mathbf{q}}_{b_{k+1}}^{b_k}\otimes \exp (\mathbf{\delta }\theta )\\ {}^{-}{\mathbf{b}}_a+\mathbf{\delta }{\mathbf{b}}_a\\ {}^{-}{\mathbf{b}}_g+\mathbf{\delta }{\mathbf{b}}_g\\ {}^{-}{\mathbf{g}}^{b_k}+\mathbf{\delta }\mathbf{g}\end{array}\right]$$误差状态的线性连续时间运动模型如下：$$\delta \dot{\mathbf{x}}(t)={\mathbf{F}}_t\delta \mathbf{x}(t)+{\mathbf{G}}_t\mathbf{w}$$其中噪声项$\mathbf{w}={\left[{\mathbf{n}}_a^T,{\mathbf{n}}_g^T,{\mathbf{n}}_{b_a}^T,{\mathbf{n}}_{b_g}^T\right]}^T$，系数矩阵分别为：$${\mathbf{F}}_t=\left[\begin{array}{cccccc}0& \mathbf{I}& 0& 0& 0& 0\\ 0& 0& -{\mathbf{R}}_t^{b_k}{\left[{\hat{\mathbf{a}}}_t\right]}_{\times }& -{\mathbf{R}}_t^{b_k}& 0& 0\\ 0& 0& -{\left[{\hat{\omega }}_t\right]}_{\times }& 0& -{\mathbf{I}}_3& -{\mathbf{I}}_3\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$$${\mathbf{G}}_t=\left[\begin{array}{cccc}0& 0& 0& 0\\ -{\mathbf{R}}_t^{b_k}& 0& 0& 0\\ 0& -{\mathbf{I}}_3& 0& 0\\ 0& 0& {\mathbf{I}}_3& 0\\ 0& 0& 0& {\mathbf{I}}_3\\ 0& 0& 0& 0\end{array}\right]$$其中${\hat{\mathbf{a}}}_t={\mathbf{a}}_{m_t}-{\mathbf{b}}_a$，${\hat{\omega }}_t={\omega }_{m_t}-{\mathbf{b}}_g$，接下来是对运动模型进行离散化，如下：$$\delta {\mathbf{x}}_{t_{\tau }}=\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right)\delta {\mathbf{x}}_{t_{\tau -1}}$$状态变量方差递推如下：$${\mathbf{P}}_{t_{\tau }}=\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right){\mathbf{P}}_{t_{\tau -1}}{\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right)}^T+\left({\mathbf{G}}_{t\tau }\Delta t\right)\mathbf{Q}{\left({\mathbf{G}}_{t_{\tau }}\Delta t\right)}^T$$其中$\Delta t=t_{\tau }-t_{\tau -1}$，而$t_{\tau }$和$t_{\tau -1}$分别是IMU的连续两个时刻，$\mathbf{Q}$是噪声$\mathbf{w}$的矩阵表达。

在此基础上就可以对状态变量进行卡尔曼更新，在迭代卡尔曼滤波中，状态更新类似于优化问题，需要考虑构建一个残差，然后类似于优化一样在每一次迭代中取得不同的更新量，在LIOM中，设计的优化残差为$$\underset{\delta \mathbf{x}}{\min }\Vert \delta \mathbf{x}{\Vert }_{{\left({\mathbf{P}}_k\right)}^{-1}}+\Vert f\left({}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}\text{ 田 }\mathbf{\delta }\mathbf{x}\right){\Vert }_{{\left({\mathbf{J}}_k{\mathbf{M}}_{\mathbf{k}}{\mathbf{J}}_k^T\right)}^{-1}}$$从中看出优化目标是使得误差状态最小同时观察误差最小，其中$\Vert \cdot \Vert$为$M$范数，${\mathbf{J}}_k$为函数$f(\cdot )$相对测量噪声的的雅克比，而${\mathbf{M}}_k$为测量噪声矩阵，函数$f(\cdot )$为$$f_i\left({\mathbf{x}}_{b_{k+1}}^{b_k}\right)=\{\begin{array}{cl}\frac{\left|\left({\hat{\mathbf{p}}}_i^{l_k}-{\mathbf{p}}_a^{l_k}\right)\times \left({\hat{\mathbf{p}}}_i^{l_k}-{\mathbf{p}}_b^{I_k}\right)\right|}{\left|{\mathbf{p}}_a^{l_k}-{\mathbf{p}}_b^{l_k}\right|}& \text{ if }{\mathbf{p}}_i^{l_{k+1}}\in {\mathbb{F}}_e\\ \frac{\left|{\left({\hat{\mathbf{p}}}_i^k-{\mathbf{p}}_a^l\right)}^T\left(\left({\mathbf{p}}_a^k-{\mathbf{p}}_b^k\right)\times \left({\mathbf{p}}_a^l-{\mathbf{p}}_c^l\right)\right)\right|}{\left|\left({\mathbf{p}}_a^{l_k}-{\mathbf{p}}_b^{l_k}\right)\times \left({\mathbf{p}}_a^{l_k}-{\mathbf{p}}_c^{l_c}\right)\right|}& \text{ if }{\mathbf{p}}_i^{l_{k+1}}\in {\mathbb{F}}_p\end{array}$$其中${\hat{\mathbf{p}}}_i^{l_k}$是${\mathbf{p}}_i^{l_{k+1}}$通过状态变量变换到当前帧的特征点，如下：$${\hat{\mathbf{p}}}_i^{l_k}={\mathbf{R}}_l^{b^T}\left({\mathbf{R}}_{b_{k+1}}^{b_k}\left({\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right)+{\mathbf{p}}_{b_{k+1}}^{b_k}-{\mathbf{p}}_l^b\right)$$如果熟悉LOAM或者Lego-LOAM算法的同学应该知道，这个就是LOAM或者Lego-LOAM算法中求解位姿构建的点到线和点到面的残差，在此就不再赘述。通过求解残差，我们可以获得迭代更新公式：$${\mathbf{K}}_{k,j}={\mathbf{P}}_k{\mathbf{H}}_{k,j}^T{\left({\mathbf{H}}_{k,j}{\mathbf{P}}_k{\mathbf{H}}_{k,j}^T+{\mathbf{J}}_{k,j}{\mathbf{M}}_k{\mathbf{J}}_{k,j}^T\right)}^{-1}$$$$\Delta {\mathbf{x}}_j={\mathbf{K}}_{k,j}\left({\mathbf{H}}_{k,j}\mathbf{\delta }{\mathbf{x}}_j-f\left({}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}\text{ 田 }\delta {\mathbf{x}}_j\right)\right)$$$$\delta {\mathbf{x}}_{j+1}=\delta {\mathbf{x}}_j+\Delta {\mathbf{x}}_j$$其中${\mathbf{H}}_{k,j}$为$f\left(-{\mathbf{x}}_{b_{k+1}}^{b_k}\text{ 田 }\mathbf{\delta }{\mathbf{x}}_j\right)$相对$\delta {\mathbf{x}}_j$的雅克比，在这一步中特征点的残差参与到了卡尔曼滤波的过程中，因此本文是一种紧耦合方法。在每次迭代过程中，算法都会寻找新的匹配边界点和面点，并计算新的${\mathbf{H}}_{k,j}$、${\mathbf{J}}_{k,j}$和${\mathbf{K}}_{k,j}$，当$f\left({\mathbf{x}}_{b_{k+1}}^{b_k}\right)$小于一定阈值或者达到n次迭代后，我们就可以更新状态变量的残差：$${\mathbf{P}}_{k+1}=\left(\mathbf{I}-{\mathbf{K}}_{k,n}{\mathbf{H}}_{k,n}\right){\mathbf{P}}_k{\left(\mathbf{I}-{\mathbf{K}}_{k,n}{\mathbf{H}}_{k,n}\right)}^T+{\mathbf{K}}_{k,n}{\mathbf{M}}_k{\mathbf{K}}_{k,n}^T$$最后，我们初始化下一阶段${\mathbf{x}}_{b_{k+2}}^{b_{k+1}}$为：$$\left[0_3,{\mathbf{v}}_{b_{k+1}}^{b_{k+1}},{\mathbf{q}}_0,{\mathbf{b}}_a,{\mathbf{b}}_g,{\mathbf{g}}^{b_{k+1}}\right]$$其中，${\mathbf{q}}_0$为单位旋转，${\mathbf{v}}_{b_{k+1}}^{b_{k+1}}={\mathbf{R}}_{b_k}^{b_{k+1}}{\mathbf{v}}_{b_{k+1}}^{b_k}$，${\mathbf{g}}^{b_{k+1}}={\mathbf{R}}_{b_k}^{b_{k+1}}{\mathbf{g}}^{b_k}$

当获得${\mathbf{x}}_{b_{k+1}}^{b_k}$后我们就可以更新世界系相对于$b_{k+1}$帧坐标系的旋转和平移，其实也就是$b_{k+1}$帧在世界系下的位姿：$${\mathbf{x}}_w^{b_{k+1}}=\left[\begin{array}{l}{\mathbf{p}}_w^{b_{k+1}}\\ {\mathbf{q}}_w^{b_{k+1}}\end{array}\right]=\left[\begin{array}{c}{\mathbf{R}}_{b_k}^{b_{k+1}}\left({\mathbf{p}}_w^{b_k}-{\mathbf{p}}_{b_{k+1}}^{b_k}\right)\\ {\mathbf{q}}_{b_k}^{b_{k+1}}\otimes {\mathbf{q}}_w^{b_k}\end{array}\right]$$

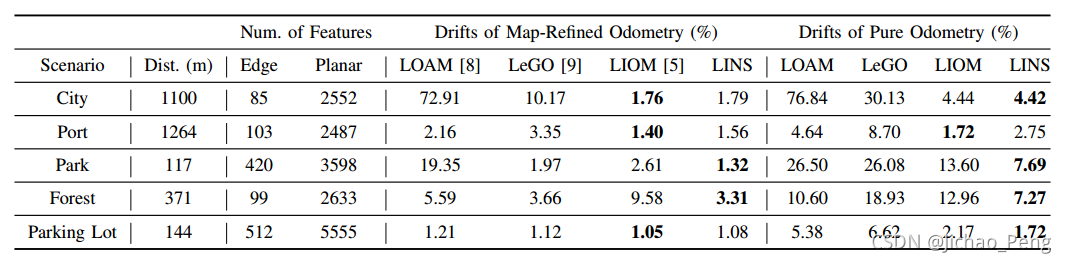
3.3 实验结果

LINS的实验结果如下：

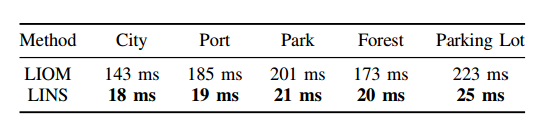
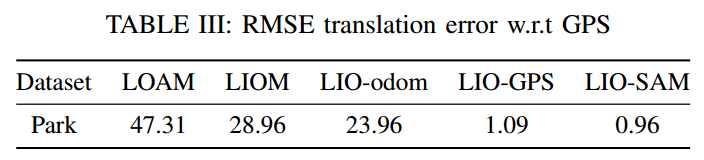
注意这里的LIOM指的是《Tightly Coupled 3D Lidar Inertial Odometry and Mapping》中提出的基于优化的方法，从上表中可以看出，LINS精度和LIOM是相当的，但是在下表计算时间的对比中，LINS的优势就非常明显（注意这里对比的LIOM指的是《Tightly Coupled 3D Lidar Inertial Odometry and Mapping》这篇文章）。
在LIOM中最耗时的部分是需要2D约束维护一个Local Map并且基于MAP Estimation通过 Scan to Map的匹配进行状态变量求解，而LINS使用了迭代卡尔曼滤波替代了MAP Estimation，相当于降低了优化问题的维度，并且使用的是Scan to Scan的匹配，因此速度得到了较大的提升。

这里我们可以来简单理一下LIOM、LINS和MSCKF中滤波状态的区别：
三者相同点都是误差状态，都是根据IMU进行运动方程进行预测，根据激光后者视觉观测进行更新，不同点是LIOM是最基本的误差状态扩展卡尔曼滤波，状态变量中直接包括最终要估计的位姿，而LINS在滤波的状态变量中不包括最终要估计的位姿，而是前后帧相对运动结果，在MSCKF中的状态变量中除了IMU当前时刻的位姿还包括历史的相机状态，IMU相关的状态变量方差在预测过程中预测，而相机相关的状态变量的方差在扩增时预测，因此这三者是各有不同的。

4. LIO-SAM

4.1 总体框架

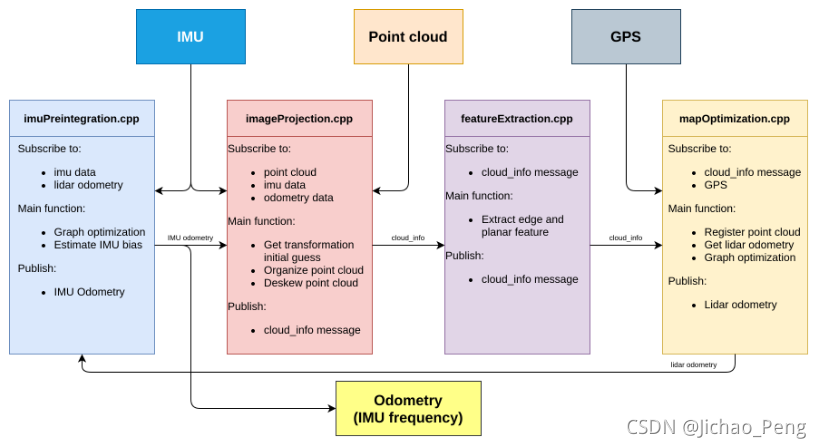
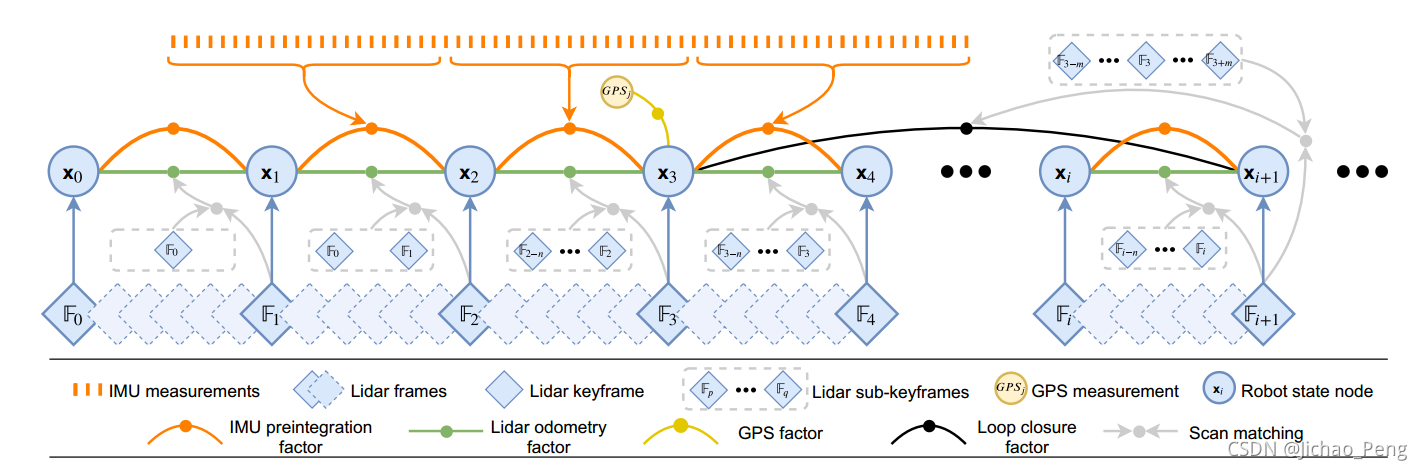
LIO-SAM总体框如下图所示

从图中可以看出来，IMU数据除了用来构建IMU预积分因子之外，还用来进行激光雷达去畸变操作，在IMU预积分完成后，在将IMU将里程计作为先验用来获取激光里程计，激光里程计除了进行Scan-to-Map的匹配之外，还构建一个包括激光雷达因子、GPS因子和回环因子的因子图，用来优化地图和激光里程计的结果，优化后的激光里程计的结果再传递回IMU预积分节点，构建IMU预积分因子图，包括激光里程计因子、IMU预分因子和IMU测量Bias的因子，在论文中给出的因子图如下（看起来是一个，实现起来其实是两个）：

因子图中包括IMU预积分因子、激光雷达里程计因子、GPS因子、回环因子。而我们要估计的状态变量为：$$\mathbf{x}={\left[{\mathbf{R}}^{\mathbf{T}},{\mathbf{p}}^{\mathbf{T}},{\mathbf{v}}^{\mathbf{T}},{\mathbf{b}}^{\mathbf{T}}\right]}^{\mathbf{T}}$$整个优化过程是建立在用于增量平滑的Bayers Tree上的，关于因子图基础知识、Bayers Tree、以及LIO-SAM中关于因子图构建的部分代码我都总结在GTSAM Tutorial学习笔记，下面我仅仅对LIO-SAM中各个因子的基本原理进行介绍。

4.2 因子图构建

在LIO-SAM的因子图中一个有四种因子，我们分别介绍
IMU预积分因子：
IMU从时刻$t$积分到$t+\Delta t$的公式为$${\mathbf{v}}_{t+\Delta t}={\mathbf{v}}_t+\mathbf{g}\Delta t+{\mathbf{R}}_t\left({\hat{\mathbf{a}}}_t-{\mathbf{b}}_t^{\mathbf{a}}-{\mathbf{n}}_t^{\mathbf{a}}\right)\Delta t$$$$\begin{array}{rl}{\mathbf{p}}_{t+\Delta t}={\mathbf{p}}_t& +{\mathbf{v}}_t\Delta t+\frac{1}{2}\mathbf{g}\Delta t^2+\frac{1}{2}{\mathbf{R}}_t\left({\hat{\mathbf{a}}}_t-{\mathbf{b}}_t^{\mathbf{a}}-{\mathbf{n}}_t^{\mathbf{a}}\right)\Delta t^2\end{array}$$$${\mathbf{R}}_{t+\Delta t}={\mathbf{R}}_t\exp \left(\left({\hat{\mathbf{\omega }}}_t-{\mathbf{b}}_t^{\mathbf{\omega }}-{\mathbf{n}}_t^{\mathbf{\omega }}\right)\Delta t\right)$$其中$${\hat{\mathbf{\omega }}}_t={\mathbf{\omega }}_t+{\mathbf{b}}_t^{\omega }+{\mathbf{n}}_t^{\omega }$$$${\hat{\mathbf{a}}}_t={\mathbf{R}}_t^{\mathrm{BW}}\left({\mathbf{a}}_t-\mathbf{g}\right)+{\mathbf{b}}_t^{\mathrm{a}}+{\mathbf{n}}_t^{\mathrm{a}}$$$${\mathbf{R}}_t={\mathbf{R}}_t^{\mathbf{WB}}={\mathbf{R}}_t^{\mathbf{B}{W}^{\top }}$$其中预积分测量值为：$$\Delta {\mathbf{v}}_{ij}={\mathbf{R}}_i^{\top }\left({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij}\right)$$$$\Delta {\mathbf{p}}_{ij}={\mathbf{R}}_i^{\top }\left({\mathbf{p}}_j-{\mathbf{p}}_i-{\mathbf{v}}_i\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2\right)$$$$\Delta {\mathbf{R}}_{ij}={\mathbf{R}}_i^{\top }{\mathbf{R}}_j$$从公式可以看出来，LIO-SAM中定义的预积分和我们在LIOM和VINS-Mono中定义预积分结果都不太一样，因为在LIO-SAM的代码实现中是直接是用GTSAM中自带的预积分类实现的，这个类中具体怎么实现预积分的还有待考证，除此之外，IMU Bias因子作为除IMU预积分因子之外单独的一部分参与联合优化。

激光里程计因子
激光里程计和LOAM的原理基本一样，但是区别是LIO-SAM中的构建了关键帧，地图也是利用关键中的特征点构建的局部地图 M i = { M i e , M i p } \mathbf{M}_{i}=\left\{\mathbf{M}_{i}^{e}, \mathbf{M}_{i}^{p}\right\} Mi​={Mie​,Mip​}其中$${\mathbf{M}}_i^e={}^{\prime }{\mathrm{F}}_i^e{\cup }^{\prime }{\mathrm{F}}_{i-1}^e\cup \dots {\cup }^{\prime }{\mathrm{F}}_{i-n}^e$$$${\mathbf{M}}_i^p={}^{\prime }{\mathrm{F}}_i^p{\cup }^{\prime }{\mathrm{F}}_{i-1}^p\cup \dots {\cup }^{\prime }{\mathrm{F}}_{i-n}^p$$然后是利用Scan-to-Map的原理进行计算的

GPS因子
当接收到GPS测量后，我们首先变换它们到笛卡尔坐标系中。当一个新的位姿节点被插入到因子图后，我们关联GPS因子到该位姿节点中去。具体地，我们线性插值GPS的时间戳，得到对应最新位姿节点的GPS位置。

由于在GPS信号一直存在的时候，持续添加GPS因子没有意义。因为漂移很缓慢。所以在实际操作过程中，我们只添加GPS因子当位姿估计协方差矩阵变得很大的时候。

这一部分原理介绍还是很简单的，因为因子图的构建基于GTSAM本来就很简介，LIO-SAM不太一样的地方其实是一种“半紧耦合”是解决方案，先获得IMU里程计和激光雷达里程计，然后通过因子图的方式将两者结合起来，没那么紧的融合方式效果也很好

4.3 实验结果

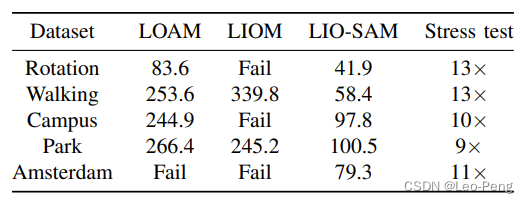
LIO-SAM的实验结果是非常惊艳的，如下图所示：

以及RMSE结果的对比如下：

耗时对比如下：

但是我在别人的博客里看到有同学提到，算法在自己平台上实现效果不是很好，算法我还没有自己跑起来过，之后有时间再测评下。

以上就是所有内容，有问题欢迎交流！

此外，对其他SLAM算法感兴趣的同学可以看考我的博客SLAM算法总结——经典SLAM算法框架总结