椋鸟数据结构笔记#5：树、二叉树基础

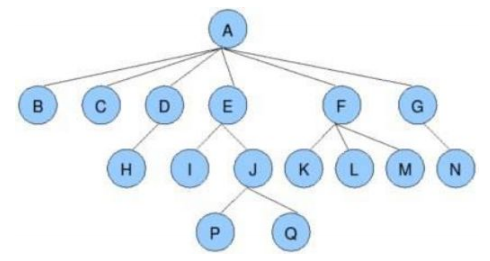
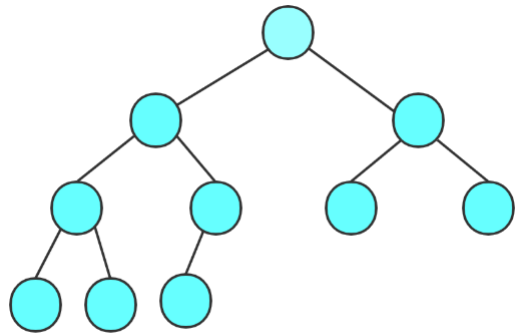
子节点（孩子节点）：与父节点相对，就是树中与某节点相连但在其“下方”的节点。比方说，上方示意图中BCDEFG都是A的子节点。
兄弟节点：有相同父节点的节点互为兄弟节点。比方说，上方示意图中B与C互为兄弟节点、P与Q互为兄弟节点。
堂兄弟节点：只要两个节点互不为兄弟节点但处于树的同一层（与根节点的距离相同，则称其为堂兄弟节点。比方说，上方示意图中H与J互为堂兄弟节点。
节点的祖先：一个节点到根节点的唯一路径上所有的节点都是该节点的祖先。比方说，上方示意图中A节点为所有节点的祖先。
节点的子孙：又某一个节点“向下”延伸出来的所有节点都是该节点的子孙。比方说，上方示意图中其他所有节点都是A节点的子孙。
子树：把根节点的一个子节点拿出来，这个节点与其所有子孙再次组成一棵树，这棵树就称为母树（原本的树）的一棵子树。比方说上方示意图中E、I、J、P、Q就构成了母树的一棵子树。注意子树可以只有一个根节点
节点的度：一个节点的子树的个数称为节点的度。比方说，上方示意图中A节点的度为6
树的度：一棵树最大的节点的度就是这棵树的度。比方说，上方示意图中树的度就是A节点的度，为6.
叶节点（终端节点）：度为0的节点（没有子节点）就是叶节点。比方说，上方示意图中BCHIKLMNPQ都是叶节点。
分支节点（非终端节点）：度不为0的节点（有子节点）就是分支节点。比方说，上方示意图中ADEFGJ都是分支节点。
森林：多颗不相连的树组成森林。

树的表示

树的表示方法有多种，这里介绍较为常用的左孩子右兄弟表示法。这个方法能够让我们方便的向下查找。

我们定义一个结构体作为树的节点：

typedef int TDataType	//树存储的数据类型

typedef struct Tree
{
	TDataType data;
    struct Tree\* lChild;
    struct Tree\* rSibling;
} Tree;

这个结构体中，lChild存储该节点最左边的子节点，rSibling存储与其紧邻的右侧兄弟节点。

这样，我们还是以上方示意图为例，为了方便我再次把图片贴出：

在这里插入图片描述

如果我们想通过A节点找到P节点，这时问题就会变的非常简单了，只需要按照如下路线图寻找即可：

#mermaid-svg-lK6KbPe1mE26fkBj {font-family:“trebuchet ms”,verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-lK6KbPe1mE26fkBj .error-icon{fill:#552222;}#mermaid-svg-lK6KbPe1mE26fkBj .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-lK6KbPe1mE26fkBj .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-lK6KbPe1mE26fkBj .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-lK6KbPe1mE26fkBj .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-lK6KbPe1mE26fkBj .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-lK6KbPe1mE26fkBj .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-lK6KbPe1mE26fkBj .marker{fill:#333333;stroke:#333333;}#mermaid-svg-lK6KbPe1mE26fkBj .marker.cross{stroke:#333333;}#mermaid-svg-lK6KbPe1mE26fkBj svg{font-family:“trebuchet ms”,verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-lK6KbPe1mE26fkBj .label{font-family:“trebuchet ms”,verdana,arial,sans-serif;color:#333;}#mermaid-svg-lK6KbPe1mE26fkBj .cluster-label text{fill:#333;}#mermaid-svg-lK6KbPe1mE26fkBj .cluster-label span{color:#333;}#mermaid-svg-lK6KbPe1mE26fkBj .label text,#mermaid-svg-lK6KbPe1mE26fkBj span{fill:#333;color:#333;}#mermaid-svg-lK6KbPe1mE26fkBj .node rect,#mermaid-svg-lK6KbPe1mE26fkBj .node circle,#mermaid-svg-lK6KbPe1mE26fkBj .node ellipse,#mermaid-svg-lK6KbPe1mE26fkBj .node polygon,#mermaid-svg-lK6KbPe1mE26fkBj .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-lK6KbPe1mE26fkBj .node .label{text-align:center;}#mermaid-svg-lK6KbPe1mE26fkBj .node.clickable{cursor:pointer;}#mermaid-svg-lK6KbPe1mE26fkBj .arrowheadPath{fill:#333333;}#mermaid-svg-lK6KbPe1mE26fkBj .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-lK6KbPe1mE26fkBj .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-lK6KbPe1mE26fkBj .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-lK6KbPe1mE26fkBj .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-lK6KbPe1mE26fkBj .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-lK6KbPe1mE26fkBj .cluster text{fill:#333;}#mermaid-svg-lK6KbPe1mE26fkBj .cluster span{color:#333;}#mermaid-svg-lK6KbPe1mE26fkBj div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:“trebuchet ms”,verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-lK6KbPe1mE26fkBj :root{–mermaid-font-family:“trebuchet ms”,verdana,arial,sans-serif;}

lChlid

rSibling*3

lChlid

rSibling

lChild

如果想要子节点也能向上寻找，那还可以再结构体中添加一个成员用于储存父节点。

二叉树基础

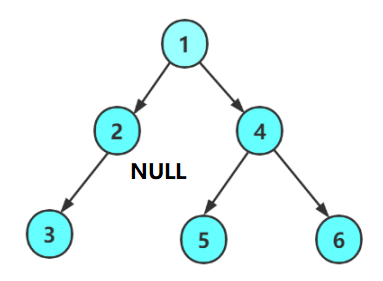
二叉树是一种特殊的树结构，其特征为每一个节点都有且只有两个子树或空子树。

下方是一个二叉树的示意图（其中2节点的右子树就是空）：

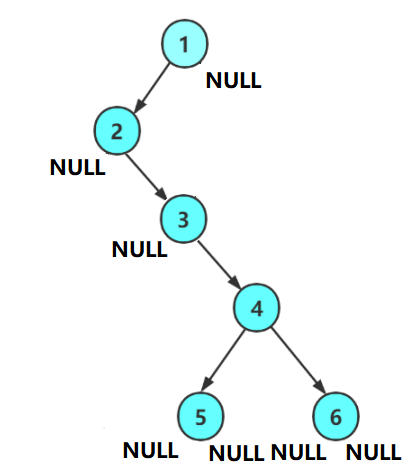
在这里插入图片描述

我们还可以更加抽象一点，下图同样也是一个二叉树：

在这里插入图片描述

二叉树分类

有两种特殊的二叉树类型需要我们单独的来看一看，它们是满二叉树和完全二叉树。

满二叉树

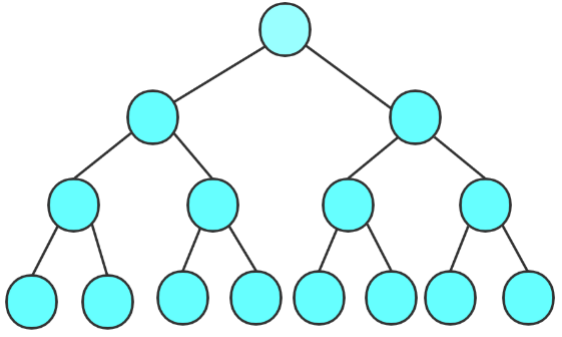
一个二叉树如果每一层的节点数都达到最大，那这就是一个满二叉树，一个 k 层的满二叉树的节点总数是 2k - 1 。

在这里插入图片描述

完全二叉树

完全二叉树的概念看图很好理解，但是用文字描述就比较复杂了。++对于深度为 K 的有 n 个节点的二叉树，当且仅当其每一个节点都与深度为 K 的满二叉树中编号从 1 至 n 的节点一一对应时称之为完全二叉树++{.wavy}。

在这里插入图片描述

二叉树的性质

一棵非空二叉树的第 i 层上最多有 2i-1 个节点。
深度为 h 的二叉树的最大节点数是 2h - 1 。
对任何一棵二叉树，若度为 0 的节点个数为 n0 ，度为 2 的节点个数为 n2 ，那么 n0 = n2 + 1 。
具有 n 个节点的满二叉树深度为 log2(n + 1) 。
若逐层从左至右给每一个节点编号（根节点编号0），那么对应序号为 i 的节点：
1. **i 的父节点的编号为
⌊

(

i

−

1

)

/

2

⌋

\lfloor (i-1)/2 \rfloor

⌊(i−1)/2⌋ （当

i

0

i>0

i>0时）**
2. **i 的左孩子节点编号为

2

i
1

2i+1

2i+1（当

2

i