原题链接

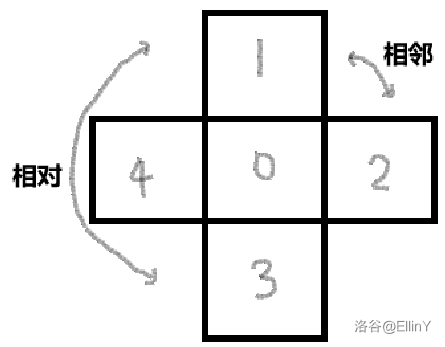
题目翻译中的错误及补充

输入格式

输入包含多组数据，每组数据占一行。一组数据中包含若干个以空格隔开的整数，以 $0$ 结尾。最后有一行一个单独的 $0$，表示数据输入完毕。

输出格式

对于每一组数据，输出一行表示答案。

样例输入

1 2 3 4 1 2 3 3 4 2 0
1 4 3 4 3 2 3 2 1 0
0

样例输出

22
18

箭头的布局应为：

思路

容易看出是 dp。用 d p i , j ( j ∈ { 0 , 1 , 2 , 3 , 4 } ) dp_{i,j}(j\in\{0,1,2,3,4\}) dpi,j​(j∈{0,1,2,3,4}) 表示到了第 $i$ 个箭头，除了踩在 $a_i$（箭头所示位置）上的脚之外另一只脚踩在 $j$ 的位置。转移时分类讨论（用 $i$ 更新 $i+1$）：

1. 踩在 $a_i$ 上的脚刚好在 $a_{i+1}$ 上，再踩一次，耗费 $1$ 点体力。
2. 踩在 $j$ 上的脚刚好在 $a_{i+1}$ 上，再踩一次，耗费 $1$ 点体力。
3. 移动踩在 $a_i$ 上的脚去踩 $a_{i+1}$。
4. 移动踩在 $j$ 上的脚去踩 $a_{i+1}$。

为了计算一个位置到另一个位置的体力耗费，我使用了 cal 函数计算，cal 同样要分类讨论：

1. 从 $0$ 到其他位置：$2$。
2. 从 $x$ 到 $x+1$ 或者从 $4$ 到 $1$，从 $1$ 到 $4$：$3$。
3. 其他情况：$4$。

转移方程：
$\{\begin{array}{l}d{p}_{i+1,j}=\min (d{p}_{i+1,j},d{p}_{i,j}+1)a_i=a_{i+1}\\ d{p}_{i+1,a_i}=\min (d{p}_{i+1,a_i},d{p}_{i,j}+1)j=a_{i+1}\\ d{p}_{i+1,j}=\min (d{p}_{i+1,j},d{p}_{i,j}+cal(a_i,a_{i+1})),d{p}_{i+1,a_i}=\min (d{p}_{i+1,a_i},d{p}_{i,j}+cal(j,a_{i+1}))a_i\ne a_{i+1}且j\ne a_{i+1}\end{array}$
边界情况：$d{p}_{0,0}=0,a_0=0$。这样就把初始状态设为了站在 $0,0$。
答案： min ⁡ d p t o t , i ( i ∈ { 0 , 1 , 2 , 3 , 4 } ) \min dp_{tot,i}(i\in\{0,1,2,3,4\}) mindptot,i​(i∈{0,1,2,3,4})，$tot$ 表示箭头个数。
注意：每组数据要把 $d{p}_{i,j}$ 重新设为 0x3f3f3f3f；$tot$ 设为 $0$，重新开始统计箭头个数。

代码

#include<bits/stdc++.h>
using namespace std;
int tot,a[100005],dp[100005][5];
int cal(int x,int y){
	if(x==0||y==0) return 2;
	if(abs(x-y)==1) return 3;
	if(x==1&&y==4||x==4&&y==1) return 3;
	return 4;
}
int main(){
	while(1){
		tot=0;
		cin>>a[++tot];
		if(a[tot]==0) break;
		while(cin>>a[++tot])
			if(a[tot]==0){
				tot--;
				break;
			}
		memset(dp,0x3f,sizeof(dp));
		dp[0][0]=0;
		for(int i=0;i<tot;i++)
			for(int j=0;j<=4;j++){
				if(a[i+1]==a[i]) dp[i+1][j]=min(dp[i+1][j],dp[i][j]+1);
				else if(a[i+1]==j) dp[i+1][a[i]]=min(dp[i+1][a[i]],dp[i][j]+1);
				else{
					dp[i+1][j]=min(dp[i+1][j],dp[i][j]+cal(a[i],a[i+1]));
					dp[i+1][a[i]]=min(dp[i+1][a[i]],dp[i][j]+cal(j,a[i+1]));
				}
			}
		cout<<min(min(min(dp[tot][1],dp[tot][2]),min(dp[tot][3],dp[tot][4])),dp[tot][0])<<endl;
	}
	return 0;
}