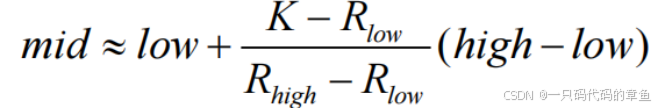查找(检索):
定义:从给定的数据中找到对应的K
1,顺序查找:
O(n)的从前向后的遍历
2,对半查找,要求有序
从中间开始查找,每次检查中间的是否正确,不正确就根据性质去左边or右边找
2.1对半插入排序
在找位置的时候是logn 去找, 但是最后需要换位置 排序之后仍然是O()N^2)
对同一序列分别进行对半插入排序和直接插入排序,两者之间
可能的不同之处是___D___。【考研题全国卷】
A.排序的总趟数
B.元素的移动次数
C.使用辅助空间的数量
D.元素的比较次数
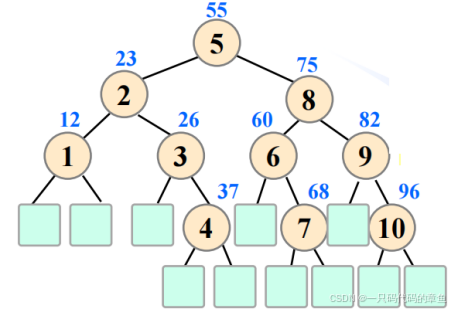
2.2二叉判定树(扩充二叉树):
在二叉树中空指针的位置,都增加特殊的结点(空叶结点),由此生成的二叉树称为扩充二叉树。称圆形结点为内结点,方
形结点为外结点
➢当high-low+1 £ 0时:T(low, high)为空;
➢当high-low+1 > 0时,令mid = ë(low+high)/2û
✓T(low, high)的根结点是mid ;
✓根结点的左子树是Rlow,…,Rmid-1对应的二叉判定树;
✓根结点的右子树是Rmid+1,…,Rhigh对应的二叉判定树。
对半查找算法的每次成功查找正好对应判定树的一个内结点,元素比较次数为该结点的深度加1,即从根到该结点所经过的结点数。
每次不成功的查找对应判定树的一个外结点,元素比较次数恰好为该结点深度,即根到该节点所经过的内结点数
平均失败的查找长度:外节点深度之和/外节点数(3.5)
平均成功查找长度:(内节点深度之和)/内节点数+1 (下面的是2.9)
➢优点:平均查找效率不超过O(logn) ,比顺序查找高。
➢缺点:
✓适用于有序数组,对有序链表难以进行二分查找。
✓适用于静态查找场景,若元素动态变化(频繁增删)后,
为了维持数组有序,需要O(n)时间调整,与顺序查找相比,
就没有优势了。
3,斐波那契查找
斐波那契数列:f0=0,f1=1;fi=fi-1+fi-2
斐波那契查找:
如果一个数组的长度是一个斐波那契数-1 ,那么他的左右就被分为了左边F(k-1)-1,中间一个,右边F(k-1)-;
所以我们可以尝试根据斐波那契数列来优化查找
假定数组中元素个数n是某个斐波那契数减1,即n=Fk-1。
令mid ¬ Fk-1把K与R[mid]比较,若:
➢K < R[mid]:在R[1]…R[Fk-1-1]内继续查找;
➢K > R[mid]:在R[Fk-1+1]…R[Fk-1]内继续查找;
➢K = R[mid]:则查找成功。
int FibSearch(int R[], int n, int K, int F[], int k){
int low=1,high=n;
while(low <= high){
int mid=low+F[k-1]-1; //因为我们的F[k]=f[k-1]+f[k-2],现在以f[k-1]为mid
if(K<R[mid]) {high=mid-1; k--;}//我们抛弃了f[k-2] ,查找范围从low--low+f[k]--->low---low+f[k-1]
//长度为 f[k-1]-1
else if(K>R[mid]) {low=mid+1; k-=2;} //我们抛弃了f[k-1],从low--f[k]--->low+f[k-1]-->low+f[k]
//长度为f[k-2]-1
else return mid;
}
return -1;
}
本质是从黄金比例查找
并且进入左边的几率更大,所需要的比较次数少,
4,插值查找
根据数学所学,根据直线算出可能的横坐标,假设原来的都是均分布且线性增长
平均时间复杂度:loglogn --->n
从O(logn)到O(loglogn)优势并不明显(除非查找表极长,
或比较操作成本极高)。
比如n=232 » 42.9亿
logn = log232 = 32
loglogn= log32 = 5
➢需引入乘除法运算。
➢元素分布不均匀时效率受影响。
➢实际中可行的方法:首先通过插值查找迅速将查找范围缩
小到一定的范围,然后再进行对半查找或顺序查找。
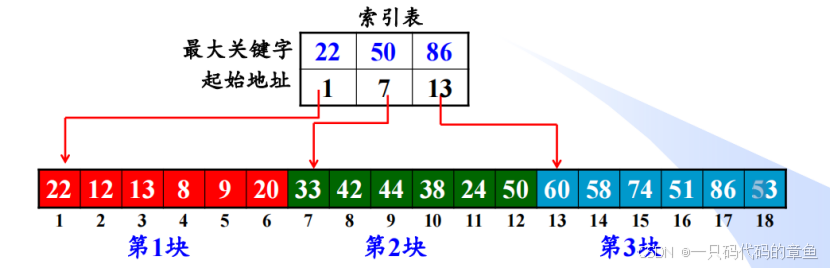
5,分块查找:
将大数组分成若干子数组(块),每个块中的数值都比后一块中数值小(块内不要求有序),建一个索引表记录每个子表的起始地址和各块中的最大关键字
查找的过程:先块间对半查找,再内部顺序查找,类似组相联cache