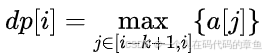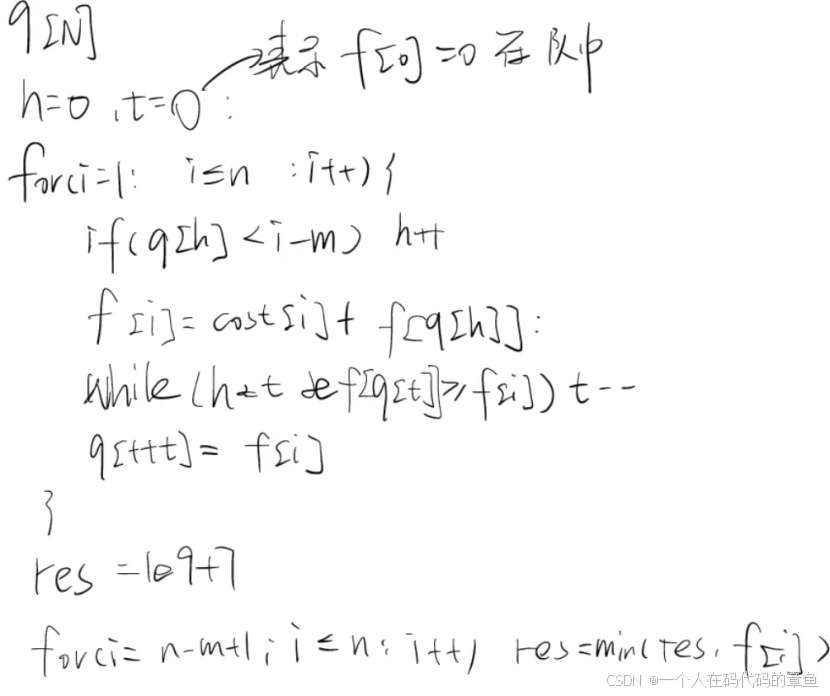单调队列优化dp
单调队列优化动态规划(DP)是一种用于提升动态规划算法效率的技术手段,常用于解决一些在 DP 状态转移过程中存在特定单调性和重叠子问题的场景。
基本概念
动态规划:将一个复杂问题分解为若干子问题,通过求解子问题并保存其结果,避免重复计算,从而解决原问题的算法策略。例如在计算斐波那契数列时,可利用动态规划将其转化为求解一系列子问题 fn = fn-1 + fn-2 ,并保存 fi的值。
单调队列:是一种特殊的队列结构,队列中的元素满足单调性(单调递增或单调递减)。在单调队列中,新元素入队时,会按照特定规则(如保持单调性)将队尾不满足条件的元素出队。比如在一个单调递增队列中,新元素入队时,若队尾元素大于等于新元素,则队尾元素出队,直到队尾元素小于新元素或者队列为空。
适用场景
滑动窗口类 DP 问题:例如给定一个数组和一个固定大小的窗口,每次窗口滑动时需要快速求出窗口内的最值等问题。在动态规划中,当状态转移涉及到在一个滑动窗口内寻找最优值,且窗口随着状态的推进而移动时,可使用单调队列优化。
具有决策单调性的 DP 问题:即状态转移方程中的最优决策点随着状态的变化呈现一定的单调性。比如在某些背包问题或路径规划问题中,若最优决策点的位置随着背包容量或路径长度等状态变量的增加而单调变化,就可能适合用单调队列优化。
优化原理
在动态规划中,状态转移常常需要在一个区间内寻找最优值,而这个区间可能随着状态的推进而变化。如果直接遍历区间来寻找最优值,时间复杂度较高。单调队列通过维护元素的单调性,使得在队首或队尾可以快速获取到区间内的最优值(如最大值或最小值),从而避免了对区间内元素的重复遍历,将时间复杂度从 n^2等较高复杂度降低到接近 n,提升了算法效率。
实现步骤
定义状态:根据问题确定动态规划的状态,例如dpi 表示到第i 个位置时的最优解等。
确定状态转移方程:明确如何从已有的状态推导出新的状态,如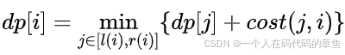
维护单调队列:在计算状态dpi时,根据状态转移方程的特点,将可能的决策点(如j )按照一定规则(如与dpi或 cost (j,i)相关的规则)加入单调队列。在加入新元素时,按照单调性规则调整队列,确保队列的单调性。
获取最优值:根据单调队列的性质,从队首或队尾获取当前状态的最优决策点对应的dp值,用于计算dp i。
更新队列:随着状态的推进,可能需要从队列中移除不再属于当前决策区间的元素,以保持队列的有效性。
示例(引例)
问题:给定一个数组a和一个大小为k 的滑动窗口,从数组的第一个元素开始,窗口每次向右滑动一个位置,求每次滑动后窗口内的最大值。
状态定义:dp i 表示以a[i]为窗口右边界时窗口内的最大值。
状态转移方程:
单调队列维护:维护一个单调递减队列,队列中存储数组元素的下标。每次处理a[i] 时,将队尾元素对应的a[x]值小于a[i]的下标出队,然后将i加入队列。同时,若队首元素的下标小于 i-k+1(即不在当前窗口内),将队首元素出队。
获取最优值:队首元素对应的a值即为dp[i] 。
通过这种方式,利用单调队列优化了在每个窗口内寻找最大值的过程,提高了算法效率。
(对单调队列的自己的见解:单调队列可以用爬山形象的来比喻:我们的视野范围就是窗口的大小,当我们翻过一个山头之后,我们就看不见山头那边的景色了,反应在数组中就是 (1,3,-1,),当我们遍历到-1的时候,假设我们的窗口是3,但是我们只能看见3,看不见3前面的1但是3后面的-1还是看的见的,因为这个-1可能成为新的山头,(1,3,-1,-2,-3))
习题1(最大子序和):
分析:
这是一道经典的序列优化问题,核心在于在给定整数序列中找出满足长度限制的最大连续子序列和
输入:给定一个长度为n 的整数序列 a0,a1...an-1 ,以及一个正整数 m,表示连续子序列的长度上限。
任务:从该整数序列中找出一段长度不超过m的连续子序列,使得这个子序列中所有数的和最大。
前缀和 + 单调队列法
思路:
首先计算前缀和数组s,这样,以j为结束位置,长度len的连续子序列的和就可以表示为s[j]-s[j-len]。
维护一个单调队列,队列中存储前缀和数组的下标。对于每个位置i,计算s[i] ,然后根据队列性质进行操作:
-1:当队列不为空且i-q.front()>m(q为单调队列)时,队首元素出队,以保证队列中存储的是长度不超过m 的子序列对应的前缀和下标。
-2:当队列不为空且s[i]<=s[]q.back()时,队尾元素出队,保持队列单调递减(这样队首元素对应的前缀和是当前窗口内最小的,用于计算最大子序列和)。入果之后有一个值的前缀和是m。m-s[i]==m-s[q.back],但是明显第一个的长度更短,不会用到第二个,所以可以将队尾弹出
-3:i入队
-4:用s[i]-s[q.front()]更新最大子序列和
举例:
伪代码:
习题2(旅行问题)
分析:
背景设定:John 打算驾驶汽车周游环形公路,公路上有 个车站,各车站存有一定油量(可能为零),每升油可让汽车行驶一千米。
行驶规则:John 需从某一车站出发,沿顺时针或逆时针方向遍历所有车站并回到起点,出发时汽车油量为零,到达每个车站时将该站油量全部带上,行驶中不能出现没油的情况。
任务目标:判断以每个车站 为起点能否按照上述条件成功周游一周。
解题思路
这里的队列维护的是一个最难以成功的一系列成员,列出我们能够转移的条件,发现只有在从i到i的一个循环中的任意一个前缀和都大于0,才能够成功,s[j]-s[i-1]>0,那么我们就维护一个最小的s[j],看他能不能满足条件即可
伪代码:
习题3(烽火传递):
分析:
背景设定:烽火台作为重要军事防御设施,建在交通要道或险要处,用于传递军情(白天浓烟,晚上火光)。在某两个城市之间有n座烽火台,每座烽火台发出信号有一定代价。
信号传递规则:为保证情报准确传递,要求在连续m个烽火台中至少有一个发出信号。
任务目标:给定 n、m 以及每个烽火台发信号的代价,计算在这两个城市之间准确传递情报所需花费的总代价最小值。
伪代码:
习题4(绿色通道):
分析:
这是一道结合时间限制与题目选择的优化问题,关键在于在规定时间内选择题目抄写,以最小化最长空题段的长度
任务背景:高二数学《绿色通道》有n道题目需抄写,编号为 1,2,3,4.....抄写第i题需花费ai分钟。小 Y 仅有不超过t分钟的抄写时间,必然会有题目空着。
空题段定义:下标连续的一些空题构成一个空题段,其长度为所包含的题目数量。
目标设定:最长空题段长度会引发马老师的愤怒,小 Y 想知道在t分钟内选择抄写哪些题,能使最长空题段的长度尽可能小,只需输出这个最小的最长空题段长度。
思路:
因为要找出最大的满足空题段的大小,所以我们可以用二分来做,取mid为(l+r)/2,检查mid空题段下能不能满足条件,1,如果能,说明t分钟能做更多的题,让老师的愤怒值更低,那么我们就去查找l,mid区间里找到更小的空题段,让老师的怒气值更小 。2,如果不能,就让l=mid,去mid,r 里面去找符合条件的空题段大小
如何检查mid是否合法尼?这不就是上一个题吗?这里最多空出m个题目,就是上一个题目的‘不允许空出连续的m+1个烽火台’
伪代码:
习题5(修建草坪):
分析:
这是一道关于资源(奶牛)分配以实现效益(效率)最大化的问题,关键在于在满足奶牛连续工作数量限制的条件下,找出能获得最大效率的安排方案,以下从问题描述、解题思路等方面进行分析:
背景设定:FJ 在赢得小镇最佳草坪比赛一年后变得懒惰,未修剪草坪。新一轮比赛开始,FJ 希望再次夺冠,但草坪脏乱,只能让奶牛完成工作。
奶牛相关信息:FJ 有N只排成一排的奶牛,编号为1 到N ,每只奶牛效率不同,奶牛i的效率为Ei 。
限制条件:编号相邻的奶牛很熟悉,若 FJ 安排超过K只编号连续的奶牛工作,这些奶牛就会罢工去开派对。
任务目标:找到最合理的安排方案,计算 FJ 能得到的最大效率。
这个题和抢家劫舍很像,这里是不能连续的抢劫联系的k个屋子