2021-12-23【数据结构课程设计】【关键路径】，2024年最新2024最后一次Java面试

SElemType *top;

int stacksize;

}SqStack;

Status InitStack(SqStack &S){

S.base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));

if (!S.base)

exit(_OVERFLOW);

S.top = S.base;

S.stacksize = STACK_INIT_SIZE;

return OK;

}

Status StackEmpty(SqStack S){

if (S.top == S.base)

return TRUE;

else

return FALSE;

}

Status GetTop(SqStack s,SElemType &e){

if(s.base==s.top)

return 0;

e = *(s.top - 1);

return 1;

}

Status Push(SqStack &S, SElemType e){

if (S.top - S.base >= S.stacksize) {

S.base = (SElemType *)realloc(S.base, (S.stacksize + STACKINCREMENT) * sizeof(SElemType));

if (!S.base)

exit(_OVERFLOW);

S.top = S.base + S.stacksize;

S.stacksize += STACKINCREMENT;

}

*(S.top)++ = e;

return OK;

}

Status Pop(SqStack &S, SElemType &e){ /* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */

if (S.top == S.base)

return ERROR;

e = *–S.top;

return OK;

}

int ve[MAX_VERTEX_NUM], vl[MAX_VERTEX_NUM];//e[]：最早发生时间 vl[]:最迟发生时间

bool flag = 0;

vector path;

int top,down;

void dfs(ALGraph G, int u){

if (G.vertices[u].data == G.vertices[top].data) {//搜索到终点

if (flag) cout << “\n或者：\n”;

cout << G.vertices[down].data; //输出起点

for(auto &it:path) //遍历输出关键路径

cout << it;

flag = 1;

return;

}

ArcNode* p = G.vertices[u].firstarc; //初边

for (; p; p = p->nextarc) { //遍历

int k = p->adjvex; //该弧所指向的顶点的下标

int dut = *(p->info); //弧的权值

if (ve[u] == vl[k] - dut) { //是关键活动

path.push_back(“->”);

path.push_back(G.vertices[k].data); //记录关键活动

dfs(G, k); //继续DFS搜索下一个结点的关键活动

path.pop_back(); //回溯

}

//算法7.13

Status TopologicalOrder(ALGraph G, SqStack &T){

int j, k, count, indegree[MAX_VERTEX_NUM],e;

SqStack S;

ArcNode *p;

FindInDegree(G, indegree);

InitStack(S);

for (j = 0; j < G.vexnum; ++j)

if (!indegree[j])

Push(S, j);

GetTop(S, down); //记录起点位置

InitStack(T);

count = 0;

for (j = 0; j < G.vexnum; ++j)

ve[j] = 0; //初始化

while (!StackEmpty(S)){

Pop(S, j);

Push(T, j);

++count; //入栈的顶点数

for (p = G.vertices[j].firstarc; p; p = p->nextarc){ //遍历邻接表

k = p->adjvex; //该弧所指向的顶点的下标

if (–indegree[k] == 0) //入度减为零入栈

Push(S, k);

if (ve[j] + *(p->info) > ve[k])//拓扑正序更新max

ve[k] = ve[j] + *(p->info);

}

if (count < G.vexnum){

printf(“此有向网有回路\n”);

return ERROR;

}

else{

GetTop(T, top);//拓扑排序的最后一个结点为终点

return OK;

}

//算法7.14

Status CriticalPath(ALGraph G){

SqStack T;

int i, j, k, ee, el;

ArcNode *p;

char dut, tag;

if (!TopologicalOrder(G, T)) // 产生有向环

return ERROR;

j = ve[0];

for (i = 1; i < G.vexnum; i++) //j=Max(ve[]) 完成点的值

if (ve[i] > j)

j = ve[i];

int maxn = j;

for (i = 0; i < G.vexnum; i++) // 初始化顶点事件的最迟发生时间(最大值)

vl[i] = j; // 完成点的最早发生时间

while (!StackEmpty(T)) // 按拓扑逆序求各顶点的vl值

for (Pop(T, j), p = G.vertices[j].firstarc; p; p = p->nextarc){

k = p->adjvex;

dut = *(p->info); // dut<j,k>

if (vl[k] - dut < vl[j])

vl[j] = vl[k] - dut;

}

printf(" j k dut ee el tag\n");

for (j = 0; j < G.vexnum; ++j)//求ee,el和关键活动

for (p = G.vertices[j].firstarc; p; p = p->nextarc){

k = p->adjvex;

dut = *(p->info);//边权

ee = ve[j];

el = vl[k] - dut;

tag = (ee == el) ? ‘*’ : ’ ';

printf(“%2d %2d %3d %3d %3d %c\n”, j, k, dut, ee, el, tag);

}

printf(“关键活动为:\n”);

for (j = 0; j < G.vexnum; ++j)

for (p = G.vertices[j].firstarc; p; p = p->nextarc){

k = p->adjvex;

dut = *(p->info);

if (ve[j] == vl[k] - dut)

printf(“%s→%s\n”, G.vertices[j].data, G.vertic

必看视频！获取2024年最新Java开发全套学习资料

es[k].data); // 输出关键活动

}

printf(“关键路径为：\n”);

dfs(G,0);

printf(“\n花费时间最少为：%d\n”, maxn);

return OK;

}

int main(){

ALGraph h;

CreateGraph(h);

Display(h);

CriticalPath(h);

}

测试样例：

在这里插入图片描述

再加两条：

v1 -> v10(权值为8)

v10 -> v9(权值为10)

测试数据：

请输入图的顶点数和边数(空格隔开): 10 13

请输入10个顶点的值(<5个字符):

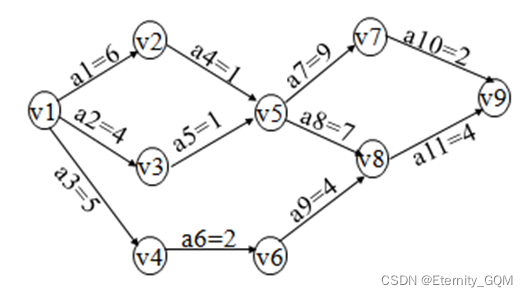
v1 v2 v3 v4 v5 v6 v7 v8 v9 v10

请顺序输入每条弧(边)的权值、弧尾和弧头(以空格作为间隔):

6 v1 v2

4 v1 v3

5 v1 v4

1 v2 v5

1 v3 v5

2 v4 v6

9 v5 v7

7 v5 v8

4 v6 v8

2 v7 v9

4 v8 v9

8 v1 v10

10 v10 v9

运行结果

有向图

10个顶点：

v1 v2 v3 v4 v5 v6 v7 v8 v9 v10

13条弧(边):

v1→v10 :8v1→v4 :5v1→v3 :4v1→v2 :6

v2→v5 :1

v3→v5 :1

v4→v6 :2

v5→v8 :7v5→v7 :9

v6→v8 :4

v7→v9 :2

v8→v9 :4

v10→v9 :10

j k dut ee el tag

0 9 8 0 0 *

0 3 5 0 3

0 2 4 0 2

0 1 6 0 0 *

1 4 1 6 6 *

2 4 1 4 6

3 5 2 5 8

4 7 7 7 7 *

4 6 9 7 7 *

5 7 4 7 10

6 8 2 16 16 *

7 8 4 14 14 *

9 8 10 8 8 *

关键活动为:

v1→v10

v1→v2

v2→v5

v5→v8

v5→v7

v7→v9

v8→v9

v10→v9

关键路径为：

v1->v10->v9

或者：

v1->v2->v5->v8->v9

或者：

v1->v2->v5->v7->v9

花费时间最少为：18

心得体会

在使用邻接表存图过程中再次熟悉链表相关操作。
复习栈的编写及使用。利用栈求解拓扑序列。
在进行拓扑排序时，掌握结点度（入度）求取，学会拓扑有序的应用：利用拓扑排序进行最早发生时间的计算。
复习栈的编写及使用。利用栈存储拓扑有序序列，出栈即得到拓扑逆序序列。并利用拓扑逆序求解最晚发生时间的计算。
复习图上深度优先搜索。利用DFS输出关键路径。

参考文献

[1] 严蔚敏，吴伟民.数据结构（C语言版）[M]. 北京：清华大学出版社，1997.4

2021-12-30 更新

================================================================================

1. dfs()起点位置不正确：

错误代码：

dfs(G,0);

正确代码：

dfs(G,down);

0并不是起点的下标，down才是。

例如测试样例改为：

请输入图的顶点数和边数(空格隔开): 9 11

请输入9个顶点的值(<5个字符):

v2 v1 v3 v4 v5 v6 v7 v8 v9

请顺序输入每条弧(边)的权值、弧尾和弧头(以空格作为间隔):

6 v1 v2

4 v1 v3

5 v1 v4

1 v2 v5

1 v3 v5

2 v4 v6

9 v5 v7

7 v5 v8

4 v6 v8

2 v7 v9

4 v8 v9

dfs(G,0)会输出：

有向图

9个顶点：

v2 v1 v3 v4 v5 v6 v7 v8 v9

11条弧(边):

v2→v5 :1

v1→v4 :5v1→v3 :4v1→v2 :6

v3→v5 :1

v4→v6 :2

v5→v8 :7v5→v7 :9

v6→v8 :4

v7→v9 :2

v8→v9 :4

j k dut ee el tag

0 4 1 6 6 *

1 3 5 0 3

1 2 4 0 2

1 0 6 0 0 *

2 4 1 4 6

3 5 2 5 8

4 7 7 7 7 *

4 6 9 7 7 *

5 7 4 7 10

6 8 2 16 16 *

7 8 4 14 14 *

关键活动为:

v2→v5

v1→v2

v5→v8

v5→v7

v7→v9

v8→v9

关键路径为：

v1->v5->v8->v9 //错误

或者：

v1->v5->v7->v9

花费时间最少为：18

dfs(G,down)会输出：

有向图

9个顶点：

v2 v1 v3 v4 v5 v6 v7 v8 v9

11条弧(边):

v2→v5 :1

v1→v4 :5v1→v3 :4v1→v2 :6

v3→v5 :1

v4→v6 :2

v5→v8 :7v5→v7 :9

v6→v8 :4

v7→v9 :2

v8→v9 :4

j k dut ee el tag

0 4 1 6 6 *

1 3 5 0 3

1 2 4 0 2

1 0 6 0 0 *

2 4 1 4 6

3 5 2 5 8

4 7 7 7 7 *

4 6 9 7 7 *

5 7 4 7 10

6 8 2 16 16 *

7 8 4 14 14 *

关键活动为:

v2→v5

v1→v2

v5→v8

v5→v7

v7→v9

v8→v9

关键路径为：

v1->v2->v5->v8->v9 //正确

或者：

v1->v2->v5->v7->v9

花费时间最少为：18

2. dfs()另一种记录方式：

char* strcmmp(char *a,int n){

char arr=(char)malloc(n*sizeof(char));

for(int i=0;i<n-1;i++){

arr[i]=a[i];

}

arr[n-1]=‘\0’;

return arr;

}

void dfs(ALGraph G,int u,char arry[])

{

if(G.adjlist[u].vex==G.adjlist[top].vex)

{

//printf(“%s”,G.adjlist[down].vex);

for(int i=0;i<strlen(arry);i++)

{

printf(“%c”,arry[i]);

if(i>=0&&i<strlen(arry)-1)

printf(“->”);

}

printf(“\n”);

return ;

}

EdgeNode *p=G.adjlist[u].firstedge;

for(;p;p=p->next)

{

int k=p->adjvex,w=p->weight;

if(etv[u]==ltv[k]-w)

{ //printf(“%d\n”,k);

arry=strcat(arry,G.adjlist[k].vex);

dfs(G,k,arry);

arry=strcmmp(arry,strlen(arry)-1);

}

3. C语言完整代码：

#include <stdio.h>

#include <stdlib.h>

#include <string.h>

#define Max_VERTEX_NUM 20

#define ElemType int

#define Status int

#define MAXVEX 100

#define MAX_NAME 5

int top, down;

int *etv, *ltv; //记录事件最早发生时间和最迟发生时间数组

typedef char VertexType[MAX_NAME];

typedef struct nodee //边表节点

{

int adjvex; //邻接点域,存储该顶点对应的下标

int weight; //权值

struct nodee *next; //指向下一个顶点

} EdgeNode;

typedef struct vnode //顶点

{

VertexType vex; //顶点信息

EdgeNode *firstedge; //指向顶点的第一个邻接顶点

} VertexNode, AdjList[Max_VERTEX_NUM];

typedef struct AlGraph

{

AdjList adjlist;

int vexnum; //节点数目

int edgenum; //边的数目

} ALGraph;

//定义一个栈

typedef struct Node

{

ElemType data; //存储数据

struct Node *next; //指向下一个元素

} node, *LinkStackptr;

typedef struct LS

{

LinkStackptr top;

int count; //记录栈中元素的个数

} LinkStack;

Status InitStack(LinkStack *s) //创建一个栈

{

s->top = (LinkStackptr)malloc(sizeof(node));

if (s->top == NULL)

exit(0);

s->top->next = NULL;

s->count = 0;

return 1; //建栈成功返回1

}

Status StackEmpty(LinkStack s) //判断是否为空

{

if (s.count == 0)

return 1; //若栈为空返回1

return 0; //若栈不为空返回 0

}

Status GetTop(LinkStack s, int *e) //返回栈顶元素

{

if (s.top == NULL)

return 0;

*e = s.top->data;

return *e;

}

Status Push(LinkStack *s, ElemType e) //元素入栈(头插）

{

LinkStackptr p = (LinkStackptr)malloc(sizeof(node));

if (p == NULL)

return 0;

p->data = e;

p->next = s->top;

s->top = p; //指向第一个元素的指针

s->count++; //栈中元素个数增加

return 1;

}

Status pop(LinkStack *s, ElemType *e) //返回栈顶元素 ,并删除 (头删)

{

if (s->top == NULL)

return 0;

LinkStackptr p = s->top->next; //指向下一个元素

*e = s->top->data; //将首元素的赋给e

free(s->top);

s->top = p; //删除节点

s->count = s->count - 1; //栈中元素个数减少

return *e; //返回e

}

void CreateALG(ALGraph *ALG, int **indegree) //创建一个图(邻接表存储)

{

printf("请输入节点的数目和边的数目 ");

scanf(“%d%d”, &ALG->vexnum, &ALG->edgenum);

int i, j, k, w;

EdgeNode *e;

for (i = 0; i < ALG->vexnum; i++)

{

getchar();

// printf(“请输入第%d个节点的信息”,i+1);

scanf(“%s”, ALG->adjlist[i].vex); //输入结点信息

ALG->adjlist[i].firstedge = NULL;

}

for (k = 0; k < ALG->edgenum; k++) //边表的建立

{

getchar();

//printf(“请输入第%d条边<vi,vj>上的顶点序号和权值”,k+1);

scanf(“%d%d%d”, &w, &i, &j);

e = (EdgeNode *)malloc(sizeof(EdgeNode));

e->adjvex = j - 1;

e->weight = w;

e->next = ALG->adjlist[i - 1].firstedge;

ALG->adjlist[i - 1].firstedge = e; //将结点插入

}

*indegree = (int *)malloc(ALG->vexnum * sizeof(int)); //创建indegree数组求入度

for (i = 0; i < ALG->vexnum; i++)

{

(*indegree)[i] = 0; //(indegree初始化)

}

void FindInDegree(ALGraph ALG, int indegree[]) //求各个结点的入度

{

int i;

EdgeNode *temp;

for (i = 0; i < ALG.vexnum; i++) //对每个顶点的边表都进行遍历

{

temp = ALG.adjlist[i].firstedge;

while (temp != NULL)

{

indegree[temp->adjvex]++;

temp = temp->next;

}

char *strcmmp(char *a, int n)

{

char *arr = (char *)malloc(n * sizeof(char));

for (int i = 0; i < n - 1; i++)

{

arr[i] = a[i];

}

arr[n - 1] = ‘\0’;

return arr;

}

void dfs(ALGraph G, int u, char arry[])

{

if (G.adjlist[u].vex == G.adjlist[top].vex)

{

//printf(“%s”,G.adjlist[down].vex);

for (int i = 0; i < strlen(arry); i++)

{

printf(“%c”, arry[i]);

if (i >= 0 && i < strlen(arry) - 1)

printf(“->”);

}

printf(“\n”);

return;

}

EdgeNode *p = G.adjlist[u].firstedge;

for (; p; p = p->next)

{

int k = p->adjvex, w = p->weight;

if (etv[u] == ltv[k] - w)

{ //printf(“%d\n”,k);

arry = strcat(arry, G.adjlist[k].vex);

dfs(G, k, arry);

arry = strcmmp(arry, strlen(arry) - 1);

}

Status TopologicalSort(ALGraph ALG, int indegree[], LinkStack *T) //拓扑排序

{

int i, count = 0, k;

LinkStack s;

EdgeNode *p;

总结

互联网大厂比较喜欢的人才特点：对技术有热情，强硬的技术基础实力；主动，善于团队协作，善于总结思考。无论是哪家公司，都很重视高并发高可用技术，重视基础，所以千万别小看任何知识。面试是一个双向选择的过程，不要抱着畏惧的心态去面试，不利于自己的发挥。同时看中的应该不止薪资，还要看你是不是真的喜欢这家公司，是不是能真的得到锻炼。其实我写了这么多，只是我自己的总结，并不一定适用于所有人，相信经过一些面试，大家都会有这些感触。

**另外本人还整理收藏了2021年多家公司面试知识点以及各种技术点整理 **

下面有部分截图希望能对大家有所帮助。

在这里插入图片描述
r *a, int n)

{

char *arr = (char *)malloc(n * sizeof(char));

for (int i = 0; i < n - 1; i++)

{

arr[i] = a[i];

}

arr[n - 1] = ‘\0’;

return arr;

}

void dfs(ALGraph G, int u, char arry[])

{

if (G.adjlist[u].vex == G.adjlist[top].vex)

{

//printf(“%s”,G.adjlist[down].vex);

for (int i = 0; i < strlen(arry); i++)

{

printf(“%c”, arry[i]);

if (i >= 0 && i < strlen(arry) - 1)

printf(“->”);

}

printf(“\n”);

return;

}

EdgeNode *p = G.adjlist[u].firstedge;

for (; p; p = p->next)

{

int k = p->adjvex, w = p->weight;

if (etv[u] == ltv[k] - w)

{ //printf(“%d\n”,k);

arry = strcat(arry, G.adjlist[k].vex);

dfs(G, k, arry);

arry = strcmmp(arry, strlen(arry) - 1);

}

Status TopologicalSort(ALGraph ALG, int indegree[], LinkStack *T) //拓扑排序

{

int i, count = 0, k;

LinkStack s;

EdgeNode *p;

总结

**另外本人还整理收藏了2021年多家公司面试知识点以及各种技术点整理 **

下面有部分截图希望能对大家有所帮助。

[外链图片转存中…(img-9n0918Po-1720153912692)]