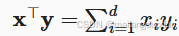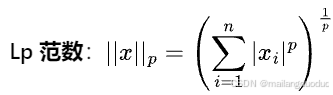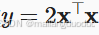前言

本篇博客主要介绍了在学习pytorch前需要了解的一些基本操作，包括张量的概念，基本运算，自动求导等方面。

1.数据操作

1.1数组

N维数组是机器学习和神经网络的主要数据结构，可分为一维数组（向量）、二维数组（矩阵）、多维数组三个类别,在pytorch又常称为张量
标量：由只有一个元素的张量表示
向量：可以被视为标量值组成的列表
矩阵：将向量从一阶推广到二阶

1.1.1创建数组

需要确定形状、数据类型、元素值

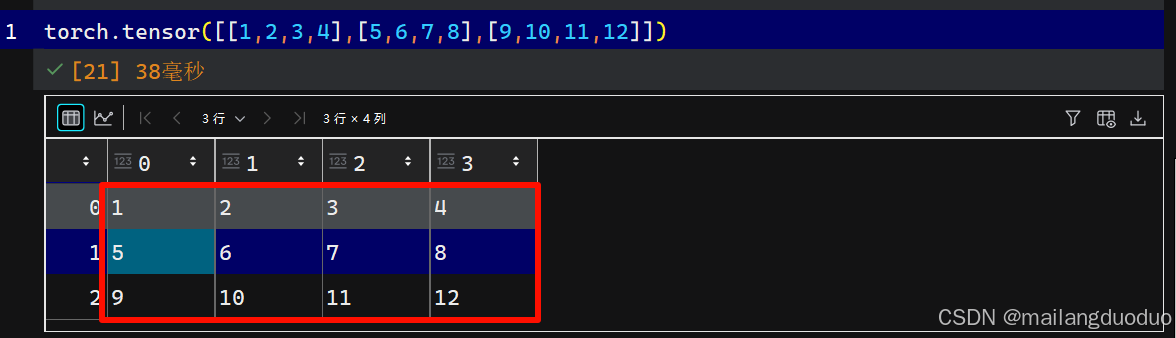
import torch
torch.tensor([[1,2,3,4],[5,6,7,8],[9,10,11,12]])

1.1.2元素的访问

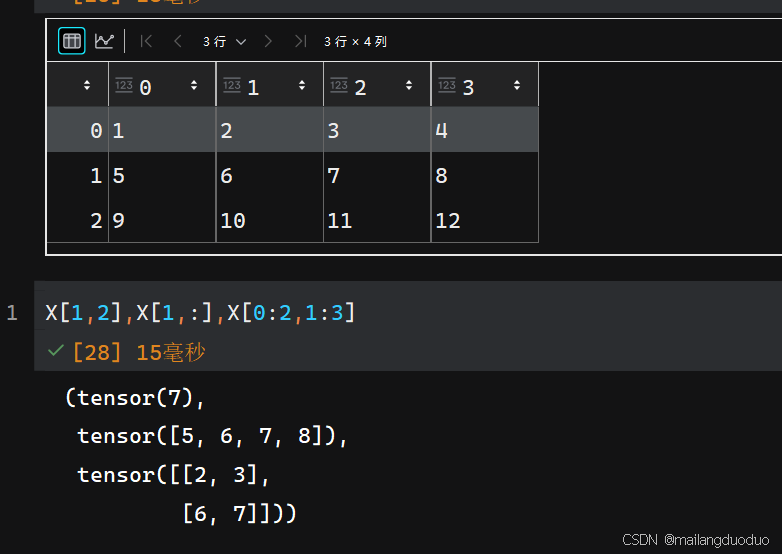
• 单个元素的访问：元素下标从0开始，确定待访问元素的下标即可

• 某一行或某一列：确定行标或者列标，另一个设为：即可，此处以二维数组为例

• 特定元素：按照切片操作即可（起始坐标：结束坐标：步长）
  

1.2算术运算

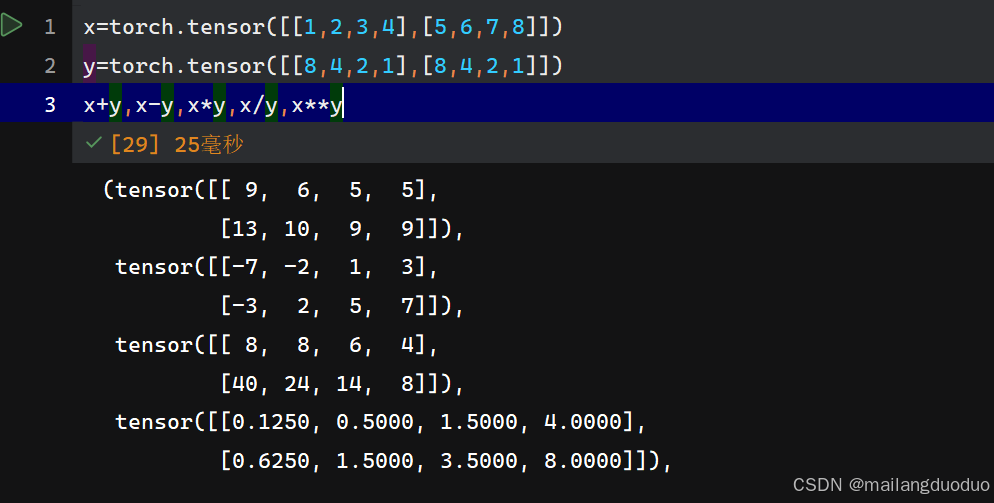
按照元素逐元素进行运算（+、-、*、/、**），并不改变张量的形状

x=torch.tensor([[1,2,3,4],[5,6,7,8]])
y=torch.tensor([[8,4,2,1],[8,4,2,1]])
x+y,x-y,x*y,x/y,x**y

1.3张量的连接

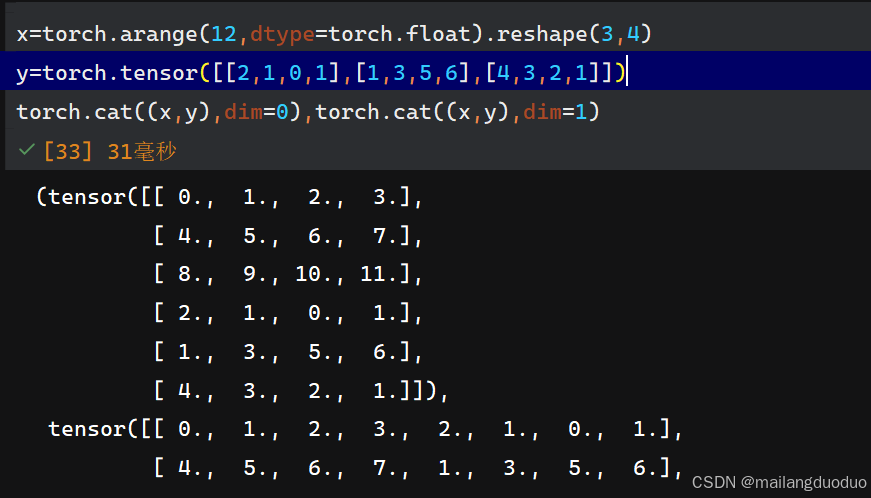
使用cat()函数进行连接：dim=0:按行合并，dim=1:按列合并

x=torch.arange(12,dtype=torch.float).reshape(3,4)
y=torch.tensor([[2,1,0,1],[1,3,5,6],[4,3,2,1]])
torch.cat((x,y),dim=0),torch.cat((x,y),dim=1)

注：每个元素后面带有.表示该元素数据类型为浮点数

1.4广播机制

通过复制将算数运算中维数不同的张量进行匹配

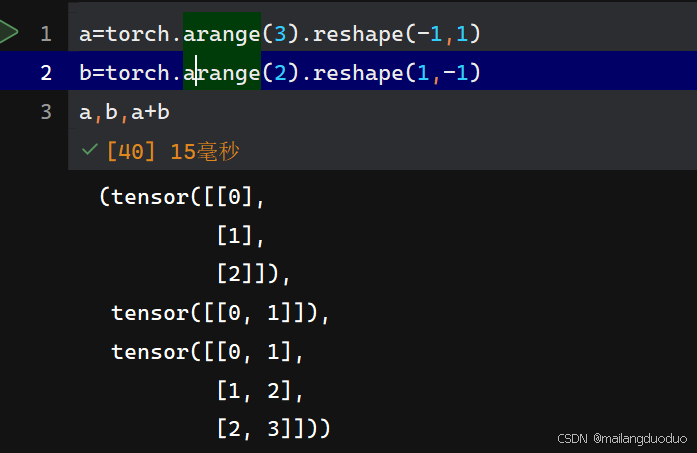
a=torch.arange(3).reshape(-1,1)
b=torch.arange(2).reshape(1,-1)
a,b,a+b

1.5其他基础运算

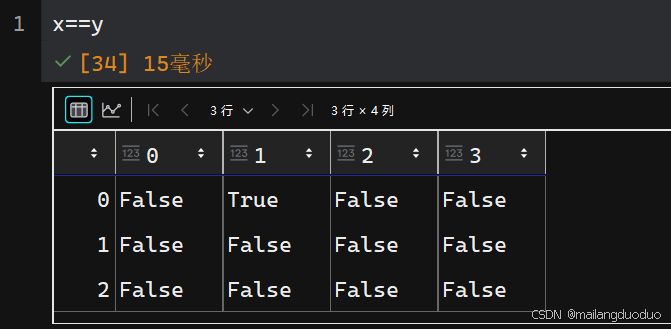
1. 逻辑运算

2 常用函数

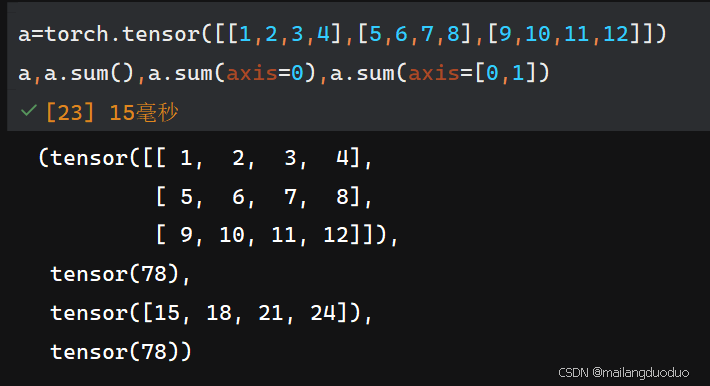
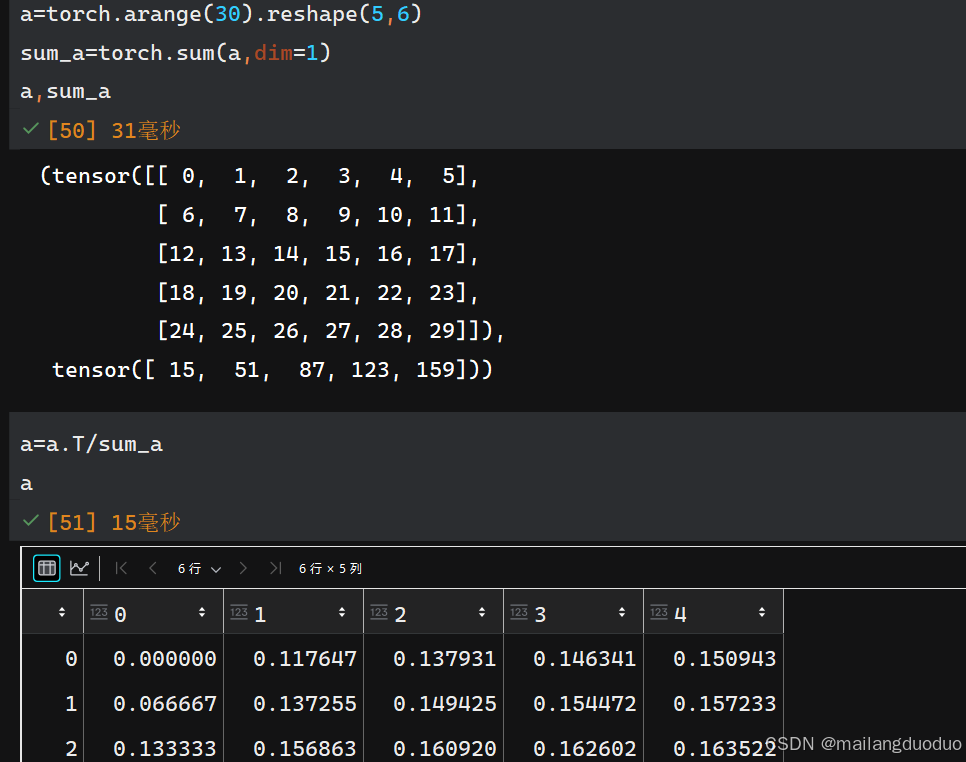
• sum()函数是一种常用的降维手段，默认降维至标量,可以通过axis参数进行指定方向降维

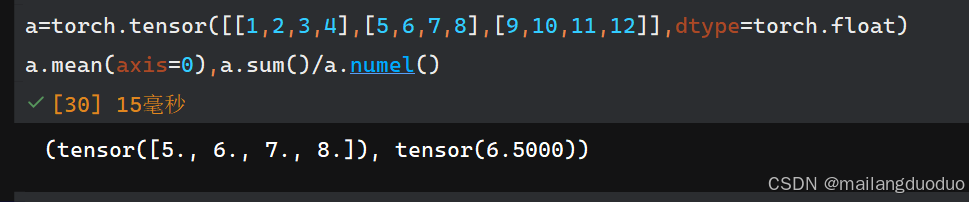
• mean()函数
  同理也是一种降维手段。 注意：修改张量的数据类型，整型无法使用mean（）函数,同理也可以指定方向通过axis参数

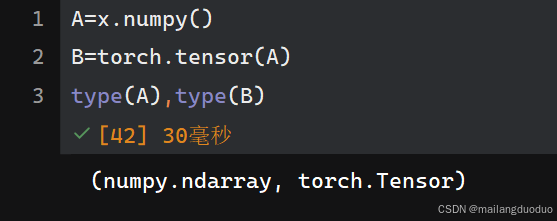
• numpy和tensor转换
  

1.6非降维求和

• 计算每一行或列元素所占的比例，在除法过程中使用了广播机制
  

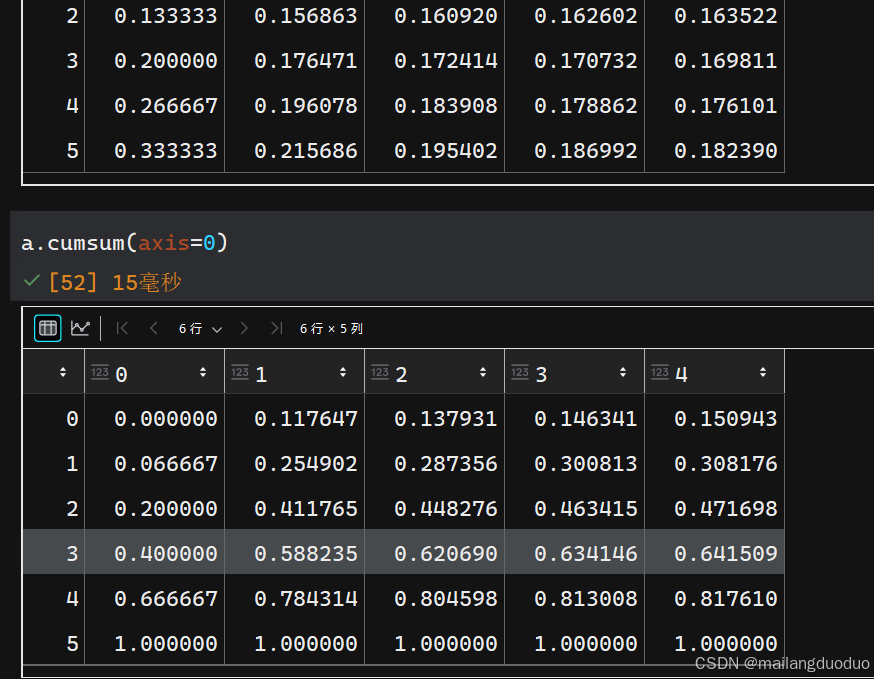
• 计算每一行或列的累计和
  

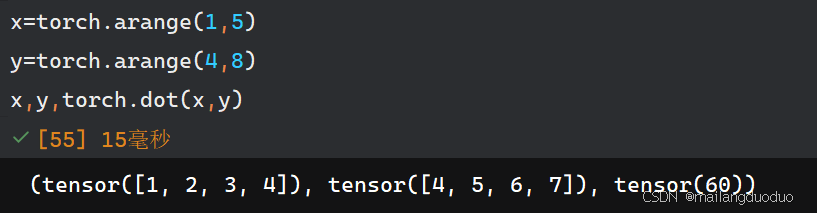
1.7 点积

点积：相同位置元素相乘的累计和


在实际操作中，可以通过此方式实现加权平均的效果

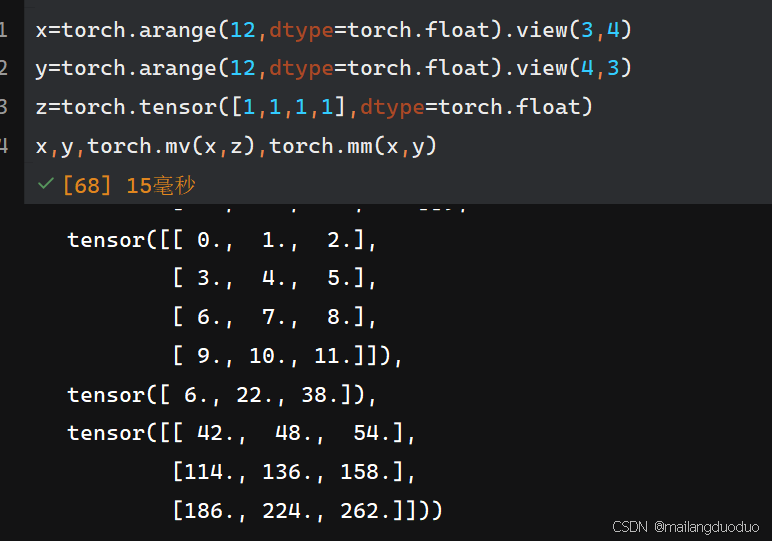
1.8矩阵乘法

mv():用于矩阵与向量的乘法
mm():用于矩阵和矩阵的乘法

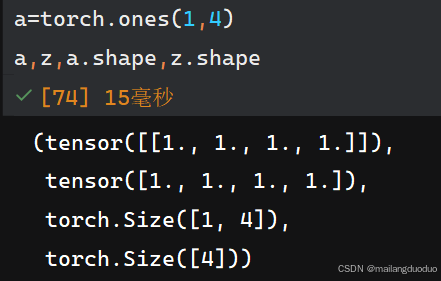
注意区分向量和矩阵，下述例子中，a表示矩阵，z表示向量

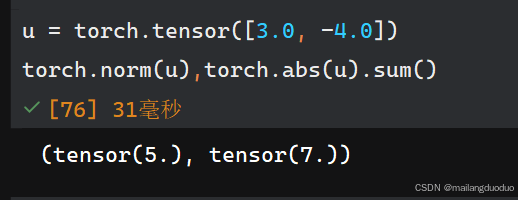
1.9范数

范数：常用于衡量向量或矩阵的大小或长度，分为L1范数、L2范数、P范数
x为n维的向量

2.求导

自动求导：计算一个函数在指定值上的导数

2.1初始化变量及函数

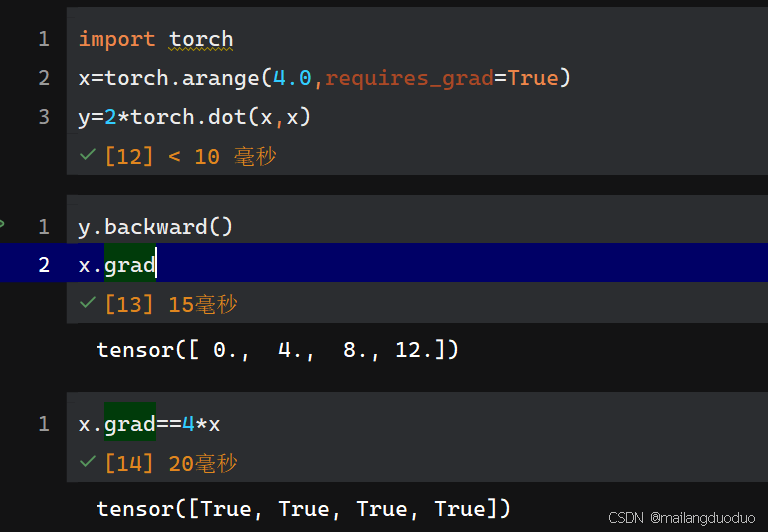
import torch
x=torch.arange(4.0,requires_grad=True)
y=2*torch.dot(x,x)

2.2反向传播求梯度

y.backward()
x.grad

2.3梯度清零

pytorch中梯度会进行累加，所以在进行下一次反向传播前，需要将梯度清零

#%%
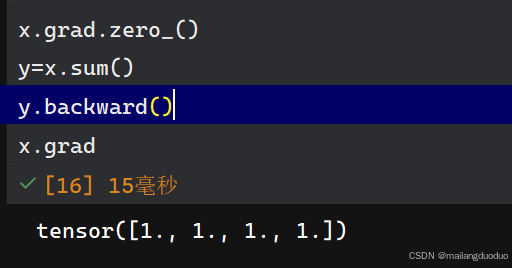
x.grad.zero_()
y=x.sum()
y.backward()
x.grad
#%%

2.4特殊情况

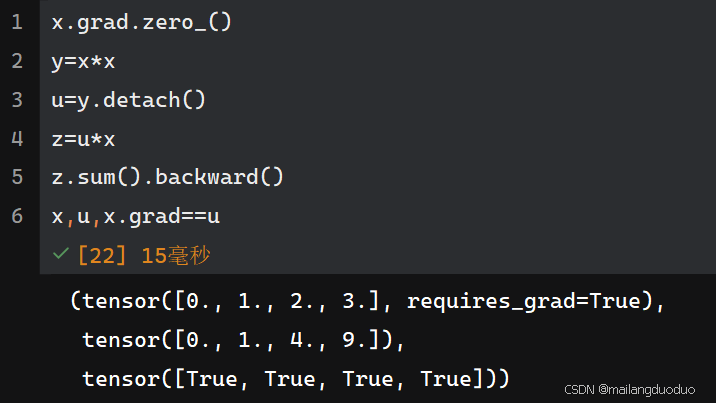
有时需要将某个数视为常数，不参与方向传播的过程，即不作为链式法则的中间变量，此时可以通过detach()函数实现

此时，y是x的函数，u只是一个常数，并不是x的函数，因此可以求y关于x的导数

结语

以上便是pytorch中的基本内容，以及常用的函数，希望能够对你有所帮助，使用的是jupyter notebook