数据结构-时间复杂度-详解
1.前言
1.1数据结构与算法
在计算机科学中,数据结构是一种数据组织、管理和存储的格式。
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。
通俗来讲,数据结构就是如何在内存中对数据进行管理。
而算法就是指如何对内存中的数据进行处理。
1.2如何衡量一个算法的好坏
当小A写了一个快速排序,小B写了一个冒泡排序,二者想要比谁的算法更好。
同样的数据,小A在其低配版的电脑上处理,小B则在高配版的电脑上处理,最后小B的冒泡排序竟比小A的快速排序还快,这能说明快速排序比冒泡排序差吗?显然不能。
为了排除环境差异对算法运行结果的影响,引入了复杂度的概念。
1.3复杂度
复杂度是衡量算法效率的重要标准,分为时间复杂度与空间复杂度,今天讲时间复杂度。
2.时间复杂度
2.1是什么
算法的时间复杂度是一个函数,描述了算法运行时间与输入数据规模之间的关系。
简单讲,时间复杂度就是一个算法运行时,大概的基本操作的执行次数
示例1.1:
int fun(int N)
{
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
//语句一
}
}
for(int i=0;i<2*N;i++)
{
//语句二
}
for(int i=0;i<10;i++)
{
//语句三
}
}
其中语句一被执行N^2次
语句二被执行2*N次
语句三被执行10次
fun()基本操作的执行次数:
| N | 10 | 100 | 1000 |
|---|---|---|---|
| 次数 | 130 | 10210 | 1002010 |
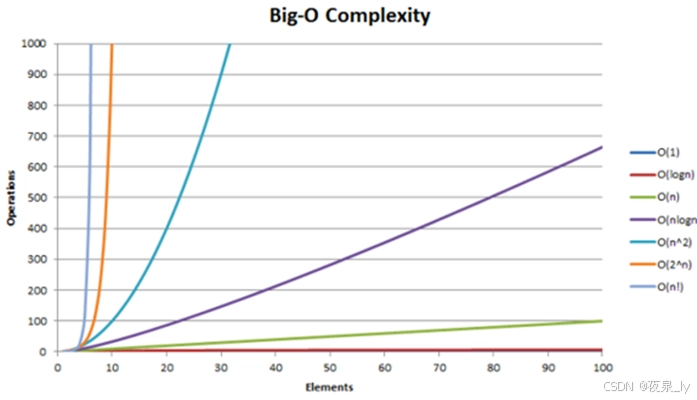
可以看到,随N增大,次数与最高阶的关系最大,因此在分析时间复杂度时,我们通常关注的是算法运行时间随着输入规模趋于无穷大时的趋势,这里我们使用大O符号
2.2大O符号
大O符号(
Big O notation)是用于描述函数渐近行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。
推导方法:
只保留最高阶项
如在上面的示例1.1中,f(N)=N^2 + 2*N + 10 ,只保留最高阶项,则时间复杂度为O(N^2)
不带系数
示例1.2:
int fun(int N)
{
for(int i=0;i<2*N;i++)
{
//语句二
}
for(int i=0;i<10;i++)
{
//语句三
}
}
时间复杂度为O(N)
当N趋近于无穷,系数的影响可以忽略不计,因此不带系数
常数次为O(1)
示例1.3:
int fun(int N)
{
for(int i=0;i<10;i++)
{
//语句三
}
}
时间复杂度为N(1)
这里的1不是指一次,而是常数次
2.3示例
示例2.1
const char * strchr ( const char * str, int character );
strchr为字符查找函数,作用是在字符串str中寻找目标字符character
查找次数:
| 最好 | 平均 | 最坏 |
|---|---|---|
| 1次 | N/2 次 | N次 |
当情况不唯一时,选最坏的情况,
即时间复杂度为O(N),这样可以保证任何情况都能满足预期
示例2.2
冒泡排序:
| 最好 | 最坏 |
|---|---|
| N次 | N*N/2 次 |
在冒泡排序前,我们并不知道数组有序无序,因此最好需N次
而最坏需N+(N-1)+(N-2)+...+2+1 == N*N/2次
因此,时间复杂度为O(N^2)
示例2.3
二分查找:
| 最好 | 最坏 |
|---|---|
| 1次 | log2N 次 |
时间复杂度为O(logN)
注:在时间复杂度中,由于log2N不好打,因此常用
logN代替
对二分查找,只需几组数据就能体会其优越性:
| N | 1000 | 100万 | 10亿 |
|---|---|---|---|
| 大概的执行次数 | 10次 | 20 次 | 30次 |
如果将全中国人的信息排好序放入数组,给出一个身份证号码,最多只需31次即可找到那个人的信息。
但二分查找实用性却不强,因为使用其的前提是有序数组
因此,在生活中,用得更多的是红黑树,即一种自平衡二叉查找树
示例2.4
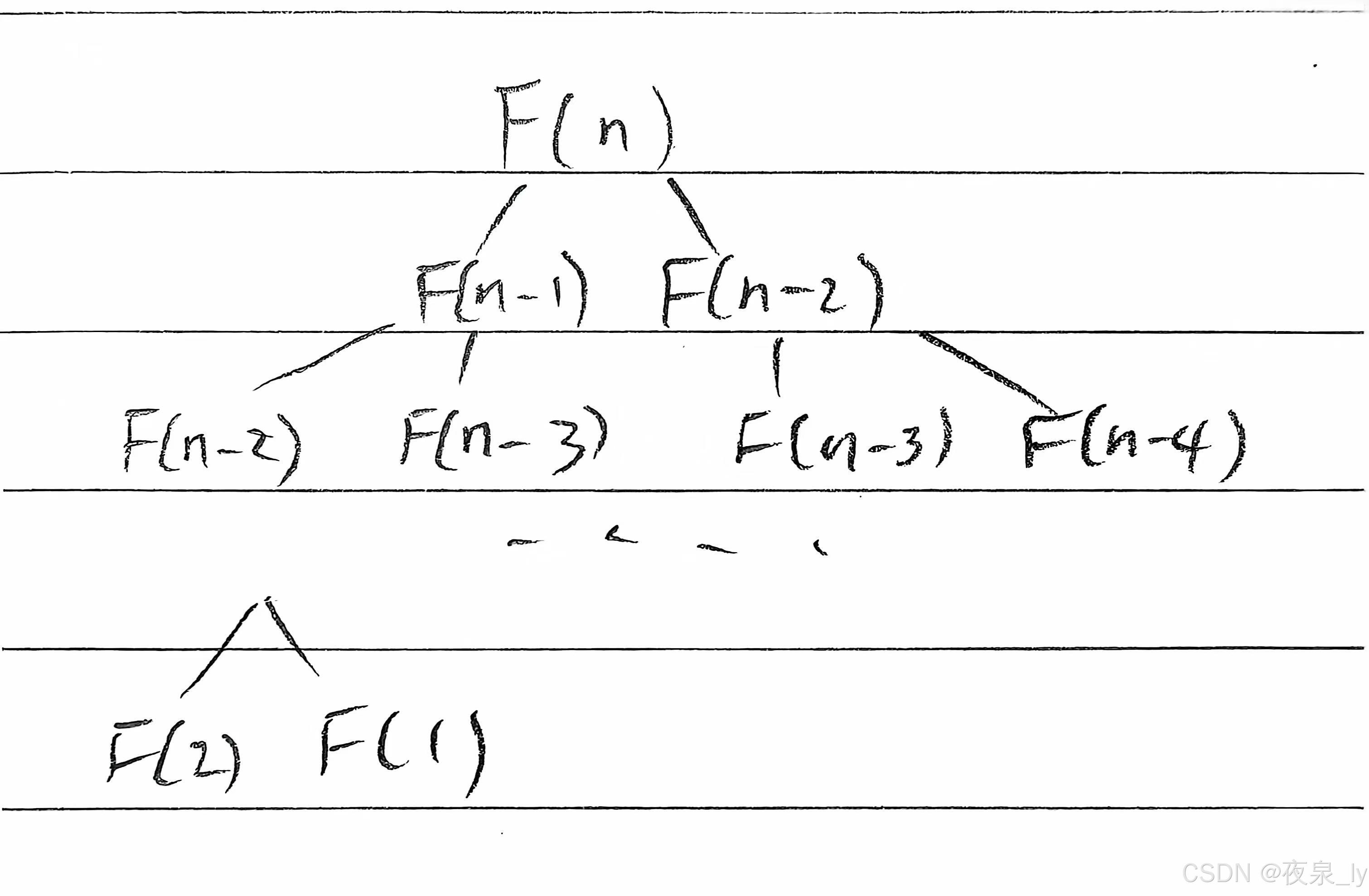
斐波拉契数列的递归写法:
时间复杂度为O(2^N)
| N | 10次 | 20 次 | 30次 |
|---|---|---|---|
| 大概的执行次数 | 1000 | 100万 | 10亿 |
这与二分查找处于两个极端,即较少数据就需大量的计算,因此极不推荐使用
2.4题目
题目描述:数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?
示例 1:
输入:[3,0,1]
输出:2
示例 2:
输入:[9,6,4,2,3,5,7,0,1]
输出:8
法一:
为了做这道题,我首先想到先排序在查找,即使用qsort,但很遗憾,qsort的时间复杂度为O(N*logN)
法二:
异或
int missingNumber(int* nums, int numsSize)
{
int ret=0;
for(int i=0;i<numsSize;i++)
{
ret^=nums[i];
}
for(int i=0;i<=numsSize;i++)
{
ret^=i;
}
return ret;
}
时间复杂度O(N)
思路:a^a=0、a^0=a,因此,ret分别异或数组各元素,并分别异或0~N,得消失的数字
法三:
公式
int missingNumber(int* nums, int numsSize)
{
int ret=0;
int i=0;
for(i=0;i<numsSize;i++)
{
ret+=(nums[i]-i);
}
return i-ret;
}
时间复杂度O(N)
思路:计算0~N的总和,减去数组元素总和,得消失的数字
3.空间复杂度
3.1是什么
前面我讲到了时间复杂度,它是一个算法运行时,大概的基本操作的执行次数。
与此相应,空间复杂度并非指算法运行时所占空间具体大小,如几个比特、几个字节,而指所额外创建的变量个数。
3.2大O符号
这里的大O符号,与时间复杂度中的用法完全一致,遵循一下三点:
- 仅保留最高阶项
- 不带系数
- 常数次为 O(1)
3.3示例
示例1
冒泡排序:
在冒泡排序中,更多的是在循环、比较、交换,而未创建新的数组。
为了执行循环、交换,创建了常数个变量,因此,空间复杂度为N(1)。
这也意味着无论输入数组的大小如何,所需的额外空间都是固定的。
示例2
打印斐波拉契数列前N项:
为了打印前N项,必须能够储存这些信息,可创建元素个数为N的数组。
数组的大小直接与输入 N 相关,空间复杂度为O(N)。
示例3
递归求阶乘:
求阶乘的递归方法中,通过函数调用函数、N不断变小,最终返回N!。
在此过程中,在函数中只进行了判断、调用、返回等操作,未创建额外的变量。
但,函数在调用时会创建其函数栈帧,每个函数栈帧占常数个空间。
因此,空间复杂度为O(N)。
示例4
斐波拉契数列递归求第N项
当使用了递归,就意味着会创建新的函数栈帧。
此处,递归写法中,每个函数栈帧未创建额外的变量,占常数个空间。
因此,空间复杂度取决于最多的、同时创建的函数栈帧数量。
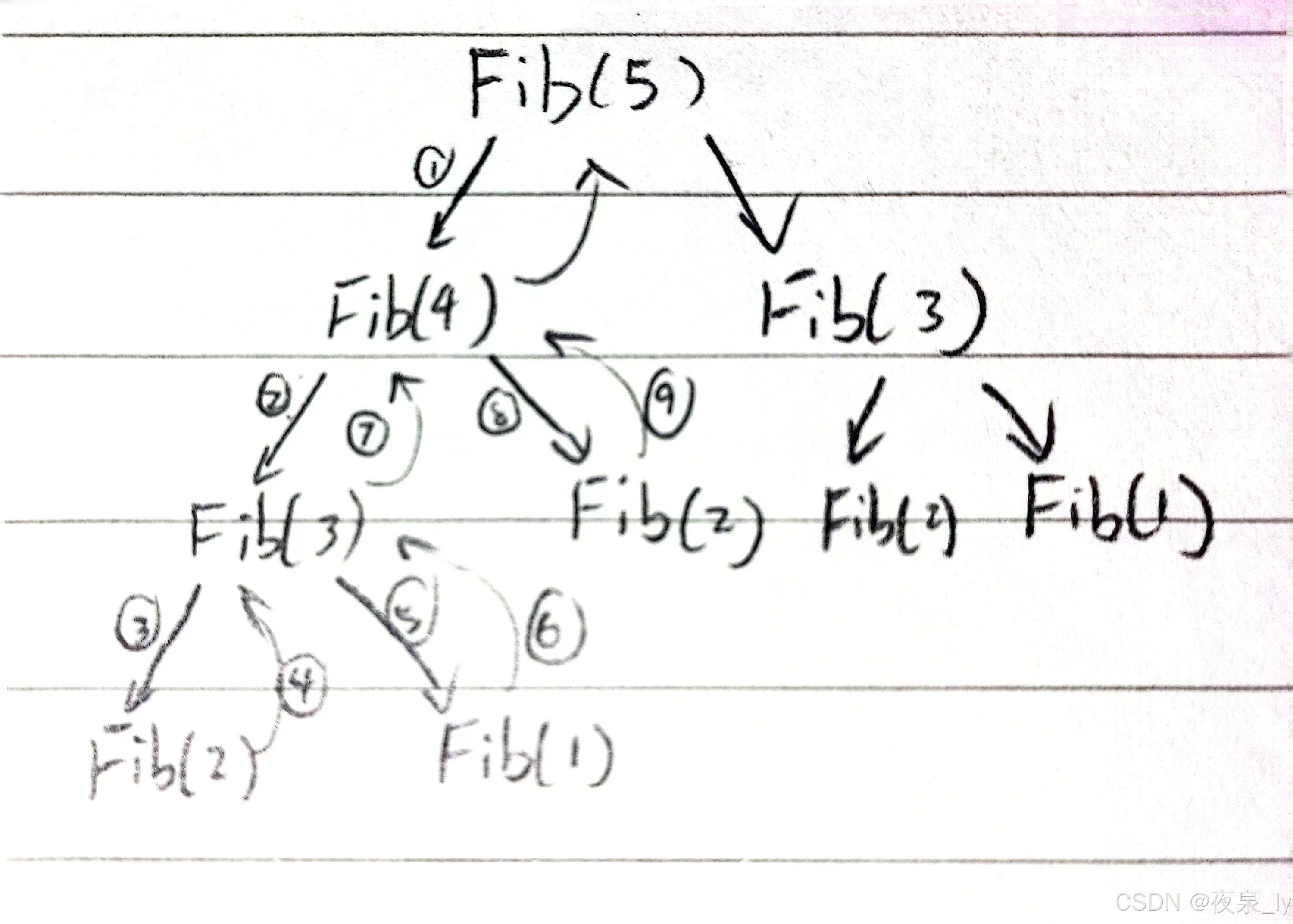
需明确,在遇到return Fib(n-1)+Fib(n-2),首先执行的是Fib(n-1)。
对N=5的情况,可得下图:
可见,最多的、同时创建的函数栈帧数量为N-1。
空间复杂度为O(N)。
4.题目类型
平常做题时,大多会遇到两种类型,这里略做介绍:
IO型
由scanf拿输入条件,由printf打印输出结果,写的是完整程序。
接口型
输入条件为参数,由返回值返回结果,目的是实现一个函数,写的是部分程序。
本文示例中代码部分较少,很多只给了思路,而未给具体代码,
因为我认为,想求复杂度,最好的方法不是死盯代码,而是画、想。
希望本篇文章对你有所帮助!并激发你进一步探索数据结构和算法的兴趣!
本人仅是个C语言初学者,如果您有任何疑问或建议,欢迎随时留言讨论!让我们一起学习,共同进步!