数据结构树1

前言

一，树的引论

二，二叉树

三，二叉树的详细理解

为什么指针按值传递不会修改 root->left？

查到最值的功能

总结

前言

当我们运用链表，栈，队列等线性数据结构来进行搜索数据的时候，他们的时间复杂度都是O(n)，我们不妨做一个小小的测试
假设我们的一个机器可以做一百万次比较每秒
则我们的机器可以执行10^7比较
也就是每次的比较时间为10^-7秒

以上是我们假设一个机器可以做出查找操作的效率，接下来我们用这个机器放入到日常工作中，我们来看看情况，如今我们的数据量是十分惊人的，有着1亿或者10亿的数据量，我们计算一下这个机器处理10亿个数据的效率，运用链表，栈，队列这种数据结构来进行，时间复杂度为O(n)

计算：10亿个数据，我们最差的为10^10*10^-7=10^3s=16.7min，当然我们如果出现了16.7min，肯定是不行的，因为我们都想快点找到自己的数据，所以我们接下来就讲讲树这个结构

一，树的引论

目前我们所学习了链表，栈，队列这些都是线性结构或者说顺序结构

数据结构的选取

有了这么多的数据结构，我们该怎么选择呢？我们应当考虑以下几个方面

1，我们要选择什么样的数据类型

2，操作的成本

3，内存的消耗

4，数据结构实现的难度

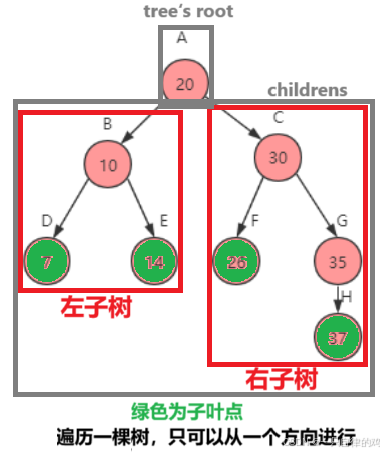
树用于表示一种层次的数据结构
（tree）

树的基本结构介绍

树也可以被称为一个递归的数据结构
（树的基本实现方法就是递归）

这里的子树可以看成递归的深度，这个root为入口

树边的计算

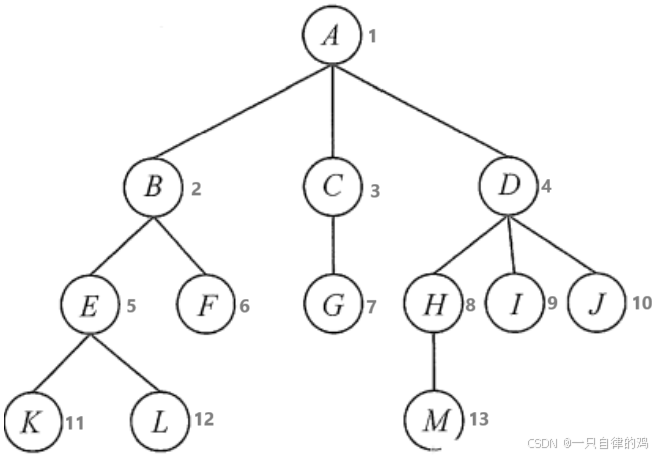
一棵树有N个节点，那么这个树有N-1个节点(图中的每一个线可以表示一个链接或者一个边)，除了根节点外，图中的每一个节点都有一个边进行对应

深度与高度

深度

节点到根节点的路径长度

高度节点到子叶节点的路径长度

7 高度为0，深度为2
5 高度为1，深度为2
13 高度为0，深度为3

总的来说，深度为节点往根节点数，高度为节点往子叶节点数

二，二叉树

二叉树的概念

树上的节点最多只可以有两个子叶节点
（不会超过两个小孩，为左孩和右孩）

我们把我们的树换一个角度思考，换成我们所熟悉的样子来看待问题，这样我们就可以构想出一棵树是如何用我们所学过的知识来转化的，我们树中的孩子节点可以这样设置
struct BstNode {
	int data;
	BstNode* left;
	BstNode* right;
};
基于树的应用

1，存储天然具备的层级的数据结构----电脑上面的磁盘驱动器上的文件系统

2，组织数据----在一个结构里面进行快速的查找与删除，二叉搜索树

3，Trie树----用于字典，用于一个动态的拼写检查

三，二叉树的详细理解

树的类型与属性

二叉树的通用属性：二叉搜索树的每一个节点的子节点不可以超过两个节点

严格二叉树: 每一个二叉树的子节点只可以为0个或者2个

完全二叉树：除了最后一层，其他层填满，并且最后一层的节点全部都是向左靠

这个就是一个完全二叉树的例子

完美二叉树：所有层都填满

二叉树里的计算

1，节点的最大数量：2^0+2^1+2^2+……+2^n=2^(n+1)-1

2，n个节点的完美二叉树的高度：n=2^(h+1)+1 h= $\log_{2}(n+1)$ -1

3，n个节点的完全二叉树的高度：h= $\log_{2}n$ 也就是说时间复杂度为O( $\log_{2}n$ )

4，n个节点的最大高度为（n-1）

所以我们一般把树的高度控制到最小，然后如果只有根节点高度为0，如果没有节点的话就是-1

5，diff=|lhight - rhight| lhight为左子树，rhight为右子树

实现可以用数组也可以用链表

四，二叉搜索树

二叉搜索树是一种可以高效进行搜索和更新的数据结构

之前数据结构的效率

抛问：你该使用什么数据结构进行存储一个可以修改的集合

搜索插入删除类型
O(1) O(1)数组末尾 O(n) 数组

O(n)

O(1)链表头部
O(n) 链表

根据我们的前言可以知道，我们利用这两个类型不用什么好的方法的话，那么时间会花费的非常长，这个时候我们可以考虑用二分法，在两边分别放一个指针，这样我们的时间复杂度就是O( $\log_{2}n$ )了，我们利用这个来看看我们在实际的时候，这个时间复杂度可以减多少呢？

例子

假设我们有2^31的数据量，这个数据量以及超过了20亿的数据量

n=2^31 则时间为31*10^-6秒，这个时间相比较上面那一个以及少量非常多的时间了

二叉树的查找成本为O( $\log_{2}n$ )但是也有很差的情况O(n)，但是这种情况是可以避免的，可以利用平衡二叉树

平衡二叉树的概念

平衡二叉树是一种自平衡的二叉搜索树，其中每个节点的左右子树的高度差（平衡因子）不超过1，这意味着树在任何时候都保持相对平衡的状态，避免了二叉树退化为链表的情况，从而确保了操作的时间复杂度

二叉搜索树
核心规则：
左子树的节点值小于当前节点的值
右子树的节点值大于当前节点的值
左右子树本身也必须是二叉搜索树

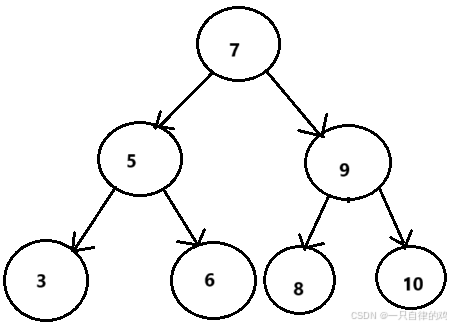
这个是一个二叉搜索树，我们来详细分析一下

5比7小 9比7大，符合
3比5小，比7小 6比5大，比7小 8比9小，比7大 10比9大，比7小符合
我们看这些是要进行比较的，而不是单单比较5和9，左右子树本身也必须是二叉搜索树

五，二分法与二叉搜索树的效率

我们不妨想想，二分法的时间复杂度是多少呢？如果忘记了二分法也没事，我写了一个很简单的二分法代码

二分法
#include<iostream>

using namespace std;

int search(int arr[], int sign, int n, int left, int right) {
	while (left <= right) {
		int mid = left + (right - left) / 2;

		if (arr[mid] == sign) {
			return 1;
		}

		else if (arr[mid] > sign) {
			right = mid - 1;
		}
		else {
			left = mid + 1;
		}
	}
	return -1;
}

int main() {
	int arr[9] = { 1,2,3,4,5,6,7,8,9 };
	int sign = 8;
	int n = sizeof(arr) / sizeof(arr[0]);
	int result = search(arr, sign, n, 0, n - 1);
	if (result == -1) {
		cout << "未找到" << endl;
	}
	else {
		cout << "找到了" << endl;
	}
	return 0;
}
我们在使用二分法的时候，都是利用空间减半的方法，n->n/2->n/4->……，最后找到我们所想要的最终元素，如果没有找到则会left>right的情况，这个就可以判断是否要终止程序

n/2^k => 2^k = n => k = $\log_{2}n$

二叉搜索树

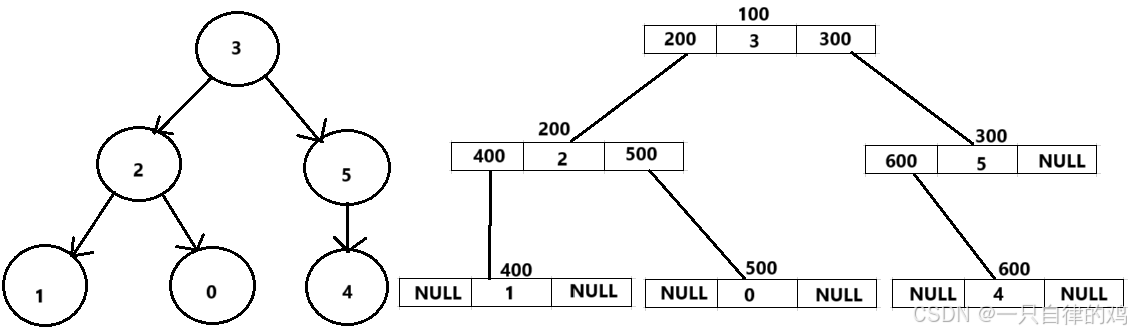
其实你可以发现二叉搜索树也利用了这样的原理，我们可以来研究一下

我们要寻找3这个元素，首先在根部进去进行寻找，然后进行分区，是比7大还是比7小，然后进行对空间的对半分，这不就是二分法么，基于这个思想，我们都很喜欢完美二叉树的出现，为什么呢？这不就是每一次分开的时候，都是对半分，这样效率特别高

我们这里思考了查找，但是我们还要有插入，删除的操作，那我们就需要思考怎么插入或者删除之后，把树平衡起来

六，二叉搜索树的实现

基本实现
#include<iostream>

using namespace std;

struct BstNode {
	BstNode* left;
	int data;
	BstNode* right;
};

BstNode* GetNode(int x) {
	BstNode* newNode = new BstNode();
	newNode->data = x;
	newNode->left = NULL;
	newNode->right = NULL;
	return newNode;
}

BstNode* Insert(BstNode* root, int x) {
	if (root == NULL) {
		root = GetNode(x);
		return root;
	}
	else if (x > root->data) {
		Insert(root->right, x);
	}
	else if (x < root->data) {
		Insert(root->left, x);
	}
	return root;
}

bool search(BstNode* root,int x) {
	if (root == NULL) {
		return false;
	}
	else if (root->data == x) {
		return true;
	}
	else if (root->data >= x) {
		return search(root->left, x);
	}
	else {
		return search(root->right, x);
	}
}

int main() {
	BstNode* root = NULL;
	root = Insert(root, 10);
	root = Insert(root, 6);
	root = Insert(root, 7);
	bool key = search(root, 10);
	if (key == true) {
		cout << "找到了" << endl;
	}
	else {
		cout << "未找到" << endl;
	}
}
这里是用写了插入和搜索，这个main函数里面一定要用root来接收，因为root在其他地方为形参，改变不了形参，如果不想这么麻烦也可以设置一个全局变量，我们重点来理解一下这个递归，我们理解了插入的递归，这个搜索也是可以迎刃而解

细讲递归操作
BstNode* Insert(BstNode* root, int x) {
	if (root == NULL) {
		root = GetNode(x);
		return root;
	}
	else if (x > root->data) {
		Insert(root->right, x);
	}
	else if (x < root->data) {
		Insert(root->left, x);
	}
	return root;
}
这里一开始root肯定是为空的，所以我们要给根节点赋予一个节点，然后下一次的时候就是判断这个节点是放到左子树还是右子树，我们这里用递归来进行树的深入

到了下一次，我们就会到左子树还是右子树，注意此时进入递归了，这个root不是你根节点了，是左子树或者右子树的根节点，然后当我找到left或者right为NULL的时候，我可以用第一个if语句给这个节点赋予一个节点了，重中之重此时的root不是根节点，然后赋予完返回根节点

然后进入到上一次的递归进行返回，最终递归逐个破解，返回的是这个树的根节点

很好这里讲的是错误的，这是作者初代代码，后面有正确的改进，也可以给读者看看错误的递归思路，确实有点绕，此代码也有细小的问题，读者可以先自己思考哪里错误，后面再看正确的思路

放到堆和栈的策略

这个就涉及大到一个变量的生命周期的问题了，大致就是你想临时的就放到栈里，你想长期的就放到堆里

七，查找最大值和最小值

这个十分的简单哈，真的，你会发现这个最大值不就是最右边的那个么，这个最小值不就是最左边那个么，我们来实现一下
#include<iostream>

using namespace std;

struct BstNode {
	BstNode* left;
	int data;
	BstNode* right;
};

BstNode* GetNode(int x) {
	BstNode* newNode = new BstNode();
	newNode->data = x;
	newNode->left = NULL;
	newNode->right = NULL;
	return newNode;
}

BstNode* Insert(BstNode* root, int x) {
	if (root == NULL) {
		root = GetNode(x);
		return root;
	}
	else if (x > root->data) {
		root->right = Insert(root->right, x);
	}
	else if (x < root->data) {
		root->left = Insert(root->left, x);
	}
	return root;
}

bool search(BstNode* root,int x) {
	if (root == NULL) {
		return false;
	}
	else if (root->data == x) {
		return true;
	}
	else if (root->data >= x) {
		return search(root->left, x);
	}
	else {
		return search(root->right, x);
	}
}

BstNode* MAX(BstNode* root) {
	if (root == NULL) {
		cout << "未找到" << endl;
		return NULL;
	}
	BstNode* current = root;
	while (current -> right != NULL) {
		current = current->right;
	}
	return current;
}

int main() {
	BstNode* root = NULL;
	root = Insert(root, 10);
	root = Insert(root, 6);
	root = Insert(root, 7);
	root = Insert(root, 15);
	root = Insert(root, 14);
	root = Insert(root, 20);
	bool key = search(root, 7);
	if (key == true) {
		cout << "找到了" << endl;
	}
	else {
		cout << "未找到" << endl;
	}
	cout << MAX(root)->data << endl;
}
这里是既有修正的代码和寻找最值的代码，我会一一讲述

错误的点
BstNode* Insert(BstNode* root, int x) {
	if (root == NULL) {
		root = GetNode(x);
		return root;
	}
	else if (x > root->data) {
		root->right = Insert(root->right, x);
	}
	else if (x < root->data) {
		root->left = Insert(root->left, x);
	}
	return root;
}
这里为什么不可以利用root = GetNode(x);来给左边和右边进行赋值呢？

假设你插入 6 到如下 BST：
    10
   /  \
 NULL  NULL
执行：
root = Insert(root, 6);
Insert(root, 6);

root = 10
6 < 10，调用 Insert(root->left, 6);
Insert(root->left, 6);
root->left == NULL，进入：
if (root == NULL) {
    root = GetNode(x);  // root 现在指向了新节点 6
    return root;
}
但 root 是 局部变量，修改 root 不会修改 root->left，这里不可以进行对于左边的赋值操作
这一步返回了新节点 6，但 Insert(root->left, 6); 的返回值被丢弃了，没有赋值给 root->left
递归结束后，原来的 root->left 仍然是 NULL，导致插入失败
但是又想，奇怪，我传的是指针呀，为什么是值操作嘞？

指针传递 vs 传引用

在 C++ 里，指针本身是 按值传递 的
换句话说，Insert(root->left, x); 传递的 root->left 是它的拷贝，而不是原始变量的引用
Insert(root->left, x);  // 你以为 root->left 会被修改
我觉得 root->left 传递给 Insert 后，在 Insert 内部的 root = GetNode(x); 可以直接修改 root->left

实际发生的情况：
void Insert(BstNode* root, int x);
root->left 的值（即 NULL）被传递给 Insert
进入 Insert(root->left, x);，这里的 root 只是 root->left 的拷贝
root = GetNode(x); 只是修改了 拷贝的 root，不会修改 root->left
递归结束后，root->left 仍然是 NULL

为什么指针按值传递不会修改 root->left？

来看一个简单的示例
void ChangePointer(int* ptr) {
    ptr = new int(10);  // 只修改了 ptr 的拷贝
}

int main() {
    int* p = NULL;
    ChangePointer(p);
    cout << p << endl;  // 还是 NULL，没有变！
}
这里的 ChangePointer(p); 不会修改 p，因为 p 作为参数传进去时，只是它的拷贝，所以 ptr = new int(10); 不会影响外部的 p

这里也就是我们很常见的指针问题，我们这放了个形参，但不是全局变量，是局部的，这里确实再堆里面创建了一个节点，但是没有东西接收，所以会为NULL，上面这个简单的例子就阐明了

查到最值的功能
BstNode* MAX(BstNode* root) {
	if (root == NULL) {
		cout << "未找到" << endl;
		return NULL;
	}
	BstNode* current = root;
	while (current -> right != NULL) {
		current = current->right;
	}
	return current;
}
我们这里只需要一直往右边就可以找到最大值了

总结

我们总结一下我们所学的东西

1，树的概念和树的基本知识

2，树的高度为节点到子叶的距离，深度为节点到根部的距离

3，二叉树的概念，需注意核心规则

4，二叉树的分类：严格二叉树，完全二叉树，完美二叉树，平衡二叉树

5，二叉树与二分法的关系和两个的具体实现

6，实现的时候遇到了一个bug为指针传递和传引用的区别，两个是不一样的传指针其实也就是一个形参罢了，引用不一样，这个是再原来的地方做法，也就是再常量区，这个需要学过C++才知道

7，查找最值的方法