前言:这是一个刷题系列,如果有错误的地方,或者有更好的解法,欢迎uu们评论。
C题系列 --- 不属于C初阶系列的范畴
目录👉
一、正三角形的打印
1、分解目标1:先定义n = 4(从确定的层数n开始)
2、分解目标2:先打印“排头的空格”
3、 分解目标3:后打印“*”
4、分解目标4:将n改成任意输入
二、杨辉三角的实现
1、分解目标1:把数据输入到数组中
2、分解目标2:打印空格(//详见上文“正三角形的打印---空格的打印”。)
3、分解目标3:打印数组中的数据
4、分解目标4:改变层数,多次调试
一、正三角形的打印
效果展示:👉
6 //输入一个数 ---表示层数
*
* *
* * *
* * * *
* * * * *
* * * * * *思考:整个正三角形的打印貌似可以看作两个三角形的打印。一个是“空格”组成的直角三角形,一个是 * 组成的直角三角形。那为什么 * 变成了正三角形呢?————>被空格“挤”过去的,哈哈。
- 总目标:输入层数n,打印一个n层的正三角形
- 分解目标1:先定义n = 4(从确定的层数n开始)
// " *"
// " * *"
// " * * *"
// "* * * *"
- 分解目标2:先打印“排头的空格”
// " " 👉(n - 1)个空格
// " " 👉(n - 2)个空格
// " " 👉(n - 3)个空格
// "" 👉(n - 4)个空格
// 注意规律:第i行有(n - i)个空格
- 分解目标3:后打印“*”
//注意规律:第i行有i个*
- 分解目标4:将n改成任意输入
1、分解目标1:先定义n = 4(从确定的层数n开始)
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
int n = 4;
return 0;
}2、分解目标2:先打印“排头的空格”
// " " (n - 1)个空格
// " " (n - 2)个空格
// " " (n - 3)个空格
// "" (n - 4)个空格
由于空格的打印有列的控制,还有行的打印(注意规律<如上>),所以空格的打印采用循环的嵌套。
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
int n = 4;
int i = 0;
for (i = n; i > 0; i--)
{
int j = 0;
for (j = i - 1; j > 0; j--)
{
printf(" ");
}
printf("*");//此处*为参照物,用于显示空格的存在
printf("\n");
}
return 0;
}运行结果:👉
*
*
*
*
3、 分解目标3:后打印“*”
//注意规律:第i行有i个*
发现:
第一行----三个空格和一个*
第二行----两个空格和两个*
第三行----一个空格和三个*
······
第 k 行----(i - 1)个空格和k个*
所以,发现空格数与*数的和总是等于4,即层数n
所以,层数减空格数即为该行中*的个数👉 *的个数k = n - (i - 1)
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
int n = 4;
int i = 0;
for (i = n; i > 0; i--)
{
int j = 0;
for (j = i - 1; j > 0; j--)
{
printf(" ");
}
int k = 0; //k = n - (i - 1)---层数减空格数即为该行中*的个数
for (k = n - (i - 1); k > 0; k--)
{
printf("* ");
}
printf("\n");
}
return 0;运行结果👉
4
*
* *
* * *
* * * *4、分解目标4:将n改成任意输入
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
for (i = n; i > 0; i--)
{
int j = 0;
for (j = i - 1; j > 0; j--)
{
printf(" ");
}
int k = 0;
for (k = n - (i - 1); k > 0; k--)
{
printf("* ");
}
printf("\n");
}
return 0;
}👉正三角形最终成果展示:
6
*
* *
* * *
* * * *
* * * * *
* * * * * *二、杨辉三角的实现
- 总目标:打印一个10层以内的任意层数的杨辉三角
- 分解目标1:把数据输入到数组中(先控制层数为5 --- 小一点,便于发现错误)
//由于数组的大小通常不能用变量表示(C99之后才可以),错误案例如下:
错误案例 int n = 0; scanf("%d",&n); int arr[n] = {0};//所以,我这边用的是define定义的标识符常量。
- 分解目标2:打印空格
//详见上文“正三角形的打印---空格的打印”。
- 分解目标3:打印数组中的数据
//注意控制间距,提升观感。
- 分解目标4:改变层数,多次调试
//注意控制间距,提升观感。
成果预览:👉
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1
1、分解目标1:把数据输入到数组中
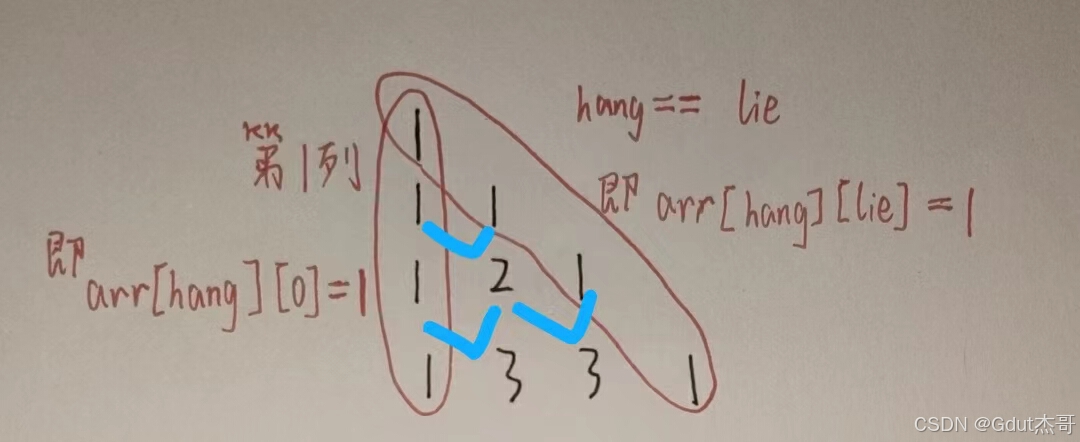
tip:hang ---行 ;lie ---列
杨辉三角数学规律:
tip:设置的变量hang和lie应当从0开始,便于数组数据的遍历
蓝色箭头 --- 代表两数的和等于另一个数
#define n 5
int hang = 0;
int lie = 0;
int arr[n][n] = { 0 };
for (hang = 0; hang < n; hang++)
{
for (lie = 0; lie <= hang; lie++)
{
if (lie == 0 || hang == lie)
{
arr[hang][lie] = 1;
}
else
arr[hang][lie] = arr[hang - 1][lie - 1] + arr[hang - 1][lie];
}
}2、分解目标2:打印空格(//详见上文“正三角形的打印---空格的打印”。)
//由于5层的杨辉三角的数据为都是个位数,所以每次循环选择打印一个空格(控制间距,提升观感)
int i = 0;
for (i = n; i > 0; i--)
{
int j = 0;
for (j = i - 1; j > 0; j--)
{
printf(" ");
}
printf("\n");
}3、分解目标3:打印数组中的数据
//由于5层的杨辉三角的数据为都是个位数,所以选择“ d”,即d的前面一个空格(控制间距,提升观感)
hang = n - i;
lie = 0;
for (lie = 0; lie <= hang; lie++)
{
printf("% d", arr[hang][lie]);
}初步成果展示:👉
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
//输入
#define n 5
int hang = 0;
int lie = 0;
int arr[n][n] = { 0 };
for (hang = 0; hang < n; hang++)
{
for (lie = 0; lie <= hang; lie++)
{
if (lie == 0 || hang == lie)
{
arr[hang][lie] = 1;
}
else
arr[hang][lie] = arr[hang - 1][lie - 1] + arr[hang - 1][lie];
}
}
//输出(打印)
int i = 0;
for (i = n; i > 0; i--)
{
int j = 0;
for (j = i - 1; j > 0; j--)
{
printf(" ");
}
hang = n - i;
lie = 0;
for (lie = 0; lie <= hang; lie++)
{
printf("% d", arr[hang][lie]);
}
printf("\n");
}
return 0;
} 1
1 1
1 2 1
1 3 3 1
1 4 6 4 14、分解目标4:改变层数,多次调试
如果只是把层数n改为10,会怎么样呢?如下:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
歪歪扭扭的,不好看!!!
所以,我们应该去调整间距,最终成果展示:👉
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{
//输入
#define n 10
int hang = 0;
int lie = 0;
int arr[n][n] = { 0 };
for (hang = 0; hang < n; hang++)
{
for (lie = 0; lie <= hang; lie++)
{
if (lie == 0 || hang == lie)
{
arr[hang][lie] = 1;
}
else
arr[hang][lie] = arr[hang - 1][lie - 1] + arr[hang - 1][lie];
}
}
//输出(打印)
int i = 0;
for (i = n; i > 0; i--)
{
int j = 0;
for (j = i - 1; j > 0; j--)
{
printf(" "); //控制空格
}
hang = n - i;
lie = 0;
for (lie = 0; lie <= hang; lie++)
{
printf("%6d", arr[hang][lie]); //控制数据间距
}
printf("\n");
}
return 0;
} 1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1如果有错误的地方,或者有更好的解法,欢迎uu们评论