题目解析

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例 1:

输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3
示例 2:

输入: nums = [4,2,3,4]
输出: 4

解题思路

设三角形三边分别是a,b,c。正常情况下我们需要判断a+b>c,a+c>b,b+c>a，这三种情况。但是如果我们对数组排序使a<=b<<=c。这样我们只需要判断a+b>c即可。例如a=2,b=2,c=3。我们可以判断a+b>c(2+2>3)。当判断a+c>b的时候,由于排序的原因c肯定大于b所以加上了一个a也大于b所以就可以判断出a+c>b。同理可以验证b+c>a。这样一来我们就只需要判断一个条件a+b>c即可。因为有三个变量，所以我们可以先确定一个变量c，再定义两个变量控制a和b，由a+b>c这个条件找到可能的组合。
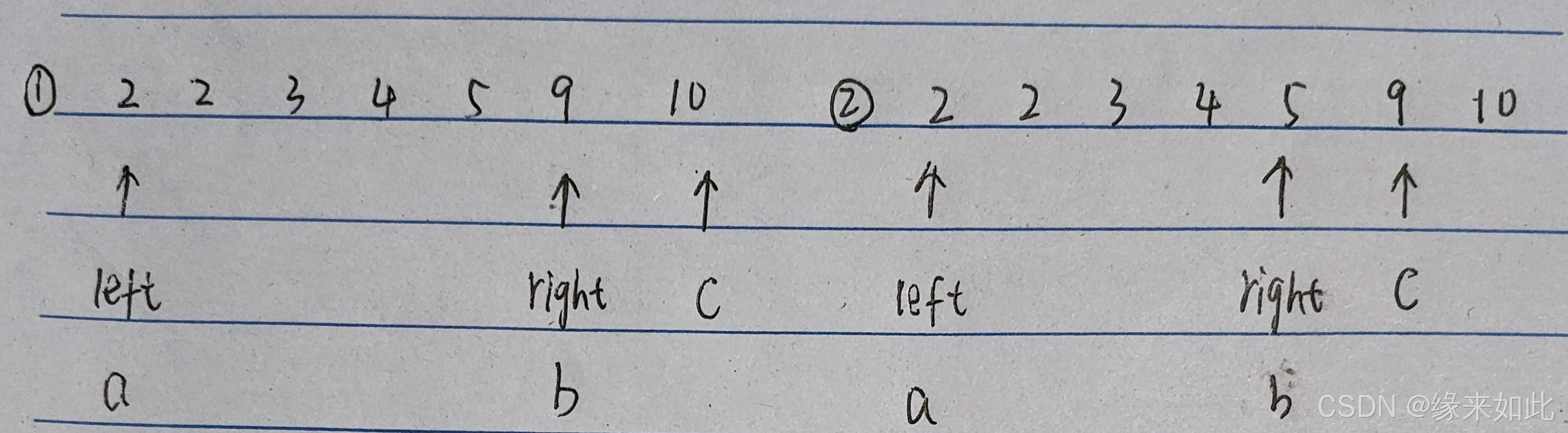
例如在数组arr[2,2,3,4,5,9,10]中

①当a+b>c时,由于排序left向右移动过程中不断更新得到的a+b一定是大于c的。例如: (2、9、10) (2、9、10)(3、9、10)(4、9‘10)(5、9、10)a不断增大所以一定会构成三角形。且种类数量刚好等于(right-left),然后 right–判断下一个区间
②当a+b≤c时, right左移得到a+b一定小于等于C不能构成三角形。
例如(2、5、9) (2、4、9)(2、3、9) (2、2、9),这时left 位置不可取,只需将left++, 判断下一个区间。

代码实现

C语言实现

int compare(void const *str1,void const *str2)
{
	return (*(int*)str1)-(*(int*)str2);
}
int triangleNumber(int* nums, int numsSize) 
{
    qsort(nums,numsSize,sizeof(int),compare);
    int sum=0;
    int left=0;
    int right=0;
    int max=numsSize-1;
    for(max=numsSize-1;max>=2;max--)
    {
		right=max-1;
		left=0;
		while(left<right)
		{
			if(nums[left]+nums[right]>nums[max])
			{
				sum=sum+(right-left);
				right--;
			}
			else
			{
				left++;
			}
		}
	}
	return sum;
}

Java实现

class Solution {
    public int triangleNumber(int[] nums) 
    {
      Arrays.sort(nums);
      int ret=0;
      int n=nums.length;
      for(int i=n-1;i>=2;i--)
      {
        int left=0;
        int right=i-1;
        while(left<right)
        {
            if(nums[left]+nums[right]>nums[i])
            {
                ret+=right-left;
                right--;
            }
            else
            {
                left++;
            }
        }
      }
      return ret;
    }
}

题目链接有效三角形个数
感谢您的阅读，欢迎留言评论。