目录
一、问题描述
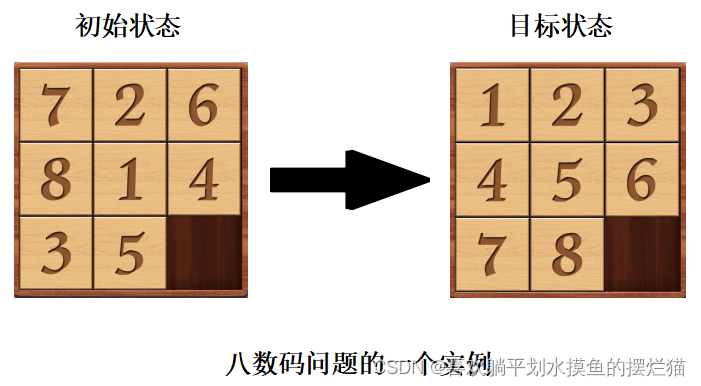
八数码问题是人工智能领域一个经典的问题。也是我们所熟悉的最简单的3×3数字华容道游戏:在一个3×3的九宫格棋盘上,摆有8个正方形方块,每一个方块都标有1~8中的某一个数字。棋盘中留有一个空格,要求按照每次只能将与空格相邻的方块与空格交换的原则,将任意摆放的数码盘(初始状态)逐步摆成某种给定的数码盘的排列方式(目标状态)。
二、涉及算法
启发式搜索又称为有信息搜索,是利用问题拥有启发信息引导搜索,以达到减小搜索范围、降低问题复杂度的目的。在启发式搜索过程中,要对Open表进行排序,这就要有一种方法来计算待扩展结点有希望通向目标结点的不同程度,人们总是希望找到最有可能通向目标结点的待扩展结点优先扩展。一种最常用的方法是定义一个评价函数对各个结点进行计算,其目的就是用来估算出“有希望”的结点。用f来标记评价函数,用f(n)表示结点n的评价函数值,并用f来排列等待扩展的结点,然后选择具有最小f值的结点作为下一个要扩展的结点。
A*算法是一种有序搜索算法,其特点在于对评价函数的定义上。这个评估函数f使得在任意结点上其函数值f(n)能估算出结点S到结点n的最小代价路径的代价与从节点n到某一目标节点的最小代价路径的代价的总和,也就是说f(n)是约束通过结点n的一条最小代价路径的代价的估计。
算法具体内容见文献:
https://wenku.baidu.com/view/4a80a40fa2161479171128de?_wkts_=1713600420821
三、实现步骤
在运行前,需要提前准备好infile.txt文件,第一行规定N的大小,即棋盘的大小,第二行则放置起始状态棋盘中的数字排列,从上往下,从左往右一次排成一列,空格置为0。
1.定义状态结点的类
定义一个State类,主要用于表示搜索过程中的状态结点,包括结点的代价和状态信息,以及结点之间的关系。
属性:
gn:从起始结点到当前结点的实际代价。
hn:从当前结点到目标结点的估计代价(启发式函数)。
fn:综合代价,即gn+hn。
child:子结点列表,存储从当前结点可以到达的所有子结点。
par:父结点,指向生成当前结点的父结点。
state:当前结点的状态矩阵。
hash_value:当前结点状态矩阵的哈希值,用于在查找表中快速查找。
方法:
__lt__:小于运算符重载,用于结点比较。
__eq__:等于运算符重载,用于结点比较。
__ne__:不等于运算符重载,用于结点比较。
class State(object):
def __init__(self, gn=0, hn=0, state=None, hash_value=None, par=None):
self.gn = gn
self.hn = hn
self.fn = self.gn + self.hn
self.child = []
self.par = par
self.state = state
self.hash_value = hash_value
def __lt__(self, other):
return self.fn < other.fn
def __eq__(self, other):
return self.hash_value == other.hash_value
def __ne__(self, other):
return not self.__eq__(other)2.定义曼哈顿距离计算函数
计算两个状态结点之间的曼哈顿距离,作为启发式函数的一部分,用于评估当前结点到目标结点的估计代价。
def manhattan_dis(cur_node, end_node): # 定义一个名为manhattan_dis的函数,接受两个参数cur_node(当前结点)和end_node(目标结点)
# 获取当前结点和目标结点的状态矩阵
cur_state = cur_node.state
end_state = end_node.state
dist = 0
N = len(cur_state) # 获取状态矩阵的大小,假设为N
# 遍历状态矩阵中的每个位置
for i in range(N):
for j in range(N):
# 如果当前结点的值与目标结点的值相等,则跳过当前位置,因为这个位置已经在目标状态中
if cur_state[i][j] == end_state[i][j]:
continue
num = cur_state[i][j] # 获取当前结点在状态矩阵中的值
# 如果当前结点的值为0(空白格),则将目标位置设置为状态矩阵的右下角
if num == 0:
x = N - 1
y = N - 1
# 如果当前结点的值不为0,则根据当前结点的值计算其目标位置,假设目标位置为(x,y)
else:
x = num / N
y = num - N * x - 1
# 计算当前结点与目标位置之间的曼哈顿距离,并累加到总距离中
dist += (abs(x - i) + abs(y - j))
# 返回计算得到的曼哈顿距离作为当前结点到目标结点的估计代价
return dist3.预留占位函数
test_fn是一个占位函数,接受当前结点和目标结点作为参数。目前这个函数没有实际的功能。
def test_fn(cur_node, end_node):
return 04.生成子结点函数
创建generate_child函数,接受当前结点cur_node、目标结点end_node、哈希集合hash_set、OPEN表open_table和距离函数dis_fn作为参数。实现了在当前结点基础上生成可行的子结点,并考虑了重复状态的处理,是A*算法中搜索过程的重要一步。
def generate_child(cur_node, end_node, hash_set, open_table, dis_fn):
# 如果当前结点就是目标结点,则直接将目标结点假如OPEN表,并返回,表示已经找到了解
if cur_node == end_node:
heapq.heappush(open_table, end_node)
return
# 获取当前结点状态矩阵的大小
num = len(cur_node.state)
# 遍历当前结点状态矩阵的每一个位置
for i in range(0, num):
for j in range(0, num):
# 如果当前位置不是空格,则跳过,因为空格是可以移动的位置
if cur_node.state[i][j] != 0:
continue
# 遍历当前位置的四个邻居位置,即上下左右四个方向
for d in direction:
x = i + d[0]
y = j + d[1]
if x < 0 or x >= num or y < 0 or y >=num:
continue
# 记录生成的结点数量
global SUM_NODE_NUM
SUM_NODE_NUM += 1
# 交换空格和邻居位置的数字,生成一个新的状态矩阵
state = copy.deepcopy(cur_node.state)
state[i][j], state[x][y] = state[x][y], state[i][j]
# 计算新状态矩阵的哈希值,并检查是否已经在哈希集合中存在,如果存在则表示已经生成过相同的状态,跳过
h = hash(str(state))
if h in hash_set:
continue
# 将新状态的哈希值添加到哈希集合中,计算新状态结点的gn(从起始结点到当前结点的代价)和hn(当前结点到目标结点的估计代价)
hash_set.add(h)
gn = cur_node.gn + 1
hn = dis_fn(cur_node, end_node)
# 创建新的状态结点对象,并将其加入到当前结点的子结点列表中,并将其加入到OPEN表中。
node = State(gn, hn, state, h, cur_node)
cur_node.child.append(node)
heapq.heappush(open_table, node)5.定义输出路径函数
定义了一个名为print_path的函数,接受一个参数node,表示目标结点。通过回溯父结点的方式,从目标结点一直回溯到起始结点,并将沿途经过的状态矩阵打印出来,以展示搜索路径。
def print_path(node):
# 获取从起始结点到目标结点的路径长度,即目标结点的实际代价
num = node.gn
# 定义了一个内部函数show_block,用于打印状态矩阵
def show_block(block):
print("---------------")
for b in block:
print(b)
# 创建一个栈,用于存储路径中经过的结点
stack = []
# 从目标结点开始,沿着父结点指针一直回溯到起始结点,并将沿途经过的状态矩阵入栈
while node.par is not None:
stack.append(node.state)
node = node.par
stack.append(node.state)
# 从栈中依次取出状态矩阵,并打印出来
while len(stack) != 0:
t = stack.pop()
show_block(t)
# 返回路径长度
return num6.定义A*算法
定义A_start函数,接受起始状态start、目标状态end、距离函数distance_fn、生成子结点函数generate_child_fn和可选的时间限制time_limit作为参数。实现了A*算法的整个搜索过程,包括结点的扩展、路径的搜索和时间限制的处理。
def A_start(start, end, distance_fn, generate_child_fn, time_limit=10):
# 创建起始状态结点和目标状态结点对象,并分别计算其哈希值
root = State(0, 0, start, hash(str(BLOCK)), None)
end_state = State(0, 0, end, hash(str(GOAL)), None)
# 检查起始状态是否就是目标状态,如果是,则直接输出提示信息
if root == end_state:
print("start == end !")
# 将起始状态结点加入到OPEN表中,并对OPEN表进行堆化操作
OPEN.append(root)
heapq.heapify(OPEN)
# 创建一个哈希集合,用于存储已经生成的状态结点的哈希值,并将起始状态结点的哈希值添加到集合中
node_hash_set = set()
node_hash_set.add(root.hash_value)
# 记录算法开始的时间
start_time = datetime.datetime.now()
# 进入主循环,直到OPEN表为空(搜索完成)或达到时间限制
while len(OPEN) != 0:
top = heapq.heappop(OPEN)
# 如果当前结点就是目标状态结点,则直接输出路径
if top == end_state:
return print_path(top)
# 产生孩子节点,孩子节点加入OPEN表
generate_child_fn(cur_node=top, end_node=end_state, hash_set=node_hash_set,
open_table=OPEN, dis_fn=distance_fn)
# 记录当前时间
cur_time = datetime.datetime.now()
# 超时处理,如果运行时间超过了设定的时间限制,则输出超时提示信息并返回
if (cur_time - start_time).seconds > time_limit:
print("Time running out, break !")
print("Number of nodes:", SUM_NODE_NUM)
return -1
# 如果循环结束时OPEN表为空,则表示没有找到路径,输出提示信息并返回-1
print("No road !") # 没有路径
return -17.读取数据作为原始状态
定义read_block函数,接受三个参数block(状态矩阵列表)、line(输入的一行数据)、N(状态矩阵的大小)。将文本数据解析为状态矩阵的形式,并存储在列表中,为后续的状态表示和求解提供原始数据。
def read_block(block, line, N):
# 使用正则表达式提取输入行中的数字数据,并存储在列表res中
pattern = re.compile(r'\d+') # 正则表达式提取数据
res = re.findall(pattern, line)
# 初始化计数变量t和临时列表tmp
t = 0
tmp = []
# 遍历提取的数字数据,将其转换为整数,并添加到临时列表tmp中
for i in res:
t += 1
tmp.append(int(i))
# 当计数变量t达到状态矩阵的大小N时,表示当前行数据处理完毕,将临时表添加到状态矩阵列表中,并清空临时表
if t == N:
t = 0
block.append(tmp)
tmp = []8.定义主函数查看结果
通过主函数if __name__ == 'main'读取输入数据、调用A*算法求解八数码问题,并输出求解结果的相关信息。
if __name__ == '__main__':
# 尝试打开infile.txt文件,如果文件打开失败,则输出错误信息并退出程序
try:
file = open('infile.txt', "r")
except IOError:
print("can not open file infile.txt !")
exit(1)
# 打开名为infile.txt文件,并将文件对象赋值给变量f
f = open("infile.txt")
# 读取文件的第一行,获取棋盘的大小NUMBER
NUMBER = int(f.readline()[-2])
# 根据棋盘大小生成目标状态,并将目标状态存储在列表GOAL中
n = 1
for i in range(NUMBER):
l = []
for j in range(NUMBER):
l.append(n)
n += 1
GOAL.append(l)
GOAL[NUMBER - 1][NUMBER - 1] = 0
# 逐行读取文件中的数据
for line in f: # 读取每一行数据
# 在每次处理新的输入数据之前,需要清空OPEN表和BLOCK表
OPEN = []
BLOCK = []
# 调用读取数据的函数,将当前行的数据解析并存储为状态矩阵
read_block(BLOCK, line, NUMBER)
# 初始化生成的结点数量为0
SUM_NODE_NUM = 0
# 记录算法开始的时间
start_t = datetime.datetime.now()
# 这里添加5秒超时处理,可以根据实际情况选择启发函数
# 将求解路径长度存储在length中
length = A_start(BLOCK, GOAL, manhattan_dis, generate_child, time_limit=10)
# 记录算法结束时间
end_t = datetime.datetime.now()
# 如果找到了路径,则输出路径长度、算法执行时间和生成的结点数量
if length != -1:
print("length =", length)
print("time =", (end_t - start_t).total_seconds(), "s")
print("Nodes =", SUM_NODE_NUM)四、运行结果
A*算法在解决八数码问题中表现出较高的准确性。通过启发式函数曼哈顿距离的计算,能够较准确的评估当前结点到目标节点的代价,并在搜索过程中选择代价最小的路径。通过和实际路径长度的比较,可以验证算法的准确性。
同时,A*算法在搜索过程中充分利用了启发式函数的估计值,能够更优先的扩展可能更接近目标的结点,从而提高搜索效率,但是,在某些复杂的情况下,仍可能耗费较长时间或无法找到解,这取决于问题的复杂度和启发式函数的选择。
以下结果显示的是从初始状态转变成目标状态的一个具体过程。
---------------
[7, 2, 6]
[8, 1, 4]
[3, 5, 0]
---------------
[7, 2, 6]
[8, 1, 0]
[3, 5, 4]
---------------
[7, 2, 0]
[8, 1, 6]
[3, 5, 4]
---------------
[7, 0, 2]
[8, 1, 6]
[3, 5, 4]
---------------
[7, 1, 2]
[8, 0, 6]
[3, 5, 4]
---------------
[7, 1, 2]
[8, 5, 6]
[3, 0, 4]
---------------
[7, 1, 2]
[8, 5, 6]
[0, 3, 4]
---------------
[7, 1, 2]
[0, 5, 6]
[8, 3, 4]
---------------
[0, 1, 2]
[7, 5, 6]
[8, 3, 4]
---------------
[1, 0, 2]
[7, 5, 6]
[8, 3, 4]
---------------
[1, 5, 2]
[7, 0, 6]
[8, 3, 4]
---------------
[1, 5, 2]
[7, 3, 6]
[8, 0, 4]
---------------
[1, 5, 2]
[7, 3, 6]
[8, 4, 0]
---------------
[1, 5, 2]
[7, 3, 0]
[8, 4, 6]
---------------
[1, 5, 2]
[7, 0, 3]
[8, 4, 6]
---------------
[1, 5, 2]
[7, 4, 3]
[8, 0, 6]
---------------
[1, 5, 2]
[7, 4, 3]
[0, 8, 6]
---------------
[1, 5, 2]
[0, 4, 3]
[7, 8, 6]
---------------
[1, 5, 2]
[4, 0, 3]
[7, 8, 6]
---------------
[1, 0, 2]
[4, 5, 3]
[7, 8, 6]
---------------
[1, 2, 0]
[4, 5, 3]
[7, 8, 6]
---------------
[1, 2, 3]
[4, 5, 0]
[7, 8, 6]
---------------
[1, 2, 3]
[4, 5, 6]
[7, 8, 0]
length = 22
time = 0.09839 s
Nodes = 8274
进程已结束,退出代码为 0五、完整代码
import heapq
import copy
import re
import datetime
BLOCK = []
GOAL = []
direction = [[0, 1], [0, -1], [1, 0], [-1, 0]]
OPEN = []
SUM_NODE_NUM = 0
class State(object):
def __init__(self, gn=0, hn=0, state=None, hash_value=None, par=None):
self.gn = gn
self.hn = hn
self.fn = self.gn + self.hn
self.child = []
self.par = par
self.state = state
self.hash_value = hash_value
def __lt__(self, other):
return self.fn < other.fn
def __eq__(self, other):
return self.hash_value == other.hash_value
def __ne__(self, other):
return not self.__eq__(other)
def manhattan_dis(cur_node, end_node):
cur_state = cur_node.state
end_state = end_node.state
dist = 0
N = len(cur_state)
for i in range(N):
for j in range(N):
if cur_state[i][j] == end_state[i][j]:
continue
num = cur_state[i][j]
if num == 0:
x = N - 1
y = N - 1
else:
x = num / N
y = num - N * x - 1
dist += (abs(x - i) + abs(y - j))
return dist
def test_fn(cur_node, end_node):
return 0
def generate_child(cur_node, end_node, hash_set, open_table, dis_fn):
if cur_node == end_node:
heapq.heappush(open_table, end_node)
return
num = len(cur_node.state)
for i in range(0, num):
for j in range(0, num):
if cur_node.state[i][j] != 0:
continue
for d in direction:
x = i + d[0]
y = j + d[1]
if x < 0 or x >= num or y < 0 or y >= num:
continue
global SUM_NODE_NUM
SUM_NODE_NUM += 1
state = copy.deepcopy(cur_node.state)
state[i][j], state[x][y] = state[x][y], state[i][j]
h = hash(str(state))
if h in hash_set:
continue
hash_set.add(h)
gn = cur_node.gn + 1
hn = dis_fn(cur_node, end_node)
node = State(gn, hn, state, h, cur_node)
cur_node.child.append(node)
heapq.heappush(open_table, node)
def print_path(node):
num = node.gn
def show_block(block):
print("---------------")
for b in block:
print(b)
stack = []
while node.par is not None:
stack.append(node.state)
node = node.par
stack.append(node.state)
while len(stack) != 0:
t = stack.pop()
show_block(t)
return num
def A_start(start, end, distance_fn, generate_child_fn, time_limit=10):
root = State(0, 0, start, hash(str(BLOCK)), None)
end_state = State(0, 0, end, hash(str(GOAL)), None)
if root == end_state:
print("start == end !")
OPEN.append(root)
heapq.heapify(OPEN)
node_hash_set = set()
node_hash_set.add(root.hash_value)
start_time = datetime.datetime.now()
while len(OPEN) != 0:
top = heapq.heappop(OPEN)
if top == end_state:
return print_path(top)
generate_child_fn(cur_node=top, end_node=end_state, hash_set=node_hash_set,
open_table=OPEN, dis_fn=distance_fn)
cur_time = datetime.datetime.now()
if (cur_time - start_time).seconds > time_limit:
print("Time running out, break !")
print("Number of nodes:", SUM_NODE_NUM)
return -1
print("No road !")
return -1
def read_block(block, line, N):
pattern = re.compile(r'\d+')
res = re.findall(pattern, line)
t = 0
tmp = []
for i in res:
t += 1
tmp.append(int(i))
if t == N:
t = 0
block.append(tmp)
tmp = []
if __name__ == '__main__':
try:
file = open('infile.txt', "r")
except IOError:
print("can not open file infile.txt !")
exit(1)
f = open("infile.txt")
NUMBER = int(f.readline()[-2])
n = 1
for i in range(NUMBER):
l = []
for j in range(NUMBER):
l.append(n)
n += 1
GOAL.append(l)
GOAL[NUMBER - 1][NUMBER - 1] = 0
for line in f:
OPEN = []
BLOCK = []
read_block(BLOCK, line, NUMBER)
SUM_NODE_NUM = 0
start_t = datetime.datetime.now()
length = A_start(BLOCK, GOAL, manhattan_dis, generate_child, time_limit=10)
end_t = datetime.datetime.now()
if length != -1:
print("length =", length)
print("time =", (end_t - start_t).total_seconds(), "s")
print("Nodes =", SUM_NODE_NUM)