一，基本概念

函数递归指的是在一个函数的定义中使用该函数自身的编程技巧。也就是说，一个函数会直接或间接地调用自己。递归通常包含两个关键部分：

• 递归基（终止条件）：这是递归结束的条件。如果没有终止条件，函数会一直调用自己，最终导致栈溢出错误。终止条件用于确保递归能够在满足特定条件时停止，返回一个确定的结果。
• 递归步骤：函数通过调用自身来解决规模更小的子问题，逐步向终止条件靠近。

递归的工作原理

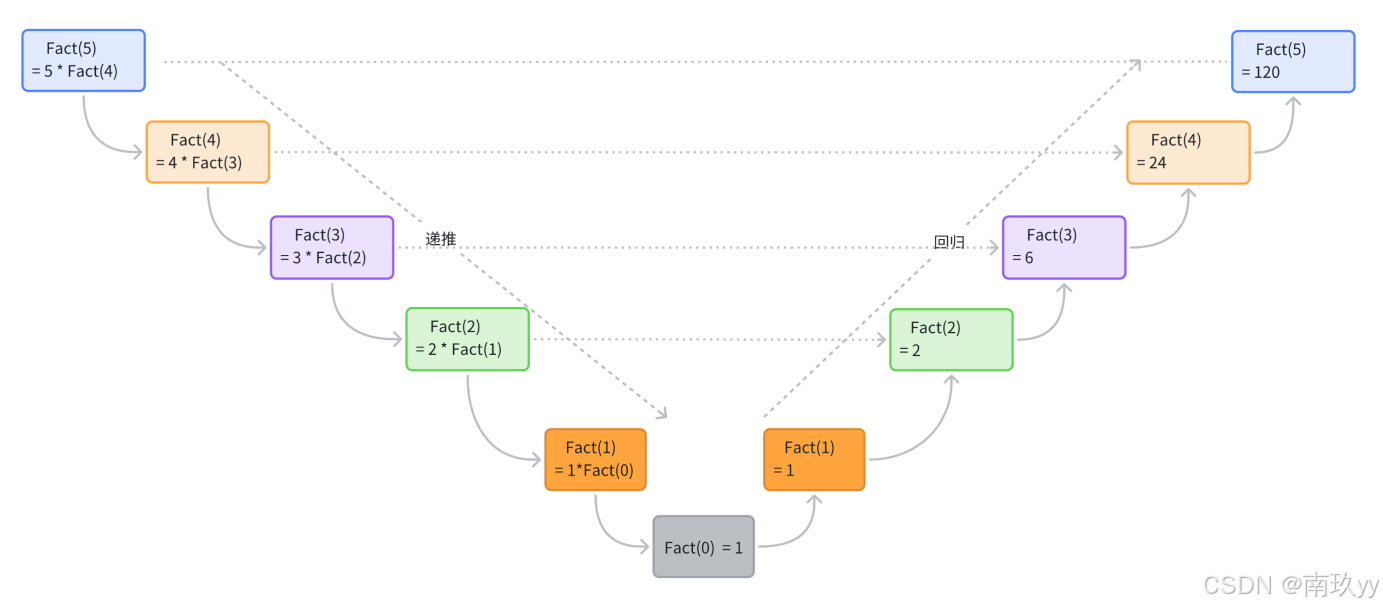
当一个函数调用自身时，系统会为每一次调用创建一个新的函数调用栈帧，栈帧中包含了函数的局部变量、参数以及返回地址等信息。每次递归调用都会将新的栈帧压入栈中，直到满足终止条件。当满足终止条件后，函数开始从最深层的调用逐步返回，依次释放栈帧，直到返回到最初的调用点。

递归的使用场景

• 数学问题：如阶乘、斐波那契数列等问题，这些问题具有明显的递归性质，可以通过递归的方式简洁地解决。
• 数据结构操作：在处理树形结构（如二叉树）、链表等数据结构时，递归可以方便地遍历和操作这些结构。

示例代码

阶乘函数

阶乘的定义为：n! = n * ( n - 1 ) * ( n - 2 ) * `````*1,其中 0! = 1。可以使用递归的方式实现阶乘函数：

#include <stdio.h>

// 递归实现阶乘函数
int Fact(int n) 
{   // 终止条件
    if (n == 0 || n == 1) 
   {
        return 1;
    }
    // 递归步骤
    return n * Fact(n - 1);
}

int main() 
{
    int num = 5;
    int result = Fact(num);
    printf("%d 的阶乘是: %d\n", num, result);
    return 0;
}

在上述代码中，Fact 函数接收一个整数 n 作为参数。当 n 为 0 或 1 时，满足终止条件，函数直接返回 1；否则，函数通过调用 Fact(n - 1) 来计算 n - 1 的阶乘，然后将结果乘以 n 得到 n 的阶乘。

斐波那契数列

斐波那契数列的定义为：F(n) = F(n - 1) + F( n - 2)，其中 F(0) = 0，F(1) = 1。可以使用递归的方式实现斐波那契数列的计算：

#include <stdio.h>

// 递归实现斐波那契数列
int fibonacci(int n)
{
    // 终止条件
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    // 递归步骤
    return fibonacci(n - 1) + fibonacci(n - 2);
}

int main() 
{
    int num = 6;
    int result = fibonacci(num);
    printf("斐波那契数列的第 %d 项是: %d\n", num, result);
    return 0;
}

在上述代码中，fibonacci 函数接收一个整数 n 作为参数。当 n 为 0 时，返回 0；当 n 为 1 时，返回 1；否则，函数通过调用 fibonacci(n - 1) 和 fibonacci(n - 2) 来计算第 n 项的斐波那契数。

注意事项

• 终止条件的重要性：必须确保递归函数有明确的终止条件，否则会导致无限递归，最终耗尽系统栈空间，引发栈溢出错误。
• 性能问题：递归虽然可以使代码简洁易懂，但在某些情况下，递归的性能可能不如迭代。例如，斐波那契数列的递归实现会存在大量的重复计算，时间复杂度为指数级。在对性能要求较高的场景下，需要考虑使用迭代的方式来替代递归。
• 栈空间的使用：每次递归调用都会创建一个新的栈帧，因此递归深度过深时，会占用大量的栈空间。在处理大规模数据时，要注意栈溢出的风险。