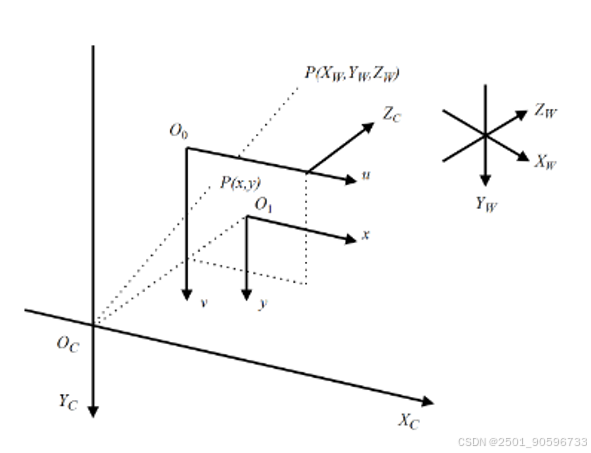
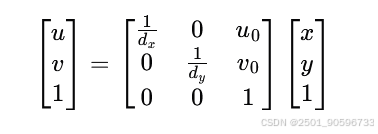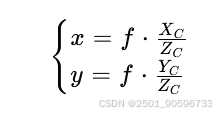2. 双目立体视觉测距原理

 2.1 视觉坐标系

        在双目立体视觉系统进行成像时，核心任务在于把空间中的三维坐标转换为像素坐标。该技术借助相机成像模型，将三维世界里的物体及其对应的二维图像实现映射。通常情况下，这一过程会涉及三个坐标系之间的转换，分别是图像坐标系、相机坐标系以及世界坐标系。其中，图像坐标系主要用来描述像素点在图像中的具体位置，相机坐标系为物体在相机视角下的相对位置和方向，而世界坐标系则表示物体在现实空间里的位置和方向。

（1）图像坐标系

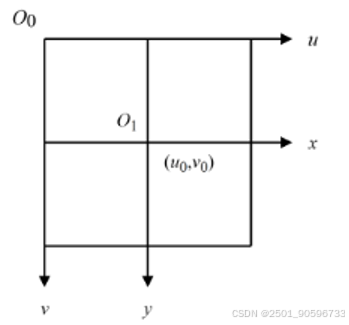
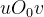
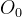
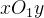
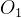
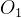
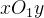
        图像坐标系示意图如下图2.1所示。其中，表示图像平面上的像素图像坐标系，原点为 。在这个坐标系中，u轴和v轴是垂直的，图像上每个像素点的位置可以通过坐标（u,v）来表示。此外，另一个二维直角坐标系，即物理图像坐标系，这个坐标系同样位于图像平面上，其原点为 ，此外， 不仅是坐标系的原点，同时也是相机轴线与图像平面的交点。。

图2.1 图像坐标系

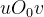
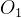
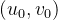
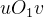
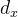
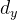
        假设在坐标系中，点的坐标为，坐标系中，每个像素点在x轴方向的长度为个物理单位，在y轴方向上的长度为个物理单位。因此，两个坐标系中的坐标(x,y)和(u,v)之间的关系可以表示为以下形式：

（2）相机坐标系

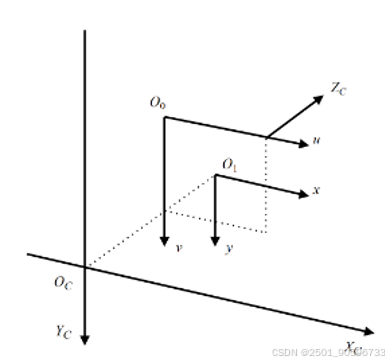
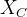
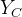
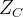
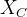
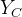
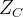
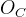
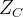
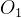
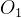
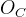
        相机坐标系示意图如下图2.2所示，其中，，为相机坐标系的三个轴，它们彼此之间相互垂直。其中，，轴分别与图像坐标系的x轴和y轴平行， 轴与相机的光轴重合。坐标系的原点为，同时也是相机的光心。轴和相机成像平面在点处相交，和之间的距离即为相机的焦距。

图2.2 相机坐标系

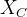
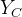
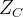
        假设图像坐标中，某一点的坐标为(x,y)，而在相机坐标系中，该点的坐标为(，，​)，相机的焦距记为f，那么图像坐标与相机坐标之间的关系如下式所示：

（3）世界坐标系

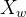
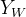
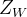
        世界坐标系表示三维世界的真实坐标，包括互相垂直的三个坐标轴，, ，如图2.3所示。

图2.3 世界坐标系

        将某个点从在世界坐标系中的坐标转换为在相机坐标系下的坐标，其方法如下式所示。其中，R表示旋转矩阵，T表示平移变量。

PS:亲爱的读者朋友们，大家好！首先非常感谢您抽出宝贵的时间阅读我的这篇博客。我想在此特别说明一下，这篇博客仅仅是我在个人学习、探索以及实践过程中的一个记录。我深知自己并非该领域的绝对专家，知识水平和实践经验都有限。因此，我不能确保博客中所提及的所有信息、观点和方法都真实和准确。