题目
解法一
求出前缀最大和后缀最大,用两者较小值减去当前高度,累加即可,这个思路容易想到,这里不赘述
class Solution {
public:
int trap(vector<int>& height) {
vector<int> preMx(height.size()), postMx(height.size());
int mx = 0;
for (int i = 0; i < height.size(); i++) {
preMx[i] = mx;
mx = max(mx, height[i]);
}
mx = 0;
for (int i = height.size() - 1; i >= 0; i--) {
postMx[i] = mx;
mx = max(mx, height[i]);
}
int ans = 0;
for (int i = 0; i < height.size(); i++) {
int mi = min(preMx[i], postMx[i]);
if (mi - height[i] > 0) {
ans += mi - height[i];
}
}
return ans;
}
};
解法二
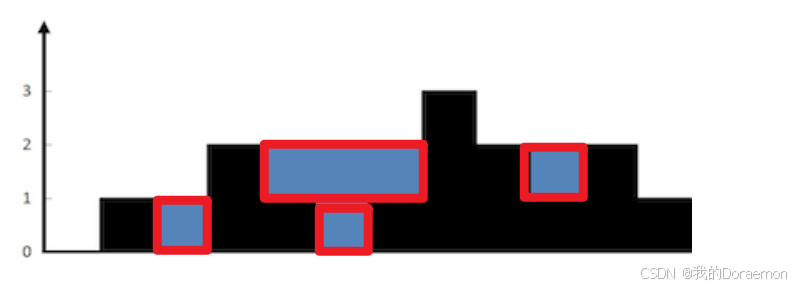
主要学习单调栈的写法,解法一是考虑下竖着计算,计算每个位置的水的高度,而单调栈则是横着计算,如下图:
维护一个栈,满足从栈底到栈顶元素大小递减。如果当前元素高于栈顶,且栈内有至少2个元素,则形成了一个凹槽,及一个图中横着的红色矩形,将它的面积累加即可,第一次写难在维护单调栈中计算面积和。
class Solution {
public int trap(int[] height) {
int[] stack = new int[20010];
int top = -1, ans = 0;
for (int i = 0; i < height.length; i++) {
while (top != -1 && height[i] > height[stack[top]]) {
//高度为(Math.min(height[i], height[stack[top-1]]) - height[stack[top]])
//宽度为(i - stack[top-1] - 1)
if (top >= 1) {
ans += (Math.min(height[i], height[stack[top-1]]) - height[stack[top]]) * (i - stack[top-1] - 1);
}
top--;
}
stack[++top] = i;
}
return ans;
}
}