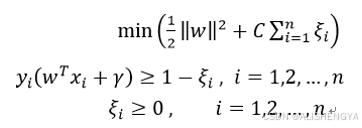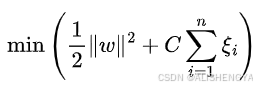支持向量机算法(一):像讲故事一样讲明白它的原理及实现奥秘-CSDN博客一文学习了什么是支持向量机,支持向量机的种类,以及支持向量机中的线性可分支持向量机,本次将学习线性支持向量机。
线性可分支持向量机只能处理线性可分问题,但实际应用中往往均是非线性问题,很难找到一条直线将两个样本完全分开,这时只能通过其他非线性模型或特征升维等技巧得到一个非线性的超平面,但这种在训练集上的优异表现可能会导致过拟合的结果,从而降低模型的泛化能力。
在线性可分支持向量机模型中,样本分类正确要严格满足,称为硬间隔最大化。而在线性支持向量机模型中,可以通过引入松弛因子ξi ≥0,使样本只要满足
时即正确分类。由于每个样本都有一个松弛因子,那些极少数的噪声样本会给予更大的松弛因子以满足正确分类的条件,而对于大部分样本松弛因子ξi ≥0,即可满足正确分类的条件,这种方式即为软件间隔最大化。线性支持向量机的最优化问题形式如下:
☀一看到公式是不是就望而生畏,凡是最怕认真,咱们一个个研究
1、形式最复杂的公式:这是整个优化问题的目标,即要最小化这个表达式的值,min就是这个意思。
(1)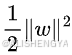
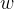
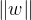
(2)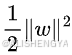
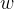
☀那权重向量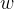
权重向量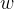
(3)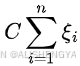
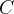
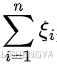
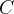
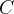
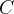
2、约束条件
,这是主要的约束条件。
(1)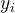
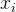
(2)
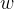
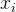
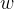
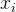
(3)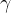
(4)整个式子表示样本
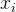
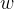
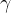
,这意味着样本到超平面的距离足够大,能够很好地被分类。但是由于数据中可能存在噪声等问题,引入了松弛变量ξi,允许一些样本满足
,即这些样本可以在间隔内甚至在超平面的错误一侧,但会受到惩罚(通过目标函数中的
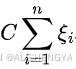
(5):这是对松弛变量的约束,确保松弛变量是非负的,因为它们表示的是距离的调整量,不能为负数。
3、构造拉格朗日函数
线性支持向量机模型的最优化问题求解与线性可分支持向量机类似,构造拉格朗日函数,对每个样本都引入一个拉格朗日乘子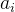
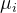
之后与线性可分向量机一样推导出最优化问题的表示,然后使用二次规划算法SMO算法求解得到最优的α值。
☀这个公式里的各个项目都在上面的公式详解中,这儿有两个未出现词,一个是拉格朗日?一个是二次规划算法SMO,那么他们是什么呢?
拉格朗日(Joseph-Louis Lagrange)是一位著名的法国数学家、物理学家,是不是如雷贯耳。
(1)拉格朗日函数是在求解带约束条件的优化问题时引入的一个辅助函数。它将目标函数和约束条件结合在一起,通过引入拉格朗日乘子,将有约束的优化问题转化为无约束的优化问题。
(2)拉格朗日乘子是拉格朗日函数中的参数,它具有一定的物理或几何意义,反映了约束条件对目标函数的影响程度。
(3)SMO(Sequential Minimal Optimization)即序列最小优化算法,是一种用于求解支持向量机(SVM)训练过程中二次规划问题的高效算法。
☀什么是二次规划问题呢?
(1)目标函数:
二次规划问题就像是一场寻找最佳方案的游戏。它的目标函数就好比是一个 “打分机器”,用来给你的方案打分,看看这个方案好不好。这个打分机器有两部分,一部分是和方案的 “规模”(用变量表示)的平方有关的,就像你做一件事,做得越多或者越大,这部分的分数就会按照平方的关系变化;另一部分是和方案的 “规模” 直接相关的分数。
(2)约束条件
但是玩这个游戏是有规则的。约束条件就是这些规则,有“不能超过某个限度”的规则(线性不等式约束),就像你去超市买东西,你的钱是有限的,不能想买多少就买多少;还有“必须正好是某个数量”的规则(线性等式约束),比如你参加一个比赛,规定每个队必须正好有五个人,这就是等式约束;而且每个方案本身也有自己的范围限制,就像比赛的队伍人数不能是负数一样。
至此,线性支持向量的讲解完毕,有不足之处欢迎批评指正,下次将进行非线性支持向量机的学习。