C/DIoU Loss阅读笔记
(一)Title
前言:作者将GIoU的思想进行概括,得到了一个统一的描述框架
L
=
1
−
I
o
U
+
R
(
B
,
B
g
t
)
\mathcal{L}=1-I o U+\mathcal{R}\left(B, B^{g t}\right)
L=1−IoU+R(B,Bgt),并基于该描述框架,提出了DIoU和CIoU,考虑了将中心点距离以及纵横比引入到IoU损失的正则项中。是一篇好文章,如果能够对于CIoU引入的长宽比为什么要采取
v
=
4
π
2
(
arctan
w
g
t
h
g
t
−
arctan
w
h
)
2
v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2}
v=π24(arctanhgtwgt−arctanhw)2这种形式进行说明就更加完美了。
(二)Summary
背景概述
目标检测中的bounding box回归任务往往采取的方式借助损失去回归bounding boxes的参数(位置/长/宽),但是它并不适用于评估度量(Intersection over Union,IoU)。
同时作者指出当前研究者提出的IoU度量(IoU Loss 以及 Generalized IoU Loss)上存在的一些问题:
收敛慢slow convergence
回归不准确,inaccurate regression
主要内容
作者在本文中提出的Distance-IoU(DIoU loss)中通过引入预测box和真实box之间的归一化距离,使得收敛速度加快。并且作者提出的
C
I
o
U
CIoU
CIoU结合了bounding box回归中3个几何因素:overlap area,central point distancce以及长宽比,来达到更快的收敛和更佳的性能,并且DIoUcan be easily adopted into non-maximum suppression(NMS)中。
本文中提出的Distance-IoU(DIoU) loss,具体来说是在IoU Loss损失上增加一个惩罚项,直接最小化两个bounding box中心点之间的归一化距离,从而实现比GIoU更快地收敛。同时作者提出一个好的bounding box回归损失应该考虑到重叠面积,中心点距离以及纵横比,通过结合这些几何度量,作者进一步提出了Complete IoU(CIoU),获得更快的收敛速度以及更好的性能。
主要贡献
- 提出的DIoU,相比于GIoU和IoU Loss具有更快的收敛速度
- 同时考虑重叠面积,中心点距离,以及长宽比这三个几何度量,提出CIoU,能够更快更好地进行bounding box的回归
- 在NMS中使用DIoU,能够提升抑制多余bounding boxes的能力
- 所提出的方法能够结合到最先进的目标检测算法中,实现显著的性能提升。
(三)Research Object
作者将GIoU的思想进行概括,得到了一个统一的描述框架 L = 1 − I o U + R ( B , B g t ) \mathcal{L}=1-I o U+\mathcal{R}\left(B, B^{g t}\right) L=1−IoU+R(B,Bgt),并基于该描述框架,提出了DIoU和CIoU,考虑了将中心点距离以及纵横比引入到IoU损失的正则项中。
(四)Problem Statement
使用IoU Loss无法解决bounding box不存在overlap时的优化问题,而GIoU的回归过程分两个阶段:(1.增加bounding box的面积,2.预测box和目标box存在重叠后利用IoU项进行回归),导致GIoU的收敛比较缓慢,从而引出本文作者提出的两个问题:
- 为了最小化预测box和目标box的归一化距离是否可行?(博主本人关于此内容的猜想是在IoU回归的同时增加一项位置损失)
- 当与目标框有重叠甚至包含时,如何使回归更加准确和快速?
(五)Method
作者将GIoU以及本文的DIoU和CIoU使用统一的形式进行表示:
L
=
1
−
I
o
U
+
R
(
B
,
B
g
t
)
\mathcal{L}=1-I o U+\mathcal{R}\left(B, B^{g t}\right)
L=1−IoU+R(B,Bgt)
其中
R
(
B
,
B
g
t
)
\mathcal{R}\left(B, B^{g t}\right)
R(B,Bgt)表示的是正则化函数,是关于预测box
B
B
B和目标box
B
g
t
B^{gt}
Bgt的函数
Distance-IoU Loss
将正则项定义为:
R
D
I
o
U
=
ρ
2
(
b
,
b
g
t
)
c
2
\mathcal{R}_{D I o U}=\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}
RDIoU=c2ρ2(b,bgt)
其中
b
and
b
g
t
\mathrm{b} \text { and } \mathbf{b}^{g t}
b and bgt分别表示
B
and
B
g
t
B \text { and } B^{g t}
B and Bgt的中心点,
ρ
(
⋅
)
\rho(\cdot)
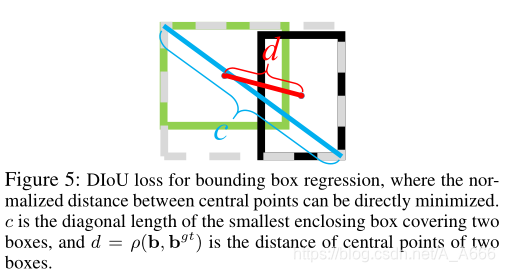
ρ(⋅)表示的是欧拉距离,此处c两个box最小闭包矩形的对角线长度,然后,损失函数就变成了:
L
D
I
o
U
=
1
−
I
o
U
+
ρ
2
(
b
,
b
g
t
)
c
2
\mathcal{L}_{D I o U}=1-I o U+\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}
LDIoU=1−IoU+c2ρ2(b,bgt)
Complete IoU Loss
作者提出一个好的损失应该考虑3个重要的几何因素:重叠面积,中心点距离以及长宽比,通过IoU考虑了重叠面积,通过Distance-IoU的正则项考虑了中心点距离,为了考虑长宽比的影响,作者引入了CIoU
CIoU的正则化项
R
C
I
o
U
=
ρ
2
(
b
,
b
g
t
)
c
2
+
α
v
\mathcal{R}_{C I o U}=\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}+\alpha v
RCIoU=c2ρ2(b,bgt)+αv
其中
α
\alpha
α是一个正的trade-off参数,
v
v
v用于去度量长宽比的一致性
v
=
4
π
2
(
arctan
w
g
t
h
g
t
−
arctan
w
h
)
2
v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2}
v=π24(arctanhgtwgt−arctanhw)2
从而,我们得到了CIoU对应的损失函数
L
C
I
o
U
=
1
−
I
o
U
+
ρ
2
(
b
,
b
g
t
)
c
2
+
α
v
\mathcal{L}_{C I o U}=1-I o U+\frac{\rho^{2}\left(\mathbf{b}, \mathbf{b}^{g t}\right)}{c^{2}}+\alpha v
LCIoU=1−IoU+c2ρ2(b,bgt)+αv
其中这个
α
\alpha
α参数,作者将其记作,但是没有说明原因,不过这和IoU损失相比,
α
<
1
\alpha<1
α<1保证了overlap area的 优先性
α
=
v
(
1
−
I
o
U
)
+
v
\alpha=\frac{v}{(1-I o U)+v}
α=(1−IoU)+vv
同时,作者手动将梯度计算出来了:同时说明使用该梯度计算时存在的一些问题:
∂
v
∂
w
=
8
π
2
(
arctan
w
g
t
h
g
t
−
arctan
w
h
)
×
h
w
2
+
h
2
∂
v
∂
h
=
−
8
π
2
(
arctan
w
g
t
h
g
t
−
arctan
w
h
)
×
w
w
2
+
h
2
\begin{aligned} \frac{\partial v}{\partial w} &=\frac{8}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) \times \frac{h}{w^{2}+h^{2}} \\ \frac{\partial v}{\partial h} &=-\frac{8}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) \times \frac{w}{w^{2}+h^{2}} \end{aligned}
∂w∂v∂h∂v=π28(arctanhgtwgt−arctanhw)×w2+h2h=−π28(arctanhgtwgt−arctanhw)×w2+h2w
使用上式计算梯度时存在的问题是:当 h , w h,w h,w的范围为 [ 0 , 1 ] [0,1] [0,1]时,非常容易产生梯度爆炸,因此作者将 1 w 2 + h 2 \frac{1}{w^{2}+h^{2}} w2+h21去掉,使用1来代替,得到了如下的表达式:
∂ v ∂ w = 8 π 2 ( arctan w g t h g t − arctan w h ) × h ∂ v ∂ h = − 8 π 2 ( arctan w g t h g t − arctan w h ) × w \begin{aligned} \frac{\partial v}{\partial w} &=\frac{8}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) \times {h} \\ \frac{\partial v}{\partial h} &=-\frac{8}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right) \times{w} \end{aligned} ∂w∂v∂h∂v=π28(arctanhgtwgt−arctanhw)×h=−π28(arctanhgtwgt−arctanhw)×w
在NMS中使用DIoU进行筛框
在筛框的时候,同时借助正则项IoU进行实现
s
i
=
{
s
i
,
I
o
U
−
R
D
I
o
U
(
M
,
B
i
)
<
ε
0
,
I
o
U
−
R
D
I
o
U
(
M
,
B
i
)
≥
ε
s_{i}=\left\{\begin{array}{l} s_{i}, I o U-\mathcal{R}_{D I o U}\left(\mathcal{M}, B_{i}\right)<\varepsilon \\ 0, \quad I o U-\mathcal{R}_{D I o U}\left(\mathcal{M}, B_{i}\right) \geq \varepsilon \end{array}\right.
si={si,IoU−RDIoU(M,Bi)<ε0,IoU−RDIoU(M,Bi)≥ε
在IoU中考虑两个中心点距离较远的box大致定义成不同的物体,不需要去掉。其中
s
i
s_i
si表示的是分类score,
ϵ
\epsilon
ϵ是NMS的阈值。仅仅几行代码,既可以将其集成到目标检测pipeline中。
(六)Experiments
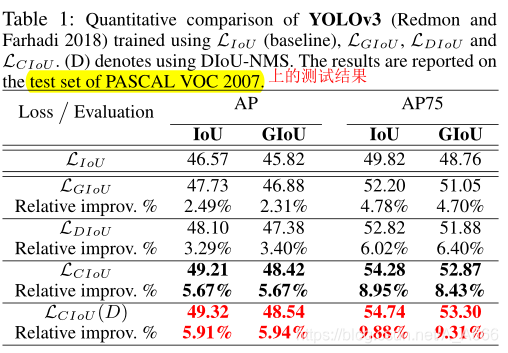
作者使用的数据集为PASCAL VOC以及MS COCO,使用的评估网络为One-stage(YOLO v3和SSD),以及two-stage(Faster R-CNN),
YOLOv3使用backbone为Darknet608,
接下来的实验中,仅仅报告在IoU度量下的结果
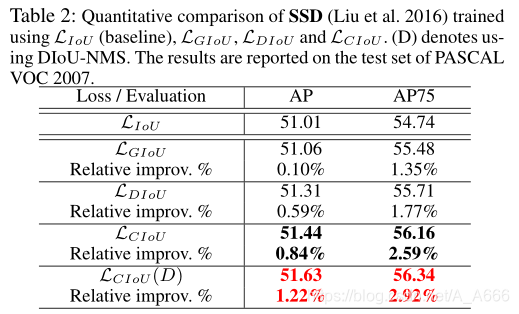
SSD,backbone使用 ResNet-50-FPN,默认的边界框回归损失使用的是SmoothL1 loss,作者这里将回归损失的权重设置为5
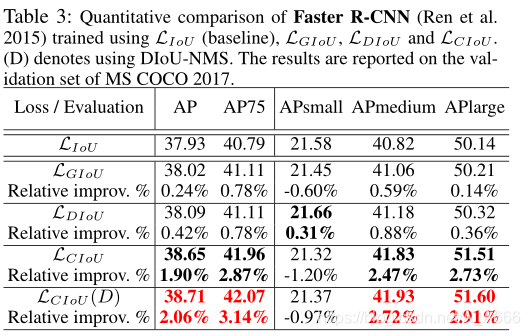
Faster R-CNN在COCO上的表现
- GIoU相比于IoU来说,仅仅具有较小的增益,
就AP small而言,CIoU Loss的性能比最初的IoU Loss稍差,而DIoU Loss比所有其他Loss都要好。也就是说长宽比的一致性可能对小物体的回归AP没有贡献。其实对于小物体来说,对于回归来说,中心点距离比长宽比更重要是合理的,长宽比可能会削弱两个盒子之间归一化距离的效果。
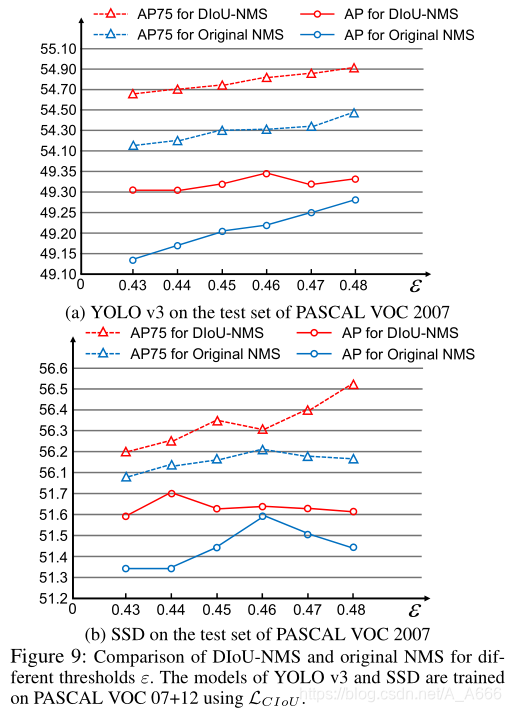
使用DIoU-NMS
在YOLOv3和SSD中,
ϵ
=
0.45
\epsilon = 0.45
ϵ=0.45,在Faster-RCNN中,
ϵ
=
0.5
\epsilon = 0.5
ϵ=0.5的
定性的分析结果
能够检测出更多的目标,
定量分析结果
使用CIoU Loss以及DIoU-NMS要比使用CIoU Loss以及普通的NMS取得更加好的表现结果。
(七)Conclusion
本文提出了bounding box回归的两种IoU Loss函数,即DIoU Loss和GIoU Loss,并提出了结合DIoU Loss中的正则性进行NMS的方法。通过直接最小化两个中心点的归一化距离,DIoU Loss可以实现比GIoU Loss更快的收敛。CIoU Loss考虑了三个几何属性,即重叠面积、中心点距离和纵横比,并导致更快的收敛和更好的性能。
(八)Notes
8.1 关于IoU Loss和Generalized IoU Loss的回顾
IoU
I
o
U
=
∣
B
∩
B
g
t
∣
∣
B
∪
B
g
t
∣
I o U=\frac{\left|B \cap B^{g t}\right|}{\left|B \cup B^{g t}\right|}
IoU=∣B∪Bgt∣∣B∩Bgt∣
其中,
B
g
t
=
(
x
g
t
,
y
g
t
,
w
g
t
,
h
g
t
)
B^{g t}=\left(x^{g t}, y^{g t}, w^{g t}, h^{g t}\right)
Bgt=(xgt,ygt,wgt,hgt)为Ground Truth box,
B
=
(
x
,
y
,
w
,
h
)
B=(x, y, w, h)
B=(x,y,w,h)为预测的box
LoU Loss
L
I
o
U
=
1
−
∣
B
∩
B
g
t
∣
∣
B
∪
B
g
t
∣
\mathcal{L}_{I o U}=1-\frac{\left|B \cap B^{g t}\right|}{\left|B \cup B^{g t}\right|}
LIoU=1−∣B∪Bgt∣∣B∩Bgt∣
GIoU Loss
L
G
I
o
U
=
1
−
I
o
U
+
∣
C
−
B
∪
B
g
t
∣
∣
C
∣
\mathcal{L}_{G I o U}=1-I o U+\frac{\left|C-B \cup B^{g t}\right|}{|C|}
LGIoU=1−IoU+∣C∣∣C−B∪Bgt∣
从公式上看,GIoU Loss相当于在IoU Loss的基础上增加了一个正则化项,在正则化项的作用下,即使预测box和Ground Truth box之间不存在overlap,预测box也会向着Ground Truth box移动。
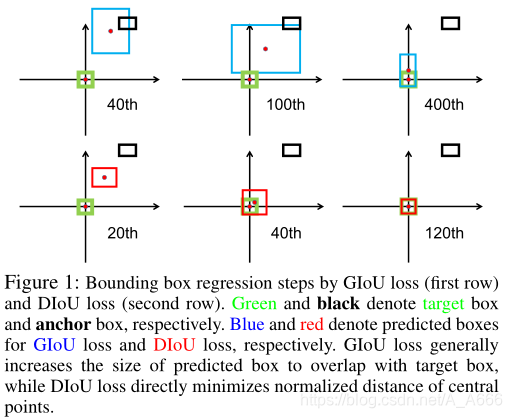
作者在本文中给出了GIoU Loss下降过程中bounding box的变化过程(感觉太强了,这个过程是怎么看出来的?):
作者指出仅仅从检测结果上是看不出来不同的IoU回归损失在回归bounding box上的作用,因此作者提出使用simulation experiments,从而能够更好地理解整个回归过程。
- 首先GIoU Loss期望去增大预测box的size,使得预测box和目标box 之间出现overlap,这里是通过正则项实现的
- 接着最大化bounding box之间的overlap面积
并且从上图中,我们可以看出DIoU在经过120K迭代后,能够和Ground Truth之间完全重合,收敛速度很快此外,GIoU在预测框被完全包含在真实框之中时,会退化到IoU上(没有明白作者提出这个问题是为了说明什么?)。
由于严重依赖IoU项进行收敛,GIoU需要进行more 迭代从而收敛,Usually GIoU loss cannot well converge in the state-of-the-art detection algorithms, yielding inaccurate detection.
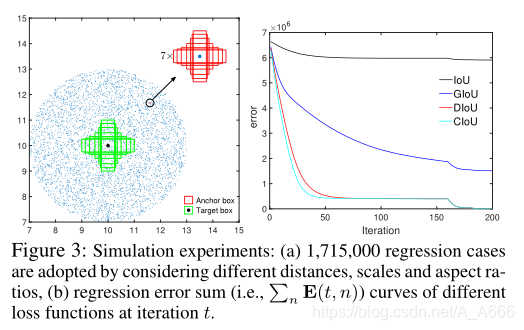
作者进行的仿真实验是什么呢?
作者在仿真实验中:
Gorund Truth boxes 的设置
面积为1,7种不同的长宽比(1:4, 1:3, 1:2, 1:1, 2::1, 3:1, 4:!),并且中心点位于(10,10)
anchor boxes的设置
在(10,10)为中心点,半径为3的范围内,均匀地撒下5000个点,每一个点对应着77个anchor boxes(7种尺度(面积分别为0.5, 0.67, 0.75, 1, 1.33, 1.5 and 2.),7种长宽比(1:4, 1:3, 1:2, 1:1, 2:1,3:1 and 4:1)),也就是一共50007*7个anchor boxes
令所有的anchor boxes 利用IoU Loss,以及梯度下降回归到7个Ground Truth boxes上,一共对应着500077*7种回归过程
上图中右侧纵轴error表示的是,所有回归情况(
5000
∗
7
∗
7
∗
7
5000*7*7*7
5000∗7∗7∗7)的损失之和(此处的性能是通过L1-norm来进行evaluated),而box参数的更新则是通过梯度下降进行的。并且从右图中我们可以看出:
- IoU Loss仅仅对那些目标框重叠的情况起作用,没有重叠的部分,无法使得参数值进行更新
- GIoU实际上增加了bounding box的大小,以与target box重叠,然后IoU项将使预测bounding box与目标box匹配,产生非常慢的收敛。
B i t = B i t − 1 + η ( 2 − I o U i t − 1 ) ∇ B i t − 1 B_{i}^{t}=B_{i}^{t-1}+\eta\left(2-I o U_{i}^{t-1}\right) \nabla B_{i}^{t-1} Bit=Bit−1+η(2−IoUit−1)∇Bit−1
其中 B i t B_{i}^{t} Bit是在t步的预测box, ∇ B i t − 1 \nabla B_{i}^{t-1} ∇Bit−1表示 B i B_i Bi在第t-1步迭代的损失的梯度值, η \eta η是更新的step。
这里的疑问是不应该沿着负梯度方向进行参数更新吗?
这里博主认为不沿着负梯度方向进行更新的原因在于这里的目标是IoU/GIoU/DIoU/CIoU,而不是对应的损失函数值
同时这里乘上 η ( 2 − I o U i t − 1 ) \eta\left(2-I o U_{i}^{t-1}\right) η(2−IoUit−1)的目的在于加速收敛过程。
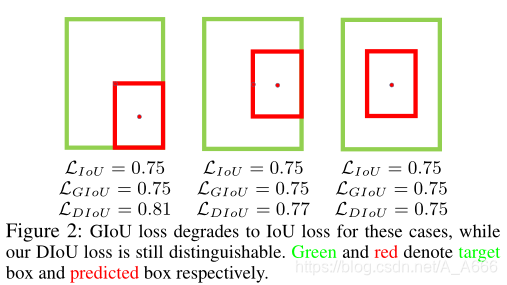
8.2 DIoU Loss和GIoU Loss的区别
- DIoU 对于回归问题的scale依然是不变的
- 当non-overlapping情况下,DIoU Loss可以提供一个移动方向使得可以进行bounding box的回归
- 当两个bounding boxes能够很好地匹配时, L I o U = L G I o U = L D I o U = 0 \mathcal{L}_{I o U} = \mathcal{L}_{G I o U}=\mathcal{L}_{D I o U}=0 LIoU=LGIoU=LDIoU=0,当两个boxes距离很远时, L G I o U = L D I o U → 2 \mathcal{L}_{G I o U}=\mathcal{L}_{D I o U} \rightarrow 2 LGIoU=LDIoU→2
DIoU相比于GIoU存在的几个优点:
- DIoU Loss可以直接最小化两个box的距离,因此收敛速度比GIoU Loss快得多
- 当两个box存在着遮挡时,(博主觉得这里作者说的问题是目标box将预测box包含在内的情况),此时DIoU的正则化项仍然可以起作用,但是GIoU的正则化项却没有办法继续起作用下去。
(九)Sentences
- Despite of these different detection frameworks, bounding box regression is the crucial step to predict a rectangular box to locate the target object.(尽管存在着不同的检测框架,bounding box回归是用矩形框来定位目标的关键步骤)
- In this section, we briefly survey relevant works including object detection methods, loss function for bounding box regression and non-maximum suppression(Related work 相关工作的开头部分)