十二、树结构的实际应用—赫夫曼树

1、赫夫曼树

1.1 基本介绍

给定 n 个权值作为 n 个叶子节点，构造一棵二叉树，若该树的带权路径长度（wpl）达到最小，称这样的二叉树为最优二叉树，也称哈夫曼树（Huffman Tree），有的翻译为霍夫曼树、赫夫曼树
赫夫曼树是带权路径长度最短的树，权值较大的节点离根节点较近

1.2 重要概念

路径和路径长度：在一棵树中，从一个节点往下可以达到的孩子或者孙子节点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根节点的层数为1，则从根节点到第 L 层节点的路径长度为 L-1
节点的权及带权路径长度：若将树中节点赋给一个有着某种含义的数值，则这个数值称为该节点的权。节点的带权路径长度为：从根节点到该节点之间的路径长度与该节点的权的乘积
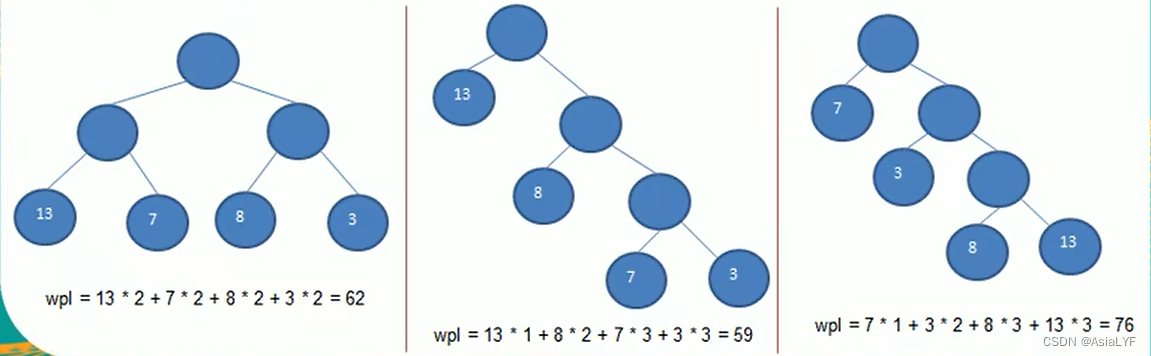
树的带权路径长度：树的带权路径长度规定为所有叶子节点的带权路径长度之和，记为 WPL（Weighted Path Length）。权值越大的节点离根节点越近的二叉树才是最优二叉树

下面是一些 WPL 计算的例子：（长度为59的是最优二叉树）
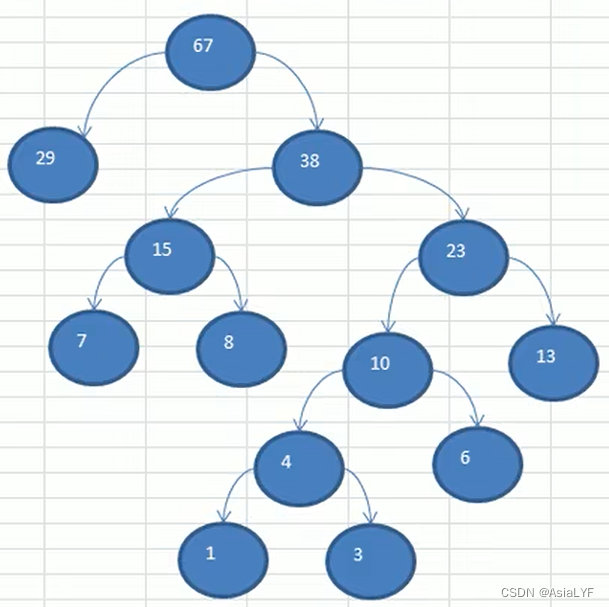
在这里插入图片描述

1.3 赫夫曼树构建思路图解

要求：给你一个数列 {13, 7, 8, 29, 6, 1} ，要求转化为一颗赫夫曼树

构成赫夫曼树的步骤：

将数列从小到大进行排序，每个数据都是一个节点，每个节点可以看成是一棵最简单的二叉树
取出根节点权值最小的两棵二叉树
组成一棵新的二叉树，该新的二叉树的根节点的权值是前面两棵二叉树根节点的权值和
再将这棵新的二叉树。以根节点的权值大小，再次排序，不断重复这四个步骤（上面三个+当前一个），直到数列中所有的数据都被处理，就得到了一颗赫夫曼树

下面是示意图：
在这里插入图片描述

1.4 赫夫曼树代码实现

public class HuffmanTreeDemo {

	public static void main(String[] args) {
		 int arr[]=new int[]{13,7,8,3,29,6,1};
		 Node root = createHuffmanTree(arr);
		 preSort(root);
	}
	
	public static void preSort(Node root) {
		if (root != null) {
			root.preSort();
		}else {
			 System.out.println("该赫夫曼树是空树");
		}
	}
	
	public static Node createHuffmanTree(int[] arr) {
		//第一步：为了操作方便：
		/**
		 * 1、遍历arr数组
		 * 2、将arr的每个元素构建成一个Node
		 * 3、将Node放到ArrayList中
		 */
		List<Node> nodes = new ArrayList<Node>();
		for (int value : arr) {
			nodes.add(new Node(value));
		}
		
		while (nodes.size() > 1) {//这个主要是因为nodes一直在remove，到最后就剩一个节点。
			Collections.sort(nodes);
			
			//取出根节点权值最小的两个二叉树
            //（1）取出权值最小的节点（二叉树），一个节点也可以看作是一个最简单的二叉树
			Node leftNode = nodes.get(0);
			 //（2）取出权值第二小的节点（二叉树）
			Node rightNode = nodes.get(1);
			 //（3）构建一个新的二叉树
			Node parent = new Node(leftNode.value + rightNode.value);//左右节点权值的加和才是父节点
			parent.left = leftNode;
			parent.right = rightNode;
			 //（4）从ArrayList中删除处理过的二叉树
			nodes.remove(leftNode);
			nodes.remove(rightNode);
			//(5)将parent加入nodes
			nodes.add(parent);
		}
		
		  //返回哈夫曼树的root节点，其实最后也就剩一个节点了
        return nodes.get(0);

	}

}

class Node implements Comparable<Node>{
	
	int value; //节点权值
	Node left; //指向左子节点
	Node right; //指向右子节点
	
	public Node(int value) {
		this.value = value;
	}
	
	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}

	public void preSort() {
		System.out.println(this);
		if (this.left != null) {
			this.left.preSort();
		}
		if (this.right != null) {
			this.right.preSort();
		}
	}

	@Override
	public int compareTo(Node o) {
		// 从小到大排序
		return this.value - o.value;
	}
	
}

2、赫夫曼编码

2.1 基本介绍

赫夫曼编码也翻译为哈夫曼编码（Huffman Coding），又称霍夫曼编码，是一种编码方式，属于一种程序算法
赫夫曼编码是哈夫曼树在电讯通信中的经典的应用之一
赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%~90%之间
赫夫曼编码是可变字长编码（VLC）地一种，Huffman 于 1952 年提出一种编码方法，称之为最佳编码

2.2 原理剖析

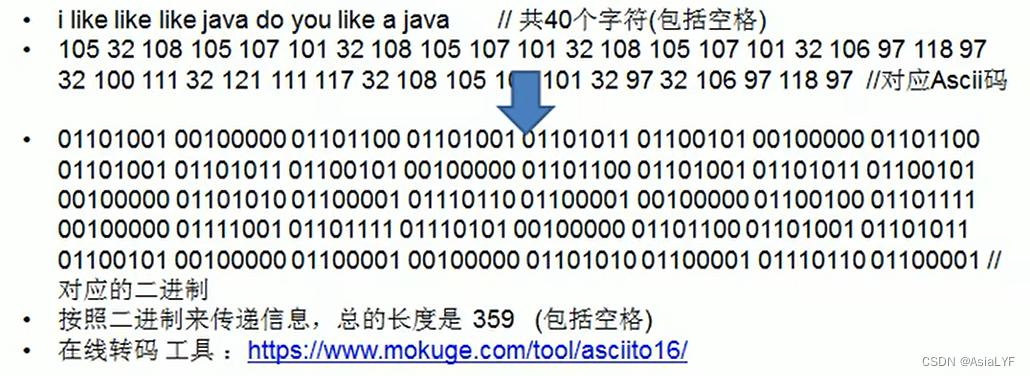
通信领域中信息地处理方式1：定长编码
[参考ASCII码表]
在这里插入图片描述
通信领域中信息地处理方式2：变长编码

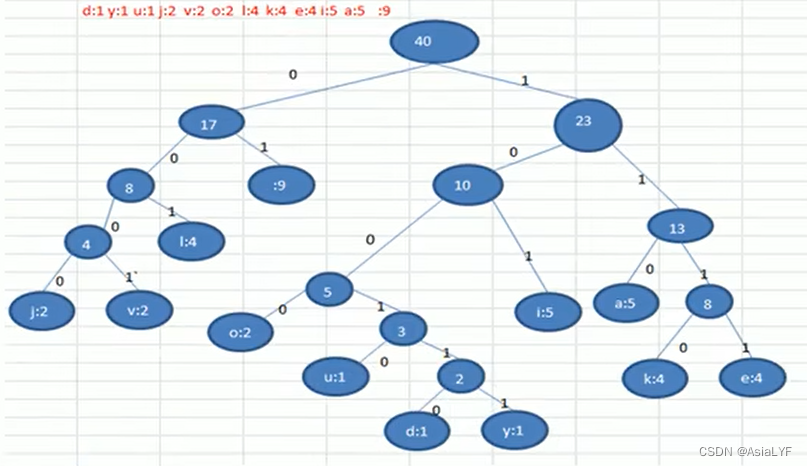
通信领域中信息地处理方式3：赫夫曼编码

最后得到的赫夫曼树为：

此编码需满足前缀编码，即字符的编码都不能是其他字符编码的前缀。不然会造成匹配的多义性，赫夫曼编码是无损处理方案。
注意，这个赫夫曼树根据排序方法不同，也可能不太一样，这样对应赫夫曼编码也不完全一样，但是 WPL 是一样的，都是最小的，最后生成的赫夫曼编码的长度是一样的，

2.3 最佳实践：数据压缩和解压

1) 数据压缩

在这里插入图片描述

2）数据解压