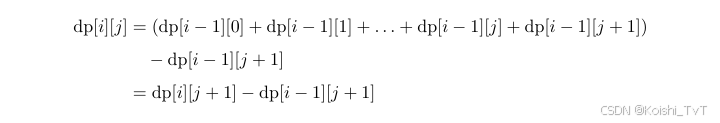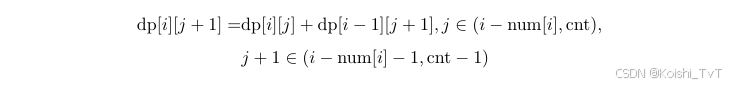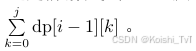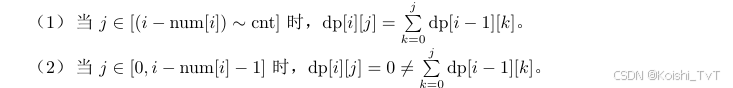别忘了请点个赞+收藏+关注支持一下博主喵!!!! ! ! ! !
关注博主,更多蓝桥杯nice题目静待更新:)
动态规划
三、括号序列
【问题描述】
给定一个括号序列,要求尽可能少地添加若干括号使得括号序列变得合法,当添加 完成后,会产生不同的添加结果,请问有多少种本质不同的添加结果。
两个结果是本质不同的是指存在某个位置一个结果是左括号,而另一个是右括号。
例如,对于括号序列 (((),只需要添加两个括号就能让其合法,有以下几种不同的添加结果:()()() 、()(()) 、(())()、(()()) 和 ((()))。
【输入格式】
输入一行包含一个字符串s,表示给定的括号序列,序列中只有左括号和右括号。
【输出格式】
输出一个整数表示答案,答案可能很大,请输出答案除以1000000007(即109+7) 的余数。
【样例输入】
((()
【样例输出】
5
【评测用例规模与规定】
对于40%的评测用例,|s|⩽200。
对于所有评测用例,1⩽|s|⩽5000。
解析:
在开始解题之前,我们先分析两个问题。
问题1. 什么情况下必须要添加左括号,什么情况下必须添加右括号?
问题2. 我们添加的左括号会和我们添加的右括号匹配吗?
对于问题1,我们可从以下两方面作进一步思考:
(1)当一个右括号之前已经没有可以与其相匹配的左括号时,我们必须要添加左括号。例如() ),从左往右看,第二个右括号之前已经没有左括号可以与其匹配(第一个左括号和第一个右括号匹配),这时候我们就必须添加左括号。
(2)当一个左括号之后已经没有可以与其相匹配的右括号时,我们必须要添加右括号。例 如(( ),从右往左看,第二个左括号之后已经没有右括号可以与其匹配(第一个右括号和第 一个左括号匹配),这时候我们就必须添加右括号。
对于问题2,答案是“不会”。
我们可以使用反证法来证明:
(1)假设操作完成后的括号序列为 XXX ( XXX ) XXX ,(、) 为我们添加的互相匹配 的左括号和右括号,X 表示原序列的括号,或是我们添加的与原序列括号相匹配的 括号。
(2)那么该序列 XXX(XXX)XXX 若是一个合法序列,则将 (、) 去掉后的序列 XXX XXX XXX也会是个合法序列(对于一个合法的括号序列,去掉任意一对匹配的左右括号,它也依旧合法)。
(3)所以如果我们添加的左右括号相互匹配,它们将起不到什么作用,只会徒然增长序 列的长度。而题目要求我们的序列长度尽可能短,所以我们添加的左括号不会和我 们添加的右括号匹配( 即我们添加的左括号只会受原序列中的括号影响,添加的右括号只会受原序列中的括号影响)。
因此,我们可以将左括号的添加方案和右括号的添加方案分开计算,然后再将其合并为 答案(因为左括号和右括号的添加是互不影响的、独立的,所以 答案 = 左括号的添加方案数 × 右括号的添加方案数)。
下面分别给出3种解题方式,分别是暴力做法、能拿 40% 分数的做法、满分做法。大家仔细体验这3种解题方式的特点,其中 “ 能拿 40% 分数的做法 ” 给出的解题方式,虽然拿不了满分, 但在实际竞赛中,也可以视情况使用。
方式1:暴力做法
本题作为2021年蓝桥杯省赛压轴题之一,相信绝大部分人在做的时候都会一头雾水,甚 至在已知上面信息的情况下,也还是会找不到切入点。
不过没有关系,蓝桥杯毕竟是个根据通过的数据量来给分的比赛,所以我们并不需要在 第一步就思考出它的满分做法。
那第一步该做什么呢?暴力!
有一个做题技巧:在面对一道完全没有头绪的题目时,请不要傻等着浪费时间,可以先尝试用暴力的方法解题,然后再在暴力的基础上思考如何优化复杂度。这样不仅能帮助梳理 题目的约束,同时也可以发现题目的隐含性质。
前面我们分析出添加的左右括号是互不影响的,所以接下来让我们先来尝试下如何用暴 力求解的左括号的添加方案数。
首先确定一种暴力方法,比如在每个右括号前添加若干个左括号从而产生若干个新的括号序列,再从中计算最短的合法括号序列的个数。
假设原序列中有 cnt 个右括号,以这 cnt 个右括号为分界线,一共可以划分出 cnt+1 个区域:区域 1 )区域 2 ) 区域 3 )... ) 区域 cnt+1。显然我们只能在第1∼cnt个区域添加左 括号,因为若是在第cnt+1区域添加左括号,将不会有右括号可以与它匹配。
那每个区域要添加多少个左括号呢?加多少个左括号都可以。因此我们可以枚举每个区域要添加的括号数。
不过既然要枚举,就得设置一个枚举上限。很显然,我们添加的左括号数不可能大于原序列中的右括号数,所以可以设置每个区域的上限为原序列中的右括号数cnt。
设置完上限后,我们就可以从第一个区域开始依次枚举要添加的左括号数。
当第 cnt 个区域枚举结束后,将会得到一个全新的括号序列。根据枚举的不同,我们也将得到多个全新的、不同的括号序列。我们再从这些新的括号序列中计算长度最短的、合法 的序列个数,即可得到答案。
可问题又来了,如何判断一个括号序列是否合法呢?
这个简单。我们添加左括号的目的是为了让原序列中的每个右括号之前都有对应的左括号与其相匹配,所以只要新的括号序列中的每个右括号之前有对应的左括号可以与其相匹配 即为合法序列。
上述整个过程可以使用DFS来实现。
参考代码如下【时间复杂度为 O(len×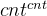
#include <bits/stdc++.h>
using namespace std;
int n, cnt, ans, min_len = 0x3f3f3f3f;
string s;
bool check(string s) {
int left = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') left++;
else left--;
if (left < 0) return false;
}
return true;
}
void dfs(int p, string new_s) {
if (p == n) { // 枚举结束
if (check(new_s)) { // 判断这个新的括号序列是否合法
if (new_s.size() == min_len) ans++; // 如果长度和最小长度相同,则答案个数+1
else if (new_s.size() < min_len) {
min_len = new_s.size();
ans = 1; // 如果长度比最小长度还短,则作为新的最小长度
}
}
return;
}
if (s[p] == '(')
dfs(p + 1, new_s + '(');
else {
for (int i = 0; i <= cnt; i++) { // 如果是右括号, 则在该右括号前枚举要添加的左括号个数i
string add = "";
for (int j = 1; j <= i; j++) add += '(';
dfs(p + 1, new_s + add + ')');
}
}
}
signed main() {
cin >> s;
n = s.size();
for (int i = 0; i < s.size(); i++)
if (s[i] == ')') cnt++;
dfs(0, "");
cout << ans << '\n';
return 0;
}以上的暴力做法对于第1∼cnt个区域都从0∼cnt枚举了要添加的左括号个数,这无 疑产生了大量不合法的括号序列,那要如何减少不合法的括号数呢?可以从每个区域的枚举上限入手。
我们令每个区域的枚举上限都为cnt的理由是“添加的左括号数不可能大于原序列中的右括号数”。这里添加的左括号数指的是所有区域的总添加数,而不是单一区域的添加数。
因此,我们可以设置一个动态的枚举上限total来简单优化一下枚举的次数(详见下方代码)。
参考代码如下
void dfs(int p, string new_s, int total) { // total表示还可以添加的左括号数。在开始DFS之前,total = cnt
if (p == n) { // 枚举结束
if (check(new_s)) { // 判断这个新的括号序列是否合法
if (new_s.size() == min_len)
ans++; // 如果长度和最小长度相同,则答案个数+1
else if (new_s.size() < min_len) {
min_len = new_s.size();
ans = 1; // 如果长度比最小长度还短,则作为新的最小长度
}
}
return;
}
if (s[p] == '(')
dfs(p + 1, new_s + '(', total);
else {
for (int i = 0; i <= total; i++) { // 如果是右括号, 则在该右括号前枚举要添加的左括号个数i
string add = "";
for (int j = 1; j <= i; j++)
add += '(';
dfs(p + 1, new_s + add + ')', total - i); // 当前区域添加了i个左括号,那后面的区域可以添加的左括号总数为total-i
}
}
}与优化前相比,虽然上述方法能一定程度上减少一些不合法的括号序列,但产生的不合法括号序列依旧很多,这并不能起到很有效的作用。
那还能进行哪些优化呢?我们重新思考这句话:添加的左括号数不可能大于原序列中的右括号数。既然如此,那到底要添加多少左括号呢?
回顾一下,我们添加左括号的目的是让原序列中的每个右括号的前面都有对应的左括号 与其相匹配。也就是说,只有在原序列中的某个右括号之前没有可以与其相匹配的左括号时, 我们才有必要添加左括号。
例如,对于括号序列 ) ( ( ) ) ) ,它的第1个右括号前没有可以与其相匹配的左括号,所 以我们至少要添加1个左括号;第2∼3个右括号前都有左括号可以与其相匹配,所以至少 要添加的左括号个数为0;第4个右括号前没有可以与其相匹配的左括号,所以我们至少要添加1个左括号。
有了这个条件,我们就可以制定贪心策略:只有当必须要添加左括号时才添加左括号,这样就可以保证我们添加的括号总数最小(记添加的最小总数为need),相关代码参考完整代 码的第26∼31行。
这样我们就可以将枚举上限设置为need(need⩽cnt),从而减少不合法括号序列的 产生。不过很显然这优化力度还远远不够,甚至在最坏的情况下(need=cnt)起不到任何作用。
那还有什么办法可以优化呢?能不能一次性避免所有不合法括号序列的产生呢?
答案自然是“能”。只要保证产生的括号序列都是合法的即可避免不合法括号序列的产生。
那如何保证产生的括号序列都是合法的呢?只要保证每个右括号之前都有可以与之匹配的左括号即可。
于是我们就可以在DFS过程中记录未匹配的左括号个数,当某个右括号之前未匹配的 左括号个数为0时,我们就必须添加左括号(从1开始枚举添加的左括号个数)。这样就能保证产生的括号序列都是合法的,也就不需要用 check() 函数来判断序列的合法性。完整代码如下。
参考代码如下
#include <bits/stdc++.h>
using namespace std;
int n, cnt, ans, min_len = 0x3f3f3f3f;
string s;
void dfs(int p, string new_s, int total, int left) {
if (p == n) { // 枚举结束
if (new_s.size() == min_len)
ans++; // 如果长度和最小长度相同,则答案个数+1
else if (new_s.size() < min_len) {
min_len = new_s.size();
ans = 1; // 如果长度比最小长度还短,则作为新的最小长度
}
return;
}
if (s[p] == '(')
dfs(p + 1, new_s + '(', total, left + 1); // 未匹配的左括号个数+1
else {
int st = 0; // 枚举起点
if (left == 0) st = 1; // 该右括号之前未匹配的左括号个数为0,那么为了保证序列合法,它之前至少要添加一个左括号
for (int i = st; i <= total; i++) { // 如果是右括号,则在该右括号前枚举要添加的左括号个数i,从st开始枚举
string add = "";
for (int j = 1; j <= i; j++)
add += '(';
dfs(p + 1, new_s + add + ')', total - i, left + i - 1); // 需要从未匹配的左括号中拿出一个和当前右括号匹配,所以要-1
}
}
}
signed main() {
cin >> s;
n = s.size();
for (int i = 0; i < s.size(); i++)
if (s[i] == ')')
cnt++;
int need = 0, left = 0; // need表示最少需要添加的左括号数,left表示未匹配的左括号个数
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(')
left++; // 未匹配的左括号个数+1
else
left--; // 拿走一个左括号与该右括号匹配,左括号个数-1
if (left < 0)
need++, left = 0; // 该右括号之前没有左括号可以与其匹配,此时就必须添加左括号
}
dfs(0, "", need, 0);
cout << ans << '\n';
return 0;
}以上就是暴力求解左括号添加方案数的过程,右括号添加方案数的求解类似,就不过多阐述。
暴力的优化到此结束。
可见,采用暴力解法虽然可以避免所有不合法括号序列的产生,但产生出的合法括号序列的数量也相当多,因此我们无法通过“暴力”来解决本题。
方式2:能拿40%分数的做法
1. 求原括号序列中第 i (1 ⩽ i ⩽cnt ) 个右括号之前的左括号数
我们虽然求解了need(最少需要添加的左括号数),但这个 need 是对于整个括号序列的。而对于原括号序列的某个右括号,我们并不知道它之前必须要添加多少个左括号。
于是我们可以定义原括号序列中第i个右括号之前的左括号数为num[i],那么第 i 个右括号之前需要添加的左括号数就等于i−num[i]。
num[i] 的求解如下。
参考代码如下:
int left = 0, cnt = 0;
for (int i = 1; i <= n; i++) {
if (s[i] == ')') {
num[++cnt] = left;
}
if (s[i] == '(') {
left++; // left 表示原序列区间[1, i]的左括号个数
}
}2. 计算方案数
通过前面的步骤,我们将问题转换成了 “ 往cnt个区域中添加need个左括号的合法方案数 ” 的求解。
假设现在有i个区域(右括号),一共往这个i个区域中添加了j个左括号,要想得出其中的合法方案数,该怎么计算呢?
我们可以先定义 dp[i][j] 来表示往前 i 个区域中共添加了 j 个左括号后的所有合法方案数,而往前i个区域中添加了j个左括号相当于往前i−1个区域中添加了k(0 ⩽ k ⩽j )个 左括号,并往第i个区域中添加了 j−k 个左括号。由此,我们可以就可推出dp[i][j]的状态 转移式。
提示如下:
不过要想求解dp[i][j] ,只有状态转移式还不够,我们还需确定其初状态(即确定i=1 时dp[1][j] 对应的值)。
i =1 时的特殊情况我们可以分为以下两部分讨论。
(1)j ∈(1∼need)。显然,前 1 个区域(右括号)添加了1,2,3, ..., need 个左括号的 方案数都为1(need 表示最少需要添加的左括号个数),所以dp[1][1∼need]=1。
(2)j =0。这部分又可细分为两种情况。
• 第1个区域包含原序列的左括号,那么dp[1][0] = 1,即前 1 个区域(右括号) 添加了0个左括号的方案数为1。
• 第1个区域不包含原序列的左括号,那么j=0是不合法的,该情况不能作为一 个方案(对于一个合法序列的任意前缀,左括号的个数一定要大于等于右括号), 所以dp[1][0] = 0 。
【由于我们要的是合法序列,所以当右括号的个数为i时,它前面的左括号的个数必然大 于等于i,即添加的左括号数j +原序列的左括号数num[i]⩾i。】
接下来,我们就可以完成dp[i][j] 的求解。
参考代码如下
for (int i = 1; i <= need; i++)
dp[1][i] = 1;
if (num[1] > 0)
dp[1][0] = 1;
for (int i = 2; i <= cnt; i++) {
// 1. j + num[i] >= i
// 2. 最少添加的数量为need
for (int j = i - num[i]; j <= need; j++) {
for (int k = 0; k <= j; k++) {
dp[i][j] += dp[i-1][k];
dp[i][j] %= mod;
}
}
}【答案可用dp[cnt][need]表示,即前cnt个区域添加了need个左括号的所有合法方案数。】
至此,添加左括号的方案数就计算完成了。
对于右括号的添加方案,我们可以将原括号序列反转,并令(为)、)为(,然后按照求左 括号的方案数的方法再求一遍即可。
参考代码如下【时间复杂度为O(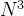
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e3 + 10, mod = 1e9 + 7;
string s;
int dp[N][N], num[N];
int calc(int need, bool flag) {
memset(dp, 0, sizeof(dp));
memset(num, 0, sizeof(num));
// flag=1表示统计添加左括号的方案数; flag=0表示统计添加右括号的方案数(翻转)
if (!flag) {
reverse(s.begin(), s.end());
for (int i = 0; i < s.size(); i++) {
if (s[i] == ')') s[i] = '(';
else s[i] = ')';
}
}
int left = 0, cnt = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] == ')') num[++cnt] = left; // cnt为右括号的编号
if (s[i] == '(') left++; // left表示原序列区间[1, i]的左括号的个数
}
// 区域1有左括号时dp[1][0] = 1, 否则dp[1][0] = 0
if (num[1] > 0) dp[1][0] = 1;
for (int i = 1; i <= cnt; i++) dp[1][i] = 1;
for (int i = 2; i <= cnt; i++) {
// 1. j + num[i] >= i
// 2. 最少添加的数量为need
for (int j = max(0LL, i - num[i]); j <= need; j++) {
for (int k = 0; k <= j; k++) {
dp[i][j] += dp[i-1][k];
dp[i][j] %= mod;
}
}
}
return dp[cnt][need];
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> s;
int need = 0, tmp = 0; // need表示最少需要添加的左括号数,tmp表示序列前缀和
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') tmp++;
else tmp--;
if (tmp < 0) need++, tmp++; // tmp < 0表示右括号数大于左括号数,此时需要添加左括号使得左括号数>=右括号数
}
int need2 = tmp;
cout << calc(need, 1) * calc(need2, 0) % mod << '\n';
return 0;
}方式3:满分做法
要想拿满分需要在 “ 方式2:能拿40%分数做法 ” 的步骤上作进一步优化。
在上述步骤中,我们得到dp[i][j]=dp[i−1][0]+dp[i−1][1]+...+dp[i−1][j]。
如果接触过“完全背包”,那就应该联想到用完全背包的前缀和来优化:
已知:::::
移项得:::
再令 j = j − 1,得:::
这样就可以去掉一层循环,复杂度为O(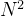
而我们在求解dp[i][j] 时,有以下两种情况。
所以dp[i][j] = dp[i−1][j] +dp[i][j − 1] 的转移并不完全合法。
那怎么办呢?
我们可以用类似的方法来优化。 定义pre[] 数组。
这样时间复杂度就优化到了O(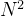
参考代码6-3-7 【时间复杂度为 O(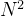
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e3 + 10, mod = 1e9 + 7;
string s;
int dp[N][N], num[N], pre[N], nex[N];
// 计算方案数
int calc(int need, bool flag) {
if (!need) return 1; // 不需要添加括号也是一种方案
memset(dp, 0, sizeof(dp));
memset(num, 0, sizeof(num));
memset(pre, 0, sizeof(pre));
memset(nex, 0, sizeof(nex));
// flag = 1 表示统计添加左括号的方案数; flag = 0 表示统计添加右括号的方案数(翻转)
if (!flag) {
reverse(s.begin(), s.end());
for (int i = 0; i < s.size(); i++) {
if (s[i] == ')') s[i] = '(';
else s[i] = ')';
}
}
int left = 0, cnt = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] == ')') num[++cnt] = left; // cnt为右括号的编号
if (s[i] == '(') left++; // left表示原序列区间[1, i]的左括号的个数
}
// 区域1有左括号时dp[1][0] = 1, 否则dp[1][0] = 0
if (num[1] > 0) dp[1][0] = 1, pre[0] = 1;
for (int i = 1; i <= cnt; i++) dp[1][i] = 1, pre[i] = pre[i - 1] + 1;
for (int i = 2; i <= cnt; i++) {
for (int j = 0; j <= need; j++) nex[j] = 0;
for (int j = max(0LL, i - num[i]); j <= need; j++) {
dp[i][j] = pre[j];
if (j - 1 < 0) nex[j] = dp[i][j];
else nex[j] = (nex[j - 1] + dp[i][j]) % mod;
}
for (int j = 0; j <= need; j++) pre[j] = nex[j]; // 先用nex[]存储dp[i-1]的信息,再将nex[]的值赋给pre[],这样下次循环pre[]存的值就是dp[i-1]的值
}
return dp[cnt][need];
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> s;
int need = 0, pre = 0; // need表示最少需要添加的左括号数,pre表示序列前缀和
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') pre++;
else pre--;
if (pre < 0) need++, pre++; // pre < 0表示右括号数大于左括号数,此时需要添加左括号使得左括号数>=右括号数
}
int need2 = pre;
cout << calc(need, 1) * calc(need2, 0) % mod << '\n';
return 0;
}四、异或三角
【问题描述】
给定T个数n1,n2,...,nT,对每个ni请求出有多少组a,b,c满足:
(1)1⩽a,b,c⩽ni;
(2)a⊕b⊕c=0,其中⊕表示二进制按位异或;
(3)长度为a,b,c的三条边能组成一个三角形。
【输入格式】
输入的第一行包含一个整数T。
接下来T行每行一个整数,分别表示n1,n2,...,nT。
【输出格式】
输出T行,每行包含一个整数,表示对应的答案。
【样例输入】
【样例输出】
【评测用例规模与规定】
对于10%的评测用例,T=1,1⩽ni⩽200;
对于20%的评测用例,T=1,1⩽ni⩽2000;
对于50%的评测用例,T=1,1⩽ni⩽220;
对于60%的评测用例,1⩽T⩽100000,1⩽ni⩽220;
对于所有评测用例,1⩽T⩽100000,1⩽ni⩽230。
解析:
题目对于我们要求解的a,b,c 设定了两个十分重要的限制条件。
• 限制条件1: a ⊕ b ⊕ c=0。
• 限制条件2: 长度为a,b,c 的三条边能组成一个三角形。
这两个条件不难解读。
根据异或运算的归零律(相同数的异或值为0)可得
• (a⊕b)=c。
• (b⊕c) =a。
• (a⊕c)=b。
根据三角形的不等式定理(两边之和大于第三边)可得
• a+b>c。
• a+c>b。
• b+c>a。
解读完两个限制条件后,我们进入解题环节。
(这里我们不再赘述,直接给100%满分做法)
对于50%、60%分数做法的测试数据,因为a的最大范围为220=1048576,所以我们 可以通过枚举来确定a。但在满分做法的测试数据中,n的最大范围为230次方,显然,枚举是不可能的了。
那怎么办呢?
回顾一下我们先前对于各个得分点的处理步骤。
(1)10%分数:暴力枚举3个数并统计答案。
(2)20%分数:无法枚举3个数,转换成枚举两个数,通过两个数的异或计算得到第三 个数并统计答案。
(3)50%分数、60%分数:无法枚举两个数,转换成枚举一个数、数位dp一个数,通过两个数的异或计算得到第三个数并统计答案。
既然此前我们在无法枚举一个数时,使用数位dp来代替处理,那么现在无法枚举a时, 是不是也能用数位dp来代替处理呢?
下面来尝试一下。
还是以a为最大值,先对其进行处理。对于a,由于它是第一个要确定的数,因此我们仅须对它增设一个限制条件:a < n (将其上界定为n即可)
接下来考虑b(此时a已确定)
参考代码如下【时间复杂度为O(T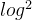
#pragma GCC target("avx2,fma")
#pragma GCC optimize("O3")
#pragma GCC optimize("unroll-loops")
#include <bits/stdc++.h>
#define int long long
using namespace std;
// 快速读取整数
template<typename T>
void read(T &res) {
bool flag = false;
char ch;
while (!isdigit(ch = getchar())) (ch == '-') && (flag = true);
for (res = ch - 48; isdigit(ch = getchar()); res = (res << 1) + (res << 3) + ch - 48);
flag && (res = -res);
}
// 快速输出整数
template<typename T>
void Out(T x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) Out(x / 10);
putchar(x % 10 + '0');
}
int n, dp[32][2][2][2][2], num[32];
// 深度优先搜索
inline int dfs(int len, bool limit1, bool limit2, bool ok1, bool ok2) {
if (!len) return ok2 ? 1 : 0;
if (~dp[len][limit1][limit2][ok1][ok2]) return dp[len][limit1][limit2][ok1][ok2];
int up1 = limit1 ? num[len] : 1, res = 0;
for (int i = 0; i <= up1; i++) {
int up2 = limit2 ? i : 1;
for (int j = 0; j <= up2; j++) {
if (!ok1 && !i && j) continue;
res += dfs(len - 1, limit1 && i == up1, limit2 && j == up2, ok1 || (j == i && j == 1), ok2 || (j == 1 && j != i));
}
}
return dp[len][limit1][limit2][ok1][ok2] = res;
}
// 解决问题
inline int solve(int n) {
memset(dp, -1, sizeof(dp));
int len = 0;
while (n) {
num[++len] = n & 1;
n >>= 1;
}
return dfs(len, 1, 1, 0, 0);
}
signed main() {
int T = 1;
read(T);
while (T--) {
read(n);
Out(solve(n) * 3), putchar('\n');
}
return 0;
}别忘了请点个赞+收藏+关注支持一下博主喵!!!! ! ! !
关注博主,更多蓝桥杯nice题目静待更新:)