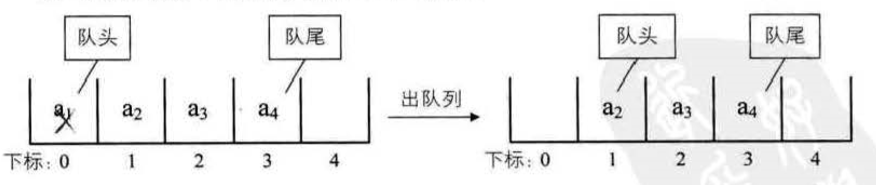
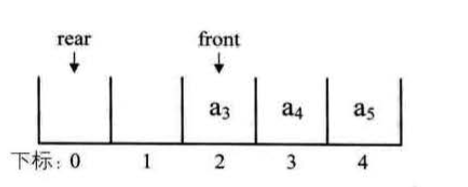
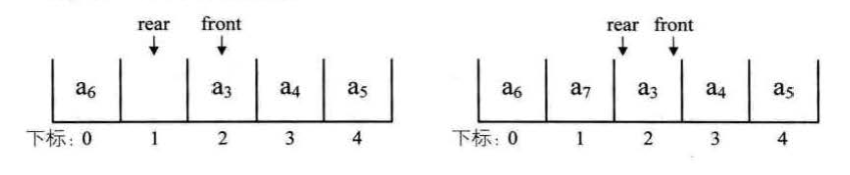
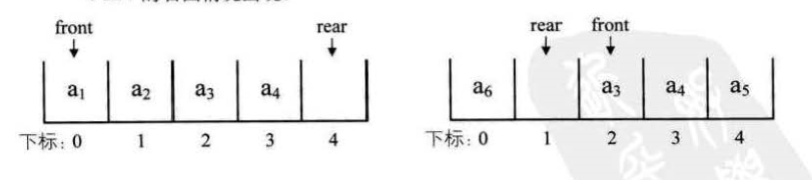
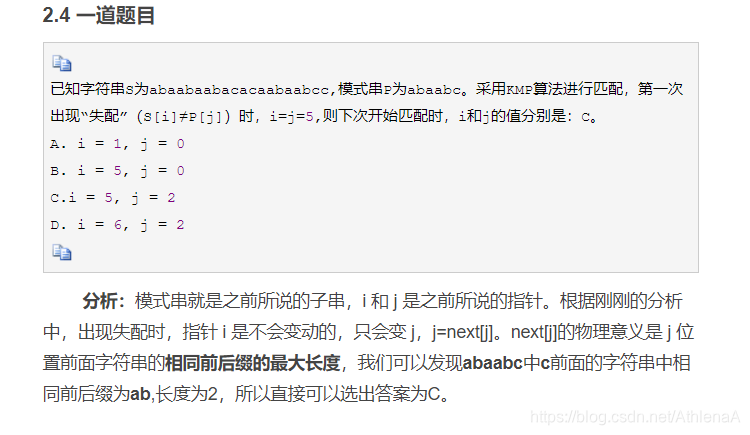
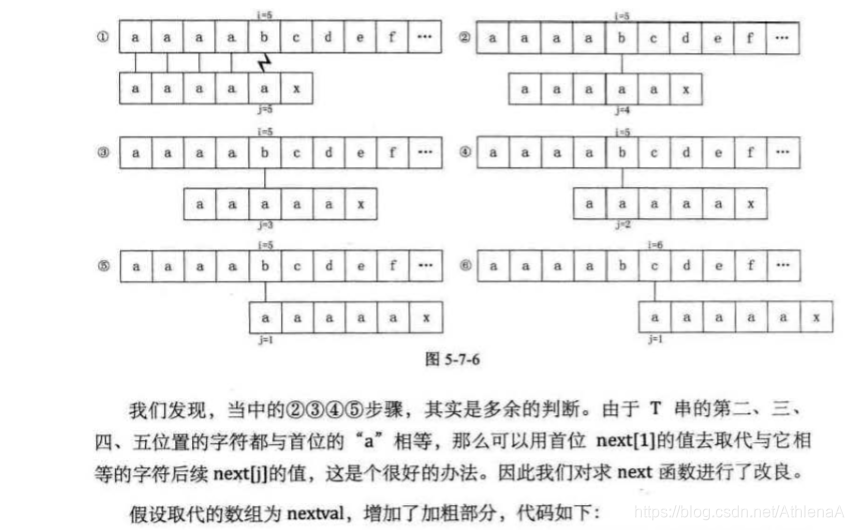
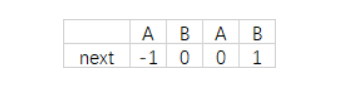
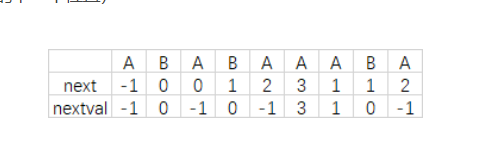
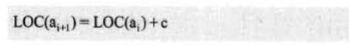第3章线性表 41
线性表:零个或多个数据元素的有限序列。
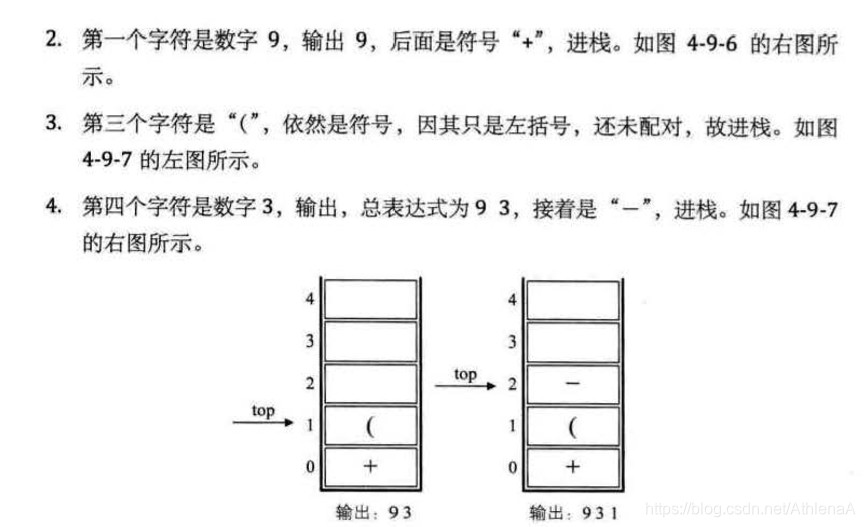
3.1开场白 42
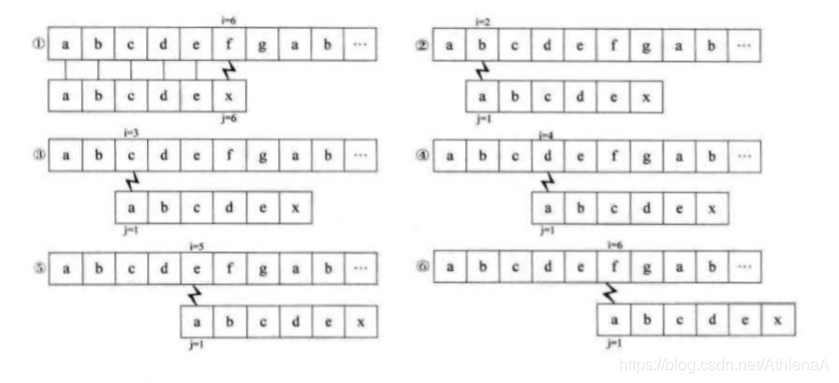
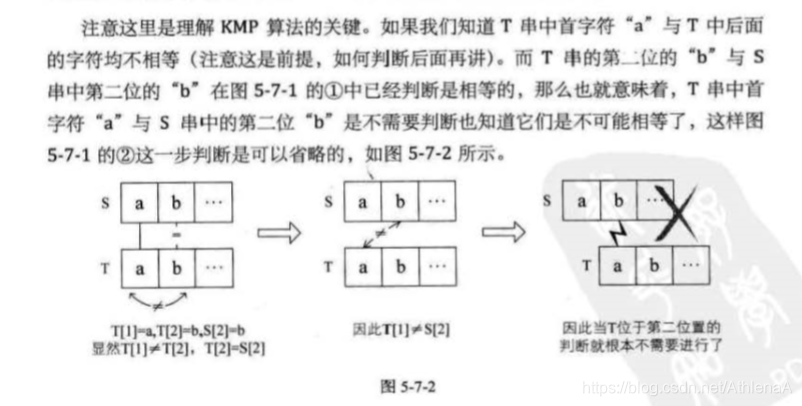
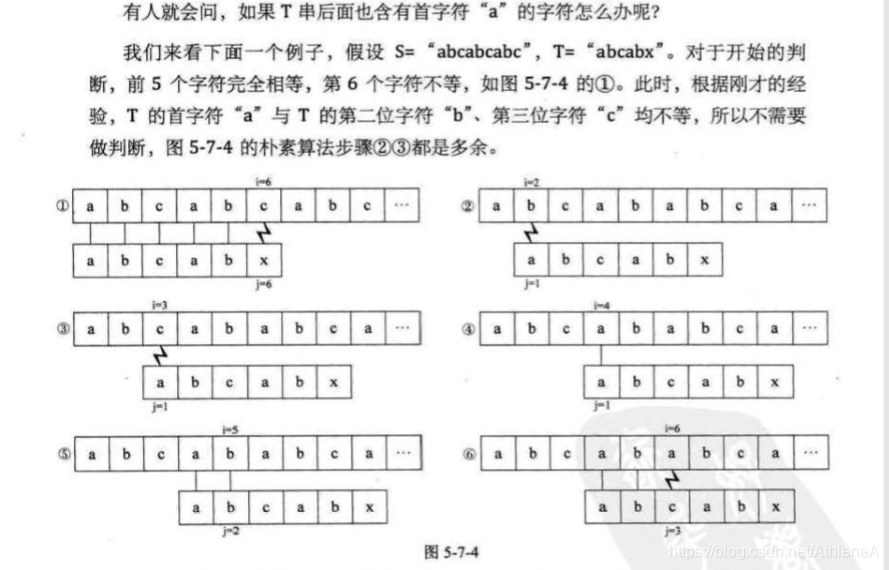
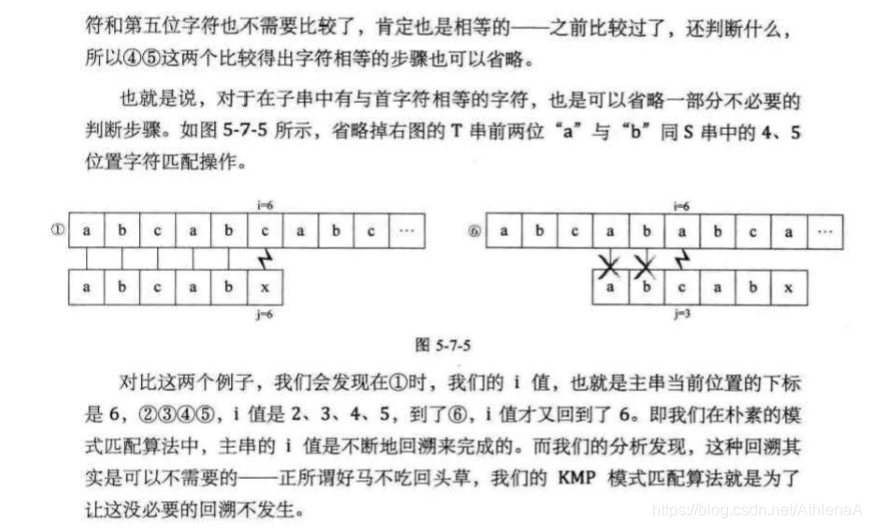
门外家长都挤在大门口与门里的小孩子的井然有序,形成了鲜明对比。哎,有时大人的所作所为,其实还不如孩子。
3.2线性表的定义 42
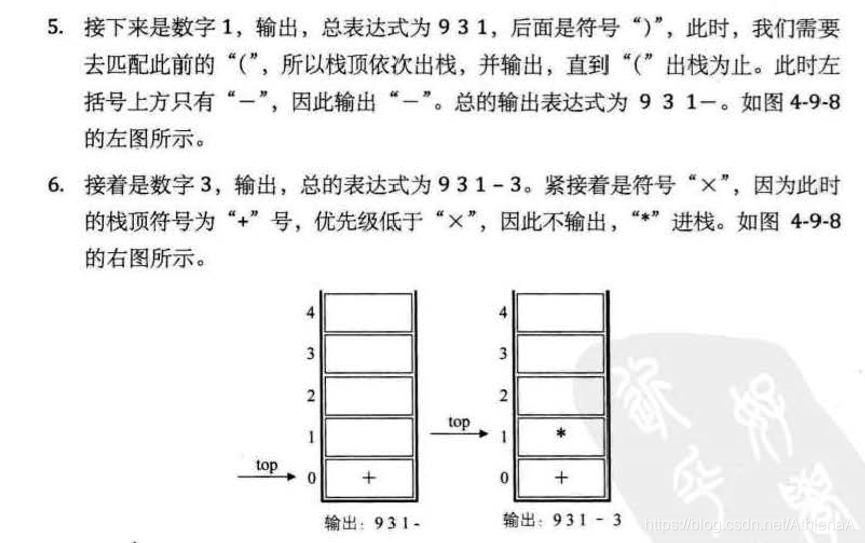
线性表(List):零个或多个数据元素的有限序列
除第一个元素外,每一个元素有且只有一个直接前驱元素,除了最后一个元素外,每一个元素有且只有一个直接后继元素,数据元素之间的关系是一对一的关系。
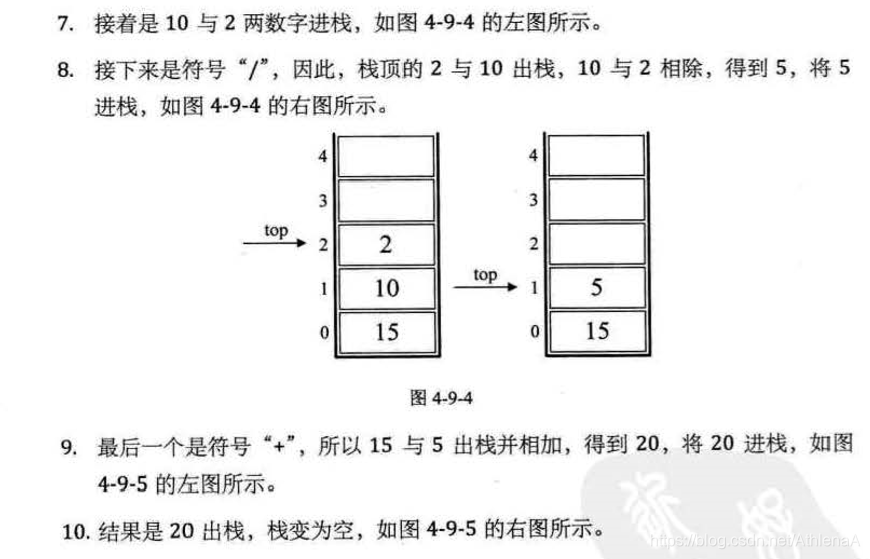
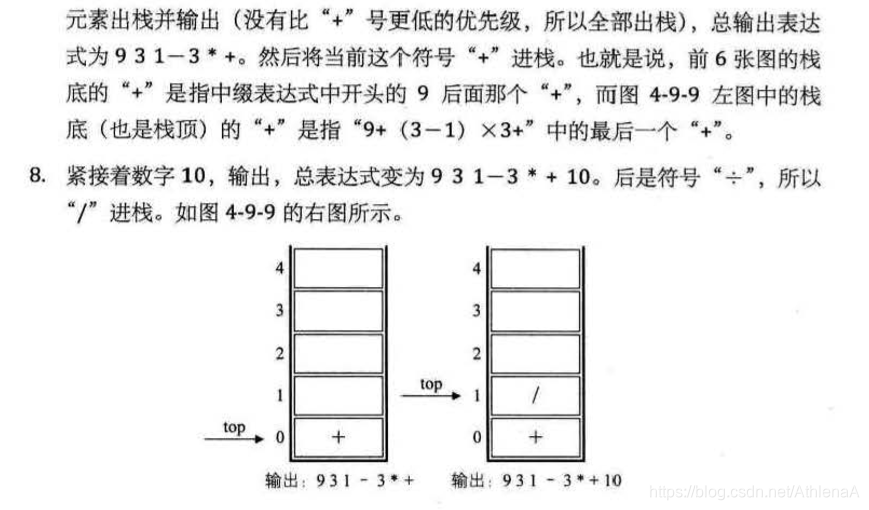
在较复杂的线性表中,一个数据元素可以由若干个数据项组成
3.3线性表的抽象数据类型 45
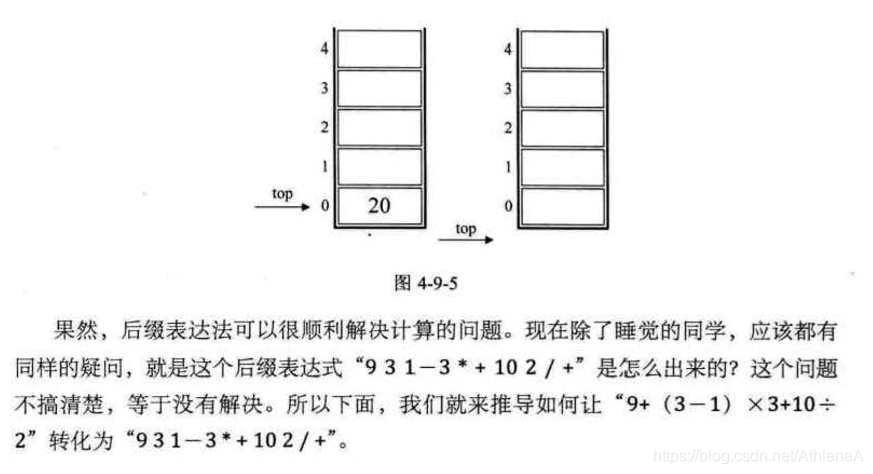
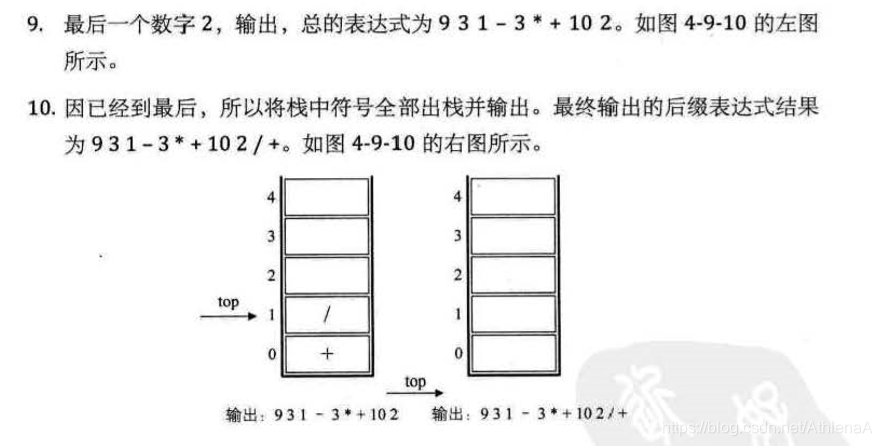
有时我们想知道某个小朋友(比如麦兜)是否是班级的同学,老师会告诉我说,没有,麦兜是在春田花花幼儿园里。这种查找某个元素是否存在的操作很常用。
线性表的创建和初始化过程.
线性表重置为空衰的操作.
以根据位序得到数据元素也是一种 很重要的线性表操作.
查找某个元 素是否存在的操作很常用。
获得线性表长度的问 题也很普遍。
插入数据和删除 数据都是必须的操作。
线性表的抽象数据类型定义如下:
要实现两个线性表集合 A 和 B 的并集操作。即要使得集合 A=AU B。 说白 了,就是把存在集合 B 中但并不存在 A 中的数据元素插入到 A 中即可。
仔细分析一下这个操作,发现我们只要循环集合 B 中的每个元素,判断当前元紫 是否存在 A 中,若不存在,则插入到 A 中即可。 思路应该是很容易想到的。
我们假设 U 表示集合 A, Lb 表示集合 8,则实现的代码如下:
这里,我们对于 union 操作,用到了前面线性表基本操作 ListLength、GetE坠m、 LocateElem、 Listlnsert 等,可见,对于复杂的个性化的操作,其实就是把基本操作组合起来实现的。
3.4线性表的顺序存储结构 47
他每次一吃完早饭就冲着去了图书馆,挑一个好地儿,把他书包里的书,一本一本的按座位放好,长长一排,九个座硬是被他占了。
3.4.1顺序存储定义 47
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。
3.4.2顺序存储方式 47
在内存中占据一定的内存空间,然后把相同数据类型的数据元素依次存放在这块空地中
既然线性表的每个数据元素的类型都相同,所以可以用 C 语言 (其他语言也相同)的一维数组来实现顺序存储结构, 即把第一个数据元素存到数组下 标为 0 的位置中,接着把线性表相邻的元素存储在数组中相邻的位置。
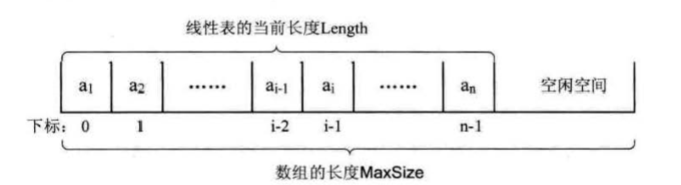
描述顺序存储结构需要三个属性:
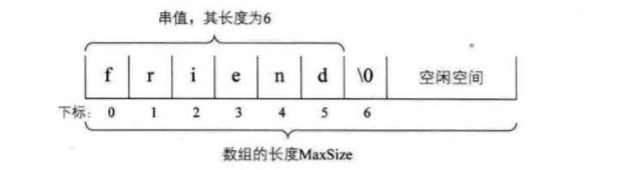
存储空间的起始位置:数组data,它的存储位置就是存储空间的存储位置
线性表的最大存储容量:数组长度MaxSize
线性表的当前长度:length
存储器中的每个存储单元都有自己的编号,这个编号称为地址
public class SqList {
private Object[] data; //存储数据元素
private int length; //线性表当前长度
private int maxSize;//数组长度,即最大储存空间
3.4.3数据长度与线性表长度区别 48
数组长度:是存放线性表的存储空间的长度,存储分配后这个量是一般是不变 的。
线性表长度:是线性表中数据元素的个数,随着线性表插入和删除操作的进行, 这个量是变化的。
在任意时刻,线性表的长度应该小于等于数组的长度。
3.4.4地址计算方法 49
可Java语言中的数组却是从 0 开始第一个下标的,于是线性表的第 i 个元素是要存储在数组 下标为 i-1 的位置,即数据元素的序号和存放它的数组下标之间存在对应关系:
用数组存储顺序表意味着要分配回走长度的数组空间,由于线位表中可以进行插 入和删除操作,因此分配的数组空间要大于等于当前线性表的长度。
存储器中的每个存储单元都有自己的编号,这个编号称为地址。
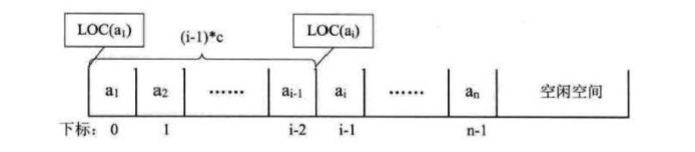
由于每个数据元素,不管它是整型、实型还是字符型,它都是需要占 用一定的存储单元空间的。假设占用的是 c 个存储单元,那么线性表中第 i+l 个数据 元素的存储位置和第 i 个数据元素的存储位置满足下列关系 (LOC 表示获得存储位置
的函数):
通过这个公式,你可以随时算出线性表中任意位置的地址,不管它是第一个还是 最后一个,都是相同的时间。 那么我们对每个线性表位置的存入或者取出数据, 对于 计算机来说都是相等的时间2 也就是一个常数,因此用我们算法中学到的时间复杂度 的概念来说,它的存取时间性能为 0(1)。我们通常把具有这一特点的存储结构称为随机存取结构。
3.5顺序存储结构的插入与删除 50
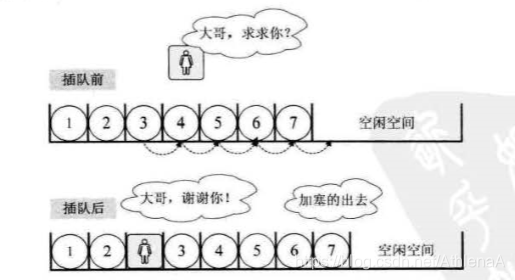
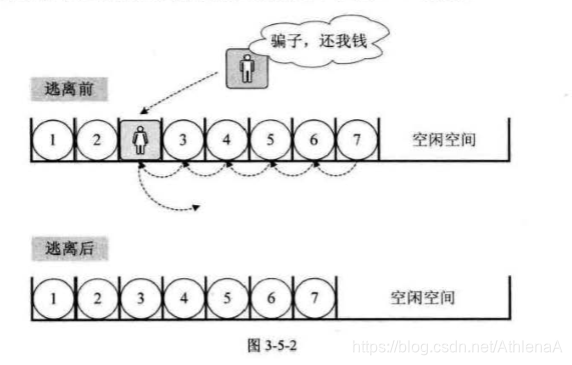
春运时去买火车票,大家都排队排着好好的,这时来了一个美女:“可否让我排在你前面?”这可不得了,后面的人像蠕虫一样,全部都得退后一步。
插入:
如果插入位置不合理,抛出异常
如果线性表长度大于等于数组长度,则抛出异常或动态增加容量
从最后一个元素开始向前遍历到第i个位置,分别将它们都向后移动一个位置
将要插入元素填入位置i处
表长加1
删除:
如果删除位置不合理,抛出异常
取出删除元素
从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一个位置
表长度减1
插入或删除时,平均移动次数和最中间的那个元素移动次数相等,为(n-1)/2
插入和删除时,时间复杂度为O(n)
3.5.1获得元素操作 50
对于统性袤的顺序存储结构来说,如果我们要实现 GetElem 操作,即将线性表 L 中的第 i 个位置元素值返回,其实是非常简单的。 就程序而言,只要 i 的数值在数组下标范围内,就是把数组第 i-l 下标的值返回即可。
/**
*获取第i个位置的元素值
*/
public E GetElem(int i) {
if(this.length==0) {
throw new RuntimeException("空表,无法获取数据!");
}
if(i<1||i>this.length) {
throw new RuntimeException("数据位置错误!");
}
System.out.println("数据获取成功!");
return (E) data[i-1];
}
时间复杂度O(1)
3.5.2插入操作 51
实现 Listlnsert (),即在线性表 L 中的第 i 个位置插入新元素 e,
数组第 i-l 下标插入新的值
线性表的顺序存储结构,在插入数据时的实现过程
插入算法的思路:
• 如果插入位置不合理,抛出异常;
• 如果线性表长度大于等于数组长度,则抛出异常或动态增加容量;
• 从最后一个元素开始向前遍历到第 i 个位置,分别将它们都向后移动一个位 置;
• 将要插入元素填入位置 i 处;
• 表长加 1。
/**
* 在第i个位置插入新元素
*/
public boolean ListInsert(int i,E e) {
if(i<1||i>this.length+1) {//如果插入位置不合理,抛出异常;
throw new RuntimeException("插入位置错误:"+i);
}
if(this.length==this.maxSize) {//如果线性表长度大于等于数组长度,则抛出异常或动态增加容量;
/*1.无法继续插入*/
//System.out.println("表已满,无法继续插入!");
//return false;
/*2.增加容量*/
maxSize=maxSize+10;
Object[] newdata=new Object[maxSize];
for (int k=1;k<=this.length;k++)
newdata[k-1]=this.data[k-1];
this.data=newdata;
}
if (i<=this.length) { //若插入数据不在表尾
for(int j=this.length-1;j>=i-1;j--) //从最后一个元素开始向前遍历到第 i 个位置,分别将它们都向后移动一个位 置;
this.data[j+1]=this.data[j];
}
this.data[i-1]=e; //将要插入元素填入位置 i 处;
this.length++; //表长加 1。
System.out.println("插入成功!");
return true;
}
最好的情况:如果元素要插入到最后一个位置, 此时时间复杂度为 O(1)。因为不需要移动元素的,就如同来了一个新人要正常排队, 当然是排在最后 , 不影响任何 人。
最坏情况 :如果元素要插入到第一个位置,那就意味着要移动所有的元素向后,所以这个时间复杂度为 O(n)。
平均的情况:由于元素插入到第 i 个位置,需要移动 n-i 个元素。 根据概率原理, 每个位置插入或删除元素的可能性是相同的,也就说位置靠 前,移动元萦多,位置靠后, 移动元素少。最终平均移动次数和最中间的那个元素的 移动次数相同,为(n-1)/2
平均时间复杂度还是 O(n)。
3.5.3删除操作 52
线性表的顺序存储结构删除元素的过程
删除算法的思路:
• 如果线性表长度为0,则不能进行删除
• 如果删除位置不合理,抛出异常
• 取出删除元素;
• 从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一 个位置;
• 表长减 1。
/**
* 删除第i个位置的元素,并用e返回其值
*/
public E ListDelete(int i) {
if(this.length==0) {//如果线性表长度为0,则不能进行删除
throw new RuntimeException("空表,无法执行删除操作!");
}
if(i<1||i>this.length) {// 如果删除位置不合理,抛出异常
throw new RuntimeException("删除位置错误!");
}
E e=(E) this.data[i-1];//取出删除元素;
if(i<this.length) { //如果删除数据不在表尾
for(int j=i;j<this.length;j++) {//从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一 个位置;
this.data[j-1]=this.data[j];
}
}
this.length--;//表长减 1。
System.out.println("删除成功!");
return e;
}
最好的情况:如果要删除最后一个元素, 此时时间复杂度为 O(1)。因为不需要移动元素的,就如同最后一个排队的人离开 , 不影响任何 人。
最坏情况 :如果要删除第一个元素,那就意味着要移动所有的元素向前,所以这个时间复杂度为 O(n)。
平均的情况:删除第 i 个位置,需要移动 n-i 个元素。 根据概率原理, 每个位置插入或删除元素的可能性是相同的,也就说位置靠 前,移动元萦多,位置靠后, 移动元素少。最终平均移动次数和最中间的那个元素的 移动次数相同,为(n-1)/2
平均时间复杂度还是 O(n)。
线性表的顺序存储结构,在存、 读数据时,不管是哪个位置,时间 复杂度都是 0(1); 而插入或删除时,时间复杂度都是 O(n)。这就说明 ,它比较适合元素个数不大变化,而更多是存取数据的应用。
3.5.4线性表顺序存储结构的优缺点 54
优点:
无须为表示表中元素之间的逻辑关系而增加额外的存储空间
可以快速地存取表中任一位置的元素
缺点:
插入和删除操作需要移动大量元素
当线性表长度变化较大时,难以确定存储空间的容量
造成存储空间的”碎片”
3.5.5 代码
package SqList;
/**
*
* 几个注意点:
* 1.初始化时,应考虑数组大小为负的情况
* 2.在各操作中,当涉及到位置i时,都应考虑i位置不合理的情况
* 3.插入操作中,需考虑线性表已满的情况
* 删除、获取操作中,需考虑线性表为空的情况
* 4.插入删除操作中,均应考虑插入或删除位置为表尾情况
* 5.插入删除操作中,别忘了最后要改变表长
*
* 几点困惑:
* 1.插入删除位置为表尾时,没有判断语句,循环部分也不会执行,判断是否在表尾会不会显得画蛇添足?
* (《大话》一书中进行了该判断)
* 2.RuntimeException类型在逻辑异常时使用,因为异常暂时还没学很好,用法是否正确?
* 3.查找元素时,是否使用equals()方法比较合适?
*
* 拓展
* 1.可进一步添加add方法,直接在表尾添加新的元素
* 2.可添加整表打印输出的方法
* @author Yongh
*
* @param <E>
*/
public class SqList<E> {
private Object[] data; //存储数据元素
private int length; //线性表当前长度
private int maxSize;//数组长度,即最大储存空间
/**
* 若初始化时未声明大小,则默认设置为20
*/
public SqList(){
//data=new Object[20];
//length=0;
/*直接利用this()更方便*/
this(20);
}
/**
* 初始化线性表
*/
public SqList(int initialSize){
if(initialSize<0) {
throw new RuntimeException("数组大小为负,初始化失败!");
}
else {
this.maxSize =initialSize;
this.data=new Object[initialSize];
this.length=0;
System.out.println("初始化成功!");
}
}
/**
* 判断线性表是否为空
*/
public boolean IsEmpty(){
if (this.length==0) {
System.out.println("表为空");
return true;
}
System.out.println("表不为空");
return false;
//return this.length==0 也可以直接这样
}
/**
* 清空线性表
*/
public void ClearList() {
this.length=0;
System.out.println("线性表已清空!");
}
/**
*获取第i个位置的元素值
*/
public E GetElem(int i) {
if(this.length==0) {
throw new RuntimeException("空表,无法获取数据!");
}
if(i<1||i>this.length) {
throw new RuntimeException("数据位置错误!");
}
System.out.println("数据获取成功!");
return (E) data[i-1];
}
/**
* 查找元素,返回值为该元素位置,0代表查找失败
*/
public int LocateElem(E e) {
for(int i=1;i<=this.length;i++) {
if(e==data[i-1]) {
System.out.println("查找成功!");
return i;
}
}
System.out.println("查找失败!");
return 0;
}
/**
* 在第i个位置插入新元素
*/
public boolean ListInsert(int i,E e) {
if(i<1||i>this.length+1) {
throw new RuntimeException("插入位置错误:"+i);
}
if(this.length==this.maxSize) {
/*1.无法继续插入*/
//System.out.println("表已满,无法继续插入!");
//return false;
/*2.增加容量*/
maxSize=maxSize+10;
Object[] newdata=new Object[maxSize];
for (int k=1;k<=this.length;k++)
newdata[k-1]=this.data[k-1];
this.data=newdata;
}
/* if (i<=this.length) { //插入数据不在表尾 **这个判断是否有必要呢?
for(int j=this.length+1;j>i;j--)
this.data[j-1]=this.data[j-2];
}*/
if (i<=this.length) { //若插入数据不在表尾
for(int j=this.length-1;j>=i-1;j--) //从最后一个元素开始向前遍历到第 i 个位置,分别将它们都向后移动一个位 置;
this.data[j+1]=this.data[j]; //0 1 2 3 4 length=5 i=4 j=4 j>3 data[5]=data[4] j=3 j=3 data[4]=data[3]
} //0 1 2 3 4 length=5 i=5 j=4 j=4 data[5]=data[4]这个算是插在末尾
this.data[i-1]=e;
this.length++; //表长改变勿忘
System.out.println("插入成功!");
return true;
}
/**
* 删除第i个位置的元素,并用e返回其值
*/
public E ListDelete(int i) {
if(this.length==0) {
throw new RuntimeException("空表,无法执行删除操作!");
}
if(i<1||i>this.length) {
throw new RuntimeException("删除位置错误!");
}
E e=(E) this.data[i-1];
if(i<this.length) { //删除数据不在表尾 **这个判断是否有必要呢?
for(int j=i;j<this.length;j++) { //0 1 2 3 4 length=5 i=4 j=4 j<5 data[3]=data[4]
this.data[j-1]=this.data[j]; //0 1 2 3 4 length=5 i=5 j=5 j!<5
}
}
this.length--;
System.out.println("删除成功!");
return e;
}
/**
* 返回线性表的元素个数
*/
public int ListLength() {
return this.length;
}
}
测试代码:
基本数据类型和引用类型各写了一个测试代码。
package SqList;
public class SqListTest {
public static void main(String[] args) {
//SqList<Integer> nums =new SqList<Integer>(-1);
SqList<Integer> nums =new SqList<Integer>(5);
nums.IsEmpty();
//System.out.println("——————————插入几个位置错误的情况——————————");
//nums.ListInsert(6, 6);
//nums.ListInsert(3, 3);
//nums.ListInsert(0, 0);
System.out.println("——————————插入1到5,并读取内容——————————");
for(int i=1;i<=5;i++)
nums.ListInsert(i, i);
nums.IsEmpty();
int num;
for(int i=1;i<=5;i++) {
num=nums.GetElem(i);
System.out.println("第"+i+"个位置的值为:"+num);
}
System.out.println("——————————查找0、5、8是否在表中——————————");
System.out.print("0的位置:");
System.out.println(nums.LocateElem(0));
System.out.print("1的位置:");
System.out.println(nums.LocateElem(1));
System.out.print("5的位置:");
System.out.println(nums.LocateElem(5));
System.out.println("——————————删除2、5——————————");
num=nums.ListDelete(2);
System.out.println("已删除:"+num);
num=nums.ListDelete(4);
System.out.println("已删除:"+num);
System.out.println("当前表长:"+nums.ListLength());
for(int i=1;i<=nums.ListLength();i++) {
num=nums.GetElem(i);
System.out.println("第"+i+"个位置的值为:"+num);
}
nums.ClearList();
nums.IsEmpty();
}
}
输出结果:
初始化成功!
表为空
——————————插入1到5,并读取内容——————————
插入成功!
插入成功!
插入成功!
插入成功!
插入成功!
表不为空
数据获取成功!
第1个位置的值为:1
数据获取成功!
第2个位置的值为:2
数据获取成功!
第3个位置的值为:3
数据获取成功!
第4个位置的值为:4
数据获取成功!
第5个位置的值为:5
——————————查找0、5、8是否在表中——————————
0的位置:查找失败!
0
1的位置:查找成功!
1
5的位置:查找成功!
5
——————————删除2、5——————————
删除成功!
已删除:2
删除成功!
已删除:5
当前表长:3
数据获取成功!
第1个位置的值为:1
数据获取成功!
第2个位置的值为:3
数据获取成功!
第3个位置的值为:4
线性表已清空!
表为空
package SqList;
public class SqListTest2 {
public static void main(String[] args) {
SqList<Student> students =new SqList<Student>();
students .IsEmpty();
System.out.println("——————————插入1到5,并读取内容——————————");
Student[] stus= {new Student("小A",11),new Student("小B",12),new Student("小C",13),
new Student("小D",14),new Student("小E",151)};
for(int i=1;i<=5;i++)
students .ListInsert(i, stus[i-1]);
students .IsEmpty();
Student stu;
for(int i=1;i<=5;i++) {
stu=students .GetElem(i);
System.out.println("第"+i+"个位置为:"+stu.name);
}
System.out.println("——————————查找小A、小E、小龙是否在表中——————————");
System.out.print("小A的位置:");
stu=stus[0];
System.out.println(students .LocateElem(stu));
System.out.print("小E的位置:");
stu=stus[4];
System.out.println(students .LocateElem(stu));
System.out.print("小龙的位置:");
stu=new Student("小龙",11);
System.out.println(students .LocateElem(stu));
System.out.println("——————————删除小E、小B——————————");
stu=students .ListDelete(2);
System.out.println("已删除:"+stu.name);
stu=students .ListDelete(4);
System.out.println("已删除:"+stu.name);
System.out.println("当前表长:"+students .ListLength());
for(int i=1;i<=students .ListLength();i++) {
stu=students .GetElem(i);
System.out.println("第"+i+"个位置为:"+stu.name);
}
students .ClearList();
students .IsEmpty();
}
}
class Student{
public Student(String name, int age) {
this.name=name;
this.age=age;
}
String name;
int age;
}
输出结果:
初始化成功!
表为空
——————————插入1到5,并读取内容——————————
插入成功!
插入成功!
插入成功!
插入成功!
插入成功!
表不为空
数据获取成功!
第1个位置为:小A
数据获取成功!
第2个位置为:小B
数据获取成功!
第3个位置为:小C
数据获取成功!
第4个位置为:小D
数据获取成功!
第5个位置为:小E
——————————查找小A、小E、小龙是否在表中——————————
小A的位置:查找成功!
1
小E的位置:查找成功!
5
小龙的位置:查找失败!
0
——————————删除小E、小B——————————
删除成功!
已删除:小B
删除成功!
已删除:小E
当前表长:3
数据获取成功!
第1个位置为:小A
数据获取成功!
第2个位置为:小C
数据获取成功!
第3个位置为:小D
线性表已清空!
表为空
3.6线性表的链式存储结构 55
反正也是要让相邻元素间留有足够余地,那干脆所有元素都不要考虑相邻位置了,哪有空位就到哪里。而只是让每个元素知道它下一个元素的位置在哪里。
在内存中将好友按顺序号从小到大返回,不允许查数据库,就可以使用链表。
以上是实际结构。
以下是逻辑结构。
使用带head头的单向链表实现 –水浒英雄排行榜管理
完成对英雄人物的增删改查操作, 注: 删除和修改,查找
第一种方法在添加英雄时,直接添加到链表的尾部
第二种方式在添加英雄时,根据排名将英雄插入到指定位置(如果有这个排名,则添加失败,并给出提示)
单链表的常见面试题有如下:
求单链表中有效节点的个数
查找单链表中的倒数第k个结点 【新浪面试题】
单链表的反转【腾讯面试题,有点难度】
从尾到头打印单链表 【百度,要求方式1:反向遍历 。 方式2:Stack栈】
合并两个有序的单链表,合并之后的链表依然有序【课后练习.】
思路:创建一个新的链表,发现哪个更小就把哪个节点加进去
package com.zcr.linkedlist;
import java.net.HttpRetryException;
import java.util.Stack;
/**
* @author zcr
* @date 2019/7/5-10:21
*/
public class SingleLinkedListDemo {
public static void main(String[] args) {
//先创建几个节点
HeroNode hero1 = new HeroNode(1,"宋江","及时雨 ");
HeroNode hero2 = new HeroNode(2,"卢俊义","玉麒麟");
HeroNode hero3 = new HeroNode(3,"吴用","智多星");
HeroNode hero4 = new HeroNode(4,"林冲","豹子头");
//创建单链表
SingleLinkedList singleLinkedList = new SingleLinkedList();
/*singleLinkedList.add(hero1);
singleLinkedList.add(hero4);
singleLinkedList.add(hero2);
singleLinkedList.add(hero3);*/
//按照编号的顺序添加
singleLinkedList.addByOrder(hero1);
singleLinkedList.addByOrder(hero4);
singleLinkedList.addByOrder(hero2);
singleLinkedList.addByOrder(hero3);
singleLinkedList.addByOrder(hero2);
singleLinkedList.list();
//修改节点信息
HeroNode newHeroNode = new HeroNode(2,"小卢","小于");
singleLinkedList.update(newHeroNode);
System.out.println("修改后的链表:");
singleLinkedList.list();
//删除节点
singleLinkedList.delete(1);
singleLinkedList.delete(4);
System.out.println("删除后的链表:");
singleLinkedList.list();
//求单链表中有效节点的个数
System.out.println("有效的节点个数有:"+SingleLinkedList.getLength(singleLinkedList.getHead()));
//得到倒数第k个元素
HeroNode res = SingleLinkedList.findLastIndexNode(singleLinkedList.getHead(),2);
System.out.println("res:"+res);
//单链表的反转
/*System.out.println("原链表为:");
singleLinkedList.list();
System.out.println("反转后的链表为:");
SingleLinkedList.reverseList(singleLinkedList.getHead());
singleLinkedList.list();*/
//逆序打印
System.out.println("将链表逆序打印:");
SingleLinkedList.reversePrint(singleLinkedList.getHead());
}
}
//定义HeroNode,每个HeroNode对象就是一个节点
class HeroNode {
public int no;
public String name;
public String nickname;
public HeroNode next;//指向下一个节点
//构造器
public HeroNode(int no,String name,String nickname) {
this.no = no;
this.name = name;
this.nickname = nickname;
}
//为了显示方便,重写toString
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
", nickname='" + nickname + '\'' +
//", next=" + next +这个nect域不要打印了,否则每次一连串都会打印出来
'}';
}
}
//定义SingLinkedList管理我们的英雄
class SingleLinkedList {
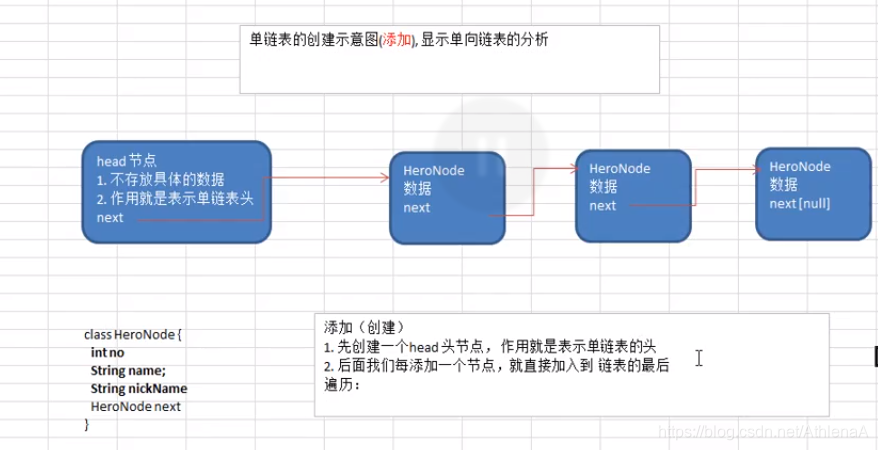
//先初始化一个头结点,头结点不要动,不存放具体的数据
private HeroNode head = new HeroNode(0,"","");
//返回头结点
public HeroNode getHead() {
return head;
}
//添加节点到单向链表
//思路,当不考虑编号顺序时,找到最后一个节点,把它的next域指向新的节点
public void add(HeroNode heroNode) {
//因为head节点不能动,因此我们需要一个辅助变量temp
HeroNode temp = head;
/*while (temp != null){
temp = temp.next;
}
temp.next = heroNode;*/
while (true) {
//找到链表的最后
if (temp.next == null){
break;
}
//如果没有找到最后,将temp后移
temp = temp.next;
}
//当退出while循环时,temp就指向了链表的最后
temp.next = heroNode;//第一次用的时候发生了空指针异常,因为我用了空对象去调用方法和属性
}
//第二种方式在添加英雄时,根据排名将英雄插入到指定位置
//如果有这个排名,则添加失败,并给出提示
//就可以在内存中把顺序排好,比数据库中肯定要快
//因为头结点不能动,因此我们仍然通过一个辅助变量来帮助找到添加位置
//因此我们找的temp是位于添加位置的前一个节点,否则插入不了
//说明我们在比较时,是temp.next.no和需要插入的节点的no做比较
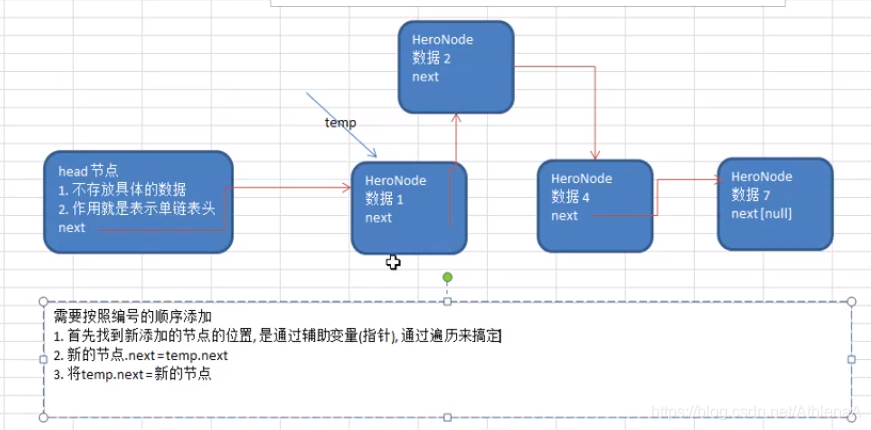
public void addByOrder(HeroNode heroNode) {
HeroNode temp = head;
boolean flag = false;//标识添加的编号是否存在,默认为false
while (true) {
if (temp.next == null){//说明temp已经在链表的最后
break;
}
if (temp.next.no > heroNode.no) {//位置找到,就在temo的后面插入
break;
} else if (temp.next.no == heroNode.no) {//说明希望添加的heroNode的编号已经存在了
flag = true;
break;
}
temp =temp.next;//后移,遍历当前的链表
}
if (flag) {//不能添加,说明编号存在
System.out.printf("准备插入的英雄的编号%d已经存在,不能加入\n",heroNode.no);
} else {
//插入到链表中,temp的后边
heroNode.next = temp.next;
temp.next = heroNode;
}
}
//完成修改节点的信息,根据编号来修改,即编号不能改
public void update(HeroNode newHeroNode) {
//判断链表是否为空
if (head.next == null){
System.out.println("链表为空");
return;
}
//找到需要修改的节点,根据编号找
//先定义一个辅助变量
HeroNode temp = head.next;
boolean flag = false;//是否找到该节点
while (true) {
if (temp == null){
break;//到链表的最后的下一个节点了,已经遍历结束了
}
if (temp.no == newHeroNode.no) {//找到了
flag = true;
break;
}
temp = temp.next;
}
//根据flag判断是否找到要修改的节点
if (flag) {
temp.name = newHeroNode.name;
temp.nickname =newHeroNode.nickname;
} else {//没有找到
System.out.printf("没有找到编号为%d的节点,不能修改\n",newHeroNode.no);
}
}
//删除节点
//因为头结点不能动,因此我们仍然通过一个辅助变量来帮助找到添加位置
//因此我们找的temp是位于添加位置的前一个节点,否则删除不了
//说明我们在比较时,是temp.next.no和需要删除的节点的no做比较
public void delete(int no) {
HeroNode temp = head;
boolean flag = false;//是否找到待删除节点的前一个节点
while (true) {
if (temp.next == null) {
break;
}
if (temp.next.no == no){
flag = true;//找到了待删除节点的前一个节点
break;
}
temp = temp.next;
}
if (flag) {
temp.next = temp.next.next;
} else {
System.out.printf("要删除的节点%d不存在\n",no);
}
}
//显示链表,通过遍历
public void list() {
//判断链表是否为空
if(head.next == null) {
System.out.println("链表为空");
return;
}
//因为头结点不能动,因此我们需要一个辅助变量来遍历
HeroNode temp = head.next;
while(true){
//判断是否到链表最后
if (temp == null){
break;
}
//输出节点信息
System.out.println(temp);
//将temp后移
temp = temp.next;
}
}
//获取单链表的节点的个数
// (如果是带头结点的链表,需要补统计头结点)
/**
*
* @param head 链表的头结点
* @return 返回的是有效节点的个数
*/
public static int getLength(HeroNode head) {
if (head.next == null) {//空链表
return 0;
}
int length = 0;
//定义一个辅助的变量
HeroNode cur = head.next;//这里没有统计头结点
while (cur != null){
length++;
cur = cur.next;
}
return length;
}
//查找单链表中的倒数第K个节点
//接收head节点,同时接收index(倒数第index个节点);
//把链表从头到尾遍历得到链表的长度;调用getLength()
//用size-index,从链表的第一个开始遍历(size-index)个就可得
public static HeroNode findLastIndexNode(HeroNode head,int index) {
//判断链表为空,返回null
if (head.next == null){
return null;//没有在找到
}
//第一个遍历得到链表的长度
int size = getLength(head);
//第二次遍历size-index位置,就是我们倒数第k个节点
//先做一个index的校验
if (index <= 0 || index > size){
return null;
}
//定义一个辅助变量
HeroNode cur = head.next;
for (int i = 0; i < size-index; i++) {
cur = cur.next;
}
return cur;
}
//将单链表进行反转
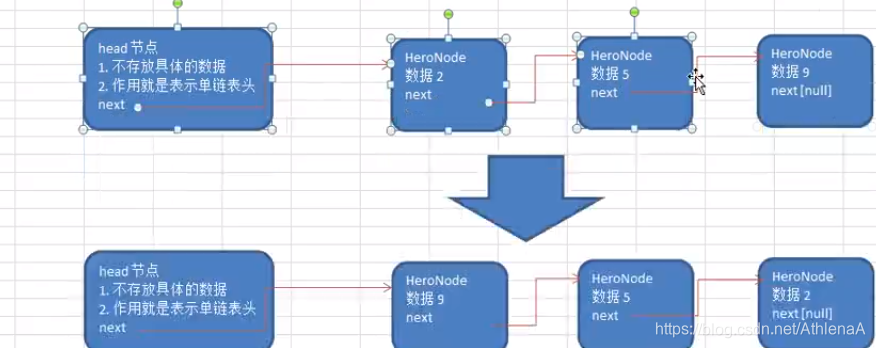
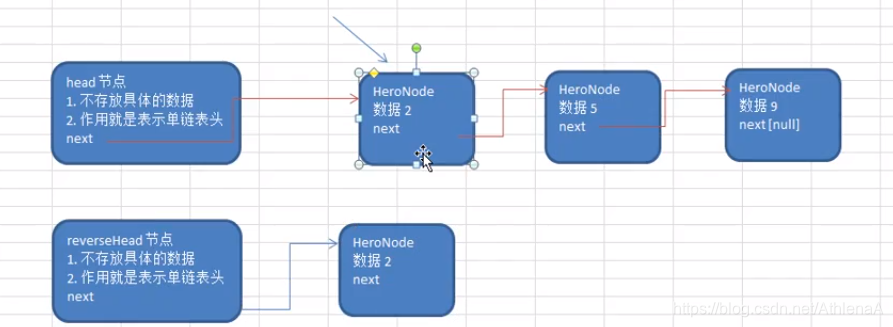
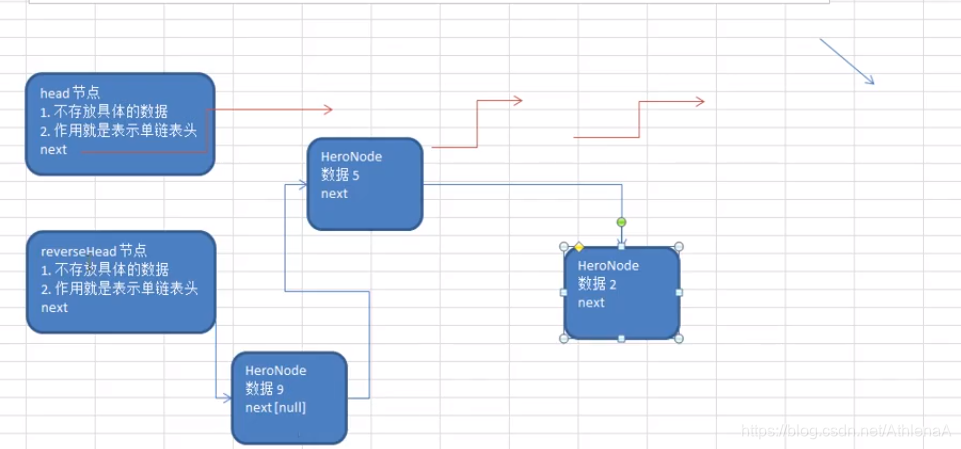
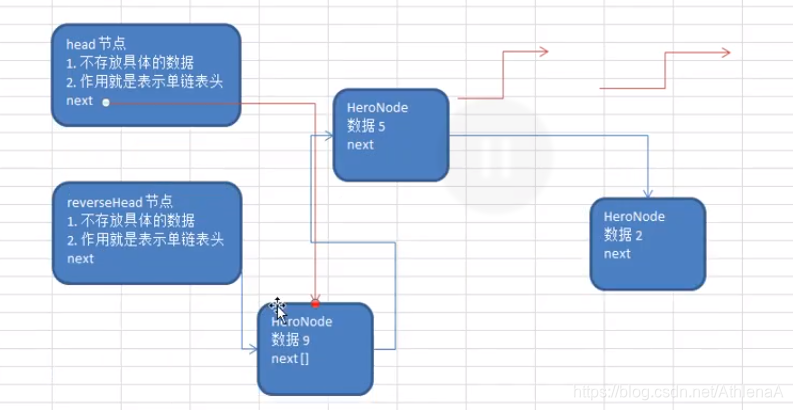
public static void reverseList(HeroNode head) {
//如果当前连标王为空或者只有一个节点,无需反转直接返回
if (head.next == null || head.next.next == null) {
return ;
}
//定义一个辅助变量,作用:帮助我们遍历原来的链表
HeroNode cur = head.next;
//指向当前节点的下一个节点
HeroNode next = null;
//定义反转链表的头结点
HeroNode reverseHead = new HeroNode(0,"","");
//开始遍历原来的链表,并完成反转工作
//每遍历一个节点,就将其取出,并放在新的链表中
while (cur != null) {
next = cur.next;//先暂时保存当前节点的下一个节点,因为后面要用
cur.next = reverseHead.next;//将cur的下一个节点指向新的链表的头部
reverseHead.next = cur;//新链表的头部
cur = next;//让cur后移
}
head.next = reverseHead.next;
}
//逆序打印
//可以使用栈这个数据结构
public static void reversePrint(HeroNode head) {
if(head.next == null){
return;//空链表不能打印
}
//创建一个栈,将各个节点压入栈中
Stack<HeroNode> stack = new Stack<HeroNode>();
HeroNode cur = head.next;
//将链表的所有节点压入栈中
while(cur != null) {
stack.push(cur);
cur = cur.next;
}
//将栈中的节点进行打印,出栈
while (stack.size() > 0){
System.out.println(stack.pop());
}
}
}
3.6.1顺序存储结构不足的解决办法 55
线性表的顺序存储结构。它是有缺点的,最大的缺点就是插入和删除时需要移动大量元素。
要解决这个问题,我们就得考虑一下导致这个问题的原因.
为什么当插入和删除时,就要移动大量元素,仔细分析后,发现原因就在于相邻 两元素的存储位置也具有邻居关系。它们编号是 1, 2, 3,…, n ,它们在内存中的位 置也是挨着的,中间没有空隙, 当然就无法快速介入,而删除后, 当中就会留出空 隙,自然需要弥补。问题就出在这里。
我们反正也是要让相邻元素间留有足够余地,那干脆所有的元素都 不要考虑相邻位置了,哪有空位就到哪里,而只是让每个元素知道包下一个元素的位 置在哪里,这样,我们可以在第一个元素时,就知道第二个元素的位置(内存地址) , 而找到包 ; 在第二个元素时,再找到第三个元素的位置(内存地址)。这样所有的元素 我们就都可以通过遍历而找到。
3.6.2线性表链式存储结构定义 56
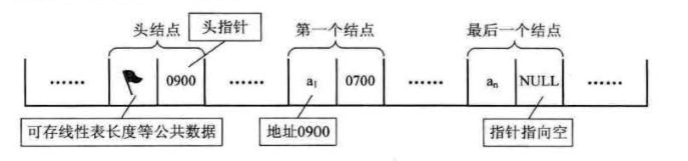
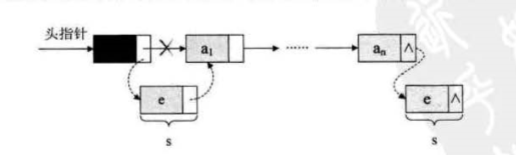
线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的,这就意味着,这些数据元素可以存在内存未被占用的任意位置
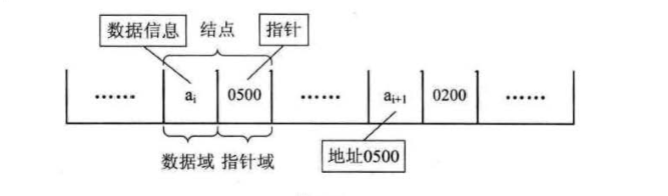
链式结构中,除了要存储数据元素信息外,还要存储它的后继元素的存储地址
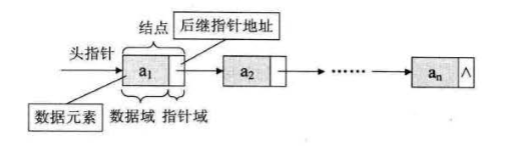
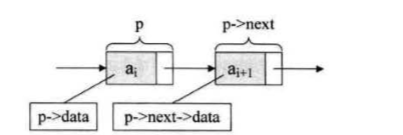
我们把存储数据元素信息的域称为数据域, 把存储直接后 继位置的域称为指针域。 指针域中存储的信息称做指针或链。 这两部分信息组成数据 元素 ai 的存储映像,称为结点 (Node)。
n 个结点 (al 的存储映像) 链结成一个链衰,即为线性表 (a1, a2,…, an) 的链 式存储结构,因为此链表的每个结点中只包含一个指针域,所以叫做单链表。单链表 正是通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起:
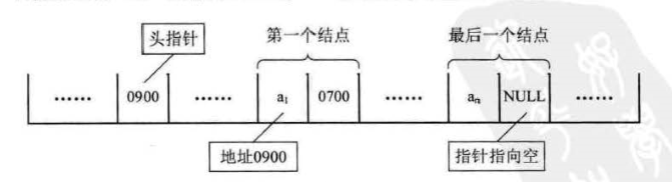
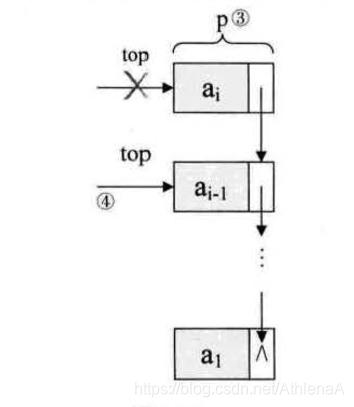
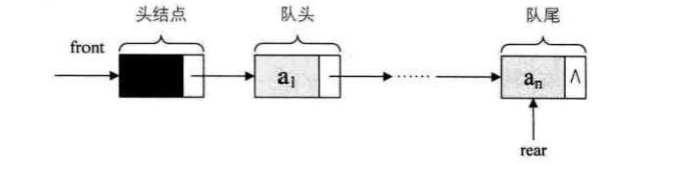
链表中第一个结点的存储位置叫做头指针,那么整个链袤的存取就必须是从头指针开始进行了 。 之后的每一个结点,其实就是上一个的后继指针指向的位置,最后一个结点的指针为null。
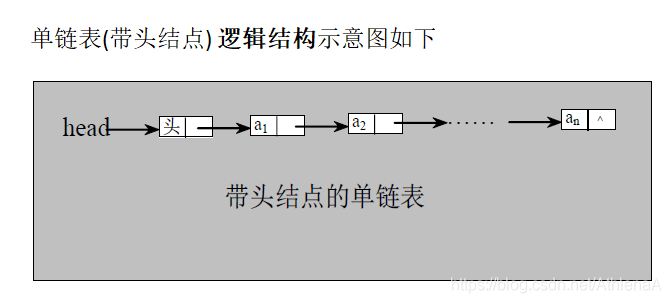
为了更加方便地对链表进行操作,有时会在单链表的第一个结点前附设一个结点,称为头结点,头结点的数据域可以不存储任何信息,也可以存储如线性表的长度等附加信息,头结点的指针域存储指向第一个结点的指针
3.6.3头指针与头结点的异同 58
头指针与头结点的异同:
头指针是指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针
头指针具有标识作用,所以常用头指针冠以链表的名字
无论链表是否为空,头指针均不为空,头指针是链表的必要元素
头结点是为了操作的统一和方便而设立的,放在第一元素的结点之前,其数据域一般无意义(也可存放链表的长度)
有了头结点,对在第一元素结点前插入结点和删除第一结点,其操作与其它结点的操作就统一了
头结点不一定是链表必须要素
3.6.4线性表链式存储结构代码描述 58
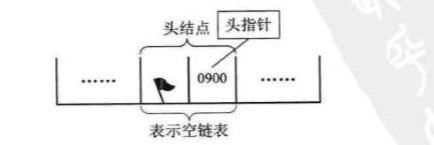
若钱’性表为空袭,则头结点的指针域为"空",
这里我们大概地用图示表达了内存中单链表的存储状态。看着满图的省略号 “……” ,你就知道是多么不方便。而我们真正关心的:它是在内存中的实际位置吗? 不是的,这只是它所表示的线性表中的数据元素及数据元素之间的逻辑关系。所以我 们改用更方便的存储示意图来表示单链表:
若带有头结点的单链表:
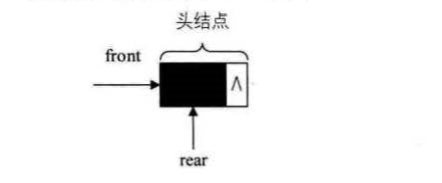
空链表:
public class LinkList<E> {
private Node<E> head; //头结点
private int count; //线性表长度(《大话》存储于head.data中)
/**
* 结点
*/
private class Node<E>{
E data;
Node<E> next;
public Node(E data,Node<E> next){
this.data=data;
this.next=next;
}
}
/**
* 线性表的初始化
*/
public LinkList(){
head=new Node<E>(null, null); //不是head=null;
count=0;
}
结点由:存放数据元素的数据域存放后继结点地址的指针域组成。
3.7单链表的读取 60
单链表中查找某一个元素,必须要从头开始找
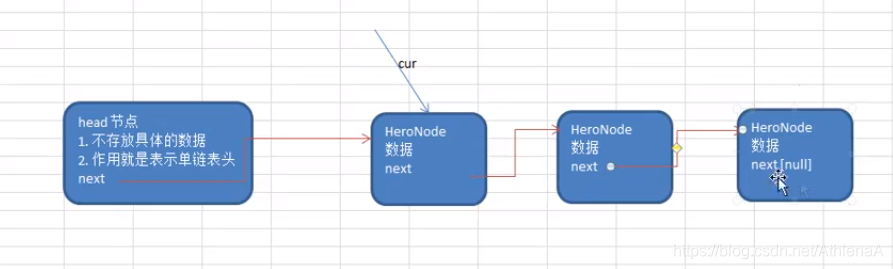
获得链表第i个数据的算法思路:
1.声明一个结点p指向链表第一个结点,初始化j从1开始
2.当j<i时,就遍历链表,让p的指针向后移动,不断指向下一结点,j累加1,
3.若到链表末尾p为空,则说明第i个元素不存在
4.否则查找成功,返回结点p的数据
时间复杂度为O(n)
/**
* 获取第i个结点(包括第0个结点,头结点)
* 获取结点值只需要GetNode(i).data即可,不再写方法了
*/
public Node<E> GetNode(int i) {
if(i<0||i>count) {
throw new RuntimeException("元素位置错误!");
}else if (i==0) {
return head;
}else {
Node<E> node=head.next;
for(int k=1;k<i;k++) {
node=node.next;
}
return node;
}
}
/**
* 获取第i个结点的数据(包括头结点)
*/
public E GetData(int i) {
return GetNode(i).data;
}
说白了,就是从头开始找,直到第 i 个元素为止。由于这个算法的时间复杂度取 决于 i 的位置,当 i=l 时,则不需遍历,第一个就取出数据了,而当 i=n 时则遍历 n-1 次才可以。 因此最坏情况的时间复杂度是 O(n)。
3.8单链表的插入与删除 61
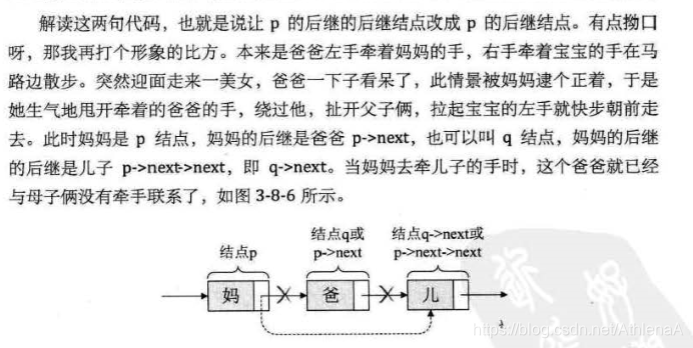
本来是爸爸左牵着妈妈的手、右牵着宝宝的手在马路边散步。突然迎面走来一美女,爸爸失神般地望着,此情景被妈妈逮个正着,于是扯开父子俩,拉起宝宝的左手就快步朝前走去。
3.8.1单链表的插入 61
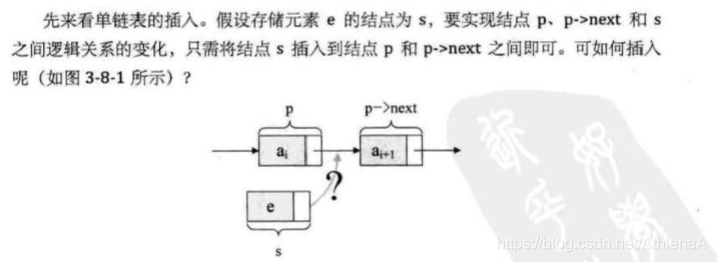
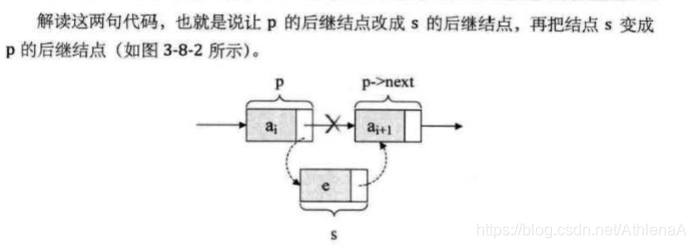
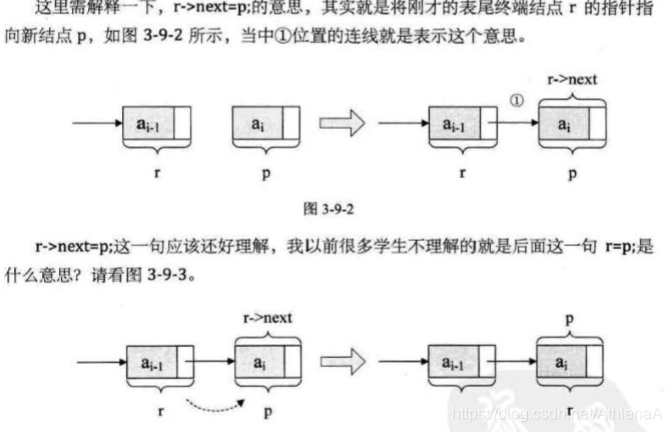
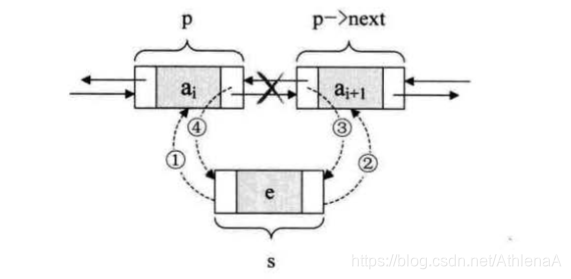
在ai和ai+1之间插入一个数据,只需要
s->next=p->next;
p->next=s;
对于单链裴的表头和表尾的特殊情况,操作是相同的:
单链表第i个数据插入结点的算法思路:
1.声明一结点p指向链表第一个结点,初始化j从1开始
2.当j<i时,就遍历链表,让p的指针向后移动,不断指向下一结点,j累加1
3.若到链表末尾p为空,则说明第i个元素不存在
4.否则查找成功,在系统中生成一个空结点s
5.将数据元素e赋值给s->data
6.单链表的插入标准语句s->next=p->next;p->next=s;
7.返回成功
/**
* 第i个位置插入新的元素
*/
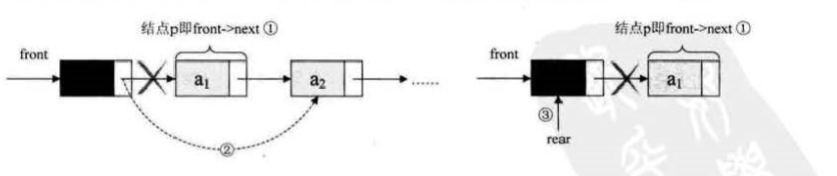
public void ListInsert(int i,E e) {
if(i<1||i>count+1) {
throw new RuntimeException("插入位置错误!");
}else {
Node<E> newNode=new Node<E>(e,null);
newNode.next=GetNode(i-1).next; //因为GetNode()方法中包含了获取头结点,所以不需单独判断了
GetNode(i-1).next=newNode;
count++;
System.out.println("插入成功!");
}
}
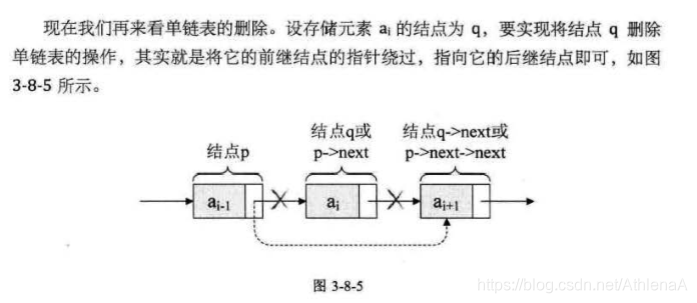
3.8.2单链表的删除 64
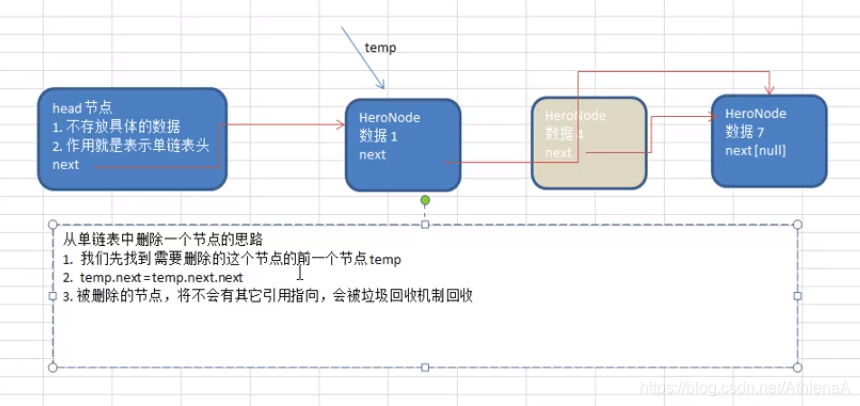
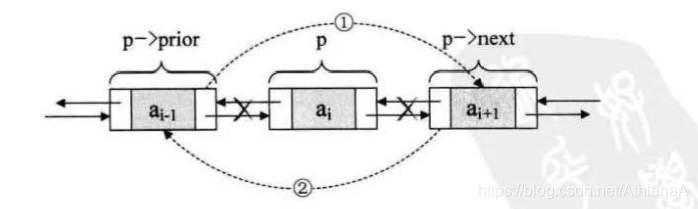
在ai-1和ai+1之间删除ai结点,只需要
q=p->next;
p->next=q->next;
单链表第i个数据删除结点的算法思路:
1.声明一结点p指向链表第一个结点,初始化j从1开始
2.当j<i时,就遍历链表,让p的指针向后移动,不断指向下一个节点,j累加1
3.若到链表末尾p为空,则说明第i个元素不存在
4.否则查找成功,将欲删除的结点p->next赋值给q
5.单链表的删除标准语句p->next=q->next
6.将q结点中的数据赋值给e,作为返回
7.释放q结点
8.返回成功
/**
* 删除第i个位置元素,并返回其值
*/
public E ListDelete(int i) {
if(i<1||i>count)
throw new RuntimeException("删除位置错误!");
Node<E> node=GetNode(i);
E e=node.data;
GetNode(i-1).next=node.next;
node=null;
count--;
System.out.println("删除成功!");
return e;
}
分析一下刚才我们讲解的单链表插入和删除算法,我们发现,官们其实都是由两 部分组成;第一部分就是遍历查找第 i 个元素;第二部分就是插入和删除元素。
单链表在查询、插入和删除操作上的时间复杂度都是O(n),。如果在我们 不知道第 1 个元素的指针位置,星在链表数据结构在插入和删除操作上,与线性表的顺 序存储结构是没有太大优势的。但是如果需要从第i个位置,插入10个元素,对于顺序存储结构意味着,每一次插入都需要移动n-i个元素,每次都是O(n),而单链表,只需要在第一次时,找到第i个位置的指针,此时为O(n),接下来的时间复杂度都是O(1),所以对于插入或者删除数据越频繁的操作,单链表的效率优势就越是明显。
3.9单链表的整表创建 66
顺序存储结构的创建,其实就是一个数组的初始化,即声明一个类型 和大小的数组并赋值的过程。而单链表和顺序存储结构就不一样,它不像顺序存储结 构这么集中,官可以很散,是一种动态结构。对于每个链表来说,它所占用空间的大 小和位置是不需要预先分配划定的,可以根据系统的情况和实际的需求即时生成。
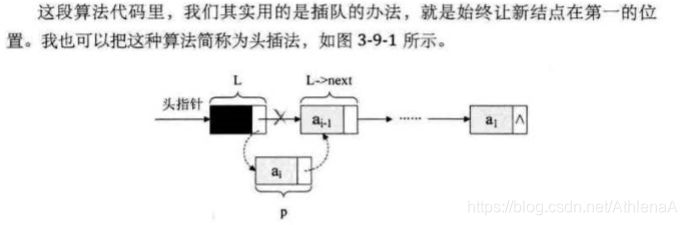
所以创建单链表的过程就是一个动态、生成链表的过程。即从"空表"的初始状态起,依次建立各元素结点,并逐个插入链表。
单链表整表创建的算法思路:
1.声明一结点p和计数器变量i
2.初始化一空链表L
3.让L的头结点的指针指向NULL,即建立一个带头结点的单链表
4.循环:
生成一新结点赋值给p
随机生成一数字赋值给p的数据域p->data
将p插入到头结点与前一新结点之间(头插法,始终让新结点在第一的位置),也可以将p插入到终端结点的后面(尾插法)
/**
* 整表创建,头插法
*/
public LinkList<Integer> CreateListHead(int n){
LinkList<Integer> list1=new LinkList<Integer>();
Node<Integer> node,lastNode;
for(int i=0;i<n;i++) {
int data=(int)(Math.random()*100); //生成100以内的随机数
node=new Node<Integer>(data, null);
node.next=(LinkList<E>.Node<Integer>) list1.head.next;
list1.head.next=(LinkList<Integer>.Node<Integer>) node;
list1.count++;
}
return list1;
}
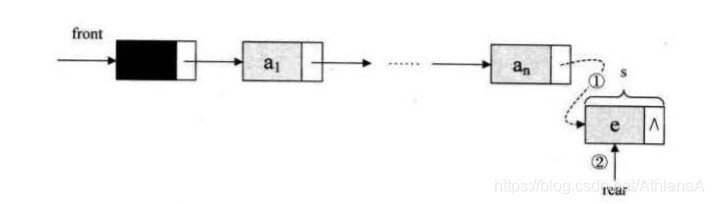
我们把每次新结点都插在终端结点的后面,这种 算法称之为尾插法。
/**
* 整表创建,尾插法
*/
public LinkList<Integer> CreateListTail(int n){
LinkList<Integer> list2=new LinkList<Integer>();
Node<Integer> node,lastNode;
lastNode=(LinkList<E>.Node<Integer>) list2.head;
for(int i=0;i<n;i++) {
int data=(int)(Math.random()*100); //生成100以内的随机数
node=new Node<Integer>(data, null);
lastNode.next=node;
lastNode=node;
list2.count++;
}
lastNode.next=null;
return list2;
}
注意 list2与 lastnode 的关系, list2 是指整个单链衰,而 lastnode是指向尾结点的变量, lastnode 会随着循环 不断地变化结点,而 list2 则是随着循环增长为一个多结点的链表。
3.10单链表的整表删除 69
单链表整表删除的算法思路如下:
1.声明一结点p和q
2.将第一个结点赋值给p
3.循环
将下一结点赋值给q
释放p
将q赋值给p
/**
* 清空线性表(自己编写的)
*/
public void ClearList() {
Node<E> node;
while(count!=0) {
node=head.next;
head.next=node.next;
node=null;
count--;
}
System.out.println("线性表已清空!");
}
/**
* 清空线性表(书中改写)
*/
public void ClearList2() {
Node<E> q,p;
q=head.next;
while(q!=null) {
p=q.next;
q=null;
q=p;
count--;
}
head.next=null;
System.out.println("线性表已清空!");
}
单链表代码
package LinkList;
/**
* 说明:
* 1.《大话数据结构》中没有线性表的长度,但提到可以存储于头节点的数据域中。
* 本程序的线性表长度存放于count变量中,线性表长度可以使程序比较方便。
* 2.程序中,第i个位置代表第i个结点,头结点属于第0个结点
* 3.因为链表为泛型,整表创建采用整型(随机整数做元素),所以有出现一些类型转换
* 4.Java程序的方法一般以小写开头,但为和书上一致,程序中方法采用了大写开头。
*
* 注意点:
* 1.count在增删元素时要加一或减一千万别忘了
* 2.清空线性表要每个元素都null
*
* @author Yongh
*
*/
public class LinkList<E> {
private Node<E> head; //头结点
private int count; //线性表长度(《大话》存储于head.data中)
/**
* 结点
*/
private class Node<E>{
E data;
Node<E> next;
public Node(E data,Node<E> next){
this.data=data;
this.next=next;
}
}
/**
* 线性表的初始化
*/
public LinkList(){
head=new Node<E>(null, null); //不是head=null;
count=0;
}
/**
* 判断线性表是否为空
*/
public boolean IsEmpty() {
if(count==0) {
System.out.println("表为空!");
return true;
}else {
System.out.println("表不为空!");
return false;
}
//return count==0;
}
/**
* 清空线性表(自己编写的)
*/
public void ClearList() {
Node<E> node;
while(count!=0) {
node=head.next;
head.next=node.next;
node=null;
count--;
}
System.out.println("线性表已清空!");
}
/**
* 清空线性表(书中改写)
*/
public void ClearList2() {
Node<E> q,p;
q=head.next;
while(q!=null) {
p=q.next;
q=null;
q=p;
count--;
}
head.next=null;
System.out.println("线性表已清空!");
}
/**
* 获取第i个结点(包括第0个结点,头结点)
* 获取结点值只需要GetNode(i).data即可,不再写方法了
*/
public Node<E> GetNode(int i) {
if(i<0||i>count) {
throw new RuntimeException("元素位置错误!");
}else if (i==0) {
return head;
}else {
Node<E> node=head.next;
for(int k=1;k<i;k++) {
node=node.next;
}
return node;
}
}
/**
* 获取第i个结点的数据(包括头结点)
*/
public E GetData(int i) {
return GetNode(i).data;
}
/**
* 查找元素,0代表查找失败
*/
public int LocateElem(E e) {
Node<E> node;
node=head.next;
if(node.data==e)
return 1;
for(int k=1;k<count;k++) {
node=node.next;
if(node.data==e)
return k+1;
}
System.out.println("查找失败!");
return 0;
}
/**
* 第i个位置插入新的元素
*/
public void ListInsert(int i,E e) {
if(i<1||i>count+1) {
throw new RuntimeException("插入位置错误!");
}else {
Node<E> newNode=new Node<E>(e,null);
newNode.next=GetNode(i-1).next; //因为GetNode()方法中包含了获取头结点,所以不需单独判断了
GetNode(i-1).next=newNode;
count++;
System.out.println("插入成功!");
}
}
/**
* 删除第i个位置元素,并返回其值
*/
public E ListDelete(int i) {
if(i<1||i>count)
throw new RuntimeException("删除位置错误!");
Node<E> node=GetNode(i);
E e=node.data;
GetNode(i-1).next=node.next;
node=null;
count--;
System.out.println("删除成功!");
return e;
}
/**
* 获取线性表长度
*/
public int ListLength() {
return count;
}
/**
* 整表创建,头插法
*/
public LinkList<Integer> CreateListHead(int n){
LinkList<Integer> list1=new LinkList<Integer>();
Node<Integer> node,lastNode;
for(int i=0;i<n;i++) {
int data=(int)(Math.random()*100); //生成100以内的随机数
node=new Node<Integer>(data, null);
node.next=(LinkList<E>.Node<Integer>) list1.head.next;
list1.head.next=(LinkList<Integer>.Node<Integer>) node;
list1.count++;
}
return list1;
}
/**
* 整表创建,尾插法
*/
public LinkList<Integer> CreateListTail(int n){
LinkList<Integer> list2=new LinkList<Integer>();
Node<Integer> node,lastNode;
lastNode=(LinkList<E>.Node<Integer>) list2.head;
for(int i=0;i<n;i++) {
int data=(int)(Math.random()*100); //生成100以内的随机数
node=new Node<Integer>(data, null);
lastNode.next=node;
lastNode=node;
list2.count++;
}
return list2;
}
}
测试代码
package LinkList;
/**
* 基本数据类型测试
*/
public class LinkListTest1 {
public static void main(String[] args) {
LinkList<Integer> nums = new LinkList<Integer>();
nums.IsEmpty();
System.out.println("——————————插入1到5,并读取内容——————————");
for (int i = 1; i <= 5; i++)
nums.ListInsert(i, 2*i);
nums.IsEmpty();
int num;
for (int i = 1; i <= 5; i++) {
num = nums.GetData(i);
System.out.println("第" + i + "个位置的值为:" + num);
}
System.out.println("——————————查找0、2、10是否在表中——————————");
System.out.print("0的位置:");
System.out.println(nums.LocateElem(0));
System.out.print("2的位置:");
System.out.println(nums.LocateElem(2));
System.out.print("10的位置:");
System.out.println(nums.LocateElem(10));
System.out.println("——————————删除2、10——————————");
num = nums.ListDelete(1);
System.out.println("已删除:" + num);
num = nums.ListDelete(4);
System.out.println("已删除:" + num);
System.out.println("当前表长:" + nums.ListLength());
for (int i = 1; i <= nums.ListLength(); i++) {
num = nums.GetData(i);
System.out.println("第" + i + "个位置的值为:" + num);
}
nums.ClearList();
nums.IsEmpty();
}
}
表为空!
——————————插入1到5,并读取内容——————————
插入成功!
插入成功!
插入成功!
插入成功!
插入成功!
表不为空!
第1个位置的值为:2
第2个位置的值为:4
第3个位置的值为:6
第4个位置的值为:8
第5个位置的值为:10
——————————查找0、2、10是否在表中——————————
0的位置:查找失败!
0
2的位置:1
10的位置:5
——————————删除2、10——————————
删除成功!
已删除:2
删除成功!
已删除:10
当前表长:3
第1个位置的值为:4
第2个位置的值为:6
第3个位置的值为:8
线性表已清空!
表为空!
package LinkList;
public class LinkListTest2 {
public static void main(String[] args) {
LinkList<Student> students =new LinkList<Student>();
students .IsEmpty();
System.out.println("——————————插入1到5,并读取内容——————————");
Student[] stus= {new Student("小A",11),new Student("小B",12),new Student("小C",13),
new Student("小D",14),new Student("小E",151)};
for(int i=1;i<=5;i++)
students.ListInsert(i, stus[i-1]);
students .IsEmpty();
Student stu;
for(int i=1;i<=5;i++) {
stu=students .GetData(i);
System.out.println("第"+i+"个位置为:"+stu.name);
}
System.out.println("——————————查找小A、小E、小龙是否在表中——————————");
System.out.print("小A的位置:");
stu=stus[0];
System.out.println(students .LocateElem(stu));
System.out.print("小E的位置:");
stu=stus[4];
System.out.println(students .LocateElem(stu));
System.out.print("小龙的位置:");
stu=new Student("小龙",11);
System.out.println(students .LocateElem(stu));
System.out.println("——————————删除小E、小B——————————");
stu=students .ListDelete(2);
System.out.println("已删除:"+stu.name);
stu=students .ListDelete(4);
System.out.println("已删除:"+stu.name);
System.out.println("当前表长:"+students .ListLength());
for(int i=1;i<=students .ListLength();i++) {
stu=students .GetData(i);
System.out.println("第"+i+"个位置为:"+stu.name);
}
students .ClearList();
students .IsEmpty();
}
}
class Student{
public Student(String name, int age) {
this.name=name;
this.age=age;
}
String name;
int age;
}
表为空!
——————————插入1到5,并读取内容——————————
插入成功!
插入成功!
插入成功!
插入成功!
插入成功!
表不为空!
第1个位置为:小A
第2个位置为:小B
第3个位置为:小C
第4个位置为:小D
第5个位置为:小E
——————————查找小A、小E、小龙是否在表中——————————
小A的位置:1
小E的位置:5
小龙的位置:查找失败!
0
——————————删除小E、小B——————————
删除成功!
已删除:小B
删除成功!
已删除:小E
当前表长:3
第1个位置为:小A
第2个位置为:小C
第3个位置为:小D
线性表已清空!
表为空!
3.11单链表结构与顺序存储结构优缺点 70
存储分配方式
顺序存储结构用一段连续的存储单元依次存储线性表的数据元素
单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素
时间性能
查找
顺序存储结构O(1)
单链表O(n)
插入和删除
顺序存储结构需要平均移动表长一半的元素,时间为O(n)
单链表在线出某位置的指针后,插入和删除时间仅为O(1)
空间性能
顺序存储结构需要预分配存储空间,分大了,浪费,分小了易发生上溢
单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制
• 若线性表需要频繁查找,很少进行插入和删除操作时,宜采用顺序存储结 构。若需要频繁插入和删除时,宜采用单链表结构。比如说游戏开发中, 对于用户注册的个人信息,除了注册时插入数据外,绝大多数情况都是读取,所以应该考虑用顺序存储结构 。而游戏中的玩家的武器或者装备列 表,随着玩家的游戏过程中,可能会随时增加或删除,此时再用顺序存储 就不大合适了,主事链表结构就可以大展拳脚。当然,这只是简单的类比, 现实中的软件开发,要考虑的问题会复杂得多。
• 当线性表中的元素个数变化较大或者根本不知道有多大时,最好用单链表结构, 这样可以不需要考虑存储空间的大小问题。而如果事先知道线性表的大致长度,比如一年 12 个月,一周就是星期一至星期日共七天,这种用 顺序存储结构效率会高很多。
3.12静态链表 71
对于一些语言,如basic、fortran等早期的编程高级语言,由于没有指针,这链表结构,按照前面我们的讲法,它就没法实现了。怎么办呢?
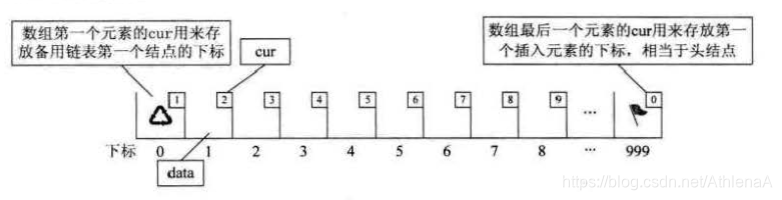
用数组描述的链表叫做静态链表(数组中的元素由两个数据域组成,data和cur)。也就是说,数组的每 个下标都对应一个data和一个 curo。数据域data,用来存放数据元素, 也就是通常我 们要处理的数据;而游标 cur 相当于单链表中的 next 指针,存放该元素的后继在数组中的下标。
数组元素由两个数据域data和cur组成:data存放数据元素;cur相当于单链表中的next指针,称为游标。
为了我们方便插入数据,我们通常会把数组建立得大一些,以便有一些空闲空间 可以便于插入时不至于溢出。
public class StaticLinkList<E> {
private SNode<E>[] nodes;
private int maxSize;
public StaticLinkList(){
this(1000);
}
public StaticLinkList(int maxSize){
//初始化的数组状态--将一维数组nodes中各个分量链接成一个备用链表
//nodes[0].cur为头指针,0表示空指针
this.maxSize=maxSize;
nodes=new SNode[this.maxSize];//泛型的数组建立似乎有些问题
for(int i=0;i<this.maxSize-1;i++) {
nodes[i]=new SNode<E>(null, i+1);
}
nodes[maxSize-1]=new SNode<E>(null, 0);//目前静态链表为空.最后一个元素的cur为0
}
class SNode<E> {
E data;
int cur;
public SNode(E data,int cur){
this.data=data;
this.cur=cur;
}
}
另外我们对数组第一个和最后一个元素作为特殊元素处理,不存数据。我们通常 把未被使用的数组元素称为备用链表。
数组中的第一个元素(下标为0)的cur存放备用链表的第一个结点的下标(即下一个元素插入存放的位置),数组的最后一个元素的cur则存放第一个有数值的元素的下标(即存放链头的位置),相当于单链表中的头结点作用,当整个链表为空时,则为 02。
此时的图示相当于初始化的数组状态,对应于StaticLinkList初始化方法
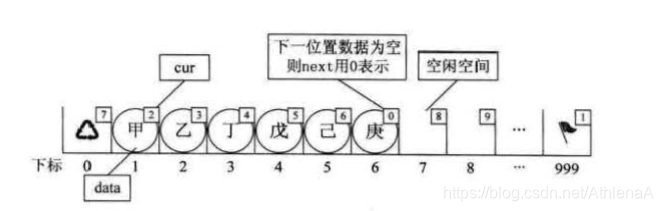
假设我们已经将数据存入静态链表,比如分别存放着"甲"、 “乙”、 “丁”、“戊”、 “己”、“庚"等数据,
此时"甲"这里就存有下一元素"乙” 的游标 2,"乙"则存有下一元素"丁"的 下标 3。
而"庚"是最后一个有值元素,所以它的 cur 设置为 0。
而最后一个元素的 cur 则因"甲"是第一有值元素而存有它的下标为 1。
而第一个元素则因空闲空间的第一个元素下标为 7 ,所以宫的 cur 存有 7。
3.12.1静态链表的插入操作 73
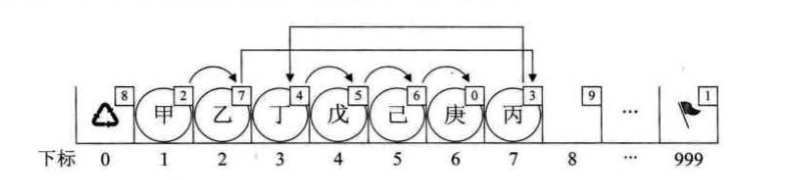
将元素”丙”插入到”乙”和”丁”之间
静态链表中要解决的是: 如何用静态模拟动态链表结构的存储空间的分配,需要 时申请, 无用时释放。
我们前面说过,在动态链表中,结点的申请和释放分别借用 malloc ()和 free() 两个函数来实现。在静态链表中,操作的是数组,不存在像动态链表的结点申请和 释放问题,所以我们需要自己实现这两个函数,才可以做插入和删除的操作。
为了辨明数组中哪些分量未被使用,解决的办法是将所有未被使用过的及已被删 除的分量用游标链成一个备用的链表, 每当进行插入时,便可以从备用链装上取得第 一个结点作为待插入的新结点。
/**
* 返回可分配结点下标
* 若备用空间链表非空,则返回分配的结点下标,否则返回0
*/
public int malloc_sll() {
int i= nodes[0].cur; //当前数组第一个元素的cur存的值,就是要返回的第一个备用 空闲的下标
nodes[0].cur=nodes[i].cur;//第i个分量要拿来用了,所以指向下一个分量
//由于要拿出一个分量来使用了,所以我们就得把它的下一个分量用来做备用
//注意,不是nodes[0].cur=nodes[0].cur+1,下一个分量不一定就是下标加一;
return i;
}
这段代码有意思,一方面它的作用就是返回一个下标值,这个值就是数组头元素 的cur存的第一个空闲的下标。从上面的图示例子来看,其实就是返回 7。
那么既然下标为 7 的分量准备要使用了,就得有接替者,所以就把分量 7 的 cur. 值赋值给头元素,也就是把 8 给 space[O].cur,之后就可以继续分配新的空闲分量, 实现类似 malloc()函数的作用。
现在我们如果需要在"乙"和"丁" 之间,插入一个值为"丙"的元素,按照以 前顺序存储结构的做法,应该要把"丁"、“戊”、“己”、"庚"这些元素都往后移一 位。 但目前不需要,因为我们有了新的手段。
新元素 “丙”,想插队是吧?可以,你先悄悄地在队伍最后一排第 7 个游标位置待 着,我一会就能帮你搞定。我接着找到了"乙",告诉他,你的 cur 不是游标为 3 的 "丁"了,这点小钱,意思意思,你把你的下一位的游标改为 7 就可以了。"乙"叹了 口气,收了钱把 cur值改了。此时再回到"丙"那里,说你把你的 cur 改为 3. 就这 样,在绝大多数人都不知道的情况下,整个排队的次序发生了改变
/**
* 插入操作,i代表第i个位置,而不是下标
* 注意插入到第一个位置的特殊性
* 在 L 中第 i 个元素之前插入新的数据元素 e
*/
public void listInsert(int i,E e) {
if(i<1||i>this.getLength()+1)
throw new RuntimeException(“插入位置错误!”);
if(getLength()==maxSize-2)
throw new RuntimeException(“表已满,无法插入!”);
int j=this.malloc_sll();//获得空闲分量的下标
nodes[j].data=e; //将数据赋值给此分量的data
int p; 第i-1个元素的下标
if(i==1) {
p=maxSize-1;//p首先是最后一个元素的下标,也就是开始第一个有值元素的位置
}else {
p=getIndex(i-1);
}
nodes[j].cur=nodes[p].cur;//设置新元素的下一个位置的游标
nodes[p].cur=j;//设置i-1位置的下一个位置的游标是新元素
}
就这样,我们实现了在数组中,实王归之移动元素,却插入了数据的操作
/**
* 获取第i个元素的下标
*/
public int getIndex(int i){
if(i<1||i>this.getLength())
throw new RuntimeException("查找位置错误!");
int k=nodes[maxSize-1].cur;
for (int j=1;j<i;j++)
k=nodes[k].cur;
return k;
}
/**
* 获取第i个元素
*/
public SNode<E> getElement(int i){
return nodes[getIndex(i)];
}
3.12.2静态链表的删除操作 75
将元素”甲”删除
和前面一样,删除元素时,原来是需要释放结点的函数 free 0。现在我们也得自 己实现它:
/**
* 删除第i个位置的结点
*/
public SNode<E> listDelete(int i) {
if(i<1||i>getLength())
throw new RuntimeException("删除位置错误!");
int m= getIndex(i);
int p; //第i-1个元素的下标
if(i==1) {
p=maxSize-1;
}else {
p=getIndex(i-1);
}
nodes[p].cur=nodes[m].cur;//特殊情况:告诉计算机现在 "甲"已经离开了,"乙"才是第一个元素。
free_sll(m);
return nodes[m];
}
/**
* 将下标为i元素回收到备用链表中
*/
public void free_sll(int i) {
nodes[i].cur=nodes[0].cur;//把第一个元素cur值赋值给要是删除的分量cur
nodes[0].cur=i;//把要删除的分量下标赋值给第一个元素的cur
}
意思就是"甲"现在要走,这个位置就空出来了,也就是,未来如果有新人来, 最优先考虑这里,所以原来的第一个空位分量,即下标是 8 的分量,它降级了,把 8 给" 甲"所在下标为 1 的分量的 cur ,也就是 space[l].cur=space[O].cur=8
而 space[O].cur=k=l 其实就是让这个删除的位置成为第一个优先空位,把它存人第一个元素的 cur 中
/**
* 返回静态链表的长度
*/
public int getLength() {
int length=0;
int i=nodes[maxSize-1].cur;
while(i!=0) {
i=nodes[i].cur;
length++;
}
return length;
}
静态链表代码
package StaticLinkList;
/**
* 说明:
* 1.数组第一个元素的cur为备用链表第一个结点下标,
* 数组最后一个元素的cur为第一个有数据的元素的下标,相当于头结点
* 最后一个有值元素的 cur为0
* 2.插入删除操作时,获取第i-1个元素的 下标时,应注意i-1=0的情况
* 3.注释中的“位置”指的是在链表中的位置,“下标”代表数组中的下标,勿搞混
* 4.程序关键:获取下标,在数组层面上操作
* 5.程序中主要写了插入删除操作,其余基本操作与之前文章类似
*
* 问题:
* 1.泛型数组的建立
* 2.书中P73的if(space[0].cur)和P74的if(j)是属于判断什么?
*
* @author Yongh
*/
public class StaticLinkList<E> {
private SNode<E>[] nodes;
private int maxSize;
public StaticLinkList(){
this(1000);
}
public StaticLinkList(int maxSize){
this.maxSize=maxSize;
nodes=new SNode[this.maxSize];//泛型的数组建立似乎有些问题
for(int i=0;i<this.maxSize-1;i++) {
nodes[i]=new SNode<E>(null, i+1);
}
nodes[maxSize-1]=new SNode<E>(null, 0);
}
class SNode<E> {
E data;
int cur;
public SNode(E data,int cur){
this.data=data;
this.cur=cur;
}
}
/**
* 获取第i个元素的下标
*/
public int getIndex(int i){
if(i<1||i>this.getLength())
throw new RuntimeException("查找位置错误!");
int k=nodes[maxSize-1].cur;
for (int j=1;j<i;j++)
k=nodes[k].cur;
return k;
}
/**
* 获取第i个元素
*/
public SNode<E> getElement(int i){
return nodes[getIndex(i)];
}
/**
* 返回可分配结点下标
*/
public int malloc_sll() {
int i= nodes[0].cur;
nodes[0].cur=nodes[i].cur;//第i个分量要拿来用了,所以指向下一个分量
//注意,不是nodes[0].cur=nodes[0].cur+1,下一个分量不一定就是下标加一;
return i;
}
/**
* 插入操作,i代表第i个位置,而不是下标
* 注意插入到第一个位置的特殊性
*/
public void listInsert(int i,E e) {
if(i<1||i>this.getLength()+1)
throw new RuntimeException("插入位置错误!");
if(getLength()==maxSize-2)
throw new RuntimeException("表已满,无法插入!");
int j=this.malloc_sll();
nodes[j].data=e;
int p; 第i-1个元素的下标
if(i==1) {
p=maxSize-1;
}else {
p=getIndex(i-1);
}
nodes[j].cur=nodes[p].cur;
nodes[p].cur=j;
}
/**
* 删除第i个位置的结点
*/
public SNode<E> listDelete(int i) {
if(i<1||i>getLength())
throw new RuntimeException("删除位置错误!");
int m= getIndex(i);
int p; //第i-1个元素的下标
if(i==1) {
p=maxSize-1;
}else {
p=getIndex(i-1);
}
nodes[p].cur=nodes[m].cur;
free_sll(m);
return nodes[m];
}
/**
* 将下标为i元素回收到备用链表中
*/
public void free_sll(int i) {
nodes[i].cur=nodes[0].cur;
nodes[0].cur=i;
}
/**
* 返回静态链表的长度
*/
public int getLength() {
int length=0;
int i=nodes[maxSize-1].cur;
while(i!=0) {
i=nodes[i].cur;
length++;
}
return length;
}
}
测试代码
package StaticLinkList;
public class StaticLinkListTest {
public static void main(String[] args) {
StaticLinkList<Student> students =new StaticLinkList<Student>();
System.out.println("——————————插入1到5,并读取内容——————————");
Student[] stus= {new Student("小A",11),new Student("小B",12),new Student("小C",13),
new Student("小D",14),new Student("小E",151)};
for(int i=1;i<=5;i++)
students.listInsert(i, stus[i-1]);
System.out.println("表长:"+students .getLength());
Student stu;
for(int i=1;i<=5;i++) {
stu=students .getElement(i).data;
System.out.println("第"+i+"个位置为:"+stu.name);
}
System.out.println("——————————删除小B、小E——————————");
stu=students .listDelete(2).data;
System.out.println("已删除:"+stu.name);
stu=students .listDelete(4).data;
System.out.println("已删除:"+stu.name);
System.out.println("当前表长:"+students .getLength());
for(int i=1;i<=students .getLength();i++) {
stu=students .getElement(i).data;
System.out.println("第"+i+"个位置为:"+stu.name);
}
System.out.println("表长:"+students.getLength());
}
}
class Student{
public Student(String name, int age) {
this.name=name;
this.age=age;
}
String name;
int age;
}
——————————插入1到5,并读取内容——————————
表长:5
第1个位置为:小A
第2个位置为:小B
第3个位置为:小C
第4个位置为:小D
第5个位置为:小E
——————————删除小B、小E——————————
已删除:小B
已删除:小E
当前表长:3
第1个位置为:小A
第2个位置为:小C
第3个位置为:小D
表长:3
3.12.3静态链表优缺点 77
优点
在插入和删除操作时,只需要修改游标,不需要移动元素,从而改进了在顺序存储结构中的插入和删除操作需要移动大量元素的缺点
缺点
没有解决连续存储分配带来的表长难以确定的问题
失去了顺序存储结构随机存储的特性
总的来说,静态链表其实是为了给没有指针的高级语言设计的一种实现单链袭能 力的方法。尽管大家不一定会用得上,但这样的思考方式是非常巧妙的,应该理解其 思想,以备不时之需。
3.13循环链表 78
这个轮回的思想很有意思。它强调了不管你今生是穷是富,如果持续行善积德,下辈子就会好过,反之就会遭到报应。
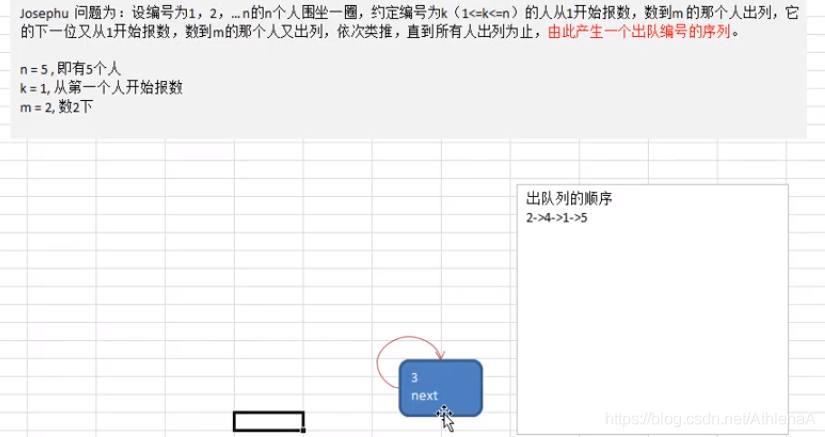
Josephu(约瑟夫、约瑟夫环) 问题
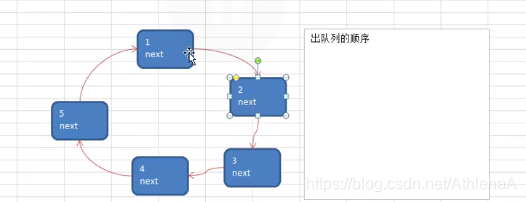
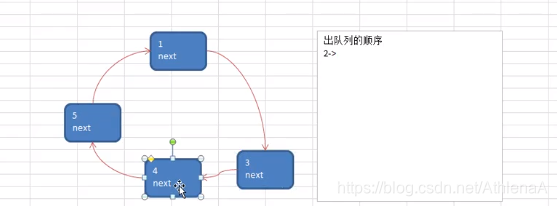
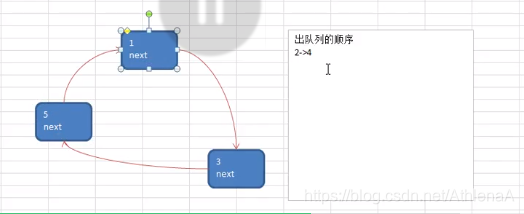
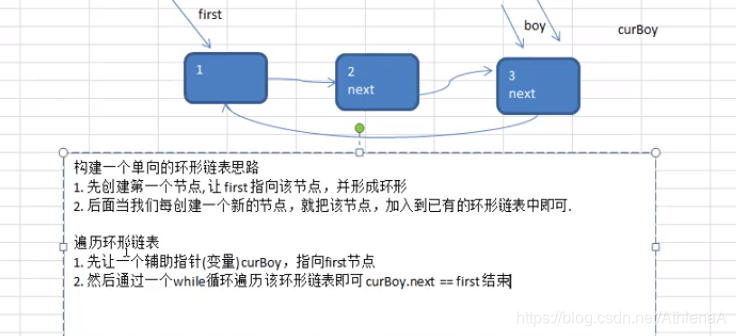
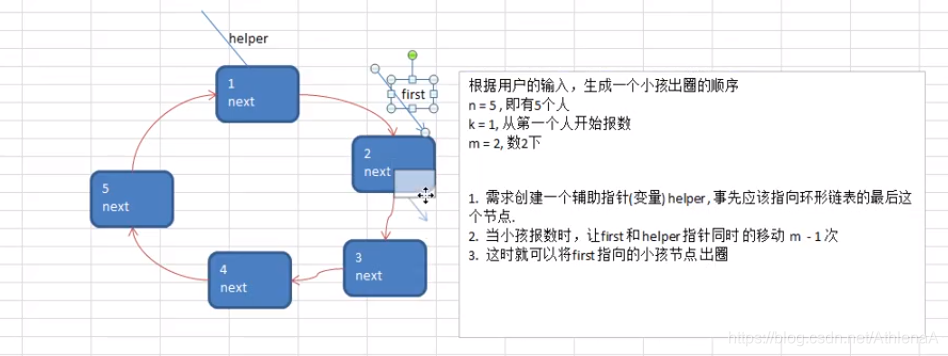
Josephu 问题为:设编号为1,2,… n的n个人围坐一圈,约定编号为k(1<=k<=n)的人从1开始报数,数到m 的那个人出列,它的下一位又从1开始报数,数到m的那个人又出列,依次类推,直到所有人出列为止,由此产生一个出队编号的序列。
提示:用一个不带头结点的循环链表来处理Josephu 问题:先构成一个有n个结点的单循环链表,然后由k结点起从1开始计数,计到m时,对应结点从链表中删除,然后再从被删除结点的下一个结点又从1开始计数,直到最后一个结点从链表中删除算法结束。
移动一下,是数了两位
package com.zcr.linkedlist;
/**
* @author zcr
* @date 2019/7/5-18:25
*/
public class SingleCircleLinkedListDemo {
public static void main(String[] args) {
//创建环形链表
SingleCircleLinkedList circleLinkedList = new SingleCircleLinkedList();
circleLinkedList.addBoy(125);//加入五个小孩节点
circleLinkedList.showBoy();
//测试小孩出圈问题---约瑟夫问题
circleLinkedList.countBoy(10,20,125);//2 4 1 5 3
}
}
//创建一个Boy类,表示一个节点
class Boy {
private int no;//编号
private Boy next;//指向下一个节点,初始为空
public Boy(int no) {
this.no = no;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public Boy getNext() {
return next;
}
public void setNext(Boy next) {
this.next = next;
}
}
//创建单向环形链表
class SingleCircleLinkedList {
//创建一个first节点
private Boy first = null;
//添加小孩节点,构建环形链表
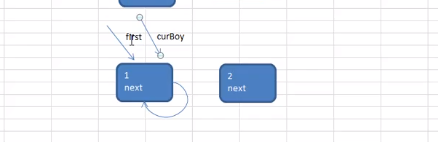
public void addBoy(int nums) {
//nums做校验
if (nums < 2) {
System.out.println("nums的值不正确");
return;
}
//辅助变量,帮助构建环形链表
Boy curBoy = null;
//使用for循环来创建环形链表
for (int i = 1; i <= nums; i++) {
//根据编号创建小孩节点
Boy boy = new Boy(i);
//如果是第一个小孩
if (i == 1) {
first = boy;
first.setNext(first);//构成一个环,只是这个环里只有一个小孩
curBoy = first;//让curBoy指向第一个小孩
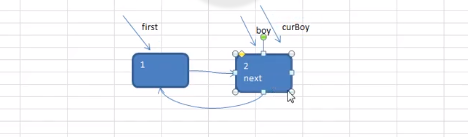
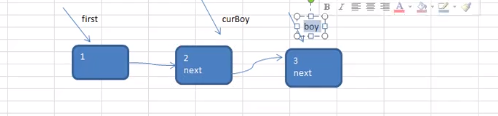
} else {
curBoy.setNext(boy);
boy.setNext(first);
curBoy = boy;
}
}
}
//遍历单向循环链表
public void showBoy() {
//判断链表是否为空
if (first == null){
System.out.println("链表为空");
return;
}
//因为first不能动,因此我们仍然使用一个辅助指针完成遍历
Boy curBoy = first;
while (true){
System.out.printf("小孩的编号%d\n",curBoy.getNo());
if (curBoy.getNext() == first) {//说明遍历完毕
break;
}
curBoy = curBoy.getNext();//curBoy后移
}
}
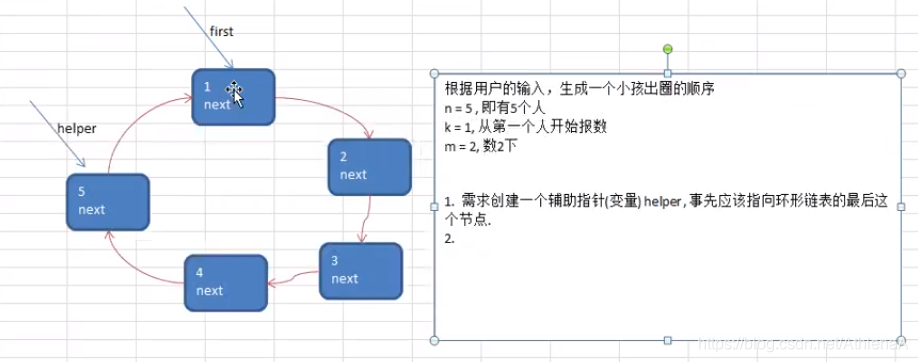
//根据用户的输入,计算出小孩出圈的顺序
/**
*
* @param startNo 表示从第几个小孩开始数数
* @param countNum 表示数几下
* @param nums 表示最初有多少个小孩在圈中
*/
public void countBoy(int startNo,int countNum,int nums) {
//先对数据做校验
if (first == null || startNo < 1 || startNo > nums) {
System.out.println("参数输入有误,请重新输入");
return;
}
//创建辅助变量,帮助完成小孩出圈
Boy helper = first;
while (true) {
if (helper.getNext() == first) {//说明helper指向最后的小孩节点
break;
}
helper = helper.getNext();
}
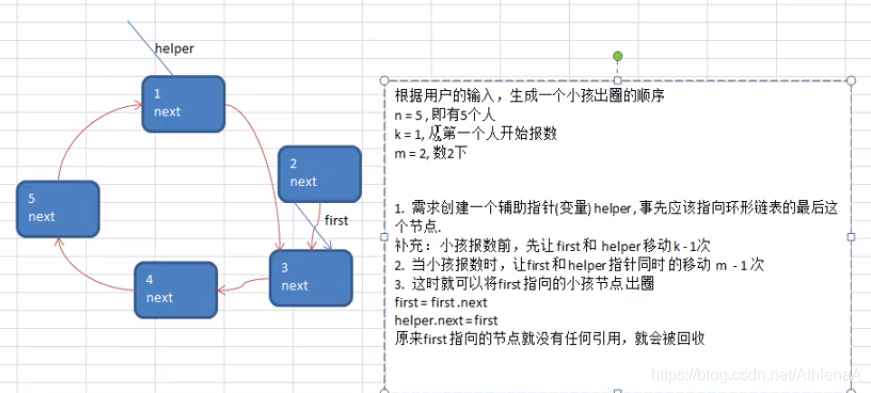
//小孩报数前,先让first和helper移动k-1次
for (int i = 0; i < startNo - 1; i++) {
first = first.getNext();
helper = helper.getNext();
}
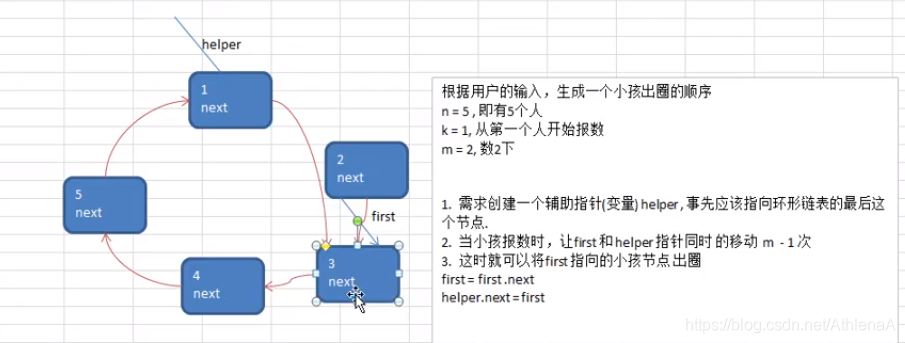
//当小孩报数时,让first和helper指针同时的移动m-1次,然后出圈
//这里是一个循环操作,直到圈中只有一个节点
while (true) {
if (helper == first) {//说明圈中只有一个节点了
break;
}
//让first和helper指针同时的移动countNum - 1
for (int i = 0; i < countNum - 1; i++) {
first = first.getNext();
helper = helper.getNext();
}
//这时first指向的节点,就是要除权的小孩节点
System.out.printf("小孩%d出圈\n",first.getNo());
//这时将first指向的小孩出圈
first = first.getNext();
helper.setNext(first);
}
System.out.printf("最后留在圈中的小孩编号为%d\n",first.getNo());
}
}
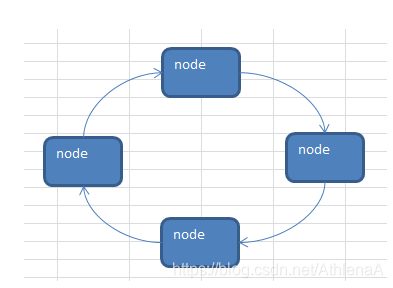
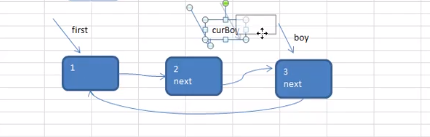
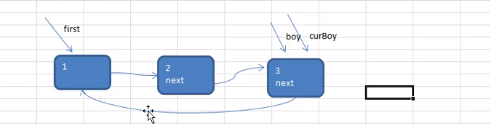
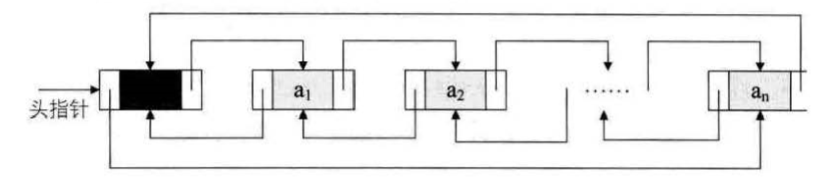
将单链表中终端结点的指针端由空指针改为指向头指针,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表。 (circular linked list) 。
循环链表解决了一个很麻烦的问题。 如何从当中一 个结点出发,访问到链表的全部结点。
为了使空链表与非空链表处理一致,我们通常设一个头结点,当然 , 这并不是 说,循环链表一定要头结点,这需要注意。
循环链表带有头结点的空链表:
对于非空的循环链表:
其实循环链袭和单链表的主要差异就在于循环的判断条件土,原沫是判断 p->next 是否为空,现在则是 p -> next 不等于头结点,则循环未结束。
在单链表中,我们有了头结点时,我们可以用 0(1)的时间访问第一个结点,但对 于要访问到最后一个结点,却需要 O(n)时间,因为我们需要将单链表全部扫描一遍。
有没有可能用 0(1)的时间由链表指针访问到最后一个结点呢?当然可以。
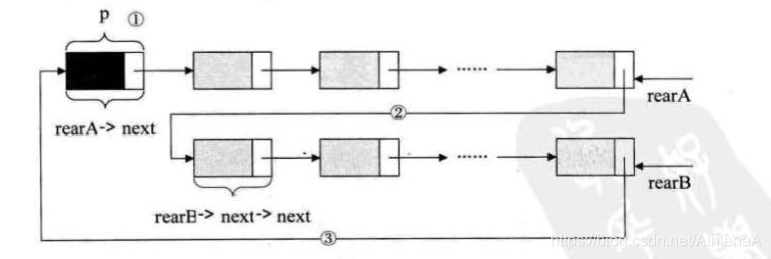
不过我们需要改造一下这个循环链粟,不用头指针,而是用指向终端结点的尾指针来表示循环链表(如图 3.13.5 所示) ,此时查找开始结点和终端结点都很方便了。
从上圈中可以看到,终端结点用尾指针 rear 指示,则查找终端结点是 0(1) ,而开 始结点,其实就是 rear->neJæ->next,其时间复杂也为 0(1)。
举个程序的例子,要将两个循环链袭合并成一个表时,有了尾指针就非常简单 了。 比如下面的这两个循环链衰,它们的尾指针分别是 rearA 和 rearB
要想把它们合井,只需要如下的操作即可
Node p=rearA.next;
rearA.next=rearB.next.next;
Node q=rearB.next;
rearB.next=p;
q=null;
3.14双向链表 81
就像每个人的人生一样,欲收获就得付代价。双向链表既然是比单链表多了如可以反向遍历查找等的数据结构,那么也就需要付出一些小的代价。
使用带head头的双向链表实现 –水浒英雄排行榜
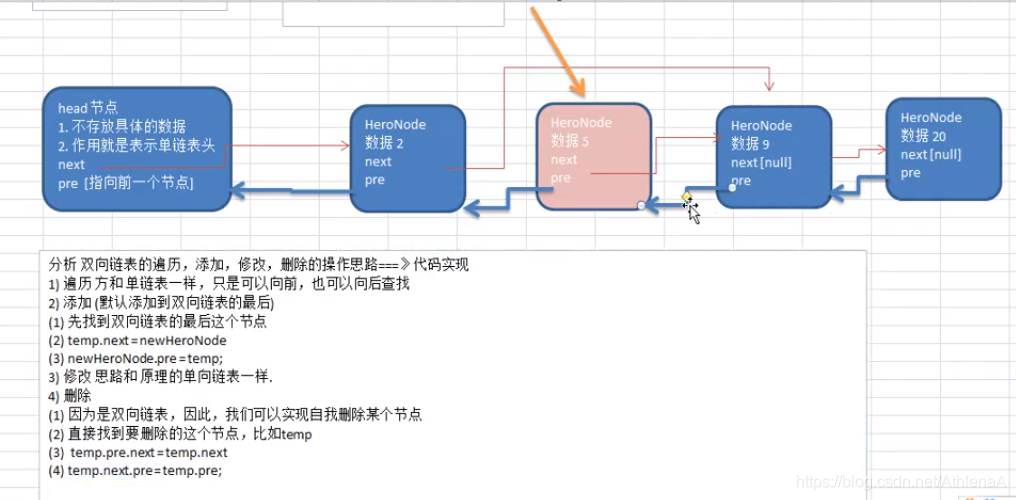
管理单向链表的缺点分析:
单向链表,查找的方向只能是一个方向,而双向链表可以向前或者向后查找。
单向链表不能自我删除,需要靠辅助节点 ,而双向链表,则可以自我删除,所以前面我们单链表删除时节点,总是找到temp,temp是待删除节点的前一个节点(认真体会).
示意图帮助理解删除
package com.zcr.linkedlist;
/**
* @author zcr
* @date 2019/7/5-17:37
*/
public class DoubleLinkedListDemo {
public static void main(String[] args) {
System.out.println("双向链表测试:");
//先创建几个节点
HeroNode2 hero1 = new HeroNode2(1,"宋江","及时雨 ");
HeroNode2 hero2 = new HeroNode2(2,"卢俊义","玉麒麟");
HeroNode2 hero3 = new HeroNode2(3,"吴用","智多星");
HeroNode2 hero4 = new HeroNode2(4,"林冲","豹子头");
//创建双向链表
DoubleLinkedList doubleLinkedList = new DoubleLinkedList();
/*doubleLinkedList.add(hero1);
doubleLinkedList.add(hero2);
doubleLinkedList.add(hero3);
doubleLinkedList.add(hero4);
doubleLinkedList.list();*/
//按照编号添加
doubleLinkedList.addByOrder(hero3);
doubleLinkedList.addByOrder(hero1);
doubleLinkedList.addByOrder(hero2);
doubleLinkedList.list();
//修改
HeroNode2 hero5 = new HeroNode2(4,"公孙胜","入云龙");
doubleLinkedList.update(hero5);
System.out.println("修改后的链表:");
doubleLinkedList.list();
//删除
doubleLinkedList.delete(3);
System.out.println("删除后的链表:");
doubleLinkedList.list();
}
}
//定义HeroNode,每个HeroNode对象就是一个节点
class HeroNode2 {
public int no;
public String name;
public String nickname;
public HeroNode2 next;//指向下一个节点,初始值为null
public HeroNode2 pre;//指向前一个节点,初始值为null
//构造器
public HeroNode2(int no,String name,String nickname) {
this.no = no;
this.name = name;
this.nickname = nickname;
}
//为了显示方便,重写toString
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
", nickname='" + nickname + '\'' +
//", next=" + next +这个nect域不要打印了,否则每次一连串都会打印出来
'}';
}
}
//创建一个双向列表的类
class DoubleLinkedList {
//初始化
//先初始化一个头结点,头结点不要动,不存放具体的数据
private HeroNode2 head = new HeroNode2(0,"","");
//返回头结点
public HeroNode2 getHead() {
return head;
}
//遍历双向链表
//显示链表,通过遍历
public void list() {
//判断链表是否为空
if(head.next == null) {
System.out.println("链表为空");
return;
}
//因为头结点不能动,因此我们需要一个辅助变量来遍历
HeroNode2 temp = head.next;
while(true){
//判断是否到链表最后
if (temp == null){
break;
}
//输出节点信息
System.out.println(temp);
//将temp后移
temp = temp.next;
}
}
//添加(默认添加到双向链表的最后面)
//思路,当不考虑编号顺序时,找到最后一个节点,把它的next域指向新的节点
public void add(HeroNode2 heroNode) {
//因为head节点不能动,因此我们需要一个辅助变量temp
HeroNode2 temp = head;
/*while (temp != null){
temp = temp.next;
}
temp.next = heroNode;*/
while (true) {
//找到链表的最后
if (temp.next == null){
break;
}
//如果没有找到最后,将temp后移
temp = temp.next;
}
//当退出while循环时,temp就指向了链表的最后
temp.next = heroNode;//第一次用的时候发生了空指针异常,因为我用了空对象去调用方法和属性
heroNode.pre = temp;//形成一个双向链表
}
//第二种方式在添加英雄时,根据排名将英雄插入到指定位置
//如果有这个排名,则添加失败,并给出提示
//就可以在内存中把顺序排好,比数据库中肯定要快
//因为头结点不能动,因此我们仍然通过一个辅助变量来帮助找到添加位置
//因此我们找的temp是位于添加位置的前一个节点,否则插入不了
//说明我们在比较时,是temp.next.no和需要插入的节点的no做比较
public void addByOrder(HeroNode2 heroNode) {
HeroNode2 temp = head;
boolean flag = false;//标识添加的编号是否存在,默认为false
while (true) {
if (temp.next == null){//说明temp已经在链表的最后
break;
}
if (temp.next.no > heroNode.no) {//位置找到,就在temo的后面插入
break;
} else if (temp.next.no == heroNode.no) {//说明希望添加的heroNode的编号已经存在了
flag = true;
break;
}
temp =temp.next;//后移,遍历当前的链表
}
if (flag) {//不能添加,说明编号存在
System.out.printf("准备插入的英雄的编号%d已经存在,不能加入\n",heroNode.no);
} else {
//插入到链表中,temp的后边
heroNode.pre = temp;
heroNode.next = temp.next;
if (temp.next != null) {
temp.next.pre = heroNode;
}
temp.next = heroNode;
}
}
//完成修改节点的信息,根据编号来修改,即编号不能改
public void update(HeroNode2 newHeroNode) {
//判断链表是否为空
if (head.next == null){
System.out.println("链表为空");
return;
}
//找到需要修改的节点,根据编号找
//先定义一个辅助变量
HeroNode2 temp = head.next;
boolean flag = false;//是否找到该节点
while (true) {
if (temp == null){
break;//到链表的最后的下一个节点了,已经遍历结束了
}
if (temp.no == newHeroNode.no) {//找到了
flag = true;
break;
}
temp = temp.next;
}
//根据flag判断是否找到要修改的节点
if (flag) {
temp.name = newHeroNode.name;
temp.nickname =newHeroNode.nickname;
} else {//没有找到
System.out.printf("没有找到编号为%d的节点,不能修改\n",newHeroNode.no);
}
}
//从双向链表中删除一个节点
//不需要找要删除的节点的前一个节点,可以直接找到要删除的这个节点,找到了后自我删除即可
public void delete(int no) {
//判断当前链表是否为空
if (head.next == null) {
System.out.println("链表为空,无法删除");
}
//辅助变量
HeroNode2 temp = head.next;
boolean flag = false;//是否找到待删除节点的前一个节点
while (true) {
if (temp == null) {//已经到了链表的最后一个节点
break;
}
if (temp.no == no){
flag = true;//找到了待删除节点
break;
}
temp = temp.next;
}
if (flag) {
temp.pre.next = temp.next;
//这里我们的代码有问题,以为如果要删除的节点是最后一个节点时
//如果是最后一个节点,就不需要执行下面这句话,否则会出现空指针异常
if (temp.next != null) {
temp.next.pre = temp.pre;
}
} else {
System.out.printf("要删除的节点%d不存在\n",no);
}
}
}
双向链表是在单链表的每个结点中,再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域, 一个指向直接后继,另一个指向直接前驱。
package DuLinkList;
public class DuLinkList<E> {
private Node<E> head;
private int count;
/**
* 结点
*/
class Node<E> {
E data;
Node<E> prior;
Node<E> next;
public Node(E data, Node<E> prior, Node<E> next) {
this.data = data;
this.prior = prior;
this.next = next;
}
}
/**
* 线性表的初始化
*/
public DuLinkList() {
head = new Node<E>(null, null, null);
head.prior = head.next = head;
count = 0;
}
既然单链表也可以有循环链衰,那么双向链表当然也可以是循环表。
双向链表的循环带头结点的空链表
非空的循环的带头结点的双向链表如下图所示
由于这是双向链表,那么对于链表中的某一个结点 p,它的后继的前驱是谁?当 然还是它自己。它的前驱的后继自然也是Z 自己,即:
p->next->prior = p = p- >prior- >next
双向链表是单链表中扩展出来的结构,所以宫的很多操作是和单链裴相同的,比 如求长度的 ListLength ,查找元素的 GetElem,较得元素位置的 LocateElem 等,这些 操作都只要涉及一个方向的指针即可,另一指针多了也不能提供什么帮助。
双向链表既然是比单链 表多了如可以反向遍历查找等数据结构,那么也就需要付出一些小的代价:在插入和 删除时,需要更改两个指针变景。
双向链表在插入和删除时,需要更改两个指针变量
我们现在假设存储元素 e 的结点为s,要实现将结点 s 插入到结点 p 和 p -> next 之间需要下面几步
s->prior = p;
s->next = p->next;
p->next->prior = s;
p->next = s;
顺序是先搞定 s 的前驱和后继,再搞定后结点的前驱,最 后解决前结点的后继。
删除结点p,只需要下面两步骤
p->prior->next = p->next;
p->next->prior = p->prior;
free§;
好了,简单总结一下,双向链衰相对于单链表来说,要更复杂一些,毕竟官多了 prior 指针,对于插入和删除时,需要格外小心。另外它由于每个结点都需要记录两份 指针,所以在空间上是要占用略多一些的。不过,由于它良好的对称性,使得对某个 结点的前后结点的操作,带来了方便,可以有效提高算法的时间性能。说白了,就是 用空间来换时间。
双向链表代码
package DuLinkList;
public class DuLinkList<E> {
private Node<E> head;
private int count;
/**
* 结点
*/
class Node<E> {
E data;
Node<E> prior;
Node<E> next;
public Node(E data, Node<E> prior, Node<E> next) {
this.data = data;
this.prior = prior;
this.next = next;
}
}
/**
* 线性表的初始化
*/
public DuLinkList() {
head = new Node<E>(null, null, null);
head.prior = head.next = head;
count = 0;
}
/**
* 获取第i个元素
*/
public Node<E> getElement(int i) {
if (count == 0)
throw new RuntimeException("空表,无法查找!");
if (i < 1 || i > count)
throw new RuntimeException("查找位置错误!");
Node<E> node = head.next;
for (int j = 1; j < i; j++) {
node = node.next;
}
return node;
}
/**
* 在第i个位置插入元素
*/
public void listInsert(int i, E data) {
if (i < 1 || i > count + 1)
throw new RuntimeException("插入位置错误!");
Node<E> node = new Node<E>(data, null, null);
if (i == 1) {
node.next = head.next;
node.prior = head;
head.next.prior = node;
head.next = node;
} else {
Node<E> pNode = getElement(i - 1);
node.next = pNode.next;
node.prior = pNode;
pNode.next.prior = node;
pNode.next = node;
}
count++;
}
/**
* 删除第i个元素
*/
public E listDelete(int i) {
if (i < 1 || i > count)
throw new RuntimeException("删除位置错误!");
Node<E> node = getElement(i);
E e = node.data;
if (i == 1) {
head.next = node.next;
node.next.prior = node.prior;
node = null;
} else {
node.next.prior = node.prior;
node.prior.next = node.next;
node = null;
}
count--;
return e;
}
public int listLength() {
return count;
}
}
测试代码
package DuLinkList;
public class DuLinkListTest {
public static void main(String[] args) {
DuLinkList<Student> students = new DuLinkList<Student>();
System.out.println("——————————插入1到5,并读取内容——————————");
Student[] stus = { new Student("小A", 11), new Student("小B", 12), new Student("小C", 13), new Student("小D", 14),
new Student("小E", 151) };
for (int i = 1; i <= 5; i++)
students.listInsert(i, stus[i - 1]);
System.out.println("表长:" + students.listLength());
Student stu;
for (int i = 1; i <= 5; i++) {
stu = students.getElement(i).data;
System.out.println("第" + i + "个位置为:" + stu.name);
}
System.out.println("——————————删除小A、小E——————————");
stu = students.listDelete(1);
System.out.println("已删除:" + stu.name);
stu = students.listDelete(4);
System.out.println("已删除:" + stu.name);
System.out.println("当前表长:" + students.listLength());
for (int i = 1; i <= students.listLength(); i++) {
stu = students.getElement(i).data;
System.out.println("第" + i + "个位置为:" + stu.name);
}
}
}
class Student {
public Student(String name, int age) {
this.name = name;
this.age = age;
}
String name;
int age;
}
——————————插入1到5,并读取内容——————————
表长:5
第1个位置为:小A
第2个位置为:小B
第3个位置为:小C
第4个位置为:小D
第5个位置为:小E
——————————删除小A、小E——————————
已删除:小A
已删除:小E
当前表长:3
第1个位置为:小B
第2个位置为:小C
第3个位置为:小D
在阅读过他人的博客后,发现自己的查找方法没有利用好双链表的特性,重写查找方法如下:
/**
* 获取第i个元素
*/
public Node<E> getElement(int i) {
if (count == 0)
throw new RuntimeException("空表,无法查找!");
if (i < 1 || i > count)
throw new RuntimeException("查找位置错误!");
if (i <= count / 2) { // 正向查找
Node<E> node = head.next;
for (int j = 1; j < i; j++) {
node = node.next;
}
return node;
} else { // 反向查找
Node<E> node = head.prior;
int k = count - i;
for (int j = 0; j < k; j++) {
node = node.prior;
}
return node;
}
}
另一份
/**
* Java 实现的双向链表。
* 注:java自带的集合包中有实现双向链表,路径是:java.util.LinkedList
*
* @author skywang
* @date 2013/11/07
*/
public class DoubleLink<T> {
// 表头
private DNode<T> mHead;
// 节点个数
private int mCount;
// 双向链表“节点”对应的结构体
private class DNode<T> {
public DNode prev;
public DNode next;
public T value;
public DNode(T value, DNode prev, DNode next) {
this.value = value;
this.prev = prev;
this.next = next;
}
}
// 构造函数
public DoubleLink() {
// 创建“表头”。注意:表头没有存储数据!
mHead = new DNode<T>(null, null, null);
mHead.prev = mHead.next = mHead;
// 初始化“节点个数”为0
mCount = 0;
}
// 返回节点数目
public int size() {
return mCount;
}
// 返回链表是否为空
public boolean isEmpty() {
return mCount==0;
}
// 获取第index位置的节点
private DNode<T> getNode(int index) {
if (index<0 || index>=mCount)
throw new IndexOutOfBoundsException();
// 正向查找
if (index <= mCount/2) {
DNode<T> node = mHead.next;
for (int i=0; i<index; i++)
node = node.next;
return node;
}
// 反向查找
DNode<T> rnode = mHead.prev;
int rindex = mCount - index -1;
for (int j=0; j<rindex; j++)
rnode = rnode.prev;
return rnode;
}
// 获取第index位置的节点的值
public T get(int index) {
return getNode(index).value;
}
// 获取第1个节点的值
public T getFirst() {
return getNode(0).value;
}
// 获取最后一个节点的值
public T getLast() {
return getNode(mCount-1).value;
}
// 将节点插入到第index位置之前
public void insert(int index, T t) {
if (index==0) {
DNode<T> node = new DNode<T>(t, mHead, mHead.next);
mHead.next.prev = node;
mHead.next = node;
mCount++;
return ;
}
DNode<T> inode = getNode(index);
DNode<T> tnode = new DNode<T>(t, inode.prev, inode);
inode.prev.next = tnode;
inode.next = tnode;
mCount++;
return ;
}
// 将节点插入第一个节点处。
public void insertFirst(T t) {
insert(0, t);
}
// 将节点追加到链表的末尾
public void appendLast(T t) {
DNode<T> node = new DNode<T>(t, mHead.prev, mHead);
mHead.prev.next = node;
mHead.prev = node;
mCount++;
}
// 删除index位置的节点
public void del(int index) {
DNode<T> inode = getNode(index);
inode.prev.next = inode.next;
inode.next.prev = inode.prev;
inode = null;
mCount--;
}
// 删除第一个节点
public void deleteFirst() {
del(0);
}
// 删除最后一个节点
public void deleteLast() {
del(mCount-1);
}
}
测试
/**
* Java 实现的双向链表。
* 注:java自带的集合包中有实现双向链表,路径是:java.util.LinkedList
*
* @author skywang
* @date 2013/11/07
*/
public class DlinkTest {
// 双向链表操作int数据
private static void int_test() {
int[] iarr = {10, 20, 30, 40};
System.out.println("\n----int_test----");
// 创建双向链表
DoubleLink<Integer> dlink = new DoubleLink<Integer>();
dlink.insert(0, 20); // 将 20 插入到第一个位置
dlink.appendLast(10); // 将 10 追加到链表末尾
dlink.insertFirst(30); // 将 30 插入到第一个位置
// 双向链表是否为空
System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
// 双向链表的大小
System.out.printf("size()=%d\n", dlink.size());
// 打印出全部的节点
for (int i=0; i<dlink.size(); i++)
System.out.println("dlink("+i+")="+ dlink.get(i));
}
private static void string_test() {
String[] sarr = {"ten", "twenty", "thirty", "forty"};
System.out.println("\n----string_test----");
// 创建双向链表
DoubleLink<String> dlink = new DoubleLink<String>();
dlink.insert(0, sarr[1]); // 将 sarr中第2个元素 插入到第一个位置
dlink.appendLast(sarr[0]); // 将 sarr中第1个元素 追加到链表末尾
dlink.insertFirst(sarr[2]); // 将 sarr中第3个元素 插入到第一个位置
// 双向链表是否为空
System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
// 双向链表的大小
System.out.printf("size()=%d\n", dlink.size());
// 打印出全部的节点
for (int i=0; i<dlink.size(); i++)
System.out.println("dlink("+i+")="+ dlink.get(i));
}
// 内部类
private static class Student {
private int id;
private String name;
public Student(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "["+id+", "+name+"]";
}
}
private static Student[] students = new Student[]{
new Student(10, "sky"),
new Student(20, "jody"),
new Student(30, "vic"),
new Student(40, "dan"),
};
private static void object_test() {
System.out.println("\n----object_test----");
// 创建双向链表
DoubleLink<Student> dlink = new DoubleLink<Student>();
dlink.insert(0, students[1]); // 将 students中第2个元素 插入到第一个位置
dlink.appendLast(students[0]); // 将 students中第1个元素 追加到链表末尾
dlink.insertFirst(students[2]); // 将 students中第3个元素 插入到第一个位置
// 双向链表是否为空
System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
// 双向链表的大小
System.out.printf("size()=%d\n", dlink.size());
// 打印出全部的节点
for (int i=0; i<dlink.size(); i++) {
System.out.println("dlink("+i+")="+ dlink.get(i));
}
}
public static void main(String[] args) {
int_test(); // 演示向双向链表操作“int数据”。
string_test(); // 演示向双向链表操作“字符串数据”。
object_test(); // 演示向双向链表操作“对象”。
}
}
----int_test----
isEmpty()=false
size()=3
dlink(0)=30
dlink(1)=20
dlink(2)=10
----string_test----
isEmpty()=false
size()=3
dlink(0)=thirty
dlink(1)=twenty
dlink(2)=ten
----object_test----
isEmpty()=false
size()=3
dlink(0)=[30, vic]
dlink(1)=[20, jody]
dlink(2)=[10, sky]
3.15总结回顾 84
这一章,我们主要讲的是线性衰。
先它的定义,线性表是零个或多个具有相同类型的数据元素的有限序列。然 后谈了线性表的抽象数据类型,如它的一些基本操作。
之后我们就线性表的两大结构做了讲述,先讲的是比较容易的顺序存储结构,指 的是用一段地址连续的存储单元依次存储线性表的数据元素。通常我们都是用数组来 实现这一结构。
后来是我们的重点,由顺序存储结构的插入和删除操作不方便,引出了链式存储 结构。它具有不受固定的存储空间限制,可以比较快捷的插入和删除操作的特点。
然 后我们分别就链式存储结构的不同形式,如单链表、循环链表和双向链袤做了讲解, 另外我们还讲了若不使用指针如何处理链裴结构的静态链表方法。
总的来说,线性表的这两种结构(如图 3-15-1 所示)其实是后面其他数据结构的 基础,把它们学明白了,对后面的学习有着至关重要的作用。
3.16结尾语 85
如果你觉得上学读书是受罪,假设你可以活到80岁,其实你最多也就吃了20年苦。用人生四分之一的时间来换取其余时间的幸福生活,这点苦不算啥。
第4章栈与队列 87
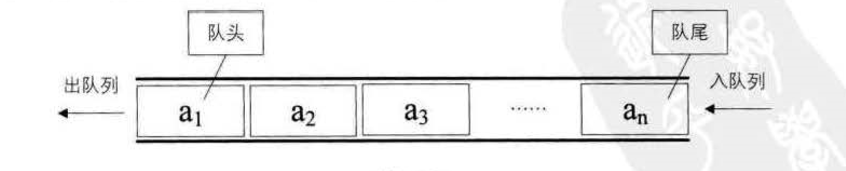
找与队列:
栈是限定仅在表尾进行插入和删除操作的线性表。 队到是只允许在一端进行插入操作、 而在另一端进行删除操作的线性表。
4.1开场白 88
想想看,在你准备用枪的时候,突然这手枪明明有子弹却打不出来,这不是要命吗。
4.2栈的定义 89
类似的很多软件,比如word、photoshop等,都有撤消(undo)的操作,也是用栈这种思想方式来实现的。
请输入一个表达式
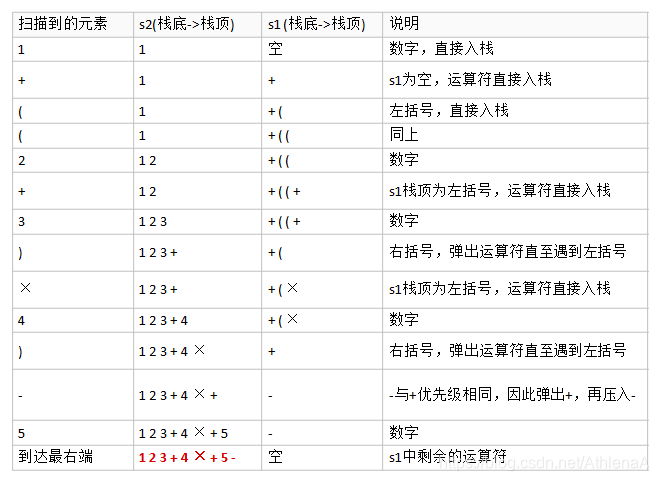
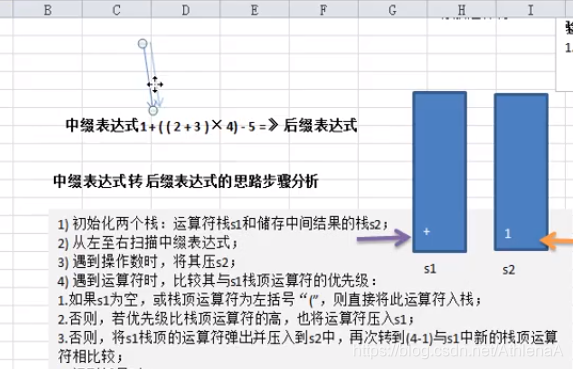
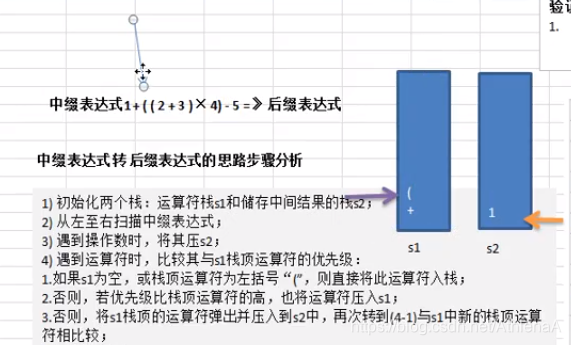
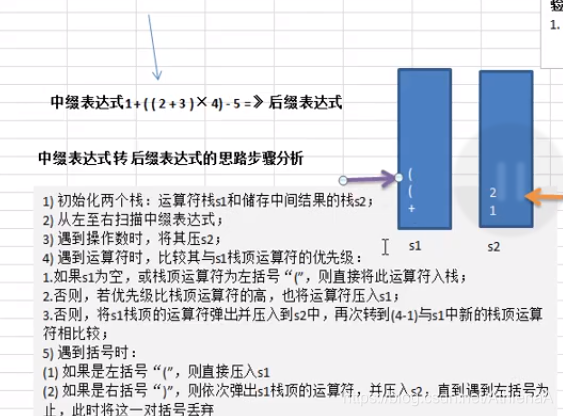
计算式:[722-5+1-5+3-3] 点击计算【如下图】
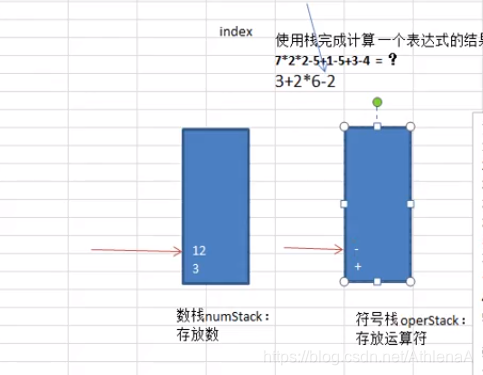
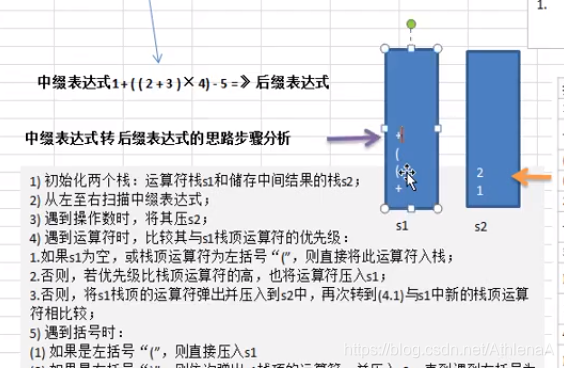
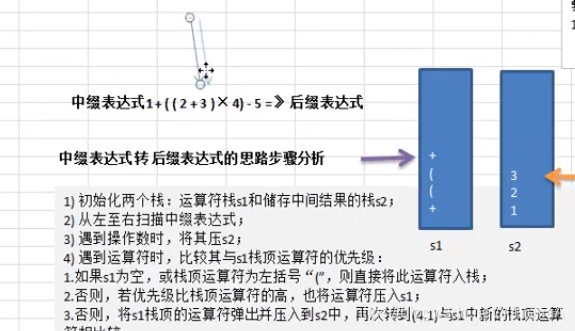
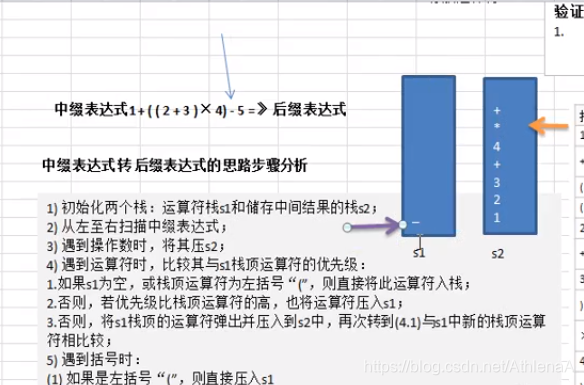
请问: 计算机底层是如何运算得到结果的? 注意不是简单的把算式列出运算,因为我们看这个算式 7 * 2 * 2 - 5, 但是计算机怎么理解这个算式的(对计算机而言,它接收到的就是一个字符串),我们讨论的是这个问题。-> 栈
栈的英文为(stack)
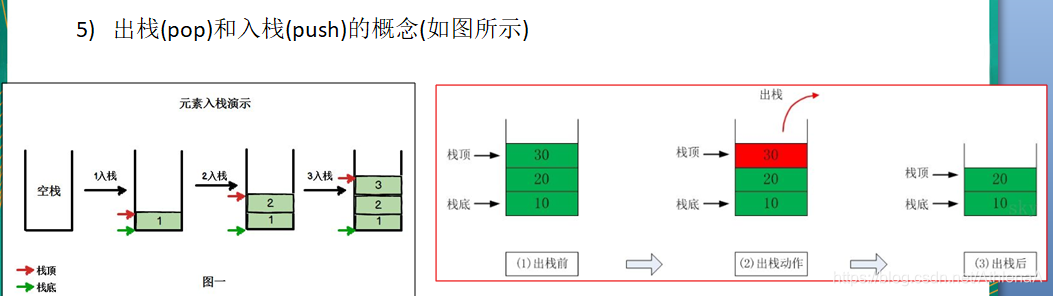
栈是一个先入后出(FILO-First In Last Out)的有序列表。
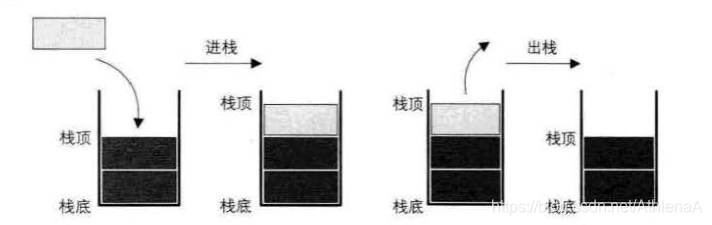
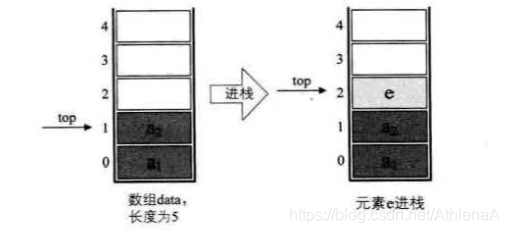
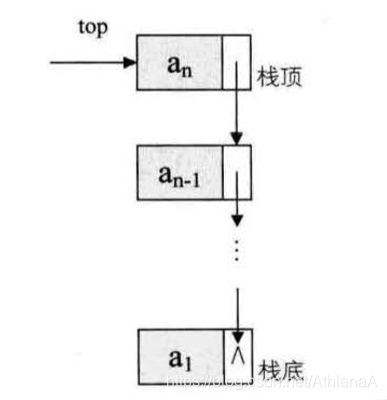
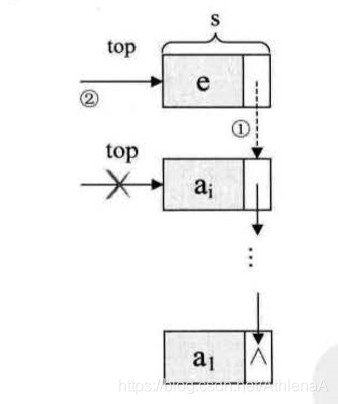
栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端,为变化的一端,称为栈顶(Top),另一端为固定的一端,称为栈底(Bottom)。
根据栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶,而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除
栈的应用场景
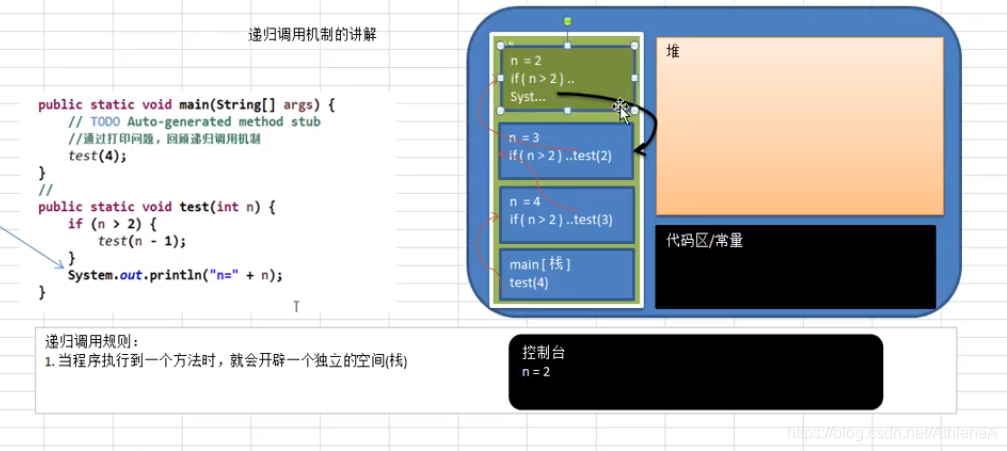
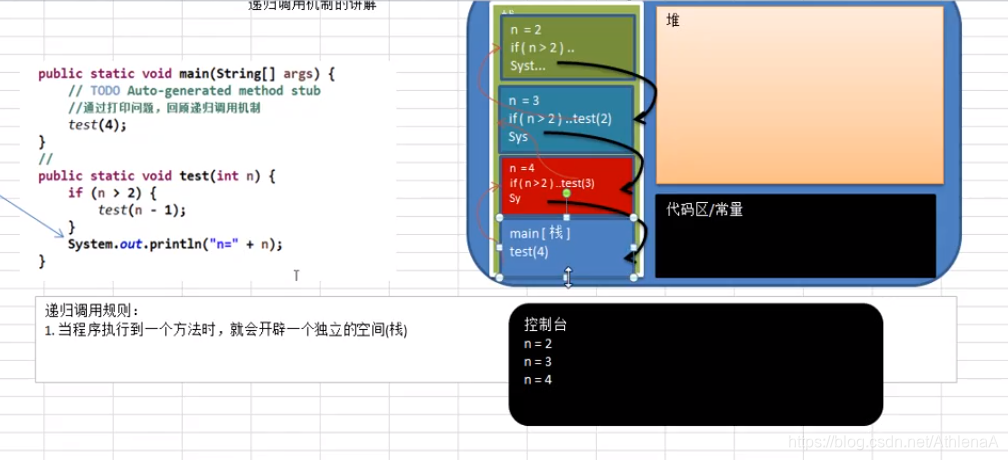
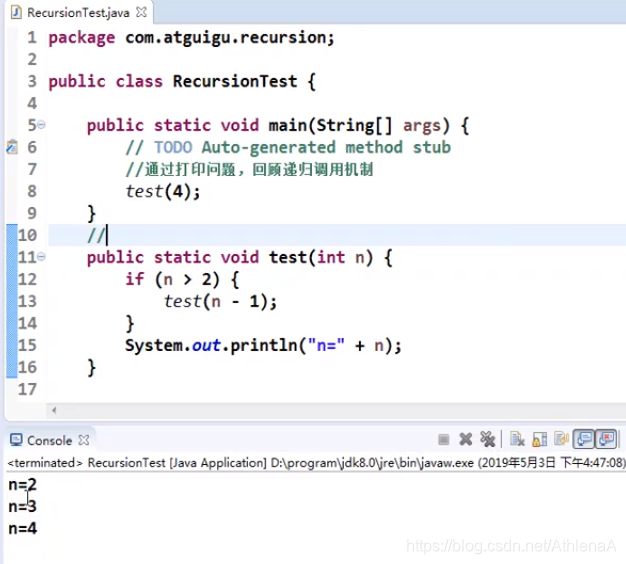
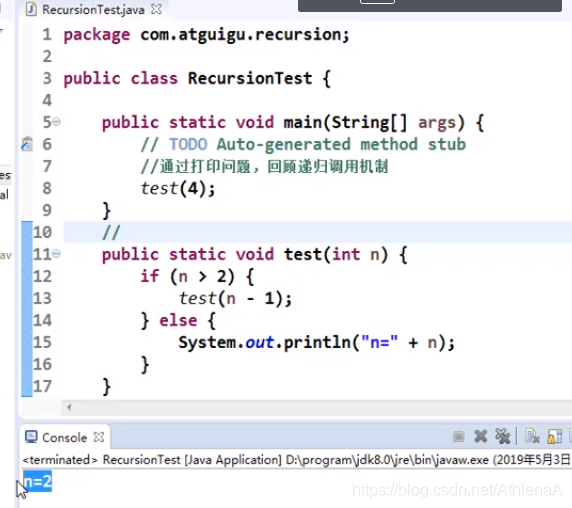
子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。
处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。
二叉树的遍历。
图形的深度优先(depth一first)搜索法。
栈的快速入门
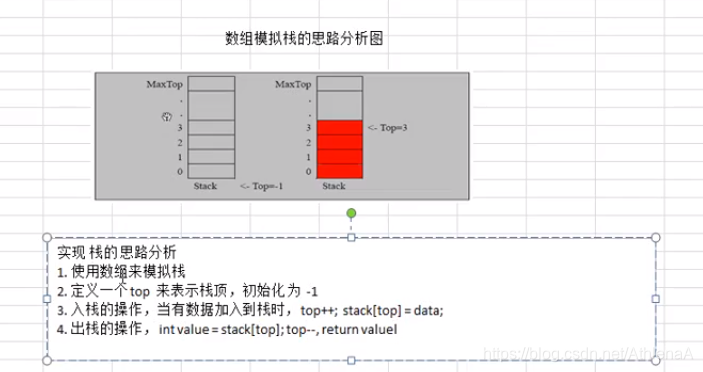
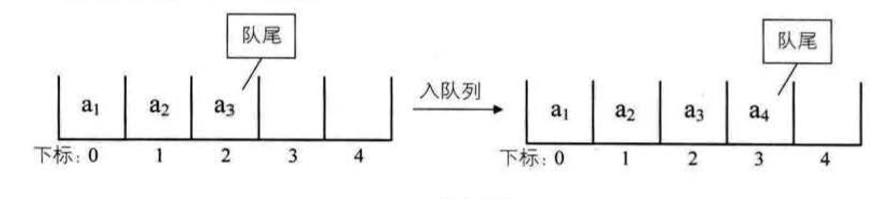
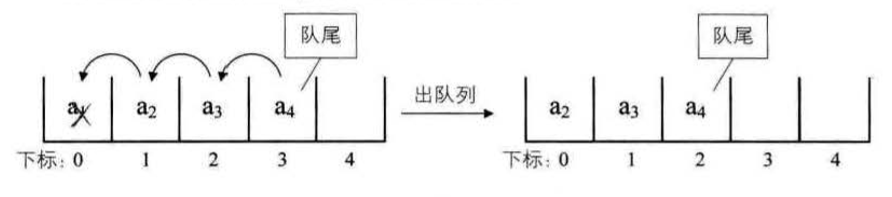
用数组模拟栈的使用,由于栈是一种有序列表,当然可以使用数组的结构来储存栈的数据内容,
下面我们就用数组模拟栈的出栈,入栈等操作。
实现思路分析,并画出示意图
对同学们加深栈的理解非常有帮助
课堂练习,将老师写的程序改成使用链表来模拟栈.
package com.zcr.stack;
import java.util.Scanner;
/**
* @author zcr
* @date 2019/7/5-21:00
*/
public class ArrayStackDemo {
public static void main(String[] args) {
//先创建一个栈对象
ArrayStack stack = new ArrayStack(4);
String key = " ";
boolean loop = true;//控制是否退出菜单
Scanner scanner = new Scanner(System.in);
while (loop) {
System.out.println("show:表示显示栈");
System.out.println("exit:退出程序");
System.out.println("push:表示添加数据到栈(入栈)");
System.out.println("pop:表示从栈取出数据(出栈)");
System.out.println("请输入你的选择");
key = scanner.next();
switch (key) {
case "show":
stack.list();
break;
case "push":
System.out.println("请输入一个数");
int value = scanner.nextInt();
stack.push(value);
break;
case "pop":
try {
int res = stack.pop();
System.out.printf("出栈的数据是%d\n",res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case "exit":
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("程序退出");
}
}
//定义栈
class ArrayStack {
private int maxSize;//栈的大小
private int[] stack;//数组,数组模拟栈,数据就放在该数组
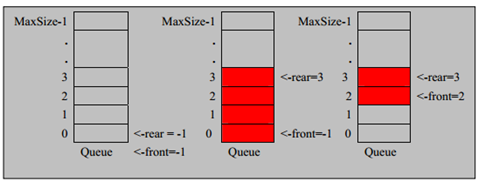
private int top = -1;
//构造器
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
//栈满
public boolean isFull() {
return top == maxSize - 1;
}
//栈空
public boolean isEmpty() {
return top == -1;
}
//入栈
public void push(int value) {
//先判断栈是否满
if (isFull()) {
System.out.println("栈满");
return;
}
top++;
stack[top] = value;
}
//出栈,将栈顶的数据返回
public int pop() {
//先判断栈是否为空
if (isEmpty()) {
//抛出异常
throw new RuntimeException("栈空,没有数据");
}
int value = stack[top];
top--;
return value;
}
//遍历栈,需要从栈顶开始显示
public void list() {
if (isEmpty()) {
System.out.println("没有数据");
return;
}
for (int i = top;i >= 0;i--) {
System.out.printf("stack[%d]=%d\n",i,stack[i]);
}
}
}
栈实现综合计算器
使用栈来实现综合计算器-自定义优先级[priority]
简化思路:
3+26-2
30+26-2
722-5+1-5+3-4
课后练习题:加入小括号.
相差48
package com.zcr.stack;
/**
* @author zcr
* @date 2019/7/5-21:38
*/
public class Calculator {
public static void main(String[] args) {
//直接把中缀表达式进行计算的
//根据前面的分析思路,完成表达式的一个运算
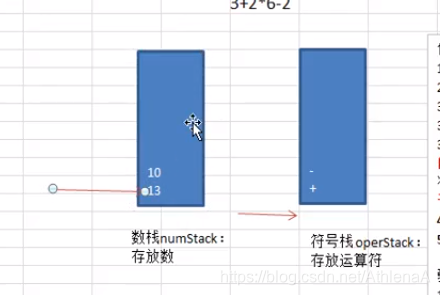
String expression = "34+2*60-2";//13 //30+2*6-2却计算不正确!如何处理多位数的问题
//创建两个栈,数字栈、符号栈
ArrayStack2 numStack = new ArrayStack2(10);
ArrayStack2 opeStack = new ArrayStack2(10);
//定义相关的变量
int index = 0;//用于扫描
int num1 = 0;
int num2 = 0;
int oper = 0;
int res = 0;
char ch = ' ';//将每次扫描得到的char保存到ch中
String keepNum = "";//用于拼接多位数
//开始用while循环扫描expression
while (true) {
//依次得到expression里面的每一个字符
ch = expression.substring(index,index+1).charAt(0);
//判断ch是什么,然后做相应的处理
if (opeStack.isOper(ch)) {//如果是运算符
//判断当前的符号栈是否为空
if (!opeStack.isEmpty()) {
//处理
//如果符号栈有操作符,就进行比较
//如果当前的操作符的优先级小于或等于栈中的操作符,就需要从数字栈中弹出两个数字
//在符号栈中弹出一个符号,进行运算,将得到结果放入到数字栈中。然后将当前的操作符入栈。
if (opeStack.priority(ch) <= opeStack.priority(opeStack.peek())) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = opeStack.pop();
res = numStack.cal(num1,num2,oper);
//把运算的结果放到数字栈中
numStack.push(res);
//把当前的操作符放到符号栈中
opeStack.push(ch);
} else {
//如果当前的操作符的优先级大于栈中的操作符,就直接入符号栈
opeStack.push(ch);
}
} else {
//符号栈如果为空,直接入符号栈
opeStack.push(ch);
}
} else {//如果是数字,择直接入数字栈
//numStack.push(ch-48);//"1+3" '1'->1
//你发现是3就入栈,后面还有数呀,这是一个多位数
//当处理多位数时,不能发现是一个数就立即入栈
//当处理数字时,需要向expression的表达式的index后面再看一位,如果是数就进行扫描,如果是符号再入栈
//因此我们需要定义一个字符串变量,用于拼接
//处理多位数
keepNum += ch;
//判断下一个字符是不是数字,如果是数字,则进行继续扫描,拼接
//如果ch已经是表达式的最后一位了,就直接入栈
if (index == expression.length() - 1) {
numStack.push(Integer.parseInt(keepNum));
} else {
if (opeStack.isOper(expression.substring(index + 1,index + 2).charAt(0))) {//只是往后面看一位,index本身不要变
//如果是运算符,则直接入数字栈
numStack.push(Integer.parseInt(keepNum));//"1"->1字符串转为数字,用Integer.parserInt
//重要!!!keepNum要清空
keepNum = "";
}
}
}
//让index+1,并判断是否扫描到expression的最后了
index++;
if (index >= expression.length()){
break;
}
}
//当表达式扫描完毕,就顺序的从数字栈和符号栈中pop出响应的数字和符号进行计算
while (true) {
//如果符号栈为空,则计算结束,数字栈中只有一个数字了就是结果
if (opeStack.isEmpty()) {
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = opeStack.pop();
res = numStack.cal(num1,num2,oper);
numStack.push(res);//入栈
}
System.out.printf("表达式%s = %d",expression,numStack.pop());
}
}
//定义栈
class ArrayStack2 {
private int maxSize;//栈的大小
private int[] stack;//数组,数组模拟栈,数据就放在该数组
private int top = -1;
//构造器
public ArrayStack2(int maxSize) {
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
//返回当前栈顶的元素
public int peek() {
return stack[top];
}
//栈满
public boolean isFull() {
return top == maxSize - 1;
}
//栈空
public boolean isEmpty() {
return top == -1;
}
//入栈
public void push(int value) {
//先判断栈是否满
if (isFull()) {
System.out.println("栈满");
return;
}
top++;
stack[top] = value;
}
//出栈,将栈顶的数据返回
public int pop() {
//先判断栈是否为空
if (isEmpty()) {
//抛出异常
throw new RuntimeException("栈空,没有数据");
}
int value = stack[top];
top--;
return value;
}
//遍历栈,需要从栈顶开始显示
public void list() {
if (isEmpty()) {
System.out.println("没有数据");
return;
}
for (int i = top;i >= 0;i--) {
System.out.printf("stack[%d]=%d\n",i,stack[i]);
}
}
//返回运算符的优先级,优先级是程序员来确定的,优先级使用数字表示
//数字越大,优先级越高
public int priority(int oper) {
if (oper == '*' || oper == '/') {//int和char都是底层用数字来比较的
return 1;
} else if (oper == '+' || oper == '-') {
return 0;
} else {
return -1;//假定目前的表达式只有+ - * 、
}
}
//判断是不是一个运算符
public boolean isOper(char val) {
return val == '+' || val == '-' || val == '*' || val == '/';
}
//计算方法
public int cal(int num1,int num2,int oper) {
int res = 0;//用于存放计算的结果
switch (oper) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;//把后弹出来的那个数作为减数。注意顺序
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num2 / num1;
break;
default:
break;
}
return res;
}
}
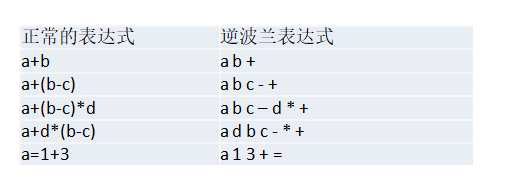
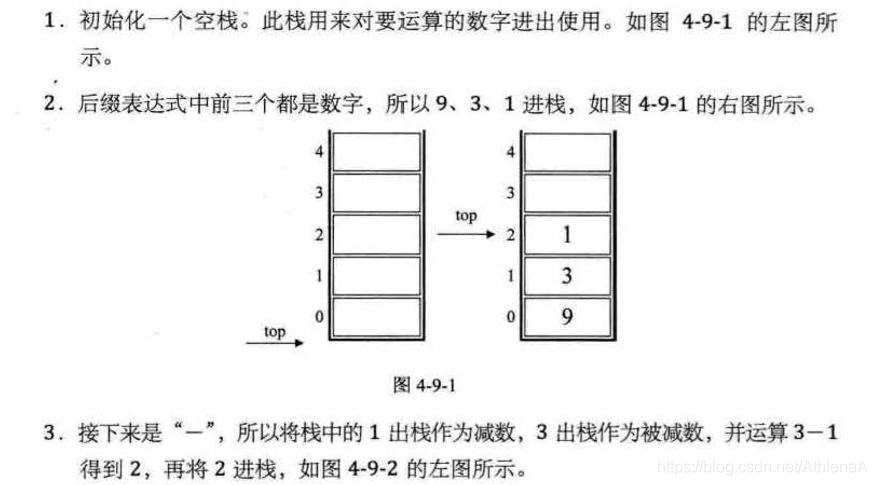
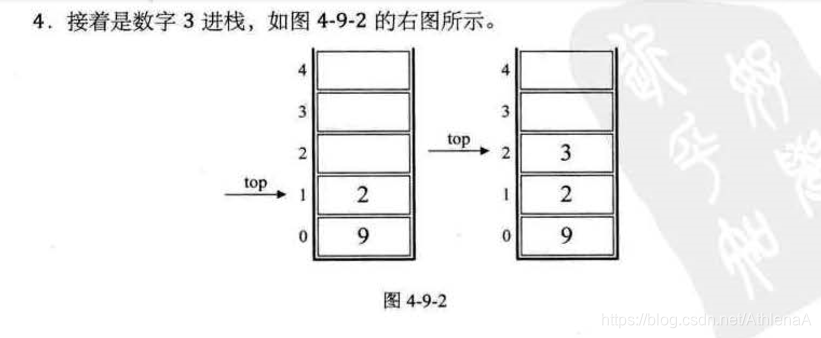
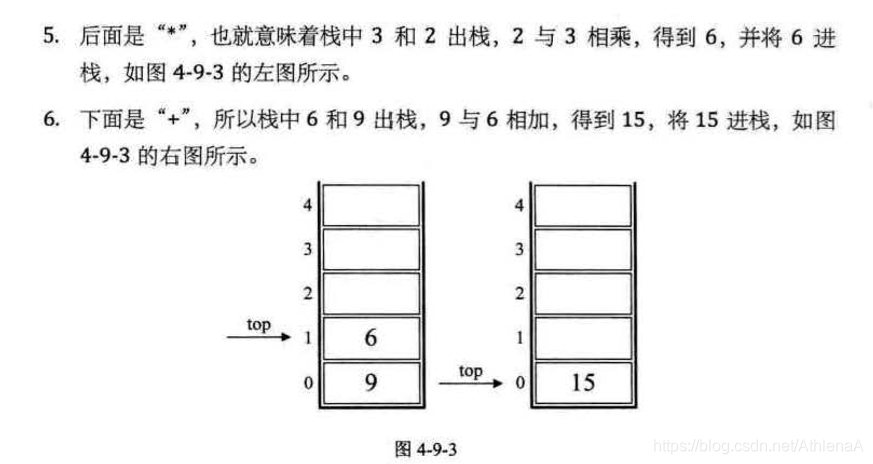
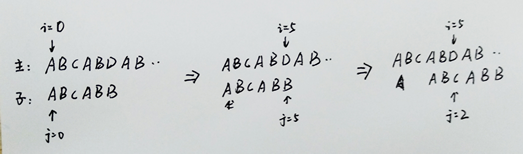
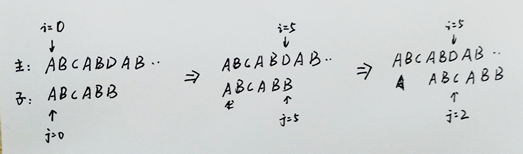
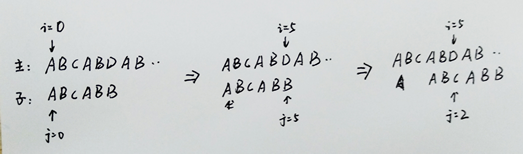
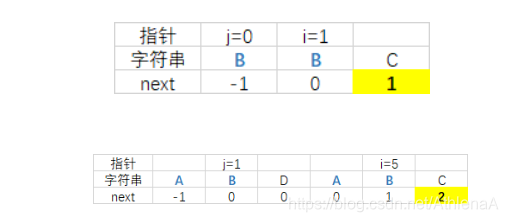
前缀、中缀、后缀表达式(逆波兰表达式)
前缀表达式(波兰表达式)
前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前
举例说明: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6
前缀表达式的计算机求值
从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果
例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:
从右至左扫描,将6、5、4、3压入堆栈
遇到+运算符,因此弹出3和4(3为栈顶元素,4为次顶元素),计算出3+4的值,得7,再将7入栈
接下来是×运算符,因此弹出7和5,计算出7×5=35,将35入栈
最后是-运算符,计算出35-6的值,即29,由此得出最终结果
中缀表达式
中缀表达式就是常见的运算表达式,如(3+4)×5-6
中缀表达式的求值是我们人最熟悉的,但是对计算机来说却不好操作(前面我们讲的案例就能看的这个问题),因此,在计算结果时,往往会将中缀表达式转成其它表达式来操作(一般转成后缀表达式.)
后缀表达式
后缀表达式又称逆波兰表达式,与前缀表达式相似,只是运算符位于操作数之后
中举例说明: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –
再比如:
后缀表达式的计算机求值
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:
从左至右扫描,将3和4压入堆栈;
遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素),计算出3+4的值,得7,再将7入栈;
将5入栈;
接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;
将6入栈;
最后是-运算符,计算出35-6的值,即29,由此得出最终结果
逆波兰计算器
我们完成一个逆波兰计算器,要求完成如下任务:
输入一个逆波兰表达式(后缀表达式),使用栈(Stack), 计算其结果
支持小括号和多位数整数,因为这里我们主要讲的是数据结构,因此计算器进行简化,只支持对整数的计算。
思路分析
代码完成
package com.zcr.stack;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
/**
* @author zcr
* @date 2019/7/5-22:36
*/
public class PolandNotation {
public static void main(String[] args) {
//先定义一个逆波兰表达式
//说明为了方便,逆波兰表达式的数字和符号使用空格隔开
String suffixExpression = "30 4 + 5 * 6 -";
//思路
//1.先将"3 4 + 5 * 6 -"放到ArrayList中
//2.将ArrayList传递给一个方法,遍历ArrayList配合栈完成计算
List<String> rpnList = getListString(suffixExpression);
System.out.println(rpnList);
int res = calculate(rpnList);
System.out.println("计算结果是="+res);
}
//将一个逆波兰表达式,依次将数字和运算符放到ArrayList中
public static List<String> getListString(String suffixExpression) {
//将suffixExpression分割
String[] split = suffixExpression.split(" ");
List<String> list = new ArrayList<String>();
for (String ele : split) {
list.add(ele);
}
return list;
}
//完成对逆波兰表达式的运算
/**
* 对list的遍历
*/
public static int calculate(List<String> ls) {
//创建一个栈
Stack<String> stack = new Stack<String>();
//遍历ls
for (String item : ls) {
//这里使用正则表达式来取出数字
if (item.matches("\\d+")) {//匹配的是多位数
//直接入栈
stack.push(item);
} else {//如果是符号
//从栈中弹出两个数,运算,再入栈
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
if (item.equals("+")) {
res = num1 + num2;
} else if (item.equals("-")) {
res = num1 - num2;
} else if (item.equals("*")) {
res = num1 * num2;
} else if (item.equals("/")) {
res = num1 / num2;
} else {
throw new RuntimeException("运算符有误");
}
//把res入栈
stack.push(res + "");
}
}
//最后留在stack中的数据就是运算结果了
return Integer.parseInt(stack.pop());
}
}
中缀表达式转换为后缀表达式
大家看到,后缀表达式适合计算式进行运算,但是人却不太容易写出来,尤其是表达式很长的情况下,因此在开发中,我们需要将 中缀表达式转成后缀表达式。
具体步骤如下:
1.初始化两个栈:运算符栈s1和储存中间结果的栈s2;
2.从左至右扫描中缀表达式;
3.遇到操作数时,将其压s2;
4.遇到运算符时,比较其与s1栈顶运算符的优先级:
1如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
2否则,若优先级比栈顶运算符的高,也将运算符压入s1;
3否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中新的栈顶运算符相比较;
5.遇到括号时:(1) 如果是左括号“(”,则直接压入s1(2) 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
6.重复步骤2至5,直到表达式的最右边
7.将s1中剩余的运算符依次弹出并压入s2
8.依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式
举例说明:
将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程如下
因此结果为
“1 2 3 + 4 × + 5 –”
代码实现中缀表达式转为后缀表达式
package com.zcr.stack;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
/**
* @author zcr
* @date 2019/7/5-22:36
*/
public class PolandNotation {
public static void main(String[] args) {
/*//先定义一个逆波兰表达式
//说明为了方便,逆波兰表达式的数字和符号使用空格隔开
String suffixExpression = "30 4 + 5 * 6 -";
//思路
//1.先将"3 4 + 5 * 6 -"放到ArrayList中
//2.将ArrayList传递给一个方法,遍历ArrayList配合栈完成计算
List<String> rpnList = getListString(suffixExpression);
System.out.println(rpnList);
int res = calculate(rpnList);
System.out.println("计算结果是="+res);*/
//完成将一个中缀表达式转成后缀表达式的功能
//说明:先将中缀表达式转换成对应的List
String expression = "1+((2+3)*4)-5";
List<String> infixExpressionList = toInfixExpressionList(expression);
System.out.println("中缀表达式对应的List"+infixExpressionList);//[1, +, (, (, 2, +, 3, ), *, 4, ), -, 5]
//将得到的中缀表达式列表转成后缀表达式对应的额List
List<String> parseSuffixExpressionList = parseSuffixExpressionList(infixExpressionList);
System.out.println("后缀表达式对应的List"+parseSuffixExpressionList);//[1, 2, 3, +, 4, *, +, 5, -]
}
//将一个逆波兰表达式,依次将数字和运算符放到ArrayList中
public static List<String> getListString(String suffixExpression) {
//将suffixExpression分割
String[] split = suffixExpression.split(" ");
List<String> list = new ArrayList<String>();
for (String ele : split) {
list.add(ele);
}
return list;
}
//完成对逆波兰表达式的运算
/**
* 对list的遍历
*/
public static int calculate(List<String> ls) {
//创建一个栈
Stack<String> stack = new Stack<String>();
//遍历ls
for (String item : ls) {
//这里使用正则表达式来取出数字
if (item.matches("\\d+")) {//匹配的是多位数
//直接入栈
stack.push(item);
} else {//如果是符号
//从栈中弹出两个数,运算,再入栈
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
if (item.equals("+")) {
res = num1 + num2;
} else if (item.equals("-")) {
res = num1 - num2;
} else if (item.equals("*")) {
res = num1 * num2;
} else if (item.equals("/")) {
res = num1 / num2;
} else {
throw new RuntimeException("运算符有误");
}
//把res入栈
stack.push(res + "");
}
}
//最后留在stack中的数据就是运算结果了
return Integer.parseInt(stack.pop());
}
//将中缀表达式转成对应的List
public static List<String> toInfixExpressionList(String s) {
//定义一个List,存放中缀表达式对应的内容
List<String> ls = new ArrayList<String>();
int i = 0;//这是一个指针,用于遍历中缀表达式字符串
String str;//对多位数进行拼接
char c;//每遍历一个字符,就放到x
do {
//如果c是一个非数字,就需要加入到ls中
if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
ls.add(""+c);
i++;//i需要后移
} else {//如果是一个数,要考虑多位数
str = "";//先将str置为空值 '0'[48]->'9'[57]
while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
str += c;//拼接
i++;
}
ls.add(str);
}
}while (i < s.length());
return ls;
}
//中缀表达式列表转换成后缀表达式列表
public static List<String> parseSuffixExpressionList(List<String> ls) {
//定义两个栈
Stack<String> s1 = new Stack<String>();//符号栈
//存储中间结果的栈,这个栈在整个转换过程中没有pop的操作,而且后面还需要逆序输出,所以使用ArrayList结构实现
List<String> s2 = new ArrayList<String>();
//遍历ls
for (String item : ls) {
//如果是一个数,就入栈s2
if (item.matches("\\d+")) {
s2.add(item);
} else if (item.equals("(")) {
s1.push("(");
} else if (item.equals(")")) {
//如果是右括号,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
while (!s1.peek().equals("(")) {
s2.add(s1.pop());
}
s1.pop();//将(弹出,消除这一对小括号
} else {
//当item是一个运算符且优先级小于等于s1栈顶的运算符的优先级
//将s1栈顶的运算符弹出并压入到s2,再次转到前面与s1中的新栈顶运算符比较
//问题:我们缺少一个比较优先级高级的方法
while (s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)) {
s2.add(s1.pop());
}
//还需要将item压入栈中
//若item是一个运算符且优先级大于s1栈顶的运算符的优先级
s1.push(item);
}
}
//将s1中剩余的运算符依次弹出加入到s2中
while (s1.size() != 0) {
s2.add(s1.pop());
}
return s2;//因为是存放到List中的,因此按顺序输出就是对应的后缀表达式对应的list
}
}
//比较运算符比较级高低,返回一个运算符对应的优先级
class Operation {
private static int ADD = 1;
private static int SUB = 1;
private static int MUL = 2;
private static int DIV = 2;
//写一个方法,返回对应的优先级数字
public static int getValue(String operation) {
int result = 0;
switch (operation) {
case "+":
result = ADD;
break;
case "-":
result = SUB;
break;
case "*":
result = MUL;
break;
case "/":
result = DIV;
break;
default:
System.out.println("不存在该运算符");
break;
}
return result;
}
}
逆波兰计算器完整版
完整版的逆波兰计算器,功能包括
支持 + - * / ( )
多位数,支持小数,
兼容处理, 过滤任何空白字符,包括空格、制表符、换页符
逆波兰计算器完整版考虑的因素较多,下面给出完整版代码供同学们学习,其基本思路和前面一样,也是使用到:中缀表达式转后缀表达式。
package com.zcr.stack;
import sun.awt.Symbol;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Stack;
import java.util.regex.Pattern;
/**
* @author zcr
* @date 2019/7/6-17:29
*/
public class ReversePolishMultiCalc {
/**
* 匹配 + - * / ( ) 运算符
*/
static final String SYMBOL = "\\+|-|\\*|/|\\(|\\)";
static final String LEFT = "(";
static final String RIGHT = ")";
static final String ADD = "+";
static final String MINUS= "-";
static final String TIMES = "*";
static final String DIVISION = "/";
/**
* 加減 + -
*/
static final int LEVEL_01 = 1;
/**
* 乘除 * /
*/
static final int LEVEL_02 = 2;
/**
* 括号
*/
static final int LEVEL_HIGH = Integer.MAX_VALUE;
static Stack<String> stack = new Stack<>();
static List<String> data = Collections.synchronizedList(new ArrayList<String>());
/**
* 去除所有空白符
* @param s
* @return
*/
public static String replaceAllBlank(String s ){
// \\s+ 匹配任何空白字符,包括空格、制表符、换页符等等, 等价于[ \f\n\r\t\v]
return s.replaceAll("\\s+","");
}
/**
* 判断是不是数字 int double long float
* @param s
* @return
*/
public static boolean isNumber(String s){
Pattern pattern = Pattern.compile("^[-\\+]?[.\\d]*$");
return pattern.matcher(s).matches();
}
/**
* 判断是不是运算符
* @param s
* @return
*/
public static boolean isSymbol(String s){
return s.matches(SYMBOL);
}
/**
* 匹配运算等级
* @param s
* @return
*/
public static int calcLevel(String s){
if("+".equals(s) || "-".equals(s)){
return LEVEL_01;
} else if("*".equals(s) || "/".equals(s)){
return LEVEL_02;
}
return LEVEL_HIGH;
}
/**
* 匹配
* @param s
* @throws Exception
*/
public static List<String> doMatch (String s) throws Exception{
if(s == null || "".equals(s.trim())) throw new RuntimeException("data is empty");
if(!isNumber(s.charAt(0)+"")) throw new RuntimeException("data illeagle,start not with a number");
s = replaceAllBlank(s);
String each;
int start = 0;
for (int i = 0; i < s.length(); i++) {
if(isSymbol(s.charAt(i)+"")){
each = s.charAt(i)+"";
//栈为空,(操作符,或者 操作符优先级大于栈顶优先级 && 操作符优先级不是( )的优先级 及是 ) 不能直接入栈
if(stack.isEmpty() || LEFT.equals(each)
|| ((calcLevel(each) > calcLevel(stack.peek())) && calcLevel(each) < LEVEL_HIGH)){
stack.push(each);
}else if( !stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek())){
//栈非空,操作符优先级小于等于栈顶优先级时出栈入列,直到栈为空,或者遇到了(,最后操作符入栈
while (!stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek()) ){
if(calcLevel(stack.peek()) == LEVEL_HIGH){
break;
}
data.add(stack.pop());
}
stack.push(each);
}else if(RIGHT.equals(each)){
// ) 操作符,依次出栈入列直到空栈或者遇到了第一个)操作符,此时)出栈
while (!stack.isEmpty() && LEVEL_HIGH >= calcLevel(stack.peek())){
if(LEVEL_HIGH == calcLevel(stack.peek())){
stack.pop();
break;
}
data.add(stack.pop());
}
}
start = i ; //前一个运算符的位置
}else if( i == s.length()-1 || isSymbol(s.charAt(i+1)+"") ){
each = start == 0 ? s.substring(start,i+1) : s.substring(start+1,i+1);
if(isNumber(each)) {
data.add(each);
continue;
}
throw new RuntimeException("data not match number");
}
}
//如果栈里还有元素,此时元素需要依次出栈入列,可以想象栈里剩下栈顶为/,栈底为+,应该依次出栈入列,可以直接翻转整个stack 添加到队列
Collections.reverse(stack);
data.addAll(new ArrayList<>(stack));
System.out.println(data);
return data;
}
/**
* 算出结果
* @param list
* @return
*/
public static Double doCalc(List<String> list){
Double d = 0d;
if(list == null || list.isEmpty()){
return null;
}
if (list.size() == 1){
System.out.println(list);
d = Double.valueOf(list.get(0));
return d;
}
ArrayList<String> list1 = new ArrayList<>();
for (int i = 0; i < list.size(); i++) {
list1.add(list.get(i));
if(isSymbol(list.get(i))){
Double d1 = doTheMath(list.get(i - 2), list.get(i - 1), list.get(i));
list1.remove(i);
list1.remove(i-1);
list1.set(i-2,d1+"");
list1.addAll(list.subList(i+1,list.size()));
break;
}
}
doCalc(list1);
return d;
}
/**
* 运算
* @param s1
* @param s2
* @param symbol
* @return
*/
public static Double doTheMath(String s1,String s2,String symbol){
Double result ;
switch (symbol){
case ADD : result = Double.valueOf(s1) + Double.valueOf(s2); break;
case MINUS : result = Double.valueOf(s1) - Double.valueOf(s2); break;
case TIMES : result = Double.valueOf(s1) * Double.valueOf(s2); break;
case DIVISION : result = Double.valueOf(s1) / Double.valueOf(s2); break;
default : result = null;
}
return result;
}
public static void main(String[] args) {
//String math = "9+(3-1)*3+10/2";
String math = "12.8 + (2 - 3.55)*4+10/5.0";
try {
doCalc(doMatch(math));
} catch (Exception e) {
e.printStackTrace();
}
}
}
4.2.1栈的定义 89
栈(stack)是限定仅在表尾进行插入和删除操作的线性表
我们把允许插入和删除的一端称为栈顶 (top) ,另一端称为栈底 (bottom) ,不含任何数据元素的棋称为空栈。 栈是一种后进先出(Last In First Out)的线性表,简称LIFO结构。
首先它是一个统性表,也就是说,栈元素具有线性关系,即前驱后继关系。只不过它是一种特殊的线性表而已。定义中说是在线性表的表尾进行插入和删除操作,这里表尾是指栈顶,而不是栈底。
它的特殊之处就在于限制了这个线性表的插入和删除位置,它始终只在栈顶进 行。这也就使得栈底是固定的,最先进栈的只能在栈底。
栈的插入操作,叫作进栈,也称压栈、入栈。
栈的删除操作,叫做出栈,也有的叫做弹栈。
4.2.2进栈出栈变化形式 90
这个最先进栈的元素,是不是就只能是最后出栈呢?
答案是不一定,要看什么情况。栈对线性表的插入和删除的位置进行了限制 ,并没有对元素进出的时间进行限制,也就是说,在不是所有元素都进栈的情况下,事先进去的元素 也可以出栈,只要保证是栈顶元素出栈就可以。
举例来说,如果我们现在是有 3 个整型数字元素 1、 2、 3 依次进栈,会有哪些出栈次序呢?
• 第一种: 1 、 2、 3 进,再 3、 2、 1 出。这是最简单的最好理解的一种,出栈次序为 321。
• 第二种: 1 进, 1 出, 2 进. 2 出, 3 进, 3 出。也就是进一个就出一个,出栈次序为 123。
• 第三种: 1 进, 2 进, 2 出, 1 出, 3 进, 3 出。出栈次序为 213。
• 第四种: 1 进, 1 出, 2 进, 3 进, 3 出, 2 出。出栈次序为 132.
• 第五种:: 1 进, 2 进, 2 出, 3 进, 3 出, 1 出。 出栈次序为 231。
有没有可能是 312 这样的次序出钱呢?答案是肯定不会。因为 3 先出栈,就意味 着, 3 曾经进栈,既然 3 都进栈了,那也就意味着, 1 和 2 已经进栈了,此时, 2 一 定是在 1 的上面,就是更接近栈顶,那么出栈只可能是 321,不然不满足 123 依次进 栈的要求,所以此时不会发生 1 比 2 先出栈的情况。
从这个简单的例子就能看出,只是 3 个元素,就有 5 种可能的出枝次序,如果元 素数量多,其实出梭的变化将会更多的。这个知识点一定要弄明白。
4.3栈的抽象数据类型 91
对于栈来讲,理论上线性表的操作特性它都具备,可由于它的特殊性,所以针对 它在操作上会有些变化。特别是插入和删除操作,我们改名为 push 和 pop,英文直译 的话是压和弹,更容易理解。你就把官当成是弹夹的子弹压人和弹出就好记忆了,我 们一般叫进栈和出栈。
由于栈本身就是一个线性表,那么上一章我们讨论了线性表的顺序存储和链式存 储,对于栈来说,也是同样适用的。
4.4栈的顺序存储结构及实现 92
4.4.1栈的顺序存储结构 92
既然栈是线性表的特例,那么栈的顺序存储其实也是线性表顺序存储的简化,我 们简称为顺序栈。 线性表是用数组来实现的,想想看,对于栈这种只能一头插入删除 的线性表来说,用数组哪一端来作为栈顶和栈底比较好?
对,没错,下标为 0 的一端作为栈底比较好,因为首元素都存在栈底,变化最 小,所以让它作栈底。
我们定义一个 top 变量来指示栈顶元素在数组中的位置,枝顶的 top 可以变大变小。若存储栈的长度为 StackSize,则栈顶位置 top 必须小于StackSize。 当栈存在一个元素时,top 等于 0,因此通常把空栈的判定条件定为 top 等于-1。
栈的结构定义:
public class SqStack<E> {
private E[] data;
private int top; //栈顶指针,top=-1时为空栈
private int maxSize;
private static final int DEFAULT_SIZE= 10;
public SqStack() {
this(DEFAULT_SIZE);
}
public SqStack(int maxSize) {
//无法创建泛型数组 data=new E[maxSize];
data=(E[]) new Object[maxSize];
top=-1;
this.maxSize=maxSize;
}
若现在有一个栈, StackSize 是 5 ,则栈普通情况、空栈和栈满的情况示意图如图:
4.4.2栈的顺序存储结构进栈操作 93
public void push(E e) {
if(top==maxSize-1)
throw new RuntimeException(“栈已满,无法进栈!”);
top++;
data[top]=e;
}
4.4.3栈的顺序存储结构出栈操作 94
public E pop() {
if(top==-1)
throw new RuntimeException("空栈,无法出栈!");
E e=data[top];
top--;
return e;
}
两者没有涉及到任何循环语句,因此时间复杂度均是O(1)。
顺序栈的代码
/**
* 栈的顺序储存结构
*
* 问题:构造器中,泛型数组创建是否有更好的方法?
* @author Yongh
*
*/
public class SqStack<E> {
private E[] data;
private int top; //栈顶指针,top=-1时为空栈
private int maxSize;
private static final int DEFAULT_SIZE= 10;
public SqStack() {
this(DEFAULT_SIZE);
}
public SqStack(int maxSize) {
//无法创建泛型数组 data=new E[maxSize];
data=(E[]) new Object[maxSize];
top=-1;
this.maxSize=maxSize;
}
public void push(E e) {
if(top==maxSize-1)
throw new RuntimeException("栈已满,无法进栈!");
top++;
data[top]=e;
}
public E pop() {
if(top==-1)
throw new RuntimeException("空栈,无法出栈!");
E e=data[top];
top--;
return e;
}
public void printStack() {
if(top==-1) {
System.out.println("空栈");
}else {
for(int i=0;i<=top;i++) {
System.out.println(data[i]);
}
}
}
}
测试代码
public class StackTest {
public static void main(String[] args) {
SqStack<Student> sqStack=new SqStack<Student>();
Student[] students= {new Student("小A",11),new Student("小B",12),new Student("小C",13),
new Student("小D",14),new Student("小E",151)};
for(int i=0;i<5;i++) {
sqStack.push(students[i]);
}
sqStack.printStack();
for(int i=0;i<5;i++) {
sqStack.pop();
}
sqStack.printStack();
}
}
class Student{
public Student(String name, int age) {
this.name=name;
this.age=age;
}
String name;
int age;
public String toString() {
return name;
}
}
小A
小B
小C
小D
小E
空栈
4.5两栈共享空间 94
两个大学室友毕业同时到北京工作,他们都希望租房时能找到独自住的一室户或一室一厅,可找来找去发现,实在是承受不起。
其实栈的顺序存储还是很方便的,因为它只准栈顶迸出元素,所以不存在线性表 插入和删除时需要移动元素的问题。不过它有一个很大的缺陷,就是必须事先确定数组存储空间大小,万一不够用了,就需要编程手段来扩展数组的容量,非常麻烦。 对 于一个栈,我们也只能尽量考虑周全,设计出合适大小的数组来处理,但对于两个相 同类型的栈,我们却可以做到最大限度地利用其事先开辟的存储空间来进行操作。
如果我们有两个相同类型的栈,我们为它们各自开辟了数组空间, 极有可能是第一个栈已经满了,再进栈就溢出了,而另一个栈还有很多存储空间空 闲。 这又何必呢?我们完全可以用一个数组来存储两个栈,只不过需要点小技巧。
数组有两个端点,两个栈有两个栈底,让一个栈的栈底为 数组的始端,即下标为 0 处,另一个栈为栈的末端,即下标为数组长度 n-l 处。这样,两个栈如果增加元素,就是两端点向中间延伸。
其实关键思路是:它们是在数组的两端,向中间靠拢。 topl 和 top2 是栈1 和栈 2 的栈顶指针,可以想象,只要它们俩不见面,两个栈就可以一直使用。
从这里也就可以分析出来,栈 1 为空时,就是 topl 等于一 1 时;而当 top2 等于 n 时,即是栈 2 为空时,那什么时候栈满呢?
想想极端的情况,若栈2 是空栈,栈 1 的 topl 等于 n-l 时,就是栈 1 满了。 反 之,当栈 1 为空栈时,top2 等于 0 时,为栈 2 满。 但更多的情况,其实就是我刚才 说的,两个栈见面之时,也就是两个指针之间相差 1 时,即 回top1 + 1 == top2 为栈满。
两栈共享空间的结构的代码如下:
public class SqDoubleStack<E> {
private E[] data;
private int top1; //栈1栈顶指针,top=-1时为空栈
private int top2; //栈2栈顶指针,top=maxSize-1时为空栈
private int maxSize;
private static final int DEFAULT_SIZE= 10;
public SqDoubleStack() {
this(DEFAULT_SIZE);
}
public SqDoubleStack(int maxSize) {
//无法创建泛型数组 data=new E[maxSize];
data=(E[]) new Object[maxSize];
top1=-1;
top2=maxSize-1;
this.maxSize=maxSize;
}
对于两栈共享空间的 push 方法,我们除了要插入元素值参数外,还需要有一个判 断是栈 1 还是栈 2 的栈号参数 stackNumber。插入元素的代码如下:
/*
* 进栈操作,stackNumber代表要进的栈号
*/
public void push(int stackNumber,E e) {
if(top1+1top2)
throw new RuntimeException(“栈已满,无法进栈!”);
if(stackNumber1) {
data[++top1]=e;
}else if(stackNumber==2) {
data[–top2]=e;
}else {
throw new RuntimeException(“栈号错误!”);
}
}
因为在开始已经判断了是否有栈满的情况,所以后面的 topl+1 或 top2-1 是不担 心溢出问题的。
对于两栈共享空间的 pop 方法,参数就只是判断栈 1 栈 2 的参数 S1ackNumber. 代码如下:
/*
* 出栈操作
*/
public E pop(int stackNumber) {
E e;
if(stackNumber1){
if(top1-1)
throw new RuntimeException(“空栈1,无法出栈!”);
e=data[top1–];
}else if(stackNumber2) {
if(top2maxSize-1)
throw new RuntimeException(“空栈2,无法出栈!”);
e=data[top2++];
}else {
throw new RuntimeException(“栈号错误!”);
}
return e;
}
事实上,使用这样的数据结构,通常都是当两个栈的空间需求有相反关系时,也 就是一个栈增长时另一个栈在缩短的情况。就像买卖股票一样,你买入时,一定是有 一个你不知道的人在做卖出操作. 有人赚钱,就一定是有人赔钱。这样使用两栈共享 空间存储方法才有比较大的意义. 否则两个栈都在不停地增长,那很快就会因栈满而 溢出了。
当然,这只是针对两个具有相同数据类型的栈的一个设计上的技巧,如果是不相同数据类型的栈,这种办法不但不能更好地处理问题,反而会使问题变得更复杂,大 家要注意这个前提。
两栈共享空间代码
/**
* 栈的顺序储存结构(两栈共享空间)
*
* 注意点:栈满条件为top1+1==top2
*
* @author Yongh
*
*/
public class SqDoubleStack<E> {
private E[] data;
private int top1; //栈1栈顶指针,top=-1时为空栈
private int top2; //栈2栈顶指针,top=maxSize-1时为空栈
private int maxSize;
private static final int DEFAULT_SIZE= 10;
public SqDoubleStack() {
this(DEFAULT_SIZE);
}
public SqDoubleStack(int maxSize) {
//无法创建泛型数组 data=new E[maxSize];
data=(E[]) new Object[maxSize];
top1=-1;
top2=maxSize-1;
this.maxSize=maxSize;
}
/*
* 进栈操作,stackNumber代表要进的栈号
*/
public void push(int stackNumber,E e) {
if(top1+1==top2)
throw new RuntimeException("栈已满,无法进栈!");
if(stackNumber==1) {
data[++top1]=e;
}else if(stackNumber==2) {
data[--top2]=e;
}else {
throw new RuntimeException("栈号错误!");
}
}
/*
* 出栈操作
*/
public E pop(int stackNumber) {
E e;
if(stackNumber==1){
if(top1==-1)
throw new RuntimeException("空栈1,无法出栈!");
e=data[top1--];
}else if(stackNumber==2) {
if(top2==maxSize-1)
throw new RuntimeException("空栈2,无法出栈!");
e=data[top2++];
}else {
throw new RuntimeException("栈号错误!");
}
return e;
}
}
4.6栈的链式存储结构及实现 97
4.6.1栈的链式存储结构 97
栈的链式存储结构,简称为链栈。
栈只是栈顶来做插入和删除操作,栈顶放在链表的头部还是尾部呢?由于单链表有头指针,而栈顶指针也是必须的,那干吗不让它俩合二为一呢,所以比较好的办法是把栈顶放在单链表的头部。另外,都已经有了栈顶在头部了,单链表中比较常用的头结点也就失去了意义,通常对于链栈来说,是不需要头结点的。
对于链栈来说,基本不存在栈满的情况,除非内存已经没有可以使用的空间,如 果真的发生,那此时的计算机操作系统已经面临死机崩溃的情况,而不是这个链栈是否溢出的问题。
但对于空栈来说,链表原定义是头指针指向空, 那么链栈的空其实就是top=null 的时候。
链栈的结构代码如下 :
public class LinkStack<E> {
private StackNode<E> top;
private int count;
private class StackNode<E>{
E data;
StackNode<E> next;
public StackNode(E data,StackNode<E> next) {
this.data=data;
this.next=next;
}
}
public LinkStack() {
top=new StackNode<E>(null, null);
count=0;
}
链栈的操作绝大部分都和单链表类似,只是在插入和删除上,特殊一些。
4.6.2栈的链式存储结构进栈操作 98
对于链栈的进栈push 操作,假设元素值为 e 的新结点是s, top 为栈顶指针,示 意图如图
public void push(E e) {
StackNode<E> node=new StackNode<E>(e, top);
node.next=top;//把当前的栈顶元素赋值给新结点的直接后继
top=node;//将新的节点node赋值给栈顶指针
count++;
}
4.6.3栈的链式存储结构出栈操作 99
至于链栈的出栈 pop 操作,也是很简单的三句操作. 假设变量 p 用来存储要删除 的栈顶结点,将栈顶指针下移一位,最后释放 p 即可,如图
public E pop() {
if(count==0)
throw new RuntimeException("空栈,无法出栈!");
StackNode<E> node;
node=top;//将栈顶节点赋值给node
top=top.next;//使得栈顶指针下移一位,指向后一结点
count--;
E e=node.data;
node=null;//释放节点node
return e;
}
链栈代码
/**
*
* 栈的链式存储结构
*
* @author Yongh
*/
public class LinkStack<E> {
private StackNode<E> top;
private int count;
private class StackNode<E>{
E data;
StackNode<E> next;
public StackNode(E data,StackNode<E> next) {
this.data=data;
this.next=next;
}
}
public LinkStack() {
top=new StackNode<E>(null, null);
count=0;
}
public void push(E e) {
StackNode<E> node=new StackNode<E>(e, top);
node.next=top;//把当前的栈顶元素赋值给新结点的直接后继
top=node;//将新的节点node赋值给栈顶指针
count++;
}
public E pop() {
if(count==0)
throw new RuntimeException("空栈,无法出栈!");
StackNode<E> node;
node=top;
top=top.next;
count--;
E e=node.data;
node=null;
return e;
}
public void printStack() {
if(count==0) {
System.out.println("空栈");
}else {
StackNode<E> node=top;
for(int i=0;i<count;i++) {
System.out.println(node.data);
node=node.next;
}
}
}
/*
* 测试代码
*/
public static void main(String[] args) {
LinkStack<Student> linkStack=new LinkStack<Student>();
Student[] students= {new Student("小A",11),new Student("小B",12),new Student("小C",13),
new Student("小D",14),new Student("小E",151)};
for(int i=0;i<5;i++) {
linkStack.push(students[i]);
}
linkStack.printStack();
System.out.println("----");
for(int i=0;i<5;i++) {
System.out.println(linkStack.pop());
}
linkStack.printStack();
}
}
结果:
小E
小D
小C
小B
小A
小E
小D
小C
小B
小A
空栈
链栈的进栈push 和出校 pop 操作都根简单,没有任何循环操作,时间复杂度均为O(1)。
比较:
顺序栈与链栈在时间复杂度上是一样的,均为O(1)
对于空间性能,顺序栈需要事先确定一个固定的长度,可能会存在内存空间浪费的问题,但它的优势是存取时定位很方便,而链栈则要求每个元素都有指针域,这同时也增加了一些内存开销,但对于栈的长度无限制
如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈
4.7栈的作用 100
有的同学可能会觉得,用数组或链表直接实现功能不就行了吗?干吗要引入栈这样的数据结构呢?这个问题问得好。
其实这和我们明明有两只脚可以走路,干吗还要乘汽车、火车、飞机一样。理论 上,陆地上的任何地方,你都是可以靠双脚走到的,可那需要多少时间和精力呢?我 们更关注的是到达而不是如何去的过程。
栈的引人简化了程序设计的问题,划分了不同关注层次,使得思考范围缩小,更 加聚焦于我们要解决的问题核心。反之,像数组等,因为要分散精力去考虑数组的下 标增减等细节问题,反而掩盖了问题的本质。
所以现在的许多高级语言,比如 )ava、 C#等都有对栈结构的封装, 你可以不用关 注它的实现细节,就可以直接使用 Stack 的 push 和 pop 方法,非常方便。
4.8栈的应用——递归 100
当你往镜子前面一站,镜子里面就有一个你的像。但你试过两面镜子一起照吗?如果a、b两面镜子相互面对面放着,你往中间一站,嘿,两面镜子里都有你的千百个“化身”。
栈有一个很重要的应用:在程序设计语言中实现了递归。
一个经典的递归例子:斐被那契数列 (Fibonacci) 。
4.8.1斐波那契数列实现 101
说如果兔子在出生两个月后,就有繁殖能力, 一对兔子每个月能生出一对小兔子 来。假设所有兔都不死,那么一年以后可以繁殖多少对兔子呢?
我们拿新出生的一对小兔子分析一下;第一个月小兔子没有繁殖能力,所以还是 一对i 两个月后,生下一对小兔子数共有两对; 三个月以后,老兔子又生下一对,因 为小兔子还没有繁殖能力 , 所以一共是三对……依次类推可以列出下表(
表中数字 1, 1 , 2, 3 , 5, 8 , 13…构成了一个序列。这个数列有个十分明显的 特点,那是:前面相邻两项之和,构成了后一项
先考虑一下,如果我们要实现这样的数列用常规的迭代的办法如何实现?假设我 们需要打印出前 40 位的斐波那契数到数。代码如下:
但其实我们的代码, 如果用递归来实现,还 可以更简单。
函数怎么可以自己调用自己?听起来有些难以理解,不过你可以不要把一个递归 函数中调用自己的函数看作是在调用自己,而就当它是在调另一个函数。只不过,这个函数和自己长得一样而已。
4.8.2递归定义 103
在高级语言中,调用自己和其他函数并没有本质的不同。我们把一个直接调用自 己或通过一系列的调用语句间接地调用自己的函数,称做递归函数。
当然,写递归程序最怕的就是陷入永不结束的无穷递归中 , 所以, 每个递归定义 必须至少有一个条件,满足时递归不再进行,即不再引用自身而是返回值退出。 比如 刚才的伊j子,总有一次递归会使得 i<2 的,这样就可以执行 return i 的语句而不用继续递归了。
对比了两种实现斐波那契的代码。 选代和递归的区别是:迭代使用的是循环结构,递归使用的是选择结构。递归能使程序的结构更清晰、更简洁、更容易让人理 解,从而减少读懂代码的时间。但是大量的递归调用会建立函数的副本,会耗费大量 的时间和内存。选代则不需要反复调用函数和占用额外的内存。因此我们应该视不同 情况选择不同的代码实现方式。
那么我们讲了这么多递归的内容,和栈有什么关系呢?这得从计算机系统的内部 说起。
前面我们已经看到递归是如何执行它的前行和退回阶段的。递归过程退回的顺序它前行顺序的逆序。在退回过程中,可能要执行某些动作,包括恢复在前行过程中 存储起来的某些数据。
这种存储某些数据,并在后面又以存储的逆序恢复这些数据,以提供之后使用的 需求,显然很符合钱这样的数据结构,因此, 编译器使用植实现递归就没什么好惊讶的了。
简单的说,就是在前行阶段,对于每一层递归,函数的局部变量、参数值以及返 回地址都被压入栈中。在退回阶段,位于栈顶的局部变量、 参数值和返回地址被弹 出,用于返回调用层次中执行代码的其余部分,也就是’恢复了调用的状态。
当然,对于现在的高级语言,这样的递归问题是不需要用户来管理这个栈的 , 一切都由系统代劳了。
递归的应用场景
看个实际应用场景,迷宫问题(回溯), 递归(Recursion)
递归的概念
简单的说: 递归就是方法自己调用自己,每次调用时传入不同的变量.递归有助于编程者解决复杂的问题,同时可以让代码变得简洁。
递归的调用机制
我列举两个小案例,来帮助大家理解递归,部分学员已经学习过递归了,这里在给大家回顾一下递归调用机制
打印问题
阶乘问题
package com.zcr.recursion;
/**
* @author zcr
* @date 2019/7/6-18:01
*/
public class RecursionTest {
public static void main(String[] args) {
//通过打印问题,回顾递归调用机制
//test(5);
//阶乘问题
int res = factorial(3);
System.out.println(res);
}
//打印问题
public static void test(int n) {
if (n > 2) {
test(n -1);
}
System.out.println("n=" + n);
}
//阶乘问题
public static int factorial(int n) {
if (n == 1) {
return 1;
} else {
return factorial(n - 1)*n;//factorial(2-1)*2 //factorial(3-1)*3=factorial(2-1)*2*3
}
}
}
递归用于解决什么样的问题
各种数学问题如: 8皇后问题 , 汉诺塔, 阶乘问题, 迷宫问题, 球和篮子的问题(google编程大赛)
各种算法中也会使用到递归,比如快排,归并排序,二分查找,分治算法等.
将用栈解决的问题–>第归代码比较简洁
递归需要遵守的重要规则
1.执行一个方法时,就创建一个新的受保护的独立空间(栈空间)
2.方法的局部变量是独立的,不会相互影响, 比如n变量
3.如果方法中使用的是引用类型变量(比如数组),就会共享该引用类型的数据.
4.递归必须向退出递归的条件逼近,否则就是无限递归,出现StackOverflowError,死龟了:) 栈溢出的错误!
5.当一个方法执行完毕,或者遇到return,就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕。
迷宫问题
说明:
小球得到的路径,和程序员设置的找路策略有关即:找路的上下左右的顺序相关
再得到小球路径时,可以先使用(下右上左),再改成(上右下左),看看路径是不是有变化
测试回溯现象
思考: 如何求出最短路径?
思考: 如何求出最短路径? => 最简单的方法就是对上下左右的找路策略进行穷举,然后比较哪个最短即可.
package com.zcr.recursion;
/**
* @author zcr
* @date 2019/7/6-20:24
*/
public class MiGong {
public static void main(String[] args) {
//先创建一个二维数组模拟迷宫
//地图
int[][] map = new int[8][7];
//使用1表示墙
//上下全部置为1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
//左右全部置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//设置挡板
map[3][1] = 1;
map[3][2] = 1;
/* 测试回溯的用法
map[1][2] = 1;
map[2][2] = 1;*/
//输出地图
System.out.println("地图情况:");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
//使用递归回溯给小球找路
//setWay(map, 1, 1);
setWay2(map,1,1);
//输出新的地图,小球走过,并标识过的递归
System.out.println("小球走过,并标识过的地图情况:");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
//使用递归回溯来给小球找路
//说明
//1.map表示地图
//2.i,j表示从地图中哪个位置出发(1,1)
//3.如果小球能到map[6][5],则说明通路找到
//4.约定:当map[i][j]为0时,表示该点没有走过,为1时代表墙,为2时表示通路可以走,为3表示该位置已经走过但是走不通
//5.在走迷宫时,需要确定一个策略(方法) 先走下-》右-》上-》左,如果该点走不通,再回溯
/**
* @param map 表示地图
* @param i 表示从哪个位置开始找
* @param j
* @return 如果找到通路,返回true;否则返回false
*/
public static boolean setWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {
//通路已经找到
return true;
} else {
if (map[i][j] == 0) {
//如果当前这个点还没有走过
//按照策略走
//在走之前先把这个点置为2,假定该点是可以走通的
map[i][j] = 2;
if (setWay(map, i + 1, j)) {//向下走
return true;
} else if (setWay(map, i, j + 1)) {//向右走
return true;
} else if (setWay(map, i - 1, j)) {//向上走
return true;
} else if (setWay(map, i, j - 1)) {//向左走
return true;
} else {
//说明该点走不通,是死路
map[i][j] = 3;
return false;
}
} else {//如果map[i][j]!=0,可能是1,2,3
return false;
}
}
}
//修改找路的策略,改成上-》右-》下-》左
public static boolean setWay2(int[][] map, int i, int j) {
if (map[6][5] == 2) {
//通路已经找到
return true;
} else {
if (map[i][j] == 0) {
//如果当前这个点还没有走过
//按照策略走
//在走之前先把这个点置为2,假定该点是可以走通的
map[i][j] = 2;
if (setWay2(map, i - 1, j)) {//向上走
return true;
} else if (setWay2(map, i, j + 1)) {//向右走
return true;
} else if (setWay2(map, i + 1, j)) {//向下走
return true;
} else if (setWay2(map, i, j - 1)) {//向左走
return true;
} else {
//说明该点走不通,是死路
map[i][j] = 3;
return false;
}
} else {//如果map[i][j]!=0,可能是1,2,3
return false;
}
}
}
}
八皇后问题介绍
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即:任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
八皇后问题算法思路分析
1.第一个皇后先放第一行第一列
2.第二个皇后放在第二行第一列、然后判断是否OK, 如果不OK,继续放在第二列、第三列、依次把所有列都放完,找到一个合适
3.继续第三个皇后,还是第一列、第二列……直到第8个皇后也能放在一个不冲突的位置,算是找到了一个正确解
4.当得到一个正确解时,在栈回退到上一个栈时,就会开始回溯,即将第一个皇后,放到第一列的所有正确解,全部得到.
5。然后回头继续第一个皇后放第二列,后面继续循环执行 1,2,3,4的步骤 【示意图】
说明:理论上应该创建一个二维数组来表示棋盘,但是实际上可以通过算法,用一个一维数组即可解决问题.
arr[8] = {0 , 4, 7, 5, 2, 6, 1, 3} //对应arr 下标 表示第几行,即第几个皇后,arr[i] = val , val 表示第i+1个皇后,放在第i+1行的第val+1列
package com.zcr.recursion;
/**
* @author zcr
* @date 2019/7/6-21:40
*/
public class Queen8 {
//定义一个max表示共有多少个皇后
int max = 8;
//定义数组array,保存皇后放置位置的结果
int[] array = new int[max];
static int count = 0;
public static void main(String[] args) {
//测试一把,8皇后是否正确
Queen8 queen8 = new Queen8();
queen8.check(0);
System.out.println("一共有" + count + "种解");
}
//写一个方法,可以将皇后摆放的位置输出
public void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
//查看当我们放置第n个皇后时,就去检测该皇后是否和前面已经摆放的皇后冲突
/**
*
* @param n 表示第n个皇后
* @return
*/
public boolean judge(int n) {
for (int i = 0; i < n; i++) {
//1.array[i] == array[n]表示判断第n个皇后是否和前面的n-1个皇后在同一列
//2.Math.abs(n - i) == Math.abs(array[n] - array[i])表示判断第n个皇后是否和第i个皇后同一斜线
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
//放置第n个皇后
//特别注意:check是每一次递归时,进入到check中都有一个for循环,因此会有回溯
public void check(int n) {
if (n == max) {//n=8,其实8个皇后就已经放好了
print();
return;
}
//依次放入皇后并判断是否冲突
for (int i = 0; i < max; i++) {
//先把当前这个皇后n,放到该行的第1列
array[n] = i;
//判断当放置第n个皇后到i列时,是否冲突
if (judge(n)) {//不冲突
//接着放第n+1个皇后,即开始递归
check(n + 1);
}
//如果冲突,就继续执行array[n]=i,即将第n个皇后放置在本行后移的一个位置
}
}
}
4.9栈的应用——四则运算表达式求值 104
4.9.1后缀(逆波兰)表示法定义 104
栈的现实应用也很多,我们再来重点讲一个比较常见的应用:数学表达式的求值。
括号都是成对出现的,有左括号就一定会有右括号,对于多 重括号,最终也是完全嵌套匹配的。 这用栈结构正好合适,只有碰到左括号,就将此 左括号进枝,不管表达式有多少重括号,反正遇到左括号就进栈,而后面出现右括号 时,就让栈顶的左括号出栈, 期间让数字运算,这样,最终有括号的表达式从左到右 巡查一遍,栈应该是由空到有元素,最终再因全部匹配成功后成为空栈的结果。
但对于四则运算,括号也只是当中的一部分,先乘除后加减使得问题依然复杂, 如何有放地处理它们呢?我们伟大的科学家想到了好办法。
20 世纪 50 年代s 波兰逻辑学家 J8111 :tukasiewicz,当时也和我们现在的同学们一 样,困惑于如何才可以搞定这个四则运算,习之知道他是否也像牛顿被苹果砸到头而想 到万有引力的原理,或者还是阿基米德在浴缸中洗澡时想到判断皇冠是否纯金的办 法,总之他也是灵感突现,想到了一种不需要括号的后缀表达法,我们也把它称为逆波兰 (Reverse Polish Notation, RPN) 表示。 我想可能是他的名字太复杂了,所以 后人只用他的国籍而不是姓名来命名,实在可惜。这也告诉我们,想要流芳百世,名 字还要起得朗朗上口才行。这种后缀表示法,是表达式的一种新的显示方式,非常巧 妙地解决了程序实现四则运算的难题。
我们先来看看,对于"9+ (3-1) X3+10-:-2" ,如果要用后缀表示法应该是什么 样子: “93 1-3*+102/+” ,这样的表达式称为后缀表达式,叫后缀的原因在于所有的符号都是在要运算数字的后面出现。显然,这里没有了括号。对于从来没有接触 过后缀表达式的同学来讲,这样的表述是很难受的。不过你不喜欢,有机器喜吹,比 如我们聪明的计算机。
4.9.2后缀表达式计算结果 106
程序中解决四则运算是比较麻烦的,因为计算有优先级,波兰逻辑学家发明了一种不需要括号的后缀表达法,称为逆波兰表示
如
9 + (3 - 1) x 3 + 10 ÷ 2
转换成后缀表达式为
9 3 1 - 3 * + 10 2 / +
转换规则:
从左到右遍历表达式的每个数字和符号,若是数字就输出,即成为后缀表达式的一部分,若是符号,则判断其与栈顶符号的优先级,是右括号或优先级低于栈顶符号(乘除优先加减)则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止
计算规则:
从左到右遍历表达式的每个数字和符号,遇到是数字就进栈,遇到是符号,就将处于栈顶两个数字出栈,进行运算,运算结果进栈,一直到最终获得结果
后缀表达式计算结果
为了解释后缀表达式的好处,我们先来看看,计算机如何应用后缀表达式计算出 最终的结果 20 的。
后缀表达式: 931- 3*+102/ +
规则:从左到右遍历表达式的每个数字和符号,遇到是数字就进枝,遇到是符 号,就将处于桔顶两个数字出拢,进行运算,运算结果进钱, 一直到最终获得结果。
4.9.3中缀表达式转后缀表达式 108
我们把平时所用的标准四则运算表达式 ,即 “9+ (3-1) X3+10-;.-2” 叫做中级 表达式。因为所有的运算符号都在两数字的中阁,现在我们的问题就是中缀到后缀的 转化。
中缀表达式 “9+(3-1) X 3+10+2” 转化为后缀表达式 “931-3*+102/+”。
规则 : 从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后 缀表达式的一部分i 若是符号,则判断其与楼顶符号的优先级,是右括号或优先级低 于槐顶符号(乘除优先加减)则检顶元素依次出钱并输出 , 并将当前符号进梢,一直 到最终输出后缀表达式为止。
从刚才的推导中你会发现, 要想让计算机具有处理我们通常的标准(中缀)表达 式的能力,最重要的就是两步:
- 将中缀表达式转化为后缀表达式(栈用来迸出运算的符号)。
- 将后缀表达式进行运算得出结果(栈用来进出运算的数字)。
整个过程,都充分利用了栈的后进先出特性来处理,理解好它其实也就理解好了栈这个数据结构。
4.10队列的定义 111
电脑有时会处于疑似死机的状态。就当你失去耐心,打算了reset时。突然它像酒醒了一样,把你刚才点击的所有操作全部都按顺序执行了一遍。这其实是因为操作 系统中的多个程序因需要通过一个通道输出,而按先后次序排队等待造成的。
再比如像移动、联迪、电信等客服电话,客服人员与客户相比总是少数,在所有 的客服人员都占线的情况下,客户会被要求等待,直到有某个客服人员空下来,才能 让最先等待的客户接通电话。这里也是将所有当前拨打客服电话的客户进行了排队处理。
操作系统和客服系统中,都是应用了一种数据结构来实现刚才提到的先进先出的 排队功能,这就是队列。
队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表
队列是一种先进先出(First In First Out)的线性表,简称FIFO。允许插入的一 端称为队尾,允许删除的一端称为队头。
队列在程序设计中用得非常频繁。前面我们已经举了两个例子,再比如用键盘进 行各种字母或数字的输入,到显示器上如记事本软件上的输出,其实就是队列的典型应用,假如你本来和女友聊天,想表达你是我的上帝,输入的是 god,而屏幕上却显 示出了 由g 发了出去,这真是要气死人了。
队列是一个有序列表,可以用数组或是链表来实现。
因为队列的输出、输入是分别从前后端来处理,因此需要两个变量 front及 rear分别记录队列前后端的下标,front 会随着数据输出而改变,而 rear则是随着数据输入而改变
数组模拟队列
当我们将数据存入队列时称为”addQueue”,addQueue 的处理需要有两个步骤:思路分析
将尾指针往后移:rear+1 , 当front == rear 【空】
若尾指针 rear 小于队列的最大下标 maxSize-1,则将数据存入 rear所指的数组元素中,否则无法存入数据。 rear == maxSize - 1[队列满]
出队列操作getQueue
显示队列的情况showQueue
查看队列头元素headQueue
退出系统exit
package com.zcr.queue;
import java.util.Scanner;
/**
* @author zcr
* @date 2019/7/4-22:28
*/
public class ArrayQueueDemo {
public static void main(String[] args) {
//创建一个队列
ArrayQueue arrayQueue = new ArrayQueue(3);
char key = ' ';//接口用户输入
Scanner scanner = new Scanner(System.in);
boolean loop = true;
//输出一个菜单
while (loop) {
System.out.println("s(show):显示队列");
System.out.println("e(exit):退出程序");
System.out.println("a(add):添加数据到队列");
System.out.println("g(get):从队列中取出数据");
System.out.println("h(head):查看队列头的数据");
key = scanner.next().charAt(0);//接收一个字符
switch (key) {
case 's':
arrayQueue.showQueue();
break;
case 'a':
System.out.println("请输入一个数字");
int value = scanner.nextInt();
arrayQueue.addQueue(value);
break;
case 'g':
try {
int res = arrayQueue.getQueue();
System.out.printf("取出的数据是%d\n",res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case 'h':
try {
int res = arrayQueue.headQueue();
System.out.printf("队列头是%d\n",res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case 'e':
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("程序退出");
}
}
//使用数组模拟队列--编写一个ArrayQueue类
class ArrayQueue{
private int maxsize;//数组的最大容量
private int front;//队列头
private int rear;//队列尾
private int[] arr;//存放数组
//创建队列的构造器
public ArrayQueue(int maxsize) {
this.maxsize = maxsize;
arr = new int[maxsize];
front = -1;//指向队列头部,分析出指向队列头的前一个位置
rear = -1;//指向队列尾部,指向队列尾的数据(即就是队列最后一个数组)
}
//判断队列是否满
public boolean isFull() {
return rear ==maxsize - 1;
}
//判断队列是否为空
public boolean isEmpty() {
return rear == front;
}
//添加数据到队列
public void addQueue(int n) {
//判断队列是否满
if (isFull()) {
System.out.println("队列满,不能加入数据");
return;
}
rear++;//让rear后移
arr[rear] = n;
}
//获取队列的数据,数据出队列
public int getQueue() {
//判断队列是否空
if (isEmpty()) {
//System.out.println("队列空,不能");
//通过抛出异常来处理
throw new RuntimeException("队列空,不能取数据");
}
front++;//本身指向队列头的前一个位置,所以先让他后移一个位置,再取
return arr[front];
}
//显示队列的所有数据
public void showQueue() {
if (isEmpty()){
System.out.println("队列空,没有数据");
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.printf("arr[%d]=%d\n",i,arr[i]);
}
}
//显示队列的头数据是多少,注意不是取出数据
public int headQueue() {
if (isEmpty()){
//System.out.println("队列空,没有数据");
throw new RuntimeException("队列空,没有数据");
}
return arr[front+1];
}
}
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
s
队列空,没有数据
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
a
请输入一个数字
10
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
a
请输入一个数字
20
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
a
请输入一个数字
30
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
s
arr[0]=10
arr[1]=20
arr[2]=30
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
h
队列头是10
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
h
队列头是10
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
g
取出的数据是10
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
h
队列头是20
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
g
取出的数据是20
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
h
队列头是30
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
g
取出的数据是30
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
h
队列空,没有数据
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
g
队列空,不能取数据
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
g
队列空,不能取数据
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
h
队列空,没有数据
s(show):显示队列
e(exit):退出程序
a(add):添加数据到队列
g(get):从队列中取出数据
h(head):查看队列头的数据
数组模拟环形队列
对前面的数组模拟队列的优化,充分利用数组. 因此将数组看做是一个环形的。(通过取模的方式来实现即可)
分析说明:
尾索引的下一个为头索引时表示队列满,即将队列容量空出一个作为约定,这个在做判断队列满的
时候需要注意 (rear + 1) % maxSize == front 满]
rear == front [空]
package com.zcr.queue;
import java.util.Scanner;
/**
* @author zcr
* @date 2019/7/4-22:28
*/
public class CircleQueueDemo {
public static void main(String[] args) {
//创建一个环形队列
CircleQueue circleQueue = new CircleQueue(4);//有一个空的,所以这里有效空间为3
char key = ' ';//接口用户输入
Scanner scanner = new Scanner(System.in);
boolean loop = true;
//输出一个菜单
while (loop) {
System.out.println("s(show):显示队列");
System.out.println("e(exit):退出程序");
System.out.println("a(add):添加数据到队列");
System.out.println("g(get):从队列中取出数据");
System.out.println("h(head):查看队列头的数据");
key = scanner.next().charAt(0);//接收一个字符
switch (key) {
case 's':
circleQueue.showQueue();
break;
case 'a':
System.out.println("请输入一个数字");
int value = scanner.nextInt();
circleQueue.addQueue(value);
break;
case 'g':
try {
int res = circleQueue.getQueue();
System.out.printf("取出的数据是%d\n",res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case 'h':
try {
int res = circleQueue.headQueue();
System.out.printf("队列头是%d\n",res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case 'e':
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.println("程序退出");
}
}
//使用数组模拟队列--编写一个ArrayQueue类
class CircleQueue{
private int maxsize;//数组的最大容量
private int front;//队列头
private int rear;//队列尾
private int[] arr;//存放数组
//创建队列的构造器
public CircleQueue(int maxsize) {
this.maxsize = maxsize;
arr = new int[maxsize];
front = 0;//指向队列的第一个元素
rear = 0;//指向队列的最后一个的后一个位置。因为希望空出一个位置
}
//判断队列是否满
public boolean isFull() {
return (rear + 1) % maxsize == front;
}
//判断队列是否为空
public boolean isEmpty() {
return rear == front;
}
//添加数据到队列
public void addQueue(int n) {
//判断队列是否满
if (isFull()) {
System.out.println("队列满,不能加入数据");
return;
}
arr[rear] = n;//以为rear指的就是最后一个元素的后一个位置
rear = (rear + 1) % maxsize;//让rear后移
}
//获取队列的数据,数据出队列
public int getQueue() {
//判断队列是否空
if (isEmpty()) {
//System.out.println("队列空,不能");
//通过抛出异常来处理
throw new RuntimeException("队列空,不能取数据");
}
int value = arr[front]; //本身指向队列的第一个元素,所以直接返回后,再移动
front = (front + 1) % maxsize;
return value;
}
//显示队列的所有数据
public void showQueue() {
if (isEmpty()){
System.out.println("队列空,没有数据");
return;
}
//从front开始遍历,遍历多少个元素
//
for (int i = front; i < front + size(); i++) {
System.out.printf("arr[%d]=%d\n",i % maxsize,arr[i % maxsize]);
}
}
//求出当前队列有效数据的个数
public int size() {
return (rear + maxsize - front) % maxsize;
}
//显示队列的头数据是多少,注意不是取出数据
public int headQueue() {
if (isEmpty()){
//System.out.println("队列空,没有数据");
throw new RuntimeException("队列空,没有数据");
}
return arr[front];
}
}
测试示意图:
课堂练习:
同学们完成环形数组模拟的队列的输出
(cq.rear + cq.maxSize – cq.front) % cq.maxSize
4.11队列的抽象数据类型 112
同样是线性表,队列也有类似线性表的各种操作,不同的就是插入数据只能在队 尾进行,删除数据只能在队头进行。
4.12循环队列 113
你上了公交车发现前排有两个空座位,而后排所有座位都已经坐满,你会怎么做?立马下车,并对自己说,后面没座了,我等下一辆?没这么笨的人,前面有座位,当然也是可以坐的。
队列的头尾相接的顺序存储结构称为循环队列
线性表有顺序存储和链式存储,棋是线性衰,所以有这两种存储方式。同样,队 列作为一种特殊的钱性衰,也同样存在这两种存储方式。我们先来看队列的顺序存储结构。
4.12.1队列顺序存储的不足 112
我们假设一个队列有 n 个元素,则JI民序存储的队列需建立一个大于 n 的数组,并 把队列的所有元素存储在数组的前 n 个单元,数组下标为 0 的一端即是队头。所谓的 入队列操作,其实就是在队尾追加一个元素,不需要移动任何元素,因此时间复杂度为O(1)。
与栈不同的是,队列元素的出列是在队头,即下标为 0 的位置,那也就意味着, 队列中的所有元素都得向前移动,以保证队列的队头,也就是下标为 0 的位置不为 空,此时时间复杂度为 O(n)
这里的实现和线性表的顺序存储结构完全相同,不再详述。
在现实中也是如此, 一群人在排队买票,前面的人买好了离开, 后面的人就要全 部向前一步,补上空位,似乎这也没什么不好。
可有时想想,为什么出队列时一定要全部移动呢,如果不去限制队列的元素必须 存储在数组的前 n 个单元这一条件,出队的性能就会大大增加。 也就是说,队头不需 要一定在下标为 0 的位置
为了避免当只有一个元素时,队头和队尾重合使处理变得麻烦,所以引入两个指 针, front 指针指向队头元素 , rear 指针指向队尾元素的下一个位置,这样当 的front 等 于 rear 时,此队列不是还剩一个元素,而是空队列。
假设是长度为 5 的数组,初始状态,空队列如图 。 front 与 rear 指针均指向下标为 0 的位置。 然后入队 al、 a2、 a3、 a4, front 指针依然指向下标 为 0 位置,而 rear 指针指向下标为 4 的位置,如图
出队 al、 缸,则 front 指针指向下标为 2 的位置, rear 不变,如图 。再入队 as,此时 front 指针不变, rear 指针移动到数组之外。嗯?数组之外, 那将是哪里?如图
问题还不止于此。假设这个队列的总个数不超过 5 个,但目前如果接着人队的 话,因数组末尾元素已经占用,再向后加,就会产生数组越界的错误,可实际上,我 们的队列在下标为 0 和 1 的地方还是空闲的。 我们把这种现象叫做"假滥出"。
4.12.2循环队列定义 114
所以解决假溢出的办法就是后面满了 ,就再从头开始,也就是头尾相接的循环。 我们把队列的这种头尾相接的顺序存储结构称为循环队列。
rear 可以改为指向下标为 0 的位置,这样就不会 造成指针指向不明的问题了
接着人队衔,将它放置于下标为 0 处, rear 指针指向下标为 1 处,如图 。若再人队衍,则 rear 指针就与 front 指针重合,同时指向下标为 2 的位 置,如图 。
• 此时问题又出来了,我们刚才说,空队列时, front等于此rear,现在当队列满 时,也是front等于此rear,那么如何判断此时的队列究竟是空还是满呢?
• 办法一是设置一个标志变量 flag, 当 front== rear,且 flag= 0 时为队列空, 当 front== rear,且 flag= 1 时为队列满。
• 办法二是当队列空时,条件就是 from = rear,当队列满时,我们修改其条 件,保留一个元素空间。也就是说,队列满时,数组中还有一个空闲单元 ,我们就认为此队列已经满了。
我们重点来讨论第二种方法,由于 rear 可能比 front大,也可能比 front 小,所以 尽管它们只相差一个位.琶时就是满的情况,但也可能是相差整整一圈。 所以若队列的最大尺寸为 QueueSize,那么队列满的条件是 (rear+l) %QueueSlze==front (取 模 “%” 的目的就是为了整合 rear 与 front 大小为一个问题)。
front=0,而 rear=4, (4+1) %5 = 0,所以此时队 列满
front = 2 而 rear = 10 (1 + 1) %5 = 2 ,所以此时 队列也是满的
front=2 而 rear= 0 , (0+1) %5 = 1 , 1 != 2,所以 此时队列并没有满。
当 rear> front 时,此时队列的长度 为 rear一front。但当 rear < front 时,队列长度分为 两段, 一段是 QueueSize-front, 另一段是 o + rear,加在一起,队列长度为 rear-front + QueueSize。因此通用的计算队列长度公式为:
(rear- front + QueueSize) %QueueSize
有了这些讲解,现在实现循环队列的代码就不难了。
循环队列代码
/**
* <循环队列>
*
* 注意点:表长的表示、队列满的判断、front和rear的改变
*
* @author Lai
*
*/
public class SqQueue<E> {
private E[] data;
private int front;
private int rear;
private int maxSize;
private static final int DEFAULT_SIZE= 10;
/*
* 初始化
*/
public SqQueue(){
this(DEFAULT_SIZE);
}
public SqQueue(int maxSize){
data=(E[]) new Object[maxSize];
this.maxSize=maxSize;
front=0;
rear=0;
}
/*
* 求循环队列长度
*/
public int getLength() {
return (rear-front+maxSize)%maxSize;
}
/*
* 入队操作
*/
public void enQueue(E e) {
if((rear+1)%maxSize==front)
throw new RuntimeException("队列已满,无法入队!");
data[rear]=e;
rear=(rear+1)%maxSize;
//不是rear=rear+1,当rear在数组尾部时,后移一位会转到数组头部
}
/*
* 出队操作
*/
public E deQueue() {
if(rear==front)
throw new RuntimeException("队列为空!");
E e=data[front];
front=(front+1)%maxSize;
//不是front++,理由同rear
return e;
}
/*
* 打印操作
*/
public void printQueue() {
int k=front;
for(int i=0;i<getLength();i++) {
System.out.print(data[k]+" ");
k=(k+1)%maxSize;
}
System.out.println();
}
/*
* 测试代码
*/
public static void main(String[] args) {
SqQueue<String> aQueue=new SqQueue<>(5);
aQueue.enQueue("a");
aQueue.enQueue("b");
aQueue.enQueue("c");
aQueue.enQueue("d");
aQueue.printQueue();
System.out.println("-----");
aQueue.getLength();
aQueue.deQueue();
aQueue.deQueue();
aQueue.enQueue("e");
aQueue.printQueue();
}
}
结果
a b c d
c d e
从这一段讲解,大家应该发现,单是顺序存储,若不是循环队列,算法的时间性 能是不高的,但循环队列又面临着数组可能会溢出的问题,所以我们还需要研究一下不需要担心队列长度的链式存储结构。
4.13队列的链式存储结构及实现 117
队列的链式存储结构,就是线性表的单链表,只不过它只能尾进头出,我们把它简称为链队列。
为了操作上的方便,我们将队头指针指向链队列的头结点,而队尾指针指向终端结点,如图
空队列肘, front 和 rear 都指向头结点,如图
链队列的结构为:
public class LinkQueue<E> {
private QNode front,rear;
private int count;
class QNode{
E data;
QNode next;
public QNode(E data,QNode next) {
this.data=data;
this.next=next;
}
}
public LinkQueue() {
front=new QNode(null, null);
rear=front;
count=0;
}
4.13.1队列链式存储结构入队操作118
人队操作时,其实就是在链衰尾部插入结点,如图
4.13.2队列链式存储结构出队操作 119
出队操作时,就是头结点的后继结点出队,将头结点的后继改为宫后面的结点, 若链表除头结点外只剩一个元素时, 则需将 rear 指向头结点,如图
链队列的代码
/**
* 链队列
*
* 注意点:出队操作时,若队头是队尾(即队中仅有一个结点),则删除后要将rear指向头结点。
*
* @author Yongh
*
* @param <E>
*/
public class LinkQueue<E> {
private QNode front,rear;
private int count;
class QNode{
E data;
QNode next;
public QNode(E data,QNode next) {
this.data=data;
this.next=next;
}
}
public LinkQueue() {
front=new QNode(null, null);
rear=front;
count=0;
}
/*
* 入队操作
*/
public void enQueue(E e) {
QNode node=new QNode(e, null);
rear.next=node;
rear=node;
count++;
}
/*
* 出队操作
*/
public E deQueue() {
if(rear==front)
throw new RuntimeException("队列为空!");
QNode node=front.next;
E e=node.data;
front.next=node.next;
//若队头是队尾,则删除后要将rear指向头结点。
if(rear==node)
rear=front;
node=null;
count--;
//通过count来判断,可能更容易理解
//if(count==0)
// rear=front;
return e;
}
/*
* 获取队列长度
*/
public int getLength() {
return count;
}
/*
* 打印输出队列
*/
public void printQueue() {
if(count==0) {
System.out.println("空队列");
}else {
QNode node=front;
for(int i=0;i<count;i++) {
node=node.next;
System.out.print(node.data+" ");
}
System.out.println();
}
}
/*
* 测试代码
*/
public static void main(String[] args) {
LinkQueue<String> lQueue =new LinkQueue<>();
lQueue.printQueue();
lQueue.enQueue("A");
lQueue.enQueue("B");
lQueue.enQueue("c");
lQueue.enQueue("D");
lQueue.printQueue();<br>
lQueue.deQueue();
lQueue.deQueue();
lQueue.enQueue("E");
lQueue.printQueue();
}
}
结果
空队列
A B c D
c D E
循环队列和链队列的比较
比较
循环队列与链队列的时间复杂度都为O(1)
循环队列需要事先申请好空间,使用期间不释放,而对于链队列,每次申请和释放结点也会存在一些时间开销
对于空间上来说,循环队列必须有一个固定的长度,所以就有了存储元素个数和空间浪费的问题,而链队列不存在这个问题,尽管它需要一个指针域,会产生一些空间上的开销,但也可以接受。 所以在空间上,链队列更加灵 活。
在可以确定队列长度最大值的情况下,建议用循环队列,如果无法预估队列的长度时,则用链队列
4.14总结回顾 120
又到了总结回顾的时间。我们这一章讲的是楼和队列,官们都是特殊的线性衰, 只不过对插入和删除操作做了限制。
栈 (stack) 是限定仅在表尾进行插入和删除操作的线性袭。
队列 (queue) 是只允许在一端进行插入操作,而在另一端进行删除操作的线性
衰。
它们均可以用线性表的顺序存储结构来实现,但都存在着顺序存储的一些弊端。
因此它们各自有各自的技巧来解决这个问题。
对于栈来说,如果是两个相同数据类型的楼,则可以用数组的两端作栈底的方法 来让两个栈共享数据,这就可以最大化地利用数组的空间。
对于队列来说,为了避免数组插入和删除时需要移动数据,于是就引入了循环队 列 ,使得队头和队尾可以在数组中循环变化。解决了移动数据的时间损耗,使得本来 插入和删除是 O(n)的时间复杂度变成了 。(1)。
它们也都可以通过链式存储结构来实现,实现原则上与线性表基本相同如图 4-14-1 所示。
4.15结尾语 121
人生,需要有队列精神的体现。南极到北极,不过是南纬90度到北纬90度的队列,如果你中途犹豫,临时转向,也许你就只能和企鹅相伴永远。可事实上,无论哪个方向,只要你坚持到底,你都可以到达终点。
第5章串 123
串(string): 是由零个或多个字符串组成的有限序列, 又各叫字符串 .
5.1开场白 124
“枯眼望遥山隔水,往来曾见几心知?壶空怕酌一杯酒,笔下难成和韵诗。途路阻人离别久,讯音无雁寄回迟。孤灯夜守长寥寂,夫忆妻兮父忆儿。”……可再仔细一读发现,这首诗竟然可以倒过来读。
这种诗体叫做回文诗。宫是一种可以倒读或反复回旋阅读的诗体。刚才这首就是 正读是丈夫思念妻子,倒读是妻子思念丈夫的古诗。是不是感觉很奇妙呢?
5.2串的定义 124
我所提到的“over”、“end”、“lie”其实就是“lover”、“friend”、“believe”这些单词字符串的子串。
串(string)是由零个或多个字符组成的有限序列,又名叫字符串
一般记为 s= “ala2…… .an” (0;;;‘时 , 其中, s 是串的名称,用双引号(有些书中 也用单引号)括起来的字符序列是串的值,注意单引号不属于串的内容。 ai (1<=i<=n)可以是字母、 数字或其他字符, i 就是该字符在串中的位置。 串中的字符数目 n 称 为串的长度, 定义中谈到"有限"是指长度 n 是一个有限的数值。 零个字符的审称为 空串 (null string) , 它的长度为零,可以直接用两双引号 ".…’ 表示,也可以用希腊 字母 “φ” 来表示。所谓的序列,说明昂的相邻字符之间具有前驱和后继的关系。
空格串,是只包含空格的串。注意它与空串的区别,空格串是有内容有长度的, 而且可以不止一个空格。
子串与主串,串中任意个数的连续字符组成的子序列称为该串的子串,相应地, 包含子串的串称为主串。
子串在主串中的位置就是子串的第一个字符在主串中的序号。
5.3串的比较 126
串的比较是通过组成串的字符之间的编码来进行的,而字符的编码指的是字符在对应字符集中的序号(如ASCII值)
ASCII 编码,更准确一点, 由 7 位二进制数表 示一个字符,总共可以表示 128 个字符。后来发现一些特殊符号的出现, 128 个不够 用,于是扩展 ASCII 码由 8 位二进制数表示一个字符,总共可以表示 256 个字符,这 已经足够满足以英语为主的语言和特殊符号进行输入、存储、输出等操作的字符需要 了。
可是,单我们国家就有除汉族外的满、田、藏、蒙古、 维吾尔等多个少数民族文 字,换作全世界估计要有成百上千种语言与文字,显然这 256 个字符是不够的,因此 后来就有了 Unicode 编码, 比较常用的是由 16 位的二进制数表示一个字符,这样总 共就可以表示 216 个字符,约是 65 万多个字符,足够表示世界上所有语言的所有字 符了。当然,为了和 ASCII 码兼容, Unicode 的前 256 个字符与 ASCIl 码完全相同。
所以如果我们要在 C 语言中比较两个串是否相等,必须是它们串的长度以及它们 各个对应位置的字特都相等时,才算是相等。即给定两个串 s= “a1a2……an” , t= “b1b2……bm” ,当且仅当 n=m,且 al=bl, a2=b2,……, an=bm 时,我们认为 s=t。
那么对于两个串不相等时,如何判定它们的大小呢。我们这样定义:
5.4串的抽象数据类型 127
串的逻辑结构和线性表很相似,不同之处在于串针对的是字符集,也就是串中的 元素都是字符
因此,对于串的基本操作与线性表是有很大差别的.线性表更关注的是单个元素 的操作,比如查找一个元素,插入或删除一个元素,但串中更多的是查找子串位置、 得到指定位置子串、替换子串等操作。
我们来看一个操作 Index 的实现算法。
5.5串的存储结构 128
感情上发生了问题,为了向女友解释一下,我准备发一条短信,一共打了75个字。最后八个字是“我恨你是不可能的”,点发送。后来得知对方收到的,只有70个字,短信结尾是“……我恨你”。
串的存储结构与线性表相同,分为两种:串的顺序存储结构和串的链式存储结构
5.5.1串的顺序存储结构 129
串的顺序存储结构是用一组地址连续的存储单元来存储串中的字符序列,按照预定义的大小,为每个定义的串变量分配一个固定长度的存储区,一般是用定长数组来定义
既然是定长数组,就存在一个预定义的最大串长度, 一般可以将实际的串长度值 保存在数组的 0 下标位置3 有的书中也会定义存储在数组的最后一个下标位置。但也 有些编程语言不想这么干,觉得存个数字占个空间麻烦。它规定在串值后面加一个不 计入串长度的结束标记字符,比如气"\0"来表示串值的终结,这个时候,你要想知道此时的串长度,就需要遍历计算-下才知道了,其实这还是需要占用-个空间,何必 呢。
刚才讲的串的顺序存储方式其实是有问题的,因为字符晤的操作,比如两串的连 接 Concat、新串的插入 如lnsert, 以及字符串的替换 Replace) 都有可能使得串序列 的长度超过了数组的长度 MaxSize.
于是对于串的顺序存储,有一些变化,串值的存储空间可在程序执行过程中动态 分配而得。比如在计算机中存在一个自由存储区,叫做"堆"。这个堆可由 C 语言的 动态分配函数 malloc()和 free ()来管理。
5.5.2串的链式存储结构 131
串结构中的每个元素数据是一个字符,如果一个结点对应一个字符,就会存在很大的空间浪费,因此可以考虑一个结点存放多个字符,最后一个结点若是未被占满时,可以用”#”或其他非串值字符补全,如下图所示
每个结点存多少个字符会直接影响串处理的效率,需要根据实际情况做出选择
串的链式存储结构除了在连接串与串操作时有一定方便之外,总的来说不如顺序存储灵活,性能也不如顺序存储结构好
5.6朴素的模式匹配算法 131
子串的定位操作通常称做串的模式匹配
假设我们要从下面的主串 S="googoogle"中,找到 T="google"这个子串的位置。我 们通常需要下面的步骤。
简单的说,就是对主串的每一个字符作为子串开头,与要匹配的字符串进行匹 配。对主E但做大循环,每个字符开头做 T 的长度的小循环,直到匹配成功或全部遍历完成为止。
前面我们已经用串的其他操作实现了模式匹配的算法 Index。现在考虑不用串的其他操作,而是只用基本的数组来实现同样的算法。注意我们假设主串 S 和要匹配的子 串 T 的长度存在 S[O]与 T[O]中。 实现代码如下:
为主串和子串分别定义指针i,j。
(1)当 i 和 j 位置上的字母相同时,两个指针都指向下一个位置继续比较;
(2)当 i 和 j 位置上的字母不同时,i 退回上次匹配首位的下一位,j 则返回子串的首位。
/**
* 朴素的模式匹配算法
* 说明:下标从0开始,与书稍有不同,但原理一样
* @author Yongh
*
*/
public class BruteForce {
/*
* 返回子串t在主串s中第pos个字符后的位置。若不存在返回-1
*/
int index(String s,String t,int pos) {
int i=pos; //i为主串位置下标
int j=0; //j为子串位置下标
while(i<s.length()&&j<t.length()) {
if(s.charAt(i)==t.charAt(j)) {
i++;
j++; //i和j指向下一个位置继续比较
}else { /*重新匹配*/
i=i-j+1; //退回上次匹配首位的下一位
j=0; //返回子串的首位
}
}
if(j==t.length()) {
return i-j;
}else {
return -1;
}
}
public static void main(String[] args) {
BruteForce sample =new BruteForce();
int a= sample.index("goodgoogle", "google", 0);
System.out.println(a);
}
}
结果
4
分析一下, 最好的情况是什么?那就是一开始就区配成功,比如 “googlegood” 中去找 google ,时间复杂度为 0(1)。 稍差一些,如果像刚才例子中第二、 三、四位 一样,每次都是首字母就不匹配,那么对 T 串的循环就不必进行了,比如 “abccdffgoogle” 中去找 google。 那么时间复杂度为 O(n+m) , 其中 n 为主串长度, m 为要匹配的子串长度。根据等概率原则,平均是 (n+m) /2 次查找,时间复杂度为 O(n+m).
那么最坏的情况又是什么?就是每次不成功的匹配都发生在串 T 的最后一个字 符。举一个很极端的例子。主串为s=”00000000000000000000000000000000000000000000000001”,而要匹配的子串为t=”0000000001”,……,前者是有 49 个 “0” 和 1 个 “I " 的主串,后者是 9 个 “0” 和 1 个"1” 的子串。在匹配时,每次都得将t中字符循环到最后一位才发现,哦,原来它们是不匹配的。这样等于 T串需要在 S 串 的前 40 个位置都需要判断 10 次,并得出不匹配的结论
子串的定位操作通常称做串的模式匹配,如从主串S=”goodgoogle”中,找到子串T=”google”这个子串的位置,通常需要下面的步骤
主串S第一位开始匹配,匹配失败
主串S第二位开始匹配,匹配失败
主串S第三位开始匹配,匹配失败
主串S第四位开始匹配,匹配失败
主串S第五位开始匹配,S与T,6个字母全匹配,匹配成功
时间复杂度为O(n+m),其中n为主串长度,m为要匹配的子串长度
极端情况下,主串为S=”00000000000000000000000001”,子串为T=”0001”,在匹配时,每次都得将T中字符循环到最后一位才发现不匹配,此时的时间复杂度为O((n-m+1)*m)
5.7kmp模式匹配算法 135
很多年前我们的科学家觉得像这种有多个0和1重复字符的字符串,却需要挨个遍历的算法,是非常糟糕的事情。
5.7.1kmp模式匹配算法原理 135
5.7.2next数组值推导 139
看一些例子:
5.7.3kmp模式匹配算法实现 141
思路:
在上图的比较中,当 i 和 j 等于5时,两字符不匹配。在朴素匹配算法中,会令i=1,j=0,然后进行下一步比较;但是,我们其实已经知道了i=1到4的主串情况了,没有必要重复进行i=2到4的比较,且我们观察“ABCABB”的B前面的ABCAB,其前缀与后缀(黄色部分)相同,所以可以直接进行上图中的第三步比较(令 i 不变,令 j 从5变成2,继续进行比较)。这就是KMP模式匹配算法的大概思路。这当中的 j 从5跳转到了2,2通过一个函数next(5)求得,next(5)即代表j=5位置不匹配时要跳转的下一个进行比较的位置。
KMP模式匹配算法:
为主串和子串分别定义指针 i 和 j 。
(1)当 i 和 j 位置上的字母相同时,两个指针都指向下一个位置继续比较;
(2)当 i 和 j 位置上的字母不同时,i 不变,j 则返回到next[j]位置重新比较。(暂时先不管next[]的求法,只要记得定义有next[0]=-1)
(3)当 j 返回到下标为0时,若当 i 和 j 位置上的字母仍然不同,根据(2),有 j = next[0]=-1,这时只能令 i 和 j 都继续往后移一位进行比较 (同步骤(1))。
上述内容可结合下图说明:
(1)i 和 j 从下标为0开始比较,该位置两字母相同,i 和 j 往后移继续比较;
(2)一直比较到 i 和 j 等于5时,两字母不同, i 不变,j 返回到 next[j]的位置重新比较,该子串的next[5]=2,所以 j 返回到下标为2的位置继续与 i=5的主串字母比较。
(3)在下图情况下,当j=0时,两字母不同,子串只能与主串的下一个元素比较了(即i=1与j=0比较)。根据(2),会使 j=next[j]=next[0]=-1,所以现在的i=0,j=next[0]=-1了,要下一步比较的话两个指针都要加一。
根据上述说明可以写出如下代码(代码中的next[]暂时假设已知,之后会讲):
/*
* 返回子串t在主串s中第pos个字符后的位置(包含pos位置)。若不存在返回-1
*/
public int index_KMP(String s, String t, int pos) {
int i = pos; //主串的指针
int j = 0; //子串的指针
int[] next = getNext(t); //获取子串的next数组
while (i < s.length() && j < t.length()) {
if (j == -1 || s.charAt(i) == t.charAt(j)) {
// j==-1说明了子串首位也不匹配,它是由上一步j=next[0]=-1得到的。
i++;
j++;
} else {
j = next[j];
}
}
if (j == t.length())
return i - j;
return -1;
}
next[]的定义与求解
根据上述内容可知,next[j] 的含义为:当下标为 j 的元素在不匹配时,j 要跳转的下一个位置下标。
继续结合下图说明
当j=5时,元素不匹配,j跳转到next[5]=2的位置重新比较。
那为什么next[5]的值为2呢?即,为什么j=5不匹配时要跳转到2位置呢?
观察 ABCABB 这个字符串,下标为5的字符为B,它前面的字符 ABCAB 与主串完全相同,而ABCAB的前缀与后缀(黄色部分)相同,,所以前缀AB不用再进行比较了,直接比较C这个字符,即下标为2的字符,所以next[5]=2。
那么该如何求解跳转位置next[]呢?通过刚才的讨论,我们可以发现next[j]的值等于 j 位置前面字符串的相同前后缀的最大长度,上面例子就是等于AB的长度2。
next[]的公式如下:
公式说明:
1.在j=0时,0位置之前没有字符串,next[0]定义为-1 ;
2. 在 j 位置之前的字符串中,如果有出现前后缀相等的情况,令 j 变为相等部分的最大长度,即刚刚所说的相同前后缀的最大长度。如上述的ABCABB字符串中,j=5时,前面相等部分AB长度为2,所以next[5]=2;
3.其余情况下,next[j]=0。其他情况,没有出现字符的前后缀相等,相同前后缀的最大长度自然就是0。
那求解next[]的代码如何实现呢?以下是代码的分析过程:
1.定义两个指针 i=0 和 j=-1,分别指向前缀和后缀( j 值始终要比 i 值小),用于确定相同前后缀的最大长度;(因为 i 是后缀,所以我们求的都是 i+1位置的next值next[i+1])
2.根据定义有:next[0]=-1;
3.当前缀中 j 位置的字符和后缀中 i 位置的字符相等时,说明 i+1 位置的next值为 j+1 (因为 j+1 为相同前后缀的最大长度,可结合下面两种情况思考)(即next[i+1]=j+1 )
4.j==-1时,说明前缀没有与后缀相同的地方,最大长度为0,则 i+1 位置的next值只能为0,此时也可以表示为next[i+1]=j+1。
5.当 j 位置的字符和 i 位置的字符不相等时,说明前缀在第 j 个位置无法与后缀匹配,令 j 跳转到下一个匹配的位置,即 j= next[j] 。
以下是实现求解next[]的程序:
/* * 返回字符串的next数组 */ public int[] getNext(String str) {
int length = str.length();
int[] next = new int[length]; //别忘了初始化
int i = 0; //i为后缀的指针
int j = -1; //j为前缀的指针
next[0] = -1;
while (i < length - 1) { // 因为后面有next[i++],所以不是i<length
if (j == -1 || str.charAt(i) == str.charAt(j)) { // j == -1代表前后缀没有相等的部分,i+1位置的next值为0
next[++i] = ++j; //等于前缀的长度
} else {
j = next[j];
}
}
return next; }
KMP完整代码
结合next数组的求解和KMP算法,完整代码如下:
import java.util.Arrays;
/**
* KMP模式匹配算法
* 返回子串t在主串s中第pos个字符后的位置。若不存在返回-1 要注意i不变,只改变j
*
* @author Yongh
*
*/
public class KMP {
/*
* 返回字符串的next数组
*/
public int[] getNext(String str) {
int length = str.length();
int[] next = new int[length]; //别忘了初始化
int i = 0; //i为后缀的指针
int j = -1; //j为前缀的指针
next[0] = -1;
while (i < length - 1) { // 因为后面有next[i++],所以不是i<length
if (j == -1 || str.charAt(i) == str.charAt(j)) { // j == -1代表前后缀没有相等的部分,i+1位置的next值为0
next[++i] = ++j; //等于前缀的长度
} else {
j = next[j];
}
}
return next;
}
/*
* 返回子串t在主串s中第pos个字符后的位置(包含pos位置)。若不存在返回-1
*/
public int index_KMP(String s, String t, int pos) {
int i = pos; //主串的指针
int j = 0; //子串的指针
int[] next = getNext(t); //获取子串的next数组
while (i < s.length() && j < t.length()) {
if (j == -1 || s.charAt(i) == t.charAt(j)) {
// j==-1说明了子串首位也不匹配,它是由j=next[0]=-1得到的。
i++;
j++;
} else {
j = next[j];
}
}
if (j == t.length())
return i - j;
return -1;
}
public static void main(String[] args) {
KMP aKmp = new KMP();
System.out.println(Arrays.toString(aKmp.getNext("BBC")));
System.out.println(Arrays.toString(aKmp.getNext("ABDABC")));
System.out.println(Arrays.toString(aKmp.getNext("ababaaaba")));
System.out.println(aKmp.index_KMP("goodgoogle", "google", 0));
}
}
结果
[-1, 0, 1]
[-1, 0, 0, 0, 1, 2]
[-1, 0, 0, 1, 2, 3, 1, 1, 2]
4
5.7.4kmp模式匹配算法改进 142
对于如下字符串,j=3时,next[j]=1,根据next的定义,即当 j=3位置不匹配时,j跳转到1位置重新比较,但可以发现,j=2位置和j=1位置其实是同一个字母,没有必要重复比较。
举个例子,在KMP算法下的比较过程如下(按图依次进行):
因为有next[3]=1,所以会出现中间这个其实可以省略掉的过程。实际上我们是可以直接跳到j=0那一步进行比较的,这就需要修改next数组,我们把新的数组记为nextval数组。
中间那步可以省略是因为,j=3和 j=1位置上的字符是完全相同的,因此没有必要再进行比较了。因此只需要在原有的next程序中加上一个字符是否相等的判断,如果要跳转的nextval位置上的字符于当前字符相等,令当前字符的nextval值等于要跳转位置上的nextval值。
KMP模式匹配算法的改进程序如下:
import java.util.Arrays;
/**
* KMP模式匹配算法 的改进算法
* 返回子串t在主串s中第pos个字符后的位置。若不存在返回-1 要注意i不变,只改变j
*
* @author Yongh
*
*/
public class KMP2 {
/*
* 返回字符串的next数组
*/
public int[] getNextval(String str) {
int length = str.length();
int[] nextval = new int[length];
int i = 0; //i为后缀的指针
int j = -1; //j为前缀的指针
nextval[0] = -1;
while (i < length - 1) {
if (j == -1 || str.charAt(i) == str.charAt(j)) {
i++;
j++;
if(str.charAt(i)!=str.charAt(j)) { //多了一个字符是否相等的判断
nextval[i] = j; //等于前缀的长度
}else {
nextval[i]=nextval[j];
}
} else {
j = nextval[j];
}
}
return nextval;
}
/*
* 返回子串t在主串s中第pos个字符后的位置(包含pos位置)。若不存在返回-1
*/
public int index_KMP(String s, String t, int pos) {
int i = pos; //主串的指针
int j = 0; //子串的指针
int[] next = getNextval(t); //获取子串的next数组
while (i < s.length() && j < t.length()) {
if (j == -1 || s.charAt(i) == t.charAt(j)) {
// j==-1说明了子串首位也不匹配,它是由j=next[0]=-1得到的。
i++;
j++;
} else {
j = next[j];
}
}
if (j == t.length())
return i - j;
return -1;
}
public static void main(String[] args) {
KMP2 aKmp = new KMP2();
System.out.println(Arrays.toString(aKmp.getNextval("BBC")));
System.out.println(Arrays.toString(aKmp.getNextval("ABDABC")));
System.out.println(Arrays.toString(aKmp.getNextval("ababaaaba")));
System.out.println(aKmp.index_KMP("goodgoogle", "google", 0));
}
}
结果
[-1, -1, 1]
[-1, 0, 0, -1, 0, 2]
[-1, 0, -1, 0, -1, 3, 1, 0, -1]
4
改进的算法仅在第24到28行代码发生了改变。
图中这句话可以结合下表仔细体会。(要记得nextval[j]的含义:j位置的字符未匹配时要跳转的下一个位置)
附:
要记住上面的算法,一定要记住指针 i 和 j 代表的意义,j==-1的意义,以及next的意义。
(getNext()中前缀位置和后缀位置,index_KMP()中主串位置和子串位置),(前缀或子串的首个字符就无法匹配),(要跳转的下一个位置)
还有要注意的就是,i为后缀,我们求的是下一个位置的next值,即next[i+1]。
5.7.5nextval数组值推导 144
5.8总结回顾 146
这一章节我们主重点讲了"串n 这样的数据结构,串 (string) 是由零个或多个字符 组成的有限序列,又名叫字特串。 本质上,它是一种线性袤的扩展,但相对于线性表 关注一个个元素来说, 我们对串这种结掏更多的是关注宫子串的应用问题,如查找、 替换等操作。现在的高级语言都有针对串的函数可以调用。 我们在使用这些函数的时 候,同时也应该要理解它当中的原理,以便于在碰到复杂的问题时,可以更加灵活的 使用,比如 KMP 模式匹配算法的学习,就是更有效地去理解 in似 函数当中的实现细 节。多用心一点,说不定有一天,可以有以你的名字命名的算法流传于后世。
推荐阅读:
https://blog.csdn.net/buppt/article/details/78531384
www.ruanyifeng.com/blog/2013/05/Knuth–Morris–Pratt_algorithm.html
https://blog.csdn.net/v_july_v/article/details/7041827
5.9结尾语 146
《璇玑图》共八百四十字,纵横各二十九字,纵、横、斜、交互、正、反读或退一字、迭一字读均可成诗,诗有三、四、五、六、七言不等,目前有人统计可组成七千九百五十八首诗。听清楚哦,是7958首。