Bootstrap

C++---实用编程技巧记录（使用库函数/ lambda表达式求最小、大值，排序等）

C++---实用编程技巧记录

注：为了写出高质量的代码，一些简单的逻辑尽量用库函数去实现，减少代码量；

1. 求最小值/最大值

  • 普通vector 求最小值
std::vector<double>  x={0,2,3,7,4,1};
auto min_inter = std::min_element(x.begin(), x.end());
double min= *min_inter; // 值
int index = std::distance(x.begin(),min_inter); //索引
  • map或者vector 根据需要根据某一维度数值获得最大最小值
// 使用lambda表达式
std::vector<cv::Point2f> pts;
auto compare_x = [](const cv::Point2f &p0, const cv::Point2f &p1) -> bool {
    return (p0.x < p1.x);
};
auto min_inter = std::min_element(pts.begin(), pts.end(),compare_x);
cv::Point2f min= *min_inter; // 值
int index = std::distance(pts.begin(),min_inter); //索引

以上当然可以直接进行排序，使用 sort函数

2. 排序


std::vector<cv::Point2f> pts;
// 升序
auto sort_x = [](const cv::Point2f &p0, const cv::Point2f &p1) -> bool {
    return (p0.x < p1.x);
};
std::sort(pts.begin(), pts.end(), sort_x);

lambda表达式 简写版：

std::sort(pts.begin(), pts.end(), [](const cv::Point2f &p0, const cv::Point2f &p1) {return p0.x < p1.x;});

3. 均值

double mean_ms = std::accumulate(std::begin(all_times),
                                           std::end(all_times), 0.0) /
                           all_times.size();

4 lambda 与多线程

4.1 多线程（类函数）

买东西 ：

class MyClassTest() {
    bool Buy(std::string type, int money) {
        // do something
        for (int i = 0; i < 10; ++i) {
            std::cout << "now is buy : " << type << std::endl;
        }
        return true;
    }
    bool RunMultiBuy() {
        auto buy_thread_0 =
            std::make_shared<std::thread>(&MyClassTest::Buy, this, "book", 20);
        buy_thread_0->join();

        auto buy_thread_1 =
            std::make_shared<std::thread>(&MyClassTest::Buy, this, "pen", 10);
        buy_thread_1->join();
    }
}

4.2 多线程（使用lambda）

买东西 ：

class MyClassTest() {
    bool RunMultiBuy() {
    	// lambda 已获取 this
        auto buy = [this](std::string type, int money) {
            // do something
            for (int i = 0; i < 10; ++i) {
                std::cout << "now is buy : " << type << std::endl;
            }
            return true;
        };

        auto buy_thread_0 = std::make_shared<std::thread>(buy, "book", 20);
        buy_thread_0->join();

        auto buy_thread_1 = std::make_shared<std::thread>(buy, "pen", 10);
        buy_thread_1->join();
    }
}

5. 查找

map 根据value 查找 key

 const std::map<std::string, int> str_id_map = {
    {"jack", 23424}, {"tom", 12533}, {"hopo", 5496}};
    
 int id = 12533;
 std::string name = "";
 const auto& str_map = str_id_map;
 auto iter =
     std::find_if(str_map.begin(), str_map.end(),
                  [id](const auto& item) { return item.second == id; });

 if (iter != str_map.end()) {
     name = iter->first;
 }

6. 对数组根据某个值进行分段

  1. 包含对数据的打印
  2. 对分段使用库函数处理
#include <algorithm>
#include <iostream>
#include <vector>

template <typename T>
std::ostream &operator<<(std::ostream &out, const std::vector<T> &ve) {
    out << "[";
    std::string delimiter = "\0";
    for (auto &item : ve) {
        out << delimiter << item;
        delimiter = ",";
    }
    out << "]\n";
    return out;
}
int main() {
    std::vector<int> points{1, 2, 3, 6};
    int cut_x = 6;
    auto iter =
        std::find_if(points.begin(), points.end(),
                     [&cut_x](const auto &val) { return val >= cut_x; });

    std::vector<int> points_1, points_2;
    if (iter == points.begin()) {
        points_2 = points;
    } else if (iter == points.end() || std::next(iter) == points.end()) {
        points_1 = points;

    } else {
        if (cut_x == (*iter)) {
            points_1.insert(points_1.end(), points.begin(), iter + 1);
            points_2.insert(points_2.end(), iter, points.end());
        }
        std::cout << *iter << std::endl;
    }
    std::cout << points_1;
    std::cout << points_2;
}

7. 查找

优雅的实现查找，在很多场景可以复用其中查找功能

#include <algorithm>
#include <iostream>
#include <memory>
#include <vector>

#define DEFINE_SMART_PTR(...) \
    DEFINE_PTR(__VA_ARGS__)   \
    DEFINE_UNIQUE_PTR(__VA_ARGS__)

#define DEFINE_PTR(...)                       \
    using Ptr = std::shared_ptr<__VA_ARGS__>; \
    using ConstPtr = std::shared_ptr<const __VA_ARGS__>;

#define DEFINE_CONTAINER(...)                                           \
    using CVector = std::vector<__VA_ARGS__::ConstPtr>;                 \
    using Vector = std::vector<__VA_ARGS__::Ptr>;                       \
    using CTable = std::unordered_map<uint64_t, __VA_ARGS__::ConstPtr>; \
    using Table = std::unordered_map<uint64_t, __VA_ARGS__::Ptr>;
    
#define DEFINE_UNIQUE_PTR(...)                      \
    using UniquePtr = std::unique_ptr<__VA_ARGS__>; \
    using ConstUniquePtr = std::unique_ptr<const __VA_ARGS__>;

template <typename T>
std::ostream &operator<<(std::ostream &out, const std::vector<T> &ve) {
    out << "[";
    std::string delimiter = "\0";
    for (auto &item : ve) {
        out << delimiter << item;
        delimiter = ",";
    }
    out << "]\n";
    return out;
}

class LaneLine {
 public:
    DEFINE_SMART_PTR(LaneLine)

    LaneLine() = default;

    id_t GetId() const { return id_; }
    void SetId(id_t id) { id_ = id; }

    std::vector<int> GetPts() const { return pts_; }
    void SetPts(std::vector<int> pts) { pts_ = pts; }

 private:
    std::vector<int> pts_;
    id_t id_;
};

int main() {
    auto new_line = std::make_shared<LaneLine>();
    std::vector<int> vec{1, 2, 3};
    new_line->SetId(1);
    new_line->SetPts(vec);

    auto new_line2 = std::make_shared<LaneLine>();
    std::vector<int> vec2{7, 8, 9};
    new_line2->SetId(2);
    new_line2->SetPts(vec2);

    std::vector<LaneLine::Ptr> lines{new_line, new_line2};

    auto findLine = [](const std::vector<LaneLine::Ptr> &lines, id_t id,
                       id_t *index) -> bool {
        auto iter = std::find_if(
            lines.begin(), lines.end(),
            [id](const auto &line) { return line->GetId() == id; });
        if (iter == lines.end()) return false;

        *index = std::distance(lines.begin(), iter);
        return true;
    };

    std::vector<id_t> line_ids = std::vector<id_t>({1, 2, 3});
    for (const auto &id : line_ids) {
        id_t index = 0;
        if (findLine(lines, id, &index) == true) {
            const auto &line = lines.at(index);
            std::cout << "fine line id: " << line->GetId()
                      << ", values: " << line->GetPts();
        }
    }
}

5 坐标转换与transform

将朝x轴方向的点集，转为朝z轴方向 （将朝前改为朝天上），有如下特点

  • 定义Point3D_t数据结构，并重载基本运算符，便于简单运算
  • 重载矩阵相乘，便于坐标转换
  • 分别使用旋转向量+旋转角度，欧拉角表示旋转矩阵
  • 使用三种方式利用 std::transform 库函数进行转换
#include <algorithm>
#include <iostream>
#include <memory>
#include <vector>

#include <Eigen/Core>
#include <Eigen/Geometry>

#include <sophus/se3.hpp>
#include <sophus/so3.hpp>
// #include <Sophus/se3.h>
// #include <Sophus/so3.h>

#include <Eigen/Dense>

#include <opencv2/core/core.hpp>

template <typename T>
std::ostream &operator<<(std::ostream &out, const std::vector<T> &ve) {
    out << "[";
    std::string delimiter = "\0";
    for (auto &item : ve) {
        out << delimiter << item;
        delimiter = ",";
    }
    out << "]\n";
    return out;
}

typedef float float32_t;
typedef double float64_t;
typedef long double float128_t;

template <typename T>
bool FloatEqual(const T x, const T y) {
    const T max_val = std::max({1.0, std::fabs(x), std::fabs(y)});
    return std::fabs(x - y) <= std::numeric_limits<T>::epsilon() * max_val;
}

// typedef Sophus::SE3d SE3;
// typedef Sophus::SO3d SO3;
struct Point3D_t {
    float64_t x = 0.0;
    float64_t y = 0.0;
    float64_t z = 0.0;
    float32_t weight = 1.0;
    Point3D_t() = default;
    Point3D_t(float64_t _x, float64_t _y) : x(_x), y(_y) {}
    Point3D_t(float64_t _x, float64_t _y, float64_t _z, float32_t _weight = 1.0)
        : x(_x), y(_y), z(_z), weight(_weight) {}

    Point3D_t operator-() const {
        Point3D_t p;
        p.x = -this->x;
        p.y = -this->y;
        p.z = -this->z;
        return p;
    }

    Point3D_t operator+(const Point3D_t &b) const {
        Point3D_t c;
        c.x = this->x + b.x;
        c.y = this->y + b.y;
        c.z = this->z + b.z;
        return c;
    }

    Point3D_t operator-(const Point3D_t &b) const {
        Point3D_t c;
        c.x = this->x - b.x;
        c.y = this->y - b.y;
        c.z = this->z - b.z;
        return c;
    }

    template <typename N,
              std::enable_if_t<std::is_arithmetic<N>::value, int> = 0>
    Point3D_t operator*(const N scalar) const {
        Point3D_t q;
        q.x = this->x * scalar;
        q.y = this->y * scalar;
        q.z = this->z * scalar;
        return q;
    }

    template <typename N,
              std::enable_if_t<std::is_arithmetic<N>::value, int> = 0>
    Point3D_t operator/(const N scalar) {
        Point3D_t c;
        c.x = this->x / scalar;
        c.y = this->y / scalar;
        c.z = this->z / scalar;
        return c;
    }

    bool operator==(const Point3D_t &b) const {
        return FloatEqual(this->x, b.x) && FloatEqual(this->y, b.y) &&
               FloatEqual(this->z, b.z);
    }

    bool operator!=(const Point3D_t &b) const {
        return !FloatEqual(this->x, b.x) || !FloatEqual(this->y, b.y) ||
               !FloatEqual(this->z, b.z);
    }

    friend std::ostream &operator<<(std::ostream &out, const Point3D_t &point) {
        out << "(" << point.x << ", " << point.y << ", " << point.z << ")";
        return out;
    }
};

template <typename D>
Point3D_t operator+(const Point3D_t &a, const Eigen::Matrix<D, 3, 1> &b) {
    Point3D_t c;
    c.x = a.x + b(0, 0);
    c.y = a.y + b(1, 0);
    c.z = a.z + b(2, 0);
    return c;
}

template <typename D>
Point3D_t operator*(const Eigen::Matrix<D, 3, 3> &R, const Point3D_t &q) {
    Point3D_t r(0, 0, 0);
    r.x = R(0, 0) * q.x + R(0, 1) * q.y + R(0, 2) * q.z;
    r.y = R(1, 0) * q.x + R(1, 1) * q.y + R(1, 2) * q.z;
    r.z = R(2, 0) * q.x + R(2, 1) * q.y + R(2, 2) * q.z;
    return r;
}

template <typename D>
Point3D_t operator*(const Eigen::Matrix<D, 4, 4> &T, const Point3D_t &q) {
    Point3D_t r(0, 0, 0);
    r.x = T(0, 0) * q.x + T(0, 1) * q.y + T(0, 2) * q.z + T(0, 3);
    r.y = T(1, 0) * q.x + T(1, 1) * q.y + T(1, 2) * q.z + T(1, 3);
    r.z = T(2, 0) * q.x + T(2, 1) * q.y + T(2, 2) * q.z + T(2, 3);
    return r;
}

inline Point3D_t operator*(const Sophus::SE3d &T, const Point3D_t &p) {
    return T.so3().matrix() * p + Point3D_t(T.translation().x(),
                                            T.translation().y(),
                                            T.translation().z());
}

inline Point3D_t operator*(const Sophus::SO3d &R, const Point3D_t &p) {
    return R.matrix() * p;
}

Eigen::Matrix3d ypr2R(const Eigen::Vector3d &ypr) {
    double y = ypr(0);
    double p = ypr(1);
    double r = ypr(2);

    Eigen::Matrix<double, 3, 3> Rz;
    Rz << cos(y), -sin(y), 0, sin(y), cos(y), 0, 0, 0, 1;

    Eigen::Matrix<double, 3, 3> Ry;
    Ry << cos(p), 0., sin(p), 0., 1., 0., -sin(p), 0., cos(p);

    Eigen::Matrix<double, 3, 3> Rx;
    Rx << 1., 0., 0., 0., cos(r), -sin(r), 0., sin(r), cos(r);

    return Rz * Ry * Rx;
}

int main() {
    // 前左上坐标系（x轴朝前）
    const std::vector<Point3D_t> pts{Point3D_t(1, 1, 0), Point3D_t(5, 1, 0)};

    // 将朝x轴方向的 点集，转为朝z轴
    // 定义旋转矩阵: 旋转角度+旋转向量，即绕（0,1,0）方向转90度
    Eigen::Matrix3d to_up =
        Eigen::AngleAxisd(-90.0 * M_PI / 180.0, Eigen::Vector3d(0, 1, 0))
            .toRotationMatrix();

    // 定义旋转矩阵: 欧拉角转为旋转矩阵
    // (将前左上的坐标系，变为下右前坐标系，这样原先在x轴朝向的点 会变为
    // z轴朝向)
    Eigen::Vector3d ypr;
    ypr << 0.0, -90.0 * M_PI / 180.0, 0.0;  // ypr(zyx)
    Eigen::Matrix3d to_up2 = ypr2R(ypr);
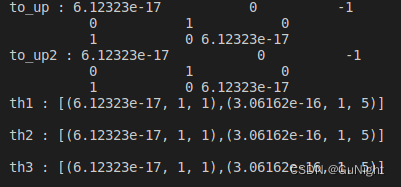
    std::cout << "to_up : " << to_up << std::endl;
    std::cout << "to_up2 : " << to_up2 << std::endl;

    {
        // 第1种转换
        // 改变输入数据值，构建lambda函数
        std::vector<Point3D_t> input_pts = pts;
        auto Transform = [&](std::vector<Point3D_t> *geometry) {
            std::transform(geometry->begin(), geometry->end(),
                           geometry->begin(),
                           [&](const Point3D_t &pt) { return to_up * pt; });
        };
        Transform(&input_pts);
        std::cout << "th1 : " << input_pts << std::endl;
    }
    {
        // 第2种转换
        // 改变输入数据值
        std::vector<Point3D_t> input_pts = pts;
        std::transform(input_pts.begin(), input_pts.end(), input_pts.begin(),
                       [&](const Point3D_t &pt) { return to_up * pt; });
        std::cout << "th2 : " << input_pts << std::endl;
    }
    {
        // 第3种转换
        // 不改变输入数据值
        std::vector<Point3D_t> pts_out;
        std::transform(pts.begin(), pts.end(), std::back_inserter(pts_out),
                       [&](const Point3D_t &pt) { return to_up2 * pt; });

        std::cout << "th3 : " << pts_out << std::endl;
    }
}

在这里插入图片描述

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
【嵌入式09】STM32串口通信，发送Hello Windows示例
Javascript中数组转成string
AI期末复习(PolyU)
vc6 使用的那些事
Ubuntu环境安装RabbitMQ
【JVM】面试篇
【自动驾驶】《无人驾驶原理与实践》源码教程（二）——NDT算法实例
jdk 配置环境变量
oracle数据库--练习题
Wireshark数据抓包分析之传输层协议（TCP协议）
;